Тұтас денедегі температуралық өрістің қалыптасуына жылу өткізбейтін қабаттың әсерін зерттеу

МАЗМҰНЫ

КIРIСПЕ

Табиғатта жүріп жататын процестердің ішіндегі ең күрделісінің бірі - жылу алмасу процесі. Ғылымда жылу алмасу процесі математикалық физика есептерінде қарастырылады. Процесс екінші ретті, дербес туындылы дифференциалдық теңдеумен сипатталады. Теңдеудің бос мүшесінің түріне байланысты Лаплас, немесе Пуассон теңдеуі деп аталатын бұл дифференциалдық теңдеулерді шекаралық шарттармен бірге шешу арқылы зерттеу аймағындағы температуралық өріс анықталады.

Дипломдық жұмыста зерттеу аймағы ретінде құрамында жер асты жылу тарату жүйесі бар қала іші автомобиль жолының құрылымы қарастырылған.

Қазіргі заманда ешбір кала, елді мекен жер асты коммуникациялық құрылымдарсыз толық қанды өмір сүре алмайтыны белгілі.

Жер асты коммуникациялары арқылы қала халқы жылумен, сумен, электр энергиясымен, байланыс жүйелерімен және т. б қамтамасыз етіледі. Бірақ, жер асты инженерлік жүйелерінің қала жолдарын пайдалану мен жөндеу кезінде тудыратын қиындықтары мол. Әдетте, жер асты коммуникациялық жүйелерін мүмкіндігінше көлік жүретін қатардан алыстау, тротуарлар мен жол жиегіндегі көгеріштердің астымен өткізуге тырысады. Бірақ, тарихи қалыптасқан дәстүр бойынша, ескі қалаларда, әсіресе, оңтүстік өңірдің қалаларында, жер тапшылығына байланысты қала жолдарының жалпақтығы жеткіліксіз болады да, жер асты инженерлік жүйелері автомобиль жолдарының тікелей астымен жүргізіледі. Нәтижесінде, жер асты коммуникациялық жүйелерінің кері әсерінен қала жолдары уақытынан бұрын істен шығып, жөндеу жұмыстарына қосымша қаржы мен уақыт қажет етеді. Аталған кері әсерлі жүйелердің ішінен жылу тарату жүйелерін ерекше бөліп қарастыруға болады. Ірі қалаларда жол жөндеуге жауапты мекеме қызметкерлері жер асты жылу жүйесінің жол бойының қай жерінде жатқанын жол төсемесінде пайда болған жарықшақтар арқылы ешбір қатесіз таба алады. Олардың пікірінше, жарықшақтардың пайда болуына бірінші себеп жылу тарату жүйелерінен бөлінетін жылу мөлшері. Жылу тарату жүйесінен бөлінетін жылу қыстың суық күндерінде асфальт төсемелердің астында ылғалды мол жинаған борпылдақ қабаттың пайда болуына себеп болады да, нәтижесінде жарықшақтар пайда болады. Жарықшақтар арқылы өткен су жол төсемесінің астының беріктігін одан арман төмендетіп жібереді.

Дипломдық жұмыстың мақсаты қала іші көпқабатты жол құрылымының температуралық күйінің жол қабаттарының жылуөткізгіштік қабілетіне байланысты өзгеру заңдылықтарын зерттеу.

Қойылған мақсатты орындау үшiн мынадай жұмыстар атқарылуы керек:

- қала іші жолдарының көлденең қималары үшiн есептеу схемалары мен есептеу алгоритмдерiн жасау және есептеу алгоритмдерiн компьютер арқылы жүзеге асыру;

- теориялық есептеулер арқылы жол құрылымында пайда болатын температуралық өрістің өзгеру заңдылықтарын анықтау;

- жүргiзiлген зерттеулердiң нәтижелерi негiзiнде жол конструкцияларындағы температуралық өрістің ерекшеліктерін жолдарды жобалау кезiнде ескерудiң тәсiлдерi туралы ұсыныстар жасау.

Дипломдық жұмыс кiрiспеден, үш бөлімнен тұратын негiзгi бөлiктен, қорытындыдан және пайдаланған әдебиеттер тiзiмiнен тұрады.

Бiрiншi бөлімде шекті элементтер әдісін компьютерде жүзеге асыруда қолданылатын MATLAB жүйесіне шолу жасалынады. MATLAB жүйесінің өзіндік алгоримдік тілінің құрылымына, оның мүмкіндіктеріне сараптама жасалынған. Бөлімнің екінші жартысында автомобиль жолдарының төсемелерiнiң температуралық күйінің өзгеру заңдылықтарын шекті элементтер әдісімен анықтаудың теориялық негіздері келтірілген. Математикалық физика теңдеулері пәнінде қарастырылатын тұтас денедегі температуралық өрістің негізгі теңдеуі келтіріледі, аталған әдістің негізгі теңдеулер жүйесін құру алгоритмы келтіріледі, және оны шешудің жолдары сарапталынады. Теңдеуді шешуге қажетті бастапқы және шекаралық шарттардың түрлері талқыланады.

Екінші бөлімде қала іші автомобиль жолдарының көпқабатты құрылымының температуралық күйін зерттеу есебі қойылған. Құрамында жер асты жылу тарату жүйесін қоршаған темір бетон коллектор бар автомобиль жолдарының көлденең қимасының эскизі келтіріліп, ондағы шекаралық шарттар температуралар арқылы және олардың конвективті түрде алмасу заңдылықтары арқылы берілген. Қала жолдарының көп қабатты болатыны ескеріліп, жол қабаттарының материалдарының геометриялық өлшемдері мен жылу-техникалық сипаттамалары келтірілген. Тереңдігі 10 м болатын горизонтал қабатта температура тұрақты деп алынып, зертеу аймағының екі вертикал қабырғаларында температура сызықтық заңдылықпен өзгереді деп қабылданған. Соңғы, үшінші бөлімде компьютерде есептелінген жол қимасындағы температуралық күйді зерттеу нәтижелері графикалық әдіспен келтірілген. Жол қабаттарының жылуөткізгіштік қасиеттерінің температуралық өріске әсерін зерттеу үшін жол төсемесінің астымен жүргізілген изоляциялық қабат енгізіліп, есептеу нәтижесі негізгі нұсқа нәтижесімен салыстырылған. Жылуөткізгіштіктің негізгі теңдеуі итерациялық, жоғарғы релакциялық Зейдель тәсілімен шешілген және нәтижесі изотермалар түрінде берілген. Алынған сандық нәтижені талдауға ыңғайлы болу үшін DELPHI тілінде арнайы “Изолиниялар” деп аталатын программа құрылған. Осы программаның көмегімен сандық нәтижелер тең деңгейлі сызықтар түрінде (изотермалар) көрсетілген.

Дипломдық жұмыс аумағында мынадай нәтижелер алынған:

• көп қабатты қала жолдарында пайда болатын жоласты жылу тарату жүйелерінің әсерінен пайда болатын қосымша температуралық өрісті анықтау мақсатында математикалық модель құрылған;
• аталған математикалық модельді жүзеге асыру үшін шекті элементтер әдісі қолданылып, есептеу программасы құрылған;

• есептік тәжiрибелер негiзiнде жол қабаттарының жылу өткізгіштік қасиеттері өзгертіліп, алынған нәтижелер салыстырылған.

1 САНДЫҚ ӘДІСТЕРДІ КОМПЬЮТЕРДЕ ЖҮЗЕГЕ АСЫРУДЫҢ

ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

1. МАТЕМАТИКАЛЫҚ ФИЗИКА ЕСЕПТЕРІН САНДЫҚ

ӘДІСПЕН ШЕШУДЕ ҚОЛДАНЫЛАТЫН MATLAB ЖҮЙЕСІНЕ

ҚЫСҚАША ШОЛУ

Жоғарғы деңгейлі программалау жүйелерінің ішіндегі қолданбалы математика саласында соңғы кезде жиі қолданылып жүрген жүйенің бірі - MATLAB [1-6] программалау жүйесі. MATLAB - матрицалық лаборатория - ғылыми-техникалық есептеулерге арналған ең үздік программалау жүйесінің бірі. Бұл жүйе қазіргі таңда есептеу математикасына, мәліметтерді өңдеуге, электрондық приборларды жобалауға, экономикаға және т. б. қолданбалы ғылым салаларына арналған бірнеше ондаған қосымшалармен толықтырылған.

MATLAB ең алдымен сандық алгоритмдерді программалауға арналған жүйе. Ол 1970 жылдары АҚШ-та жасалған қолданбалы LINPACK және EISPACK пакеттерінің негізінде пайда болды. MATLAB-тың пайда болуы қазіргі таңда үздік дамыған MathCad, MAPLE және Mathematica жүйелерінің өмірге келуіне себеп болды. MATLAB жүйесінің дамуына есептеу математикасының дамуы мен жеке компьютерлердің архитектурасының өзгерулері көп ықпал етті.

MATLAB - жоғары деңгейдегі программалау жүйесі. Оның құрамында барлық есептеулер түрлерін жүргізуге, мәліметтер қорымен жұмыс істеуге және ақпараттарды графикалық түрде өңдеуге арналған командалардың бай қоры бар. Бұл командалар MATLAB жүйесінің әртүрлі директорияларында орналасқан тақырыптық топтарға бөлінеді. Жүйеде 800-ге жуық командалар бар, олардың тең жартысына жуығы жүйемен жаңа танысып отырған қолданушыға түсінікті. Мүмкіндігі кеңірек командалар С тілінде жазылған. Бірақ, командалардың басым көпшілігі MATLAB жүйесінің тілінде. Сондықтан бұл жүйе қолданушы үшін әрқашан ашық. Жүйеде екі-, және үш өлшемді графиктермен жұмыс істеуге және жүйеде бар командаларды қолданып өз командаларын құруға зор мүмкіншілік бар. Сонымен қатар, С және Фортран тілінде жазылған программаларды MATLAB жүйесінде қолдануға болады.

Бұл жерде келтіріліп отырған мәліметтер жүйемен жаңадан танысуға және MATLAB жүйесінің мүмкіндіктерін зерттеуге арналған.

MATLAB жүйесін РС-де немесе Мас-та іске қосу үшін MATLAB-тың фирмалық суретін екі рет шертсе болғаны. MATLAB-ты UNIX жүйесінде іске қосу үшін операциялық жүйенің жұмыс терезесіндегі командалық қатарда matlab сөзін теру керек. MATLAB-тан шығу үшін командалар қатарында quit сөзін тереді.

MATLAB жүйесін игерудің ең оңай жолы - ол матрицалармен жұмыс істеуді үйрену. Себебі, MATLAB жүйесінің басқа жүйелерден негізгі ерекшелігі, бұл жүйеде барлық сандар әртүрлі реттегі матрицалар деп

қарастырылады. Мысалы, тұрақты сан (1 1) өлшемді матрица деп, ал вектор бір бағанадан немесе бір қатардан тұратын матрица деп қарастырылады. Жалпы түрдегі матрица деп төртбұрышты сандар массивын алады. Жүйенің тағы бір ерекшелігі, басқа жүйелерде матрицаны сандар жинағы деп қарастыратын болса, мұнда матрицаларға жеке сан ретінде қарап, оларға арифметикалық операциялардың барлық түрлерін сан ретінде қолдана береді. Осы айтылғандарды ескеріп MATLAB жүйесінде қолданылатын операцияларды матрицалары енгізуден бастайық.

Матрицаны енгізудің бірнеше тәсілі бар:

• элементтердің толық тізімін беру;
• матрицаны сыртқы файлдардан көшіріп алу;
• жүйеде бар арнайы функциялар арқылы матрицаны есептеп шығу;
• өзіңіз құрған М-файлдағы функция арқылы матрицаны есептеп шығу.

Матрицаны тізіммен енгізу үшін мынадай негізгі ережелерді ұстану керек:

• элементтер өзара бос орын немесе үтір арқылы бөлінеді;
• әрбір қатардың соңы нүкте-үтірмен (; ) белгіленеді;
• матрицаның барлық элементтері квадрат жақшамен ( [ ] ) қоршалады.

Енді MATLAB-та қолданылатын индекстермен танысайық. Матрицаның қатары i индексімен, бағанасы j индексімен жабдықталады да A(i, j) арқылы белгіленеді. Мысалы сиқырлы матрицаның төртінші бағанасының элементтерін есептеу үшін

A(1, 4) +A(2, 4) +A(3, 4) +A(4, 4)

командасын қолданып

ans=

34

мәнін аламыз. Бірақ бұл тәсіл тиімді емес. Мұндай жағдайда матрицаның бір ғана индексін өзгерту тәсілін пайдаланған жөн. Мысалы, A(1:k, j) операторы массивтың j -шы бағанасының элементтерін 1-ден k -ға дейін тізбектеп береді. Ал

sum(A(1:4, 4) )

командасы алдында қарастырылған төртінші бағананың элементерінің қосындысын есептеп береді. Бұл жерде қолданылған (:) -қос нүкте операциясының MATLAB жүйесіндегі маңызы зор. Мысалы, sum(A(:, end) ) командасы арқылы матрицаның соңғы бағанасының элементтерінің қосындысы алынады.

Басқа алгоритмдік тілдер сияқты нақты программа құру үшін MATLAB жүйесінде де математикалық сөйлемдер құрылады. Олардың құрамында

• айнымалылар;
• сандар;
• операторлар;
• функциялар

болады.

MATLAB жүйесінің тағы бір негізгі ерекшелігі ол айнымалылардың типін анықтауды қажет етпейді. Жаңадан кездескен айнымалыға MATLAB автоматты түрде өзінің жадынан орын бөледі, ал егер ол айнымалы бұрыннан бар болса, онда оның құрамын өзгертіп, қажет болса жадынан қосымша орын тағайындайды.

Айнымалылар әріптермен, цифрлармен және астын сызу символымен белгіленеді. MATLAB бас әріптермен кіші әріптерді бөліп қарайды. Мысалы, A мен a екі түрлі айнымалы.

MATLAB жүйесінде сандар ондық есептеу жүйесінде қарастырылады. Ондық дәреже e әріпімен көрсетіледі. Комплекс сандардың жорамал бөлігін белгілеуге i немесе j әріптері суффикс ретінде пайдаланылады. Төменде MATLAB жүйесінде сандардың дұрыс жазылуына мысалдар келтірілген:

3 -99 0. 0001

9. 6397238 1. 60210 e -20 6. 02252 e 23

1 i -3. 14159 j 3e5i .

Сандардың бәрі компьютердің жадында IEEE стандартымен анықталатын long форматымен сақталады. Жылжымалы нүктемен сипатталатын сандарда 16 мағыналы цифр болады да, олардың мәндері 10 ^-308 -ден 10 ³⁰⁸ -ге дейінгі диапазонда өзгереді.

MATLAB жүйесінде мынадай операторлар қолданылады:

+ қосу;

- алу;

* көбейту;

/ бөлу;

\ сол жақтан бөлу;

^ дәреже;

' дефис-транспондау белгісі;

() есептеу тәртібін көрсететін жақшалар.

MATLAB жүйесінде элементарлық математикалық функциялардың үлкен қоры бар. Мысалы, abs, sqrt, exp, sin және т. б. Жүйеде теріс сандардың квадрат түбірлері мен логарифдері де есептеліп, нетижесі комплкс сандар түрінде алынады. Сонымен қатар күрделі, Гамма функциясы мен Бессель

функцияларының да стандартты командалары бар. Барлық математикалық функциялардың тізімін алу үшін

help elfun

командасын қолданса болғаны.

Бірнеше арнайы функциялар жиі қолданылатын константаларды береді:

pi 3. 14159265 . . .

i жорамал бірлік,

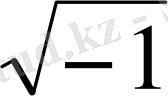
j мағынасы -мен бірдей

eps жылжымалы нүктелі санның салыстырмалы дәлдігі, 2 ^-52

realmin ең кіші жылжымалы нүктелі сан, 2 ^-1022

realmax ең үлкен жылжымалы нүктелі сан, 2 ¹⁰²³

Inf шексіздік

NaN сан емес дегенді көрсетеді. Бұл белгі 0/0 немесе Inf-Inf операцияларының математикалық мағынасы жоқ екені туралы ескертеді.

Бұл функциялардың мағыналарын қажетінше өзгертіп отыруға болады. Мысалы

eps=1. e-6 .

Функцияның бастапқы мәніне қайта оралу үшін

clear eps

командасы орындалады.

Матрицалармен жұмыс істеу

Матрицаларды жүйенің көмегімен де құруға болады. Ол үшін

• zeroбәрі ноль
• onesбәрі бір саны
• randкездейсоқ сандардың біркелкі таралуы
• randnкездейсоқ сандардың нормалды таралуы

командалары қолданылады. Соңғы екі команда математикалық статистика есептерінде қолданылатын болғандықтан оларға арнайы тоқталу қажет. Ал алдыңғы екі команда сандық қатар элементтерін өзара қосу, немесе көбейту операцияларында нәтиже жинақталатын матрицаларды тазалап алу үшін қолданылады.

MATLAB жүйесінде сандардың массивынан тұратын матрица мәтіндік файл түрінде құрылады. Төртбұрышты кестенің элементтері өзара бос орын арқылы бөлінеді және матрицаның қатарларындағы элементтер саны бірдей болу керек. Мысалы MATLAB жүйесінің сыртында 4 қатардан тұратын мәтіндік файл құрайық:

16. 0 3. 0 2. 0 13. 0

5. 0 10. 0 11. 0 8. 0

9. 0 6. 0 7. 0 12. 0

4. 0 15. 0 14. 0 1. 0

Файлды magik. dat деген атпен сақтайық. Енді

load magik. dat

деген команда осы файлды оқып, берілген матрицадан тұратын magik деген айнымалыны құрады.

Енді М-файлдарды құруды бастайық. Төменгі дәрежедегі алгоритмдік тілдерде программа деп аталатын қосымшаны MATLAB жүйесінде М-файл деп атайды. Бұл жүйеде алғаш рет жұмысты бастағанда жүйеге кірген бетте мониторда MATLAB-тың командалық терезесі ашылады. Командалық терезенің командалық қатарында командалар теріліп, программаның жұмысын басқаруды ұйымдастырады. Сонымен қатар, қомандалық терезе арқылы программаның жұмысын бақылап отыруға болады. Бұл терезеде программаның қателерінің түрі, олардың программада орналасқан жері және т. б. көрсетіліп отырады және соңында программа жұмысының нәтижесі көрсетіледі. Ал программаның өзін жазу үшін командалар терезесінде File тізімін ашу керек. Тізімнен New командасы арқылы жаңа терезе ашылады. Бұл терезеде жазылатын программаның аталуы және сақталатын орыны сұралады. Бұл сұрақтарға жауап берілген соң мәтіндік редактор деп аталатын жаңа терезе ашылады. Осы терезеге бұдан кейін М-файл деп аталатын жаңа программаның мәтіні орналастырылады (жазылады) . М-файл компьютердің жадында программаның берілген атына . m кеңейту қосылып сақталады. Бұдан кейінгі жұмыс тек командалық терезе мен мәтіндік редактор арқылы орындалады. Мәтіндік редакторда программаны жазып болғаннан кейін редактордың бас жағында Debug тізімінде орналасқан Run командасы басылады. Бұл кезде командалық терезе ашылып, онда программаның қателері, немесе есептің нәтижесі шығады. Есептің нәтижесіне де . m кеңейту қосылып жаңа ат беріледі. Жаңадан құрылған М-файлды (программаны) келесі жолы ашу үшін мәтіндік редактордағы File тізімінің Open командасын басылып, пайда болған тізімнен ізделіп отырған М-файл ашылады. Енді М-файлға өзгертулер енгізе беруге болады. Командалық терезе мен мәтіндік редактор жұмыс столында бірінің астына бірі орналасады. Қажет терезені шерту арқылы оларды кезекпен ашып отырады. Программаға енгізілетін әрбір өзгерістен кейін File тізіміндегі Save

немесе Save All командалары арқылы өзгертулерді жаттатып отыру керек. Мәтіндік редактордағы программаны дұрыстау барысында командалық терезеде көрінетін ақпараттардың көлемі өсіп кетіп, жұмыс істеуге кедергі жасайтын кезі жиі болады. Мұндай кезде командалық қатардағы >> символынан кейін clc командасын теріп Enter пернесін басу арқылы командалық терезені тазалауға болады. Бұл кезде компьютердің жадындағы ақпараттар жоғалып кетпейді. Олардың ішіндегі қажетті бөлігін бұрынғыша қайтадан командалық терезеге шығаруға болады.

Ақпарат ағымдарын басқару

MATLAB жүйесінде ақпараттар ағымын басқарудың бес түрі бар:

• ifоператоры
• switchоператоры
• forциклы
• whileциклы
• breakоператоры.

if операторы логикалық пікірді есептеп, нәтижесі ақиқат болса берілген операторлар тобын орындайды. Операторлар тобының құрамында қажет жағдайда қосымша шарттарды ескеретін elseif және else операторлары болуы мүмкін. if операторы end арнайы сөзімен аяқталады.

switch операторы case арнайы сөзімен бірге жұмыс істейді. switch операторында жақша ішінде арнайы тізім, логикалық шарт немесе есептеу алгоритмы орналасады. Жақшаның мәніне байланысты case орындалатын операторды (операторлар тобын) таңдайды. Нәтижесінде берілген шартқа сәйкес келетін алғашқы оператор (операторлар тобы) ғана орындалады. switch операторы end арнайы сөзімен аяқталады.

for циклы операторлар тобын берілген сан рет орындап шығуға арналған. Цикл end арнайы сөзімен аяқталады. Циклға мысал келтірейік:

for i=1:m

for j=1:n

H(i, j) =1/(i+j) ;

end

end

H

Циклдың ішінде орындалатын Н операторының соңында ; белгісі қойылмаса командалар терезесінде оператордың есептеу нәтижесі әрбір цикл үшін шығып отырады. Программаның соңындағы Н идентификаторы цикл жұмысын аяқтағаннан соң алынған нәтижені командалар терезесінен көрсету үшін жазылады. Егер бұл нәтиже қажет болмаса Н идентификаторынан кейін ; белгісін қояды, немесе Н белгісін жазбай кетеді. Программаның оқылуын жеңілдету үшін оның мәтінін жоғарыдағыдай сатылап орналастырған дұрыс.

while циклының орындалу саны логикалық шартпен анықталады. Төменде мысал ретінде while, if, else және end операторларының көмегімен жазылған полиномның түбірін қақ бөлу әдісімен анықтаудың программасы келтірілген.

a=0; fa=-Inf;

b=3; fb=Inf;

while b-a>eps*b

x=(a+b) /2;

fx=x^3-2*x-5;

if sign(fx) ==sign(fa)

a=x; fa=fx;

else

b=x; fb=fx;

end

end

x

Программаның жұмысы нәтижесінде x ³ -2x-5 полиномының

x=

2. 09455148154233

түбірі алынады.

break операторы for немесе while циклдарынан циклдың соңына жетпей шығып кетуге мүмкіндік береді. Егер программада бір бірінің ішінде орналасқан бірнеше цикл бар болса, онда break операторы тек өзі ішінде орналасқан циклдан ғана шығарады да, оның сыртындағы циклдың жұмысы жалғаса береді.

MATLAB жүйесінің жоғарыда келтірілген негізгі бөлігінің (ядро) мүмкіндіктері қаншалықты мол болғанымен әрқашан жаңадан пайда болып жататын жекелеген математикалық проблемаларды шешуге оның мүмкіндіктері жеткіліксіз болып жатады.

Мұндай жағдайларда уақтылы шешім қабылдап отыру үшін MATLAB жүйесінің негізгі пакетінің архитектурасы оған дер кезінде жаңа программалық шешімдер қосып отыруға бейім етіп жасалынған және мұндай өзгерістер қолданушы байқамайтындай етіп ұйымдастырылған. Себебі, қосымша пакет инсталяцияланғаннан кейін ол MATLAB жүйесінің негізгі пакетімен араласып кетеді де, оны пайдалану әдістерінің негізгі пакетті пайдалу әдістерінен айырмашылығы болмайды.

... жалғасы

Эллипс тектес теңдеулерді шекті айырымдар және шекті элементтер әдістерімен шешудің мүмкіндіктерін зерттеу

Жылуөткізгіштік теңдеуін нүктелік жылу көзін ескеріп шекті элементтер әдісімен шешу

ЖЫЛУӨТКІЗГІШТІКТІҢ ТЕҢДЕУЛЕРІНІҢ КЕЙБІР БАСТАПҚЫ-ШЕКТІК ЕСЕПТЕРІН САНДЫҚ ӘДІСТЕРМЕН ШЕШУ

Атомдарды жақындатқанда электрон күйлерінің өзгеруі

Қатты денелердің жылу өткізгіштігі мен катты денелердің молекула-кинетикалық теориясының негізгі ұғымдары ондағы тасымалдау процестері, соның ішінде стационар және стационар емес жағдайлардағы жылу өткізгіштік процесі

Жылу қондырғылары және олардың еліміздің мұнай саласындағы ролі

Ампулалық құрылғылар

Тоңдық жер бедерінің қалыптасуы мен дамуы

Физика пәнінен дәріс сабақтарының мән жазбалары

Жерасты ағындары

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс