Центрлік проекциялау. Параллель проекциялау

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Центрлік проекциялау. Параллель проекциялау

Табылған А ¹ В ¹ С ¹ үшбұрышы АВС үшбұрышының кескіні болады. п ¹ жазықтығын проекциялар жазықтығы, S нүктесін проекциялау центрі, ал АS, ВS және СS түзулерін проекциялаушы түзулер деп атайтынын білеміз. А ¹ В ¹ С ¹ үшбұрышын АВС үшбұрышының п ¹ жазықтығындағы центрлік проекция деп атайды. Нәрсенің кескінін осылай табуды центрлік проекциялау дейді. Осындай өздеріне өздері проекцияланатын нүктелерді қозғалмайтын нүктелер (инвариантгар) деп атайды. Центрлік проекциялаудың негізгі қасиетгері:

нүкте нүктеге кескінделеді;
проекциялаушы түзулерден өзге түзулер нүктеге кескінделеді, ал проекциялаушы түзу нүктеге кескінделеді;
егер түзу нүкте арқылы өтсе, онда тузудің проекциясы арқылы өтеді.

Проекциялау центрі өзіндік емес нүкте болатын центрлік проекцияның жеке түрін параллель проекция деп атайды. Өзіндік емес нүкте өзіндік тузудің көмегімен анықталатындытан проекциялау аппараты бұл жағдайда проекциялар жазықтығынан және шексіз қашықтықта жатқан 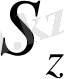нүктесі арқылы ететін, проекциялау бағыты деп атапатын 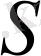түзунен тұрады. Табылған А ¹ нүктесін А нүкгесінің п' жазықтығындағы 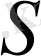бағытындағы параллель проекциясы, а ¹ түзуін а түзуінің және түзуін 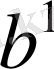түзуінің параллель проекциясы деп атайды. Нәрсенің кескінін осылайша табуды параллель проекциялау дейді. Параллель проекциялауда да нүкте нүктеге, проекциялау бағытына параллель емес түзу түзуге проекцияланады және өзара меншіктілік сақталады. Проекциялау бағытына параллель түзулер проекциялаушы түзулер деп аталады. Жалпы алғанда проекциялаушы жазыктық деп проекциялау бағытына параллель жазықтықты айтады. Проекциялаушы жазыктық тузуге проекцияланады. Тузуді берілген қатынаста бөлудің орнына онын кескінін берілген қатынаста бөлуге болады. Проекциялар жазықтығына параллель жазык фигураның параллель проекциясы сол фигураның өзіне тең болады.

Түзудің жазықтыққа перпендикулярлық белгісі - түзу жазықтықтын қиылысатын екі түзуіне перпендикуляр болуы қажет. Бұл айтылғанның дұрыстығы стереометрияда дэлелденеді.

А нүктесінен П жазықтығына түсірілген перпендикулярдың табаны 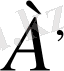нүктесін П' жазықтығындағы тік бұрышты проекциясы деп атайды.

Нәрсенің тік бұрышты проекциясын салуды оны тік бұрыштап проекцияпау дейді. Проекция жазыктығына перпендикуляр түзулер проекциялаушы түзулер болады. Проекциялаушы түзулер нүктеге проекцияланады.

Проекция жазықтығына перпендикуляр жазыктықты проециялаушы жазықтық деп атайды. Проекциялаушы жазықтықга жатқан нүктенің, кесіндінің және жазық фигураның проекциясы сол жазықтықтың проекциясы бойында жатады.

Проекциялар жазықтатынын әрбір нүктесіне кеңістікте оны проекциялаушы түзудің барлық нүктелері сәйкес болады, яғни сәйкестік бірмәнді болмайды. Басқаша айтқанда, бір проекциядан тұратын кескін нүктенің кеңістіктегі орнын анықтай алмайды. Нәрсенің формасын және кеністіктегі орнын анықтауға мүмкіндік бермейтін кескіндерді қайтымсыз деп атайды.

Кеңістікгегі нүктенің орнын анықтау үшін оның үш координатасы белгілі болуы керек. Фигура мен оның кескіні арасында өзара бірмәнді сәйкестік орнату үшін фигураның әрбір нүктесіне кескіннің белгілі бір нүктесі сәйкес болуы керек және керісінше, кескіннің әрбір нүктесіне фигураның белгілі бір нүктесі сәйкес болуы қажет.

Нәрсенің формасын және кеңістікгегі орнын анықтауға мүмкіндік беретін кескіндерді қайтымды кескіндер деп атайды.

Сонда 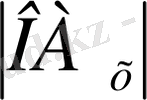берілген нүкгенің абсциссасын, 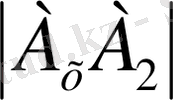- ординатасын және А ₂ А - аппликатасын анықтайды. 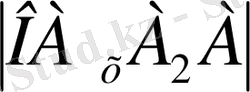сынық сызығын А нүктесінін натурал координаттың сынық сызығы дейді, ал Охуz жүйесін натурал координаттар жүйесі дейді.

Проекциялау бағыты проекция жазықтығына перпендикуляр болса аксонометрия тік бұрышты деп аталады. Тік бұрышты аксонометрия үшін . Егер проекциялау бағыты проекция жазықтығына перпендикуляр болмаса, аксонометрия қиғаш бұрышты деп аталады. Жалпы жағдайда 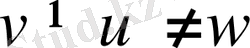болуы мүмкін. Аксонометрияның 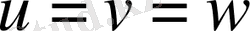болатан жеке түрін изометрия дейді («изометрия» грек сөзі, қазақшаға аударғанда «бірдей өлшем» деген мағына береді), ал бүрмалану көрсеткіштерінің екеуі өзара тең және олар үшіншісіне тең болмайтын түрін диметрия деп атайды («диметрия» грек сөзі, «екі өлшем» дегенді білдіреді) .

Аксонометриялық проекциялар жазықтығының натурал жүйеге қарағандағы орналасуына және проекциялау бағатына байланысты аксонометрялық осьтердің арасындағы бұрыш әр түрлі болуы мүмкін, оларға ешқандай шек қойылмайды. Тік бұрышты аксонометрия үшін 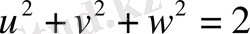болады. Сондықган бұрмалану көрсеткіштерінің екеуін қалауымызша тағайындауға болады. Осы айтылгандардан аксонометрияның өте көп екенін аңғарамыз. Біз олардың екеуімен ғана танысамыз. Олар - тік бұрышты изометрия мен қиғаш бүрышты фронталь диметрия.

Түзуді екі нүкте, ал жазықтықты бір түзудің бойында жатпайтын үш нүкте анықтайтыны белгілі. Екі нүкте арқылы өтетін тек жалғыз түзу, ал үш нүкте арқылы өтетін тек жалғыз жазықтық салуға болады. Сондыктан түзудің аксонометриясын салу, ал жазыктықтың аксонометриясын салу үшін оның үш нүктесінің аксонометриясын салу жеткілікті.

Проекциялау бағытына параллель болмайтын жазықтықтың проекциялау әдісімен алынған кескінін қарастыратын болсақ, онда ол кескін қағаз бетін түгел алып жатар еді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.