Материялық нүктенің шеңбер бойымен бірқалыпты қозғалысы: бұрыштық және сызықтық сипаттамалар, центрге тартқыш үдеу


ШЕҢБЕР БОЙЫМЕН БІРҚАЛЫПТЫ ҚОЗҒАЛЫС
Бұған дейін біз түзусызықты қозғалыстарды зерттедік, олардың траекто-риялары - түзусызықтар. Алайда көп жағдайларда қозғалыс қисықсызық бойымен өтеді. Мысалы, жазып отырған қаламсабыңның ұшы да қисықсызықпен қозғалады, көкжиекке бұрыш жасай лақтырылған дене де қисықсызықты траекториямен қозғалады. Автомобиль бір жолдан екінші жолға өткенде де қисықсызықты қозғалады, барлық ғарыштық денелер де қисықсызықты қозғалады.
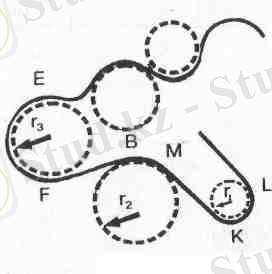
Қисықсызықты қозғалыстардың барлық түрін зерттеп білу мүмкін емес, оның қажеті де жоқ, өйткені кез келген қисықсызықты қозғалысты шеңбер доғалары бойымен өткен қозғалыстардың тізбегі деп қарастыруға болады (1-сурет) .
Сондықтан біз алдымен материялық нүктенің шенбер бойымен қозғалысын зерттейміз де шыққан заңдылықтарды, егер бұл мүмкін болса, қисықсызықты қозғалыстардың басқа түрлеріне пайдаланамыз.
МАТЕРИЯЛЫҚ НҮКТЕНІҢ ШЕҢБЕР БОЙЫМЕН БІРҚАЛЫПТЫ ҚОЗҒАЛЫСЫ
Дененің шеңбер бойымен қозгалысына мыналар мысал бола алады:
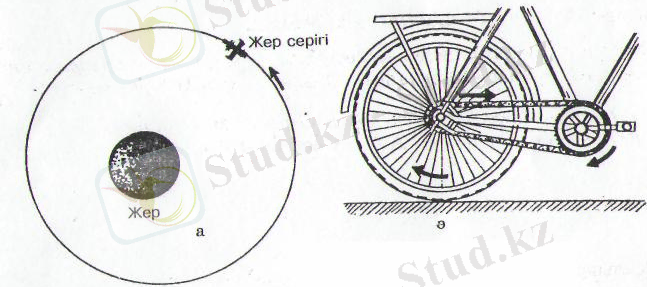
а) дөңгелек орбитамен Жерді айнала қозғалған жасанды серіктің қозғалысы (2-сурет) ;
ә) айналып тұрған дененің қайсыбір нүктесінің қозғалысы (2-сурет)
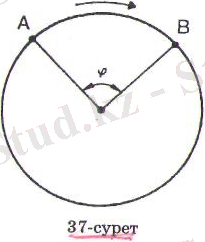
1. Бұрыштық ығысу. Материялық нүкте шеңбер бойымен бірқалыпты қозғалсын және бұл нүкте t 1 мезетіндегі А қалпынан t 2 мезе-тіндегі В қалпына орын ауыстырсын (3-сурет) . Шеңбердің центрінен материялық нүктеге жүргізілген радиус осы уақыт ішінде бұрышын сызады, оны бұрыштың ығысу деп атайды.
Халықаралық бірліктер жүйесінде бұрыштық ығысу радианмен өлшенеді.
Радиан дегеніміз шеңбердің екі радиусының арасындағы центрлік бұрыш. Бұл екі радиустың арасындағы доғаның ұзындығы шеңбердің радиусына тең. Оны қысқаша 1 рад деп белгілейді.
2. Айналу жиілігі және айналу периоды. Нүктенің шеңбер бойымен бірқалыпты қозғалысын сипаттау үшін арнаулы екі шама: айналу жиілігі мен айналу периодын енгізу қабылданған.
Айналу жиілігі деп материялық нүктенің айналу центрінің маңында бір секунд ішінде жасайтын айналым санын айтады. Айналу жиілігі гректің v (ню) әрпімен белгіленеді:
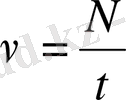
мұндағы N - t уакыт ішіндегі айналу саны.
Халықаралық Бірліктер жүйесінде жиілік бірлігіне 1 секунд ішінде жасаған 1 айналым қабылданған. Оны қысқаша 1с -1 деп белгілейді.
Айналу периоды деп нүктенің шеңбер бойымен бір айналым жасауға кеткен уақытын айтады. Айналу периоды Т әрпімен белгіленеді:
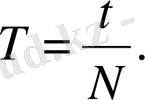
Халықаралық бірліктер жүйесінде периодтың бірлігі үшін 1секунд қабылданған.
Период пен жиілік бір-біріне кері шама екенін байқау қиын емес:
және
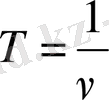
3. Бұрыштық жылдамдық . Дененің шеңбер бойымен қозғалысын бұрыштық жылдамдықпен сипаттайды. Ол бұрыштық орын ауыстырудың осы орын ауыстыруға кеткен уақытқа қатынасына тең.
Бұрыштық жылдамдық
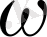 (омега) әрпімен белгіленеді:
(омега) әрпімен белгіленеді:
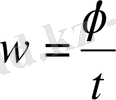
Материялық нүкте шеңбер бойымен тұрақты бұрыштық жылдамдықпен қозғалатындай қозғалысты шеңбер бойымен бірқалыпты қозгалыс деп атайды.
Халықаралық бірліктер жүйесінде бұрыштық жылдамдық бірлігіне орын ауыстыруы секундына 1 радианға тең болатын дененің шеңбер бойымен бірқалыпты қозғалысының жылдамдығы алынады. Бұрыштық жылдамдықтың бұл бірлігі секунд есебі мен алыған радиан (1секундтағы радиан) деп аталады да, 1 рад/с деп белгіленеді.
Т периодта бұрыштық орын ауыстыру 2
- ге тең болады.
Сондықтан бұрыштық жылдамдық
немесе
екенін
ескерсек, онда
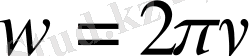 екені шығады.
екені шығады.
Шеңбер бойымен бірқалыпты қозғалатын
дененің сызықтық жылдамдығы
1. Сызықтық жылдамдық. Материялық нүкте радиусы
R
- ге тең шеңбер бойымен бірқалыпты қозғалсын делік. Нүтенің қозғалысы бірқалыпты болғандықтан, жылдамдық модулі тұрақты болады. Айталық, өте аз
 уақыт ішінде нүкте
А-
дан
В
-ға орын ауыстырды делік (көрнекілік үшін 4-суретте
А
1
В
1
ығысуы үлкейтіліп көрсетілген) .
уақыт ішінде нүкте
А-
дан
В
-ға орын ауыстырды делік (көрнекілік үшін 4-суретте
А
1
В
1
ығысуы үлкейтіліп көрсетілген) .
Сонда жылдамдықтың жалпы анықтамасы бойынша
А
1
В
1
бөлігіндегі сызықтық жылдамдық
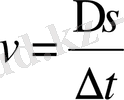 болады және
А
1
В
1
хордасының бойымен бағытталады. Ал
болады және
А
1
В
1
хордасының бойымен бағытталады. Ал
 уақыты кеміген сайын хорда доғаға жақындай береді де,
А
1
В
1
бөлігінің ортасында (С нүктесінде) жылдамдық векторы доғаға жүргізілген жанама бойымен бағытталады. Олай болса, лездік жылдамдық жанама бойымен бағытталған.
уақыты кеміген сайын хорда доғаға жақындай береді де,
А
1
В
1
бөлігінің ортасында (С нүктесінде) жылдамдық векторы доғаға жүргізілген жанама бойымен бағытталады. Олай болса, лездік жылдамдық жанама бойымен бағытталған.
Бұған айналып тұрған қайрақ тасқа болат шыбықтың ұшын тигізіп көз жеткізуге болады. Тастан үшып шықкан қызған бөлшектер өздерінің алған жылдамдықтарымен ұшқын түрінде көрінеді.
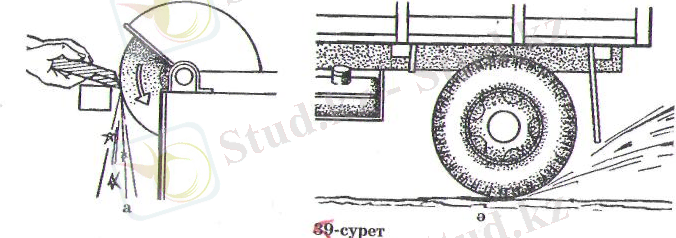
Ұшқынның бағыты болат шыбықтың қайрақ тасқа тиген жеріндегі шеңбердің нүктесіне жүргізілген жанаманың бойымен бағытталады
Шеңберге жүргізілген жанама бойымен қозғалысқка тұралап қалған автомобиль доңғалағынан шашыраған балшық та мысал бола алады (5, ә-сурет) .
Сонымен, шеңбер бойымен қозғалған дененің сызықтың жылдамдығы модулі жағынан тұрақты, ал бағыты бойынша үздіксіз өзгеріп отырады және траекторияның кез келген нүктесіне жүргізілген жанаманың бойымен бағытталады.
Сызықтық жылдамдықтың модулі тұрақты болғандықтан, оның шамасын мына формуламен анықтауға болады:
. Бір айналым ішінде (t = Т) дене шеңбер ұзындығына тең арақашықтықты жүріп өтеді: s = 2
R . Сондықтан
немесе
екенін ескерсек

2 . Бүрыштық және сызықтық жылдамдықтар арасындағы қатыс. Сызықтық жылдамдықтың бұрыштық жылдамдықка қатынасын табайық:
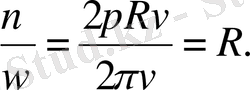 Сонымен
Сонымен
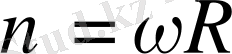 және
және
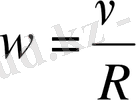
ШЕҢБЕР БОЙЫМЕН БІРҚАЛЫПТЫ
ҚОЗҒАЛҒАН ДЕНЕНІҢ ҮДЕУІ
Шеңбер бойымен бірқалыпты қозғалған дененің сызықтық жылдамдығы модулі бойышна тұрақты болғанымен бағыты бойынша үздіксіз өзгеріп отырады. Бірақ бағыты бойынша жылдамдықтың өзгеруі - дененің шеңбер бойымен бірқалыпты қозғалысы кезінде үдеудің бар екенін білдіреді. Осы үдеу центрге тартқыш үдеу деп аталады.
1.
Центрге тартқыш үдеу
. Анықтама бойынша үдеу жылдамдықтың өзгеру тездігін сипаттайды және жылдамдық өзгерісінің осы өзгеріске кеткен уақытқа қатынасымен өлшенеді, ал оның бағыты жылдамдық өзгеруі векторының бағытымен дәл келеда:
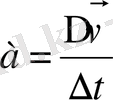 немесе скаляр түрде
немесе скаляр түрде
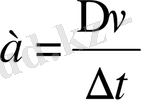 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz