ДИФФЕРЕНЦИАЛДЫҚ ЕСЕПТЕУДІҢ НЕГІЗГІ ТЕОРЕМАЛАРЫ ФЕРМА, РОЛЬ, ЛАГРАНЖ, КОШИ ТЕОРЕМАЛАРЫ

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

Қостанай мемлекеттік педагогикалық институт

Жаратылыстану-математикалық факультеті

Физика-математика кафедрасы

Жумабаева Назира Бердыбаевна

ДИФФЕРЕНЦИАЛДЫҚ ЕСЕПТЕУДІҢ НЕГІЗГІ ТЕОРЕМАЛАРЫ: ФЕРМА, РОЛЬ, ЛАГРАНЖ, КОШИ
ТЕОРЕМАЛАРЫ

Курсовая работа

Ғылыми жетекші
... ... .

Қостанай, 2018 г.
Мазмұны

Кіріспе 3
1 Дифференциалдық есептеулердің тарихы мен ерекшеліктері 5
1.1 Дифференциалдық есептеулердің пайда болуы 5
1.2 Дифференциалдық есептеулердің тарихы мен ерекшеліктері 7
2 Дифференциалдық есептеулердің негізгі теоремалары және оларды
әр түрлі есептерде қолдану 11
2.1 Ферма және Ролль теоремалары 11
2.2 Лагранж және Коши теоремалары 14
2.3 Дифференциалдық есептеу арқылы практикалық есептерді шешу мысалдары
19
Қорытынды 22
Пайдаланған әдебиеттер тізімі 24

Кіріспе

Ғылымның, техниканың және экономиканың өніп-өркендеуіне математикальқ
зерттеу, модельдеу және жобалау әдіс-тәсілдерінің колданылуы ерекше әсер
ететіні белгілі. Бұған қaзipri кезеңдегі eceптeriш техникалардьң айрықша
түрлерінің дамығандығы және компьютерлік жүйенің өмірдегі және табиғаттағы
ic әрекеттердің баршасына жаппай араласуының мәні зор болып отыр. Осылардан
- математикалық әдіс-тәсілдері өмірлік нақтылы есептерге колдана білудің
ауқымы ұлғайды.
Мектеп математикасы курсындағы функция ұғымы негізгі ұғымдардың біріне
жатады. Функциялық тәуелділік өмірдегі өзгерісті нақты және толық түрде
кескіндеуге мүмкіндік береді, ол шамалар арасындағы өзара байланысты
түсініп анықтауға үлкен септігін тигізеді.
Жұмыстың бірінші тарауында регуляр шекаралық шарттардың әр түріне жеке
тоқталып, төртінші ретті дифференциалдық оператор үшін регуляр, оның ішінде
күшейтілген және күшейтілген емес шекаралық шарттарды бөліп алып. Сол әр
шарттқа сәйкес дифференциалдық оператордың меншікті функцияларының
асимптотикасын алып, олардың базис болу болмауын тексереміз.
Шекаралық шарттар күшейтілген регуляр болған жағдайда оператордың
меншікті және қосалқы функциялары 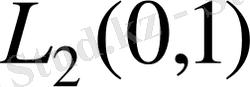кеңістігінде Рисс базисін құратыны
белгілі. Бұл айтылғанды ең алғаш В.П. Михайлов көрсетті. Дәл осы нәтиже
Кессельман Г.М. жұмыстарында, және Данфорд Н. мен Шварц Т. монографиясында
бар. Бұл жұмыстардың барлығында да, дәлелдеу оператор мен оның түйіндес
операторының нормаланған меншікті және қосалқы функциялар жүйесінің
бесселдік екендігіне әкелінді.
Кессельман Г.М. жұмыстарында шекаралық шарттары регуляр бірақ
күшейтілген емес регуляр болатын дифференциалдық оператордың меншікті және
қосалқы функциялары базис құрмайтындай мысалдар көрсеткен. Себебі бұл
жағдайларда оператор Данфорд Н. мағынасында спектральды болмайды, демек бұл
жағдайда оператордың меншікті және қосалқы функциялары Рисс базисін
құрмайтыны белгілі. Бұл жайтты, оператордың меншікті мәндері асимптотикалық
жақын орналасқандығымен түсіндіруге болады, демек келесідей асимптотикаға
ие

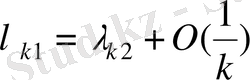
болғанда. Соның ішінде жақын орналасқан меншікті мәндерге сәйкес
меншікті функциялар бір біріне тең емес, бірақта арасындағы бұрыш нөлге
ұмтылады. Дәл осындай жағдайларда оператордың меншікті және қосалқы
функциялар жүйесі базис құрмайды.
Екінші ретті дифференциалдық операторларға қарағанда төртінші ретті
шекаралық шарттары күшейтілген емес регуляр болатын дифференциалдық
операторлардың спектральдық теориясы азырақ дамыған. Бұған байланысты тек
жекеленген жұмыстар ғана бар.[3,4] Бұл дипломдық жұмыста алдағы уақытта дәл
осы шекаралық шарттар күшейтілген емес регуляр болатын төртінші ретті
дифференциалдық операторлардың спектральдық қасиеттері зерттеледі.
Ал екінші тарауда екінші ретті дифференциалдық оператордың ойылған
кесіндідегі Гельфанд – Левитан формуласы тектес бірінші регуляризацияланған
ізі есептелген.

1 Дифференциалдық есептеулердің тарихы мен ерекшеліктері

1.1 Дифференциалдық есептеулердің пайда болуы

Математикалық анализ — математиканың функцияларды дифференциалдық және
интегралдық есептеулер әдістерімен зерттейтін бөлімі. Математикалық
анализдің негізгі зерттеу құралы — шектер әдісі. Математикалық анализдің
дамуы нәтижесінде функциядан кеңірек ұғым функционал, оператор ұғымдары
пайда болды. Табиғат пен техникада функциялар арқылы құбылыстар,
қозғалыстар көптеп кездеседі. Сондықтан Математикалық анализдің
функцияларды зерттейтін құрал ретіндегі маңызы зор. Ол математиканың үлкен
бөлігін қамтиды. Оған жалпы жағдайда дифференциалдық есептеу және
интегралдық есептеу, нақты және жорымал айнымалы функциялар теориясы,
комплексті айнымалы функциялар теориясы, жуықтау функциясы, дифференциалдық
теңдеулер теориясы, интегралдық теңдеулер теориясы, дифференциалдық
геометрия, вариациялық есептеулер, функционалдық анализ, т.б. математиканың
бөлімдері кіреді[1].
Тарихы. 17 ғасырға дейін Математикалық анализдің дербес есептер
шешімінің жиынтығы ретінде ғана танылды. Әрбір есептер мен дербес топтар өз
әдістерімен шешілді. 17 — 18 ғасырларда И.Ньютон, неміс математигі әрі
физигі Г.Лейбниц (1646 — 1716), Ресей физик-математигі, механигі Л.Эйлер
(1707 — 1783), француз математигі және механигі Ж.Лагранж (1736 — 1813),
т.б. ғалымдардың еңбектерінде бір жүйеге келтірілді. Ал Математикалық
анализдің базасы — шектер теориясын 19 ғасырдың басында француз математигі
О.Коши (1789— 1857) жасады[2].
Дифференциалдық есептеу — математикалық анализ бөлімі, онда туынды және
дифференциал ұғымы және функцияларды зерттеуіне оларды қолдану әдістері
зерттеледі[3].
Қолданбалы, ал кейін ғылыми әдіс ретінде дифференциалдық есептеудің
қалыптасуына Николай Кузанскиймен жасалған түзеу философиялық теорияның
пайда болуы алғы шарт болды. П.П. Гайденко былай деп жазды: Кузанскийдің
жұмыстарын бұл тұрғыдан зерттеп, дифференциалдық есептеуді жасау есептеу
техникасының практикалық қажеттіліктерімен ғана ынталандырылған жоқ,
сонымен қатар философиялық-теориялық ойлармен, континуум мен сан,
үзіліссіз бен бөлінбейтін, кеңістік және қозғалыс проблемаларын жаңадан
шешу ұмтылысымен дайындалған деген қорытындыға келуге болады [4]. Расында,
Николай Кузанскийдің жұмыстарын антикалық ғылымнан бастап пікірлердің
эволюциялық дамуы деп есептеуге болады. Николай Кузанский математик
болмаған дерегін назарға алып, математикалық әдістің дамуына оның қосқан
үлесін асыра бағалауға болмайды. Ол алғаш рет арифметиканы ең дәл ғылым
ретінде қарастырудан кетті, сонысымен антикалық математикаға күмән
туғызды. Антикалық математиктер бірыңғай, бірлікті әмбебап критерий деп
есептеді. Кузанский өз кезегінде өлшем ретінде нақты санды емес,
шексіздікті келтіріп басқа көзқарасты ұсынады. Сонымен, ол математикадағы
дәлдікті ұғынуды терістетеді[5].
Николай Кузанский алғы тартқан тұжырымдамаларында шексіздік және
бірлік ұғымдарын ұштастырған Кавальери және Галилеоның еңбектерінің әсерін
байқау қиын емес. Алайда Николай Кузанскийдің Жорамалдар туралы еңбегі
дифференциалдық есептеуге сілтемесі бар жалғыз жұмыс болып табылмайды.
Мысал ретінде Болмыс-мүмкіндіктері туралы атауымен еңбекті келтіруге
болады, онда философ әлемді заттар жиынтығы ретінде емес, процесс ретінде
қарастырады. Мұнда ол маңызды термин – мүмкіндік-болмыс дегенді
шығарады[6]. В.Ф. Шаповаловтың Ғылым және техника философиясы: ғылым және
техника мағынасы туралы және ғылыми-техникалық дәуірдің жаһандық қауіп-
қатерлері туралы мақаласында бұл терминді әлемдік болмыстың
дифференциалы ретінде анықтайды және келесідегіндей ашады: Бұл сығылған
(немесе тартылған) максимум, және сондай ретінде ол өзімен жоғары, тамаша
максимумның ұқсастығын елестетеді [7].
Дифференциалдық есептеудің дамуы туралы айтқанда, мүмкін, осы әдістің
қалыптасу процесіне ең маңызды үлес енгізген екі есімнаманы айналып өтуге
болмайды: Исаак Ньютон және Готфрид Лейбниц. Осы ұлы ғалымдармен құрылған
математикалық құралдар қазіргі заманғы математиканың негізі болып табылады.
Ньютон-Лейбниц деп аталатын формула немесе іс жүзінде дифференциалды және
интегралды есептеудің байланыстырушы буыны болып табылатын анализдің
негізгі теоремасы жарқын үлгі болып табылады. Осығани байланысты әсіресе
қызықты факт Ньютон және Лейбниц параллельді және бір бірінен тәуелді емес
шамамен бір уақытта дифференциалдық есептеу аппаратын құрғаны болып
табылады[8]. Брокгауз және Ефрон Энциклопедиялық сөздігінен Д. А. Гравенің
"Дифференциалдық есептеу" мақаласында: "жаңа есептеудің идеясы соншалықты
піскен және, былайша айтқанда, санасында жүрді, Ньютон мен Лейбниц мүлде
тәуелсіз, келіспей және бір-бірінен алмай ашуды істей алғаны әбден әрине
табиғи[9]" деп жазады. Шын мәнінде, бұл мақалада бұрын айтылғандай, ұзақ
уақыт бойы көптеген ғалымдар еңбегімен жемістер үлкен, формаланған,
жүйеленген және нәтижесінде XVII ғасырдың аяғында екі ең көрнекті
математиктармен дамыған теорияға қалыптасқан. Осылайша, бұл мысал
математика тарихында ғылымдағы бірқатар алдыңғы ізденістер негізінде ірі
ашу жасалатынын айқын дәлелі болып табылады [10].
Келтірілген тұжырымдамаларды қорытындылай келе, дифференциалдық есептеу
және оның негізгі принциптері – бұл антикалық ғылым мен жаңа уақыт ғылым
арасындағы шекара деп тұжырымдауға болады. Өйткені дәл осы әдісті дамыту
шеңберінде жеке алынған ғылыми пәнді ғана емес, тұтас ғылым әдістемесін
түрлендірген математикаға көзқарастарды бағалау жасалынды. Маңызды ғылыми
әдіс ретінде дифференциалдық есептеудің даму тарихының ең маңызды
ерекшеліктерінің бірі, оның XVI-XVII ғғ. көптеген танымал ғалымдарда
қолданбалы әдіс ретінде бастапқы туындауы болды, олардың көпшілігі сол
немесе өзге түрде сонау XV ғасырда баяндалған Николай Кузанскийдің
идеяларын жалғастырды. Мұндай бастау үлкен білім мен пайымдауларды
қалыптастыруға мүмкіндік берді, бұл толыққанды, ал кейіннен дүниені танудың
маңызды, ғылыми математикалық әдісі ретінде дифференциалдық есептеуге
ресімделуіне әкелді.

1.2 Дифференциалдық есептеулердің тарихы мен ерекшеліктері

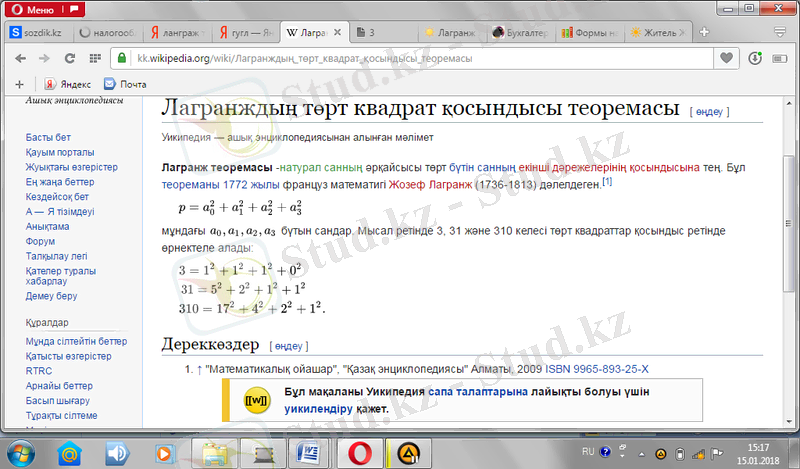
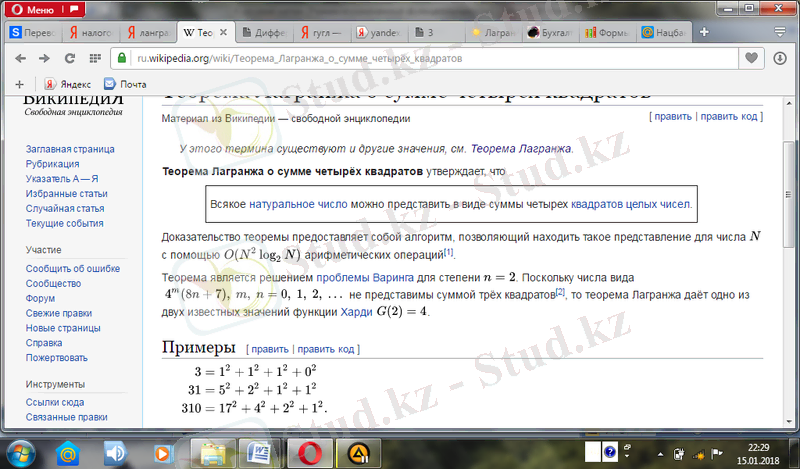
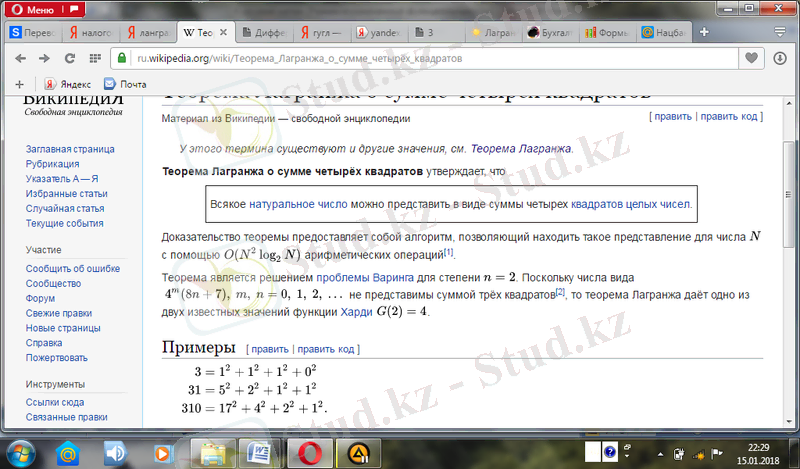
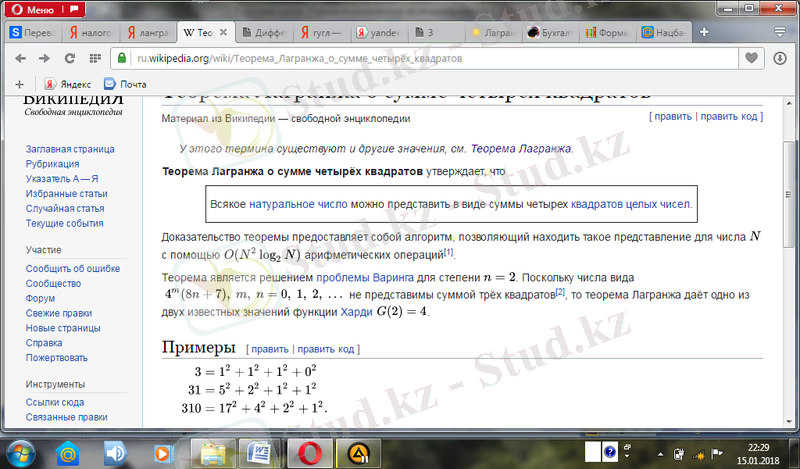
Лагранж теоремасы -натурал санның әрқайсысы төрт бүтін санның екінші
дәрежелерінің қосындысына тең. Бұл теореманы 1772 жылы француз
математигі Жозеф Лагранж (1736-1813) дәлелдеген[11].

{\displaystyle p=a_{0}^{2}+a_{1}^{2}+a_{2}^{2}+a_{ 3}^{2}\ }
мұндағы {\displaystyle a_{0},a_{1},a_{2},a_{3}} бүтін сандар.
Мысал ретінде 3, 31 және 310 келесі төрт квадраттар қосындыс ретінде
өрнектеле алады:

Төрт квадрат сомасы туралы Лагранж теоремасы теореманы дәлелдеу
саны үшін арифметикалық операциялар көмегімен мұндай түсінік
табуға мүмкіндік беретін алгоритм танытады деп тұжырымдайды [1].
Теорема дәрежесі үшін Варинг мәселесінің шешімі болып табылады.
Өйткені санының түрі үш квадраттың сомасымен ұсыныла алмайды [12],
онда Лагранж теоремасы Хардидың екі белгілі функциясы мәндерінің
бірін береді.
Теоремаларды бекіту алғаш рет 1621 жылы Башемен латынға аударылған
Диофант Арифметикасында пайда болды. Теорема үшін маңызды төрт квадраттың
сомаларының туындысы төрт квадрат сомасы болып табылады деген лемманы Эйлер
дәлелдеді, ол теореманың өзін дәлелдеуге жақын болды және жеке Лагранж үшін
көп іс жасады. Алайда, Лагранж Эйлерді озып кетті және 1770 жылы теореманы
дәлелдеді [13].
Ферманың Ұлы теоремасы (немесе Ферманың соңғы теоремасы) —
математикадағы ең әйгілі деуге болытын теоремасы; оның шарты орта мектеп
білімі деңгейінде тұжырымдалғанымен, дәлелдеу үшін көптеген мықты
математиктер ұзақ уақыт бастарын қатырды. Теорема былай дейді:
Кез келген бүтін

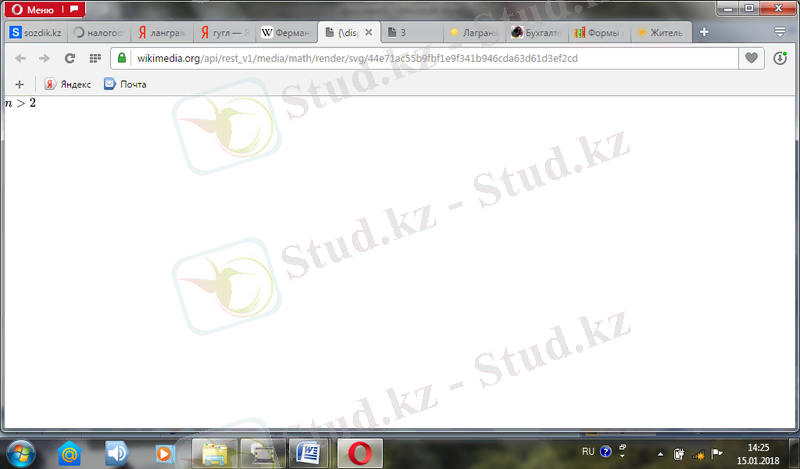
{\displaystyle n2}

үшін

{\displaystyle a^{n}+b^{n}=c^{n}\,\!}

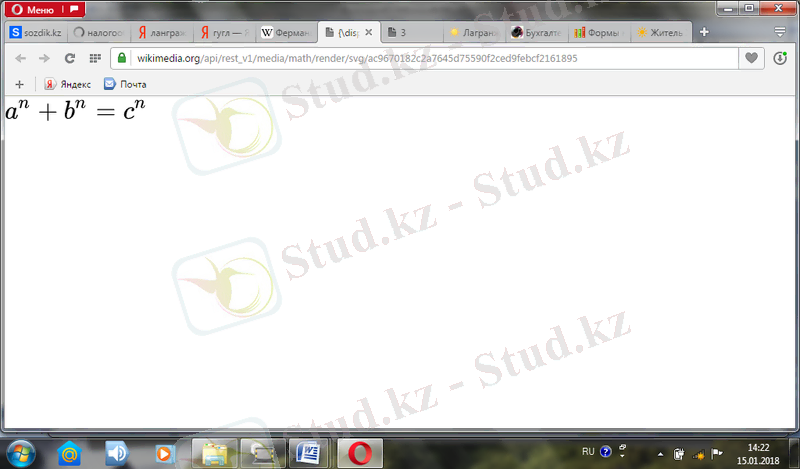
теңдеуінің натурал

{\displaystyle a}

,

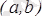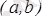
{\displaystyle b}

және

{\displaystyle c}

шешуі болмайды.
Пьер Ферманың 1637 тұжырымдаған осы теоремасы Диофанттың Арифметика
атты кітабы беттерінде "мен тапқан алғырлық дәлелдеме осы бетке сыйдыруға
өте ұзақ болады" деген сөздермен басылып шығады. Кейін Ферма {\displaystyle
n=4}n = 4 үшін шешуін жариялайды, алдыңғы алғырлық дәлелдеуі туралы осы
жолы ол тіс жармағандықтан жалпы түрде дәлелдегені күмәнді[14].

1670 жылғы Диофанттың Арифметикасында Ферманың соңғы теоремасы
(Observatio Domini Petri de Fermat) жайлы коментарийі бар.

Эйлер 1770 жылы теореманы {\displaystyle n=3} n = 3 үшін, ал Дирихле
мен Лежандр 1825 жылы {\displaystyl e n=5} үшін n = 5 дәлелдейді. Өз
үлестерін дәлелдеуге Ламе, Софи Жермен, Куммер және т. б. көптеген алдыңғы
қатарлы математиктер қосты. Теореманы дәлелдеуге деген талпыныс
қазіргі сандар теориясының көптеген нәтижелерін табуға алып келді[15].
Фальтингстың 1983 жылы дәлелдеген Морделла гипотезасынан {\displaystyle
a^{n}+b^{n}=c^{n}} теңдеуінің {\dis playstyle n3} болғанда тек
шектеулі өзара жай шешуі болатындығы шығады.
Дәлелдеудің соңғы қадамын тек 1994 жылдың қыркүйегінде Уайлс
Эндрю жасады. 130-беттік дәлелдеу Annals of Mathematics журналында
жарыққа шығады[16].
Ферманың кіші теоремасы — сандар теориясының классикалық теоремасы
былай дейді:
Егер p — жәй сан және a p-ға бөлінбесе, онда a p —
1 ≡ 1 (mod p)  (немесе a p — 1 — 1 p-ға бөлінеді).
Басқаша тұжырымдасақ,
Кез келген жәй p мен бүтін a үшін a p — a p-ға бөлінеді.
Дәлелдеуі.
Кез келген жәй p және бүтін теріс емес a үшін {\displaystyle a^{p}-
a} 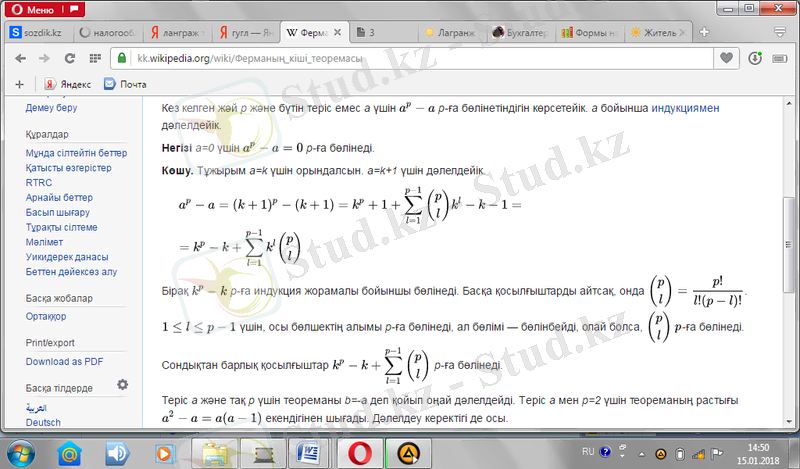p-ға бөлінетіндігін көрсетейік. a бойынша индукциямен д әлелдейік.
Негізі a=0 үшін {\displaystyle a^{p}-a=0} 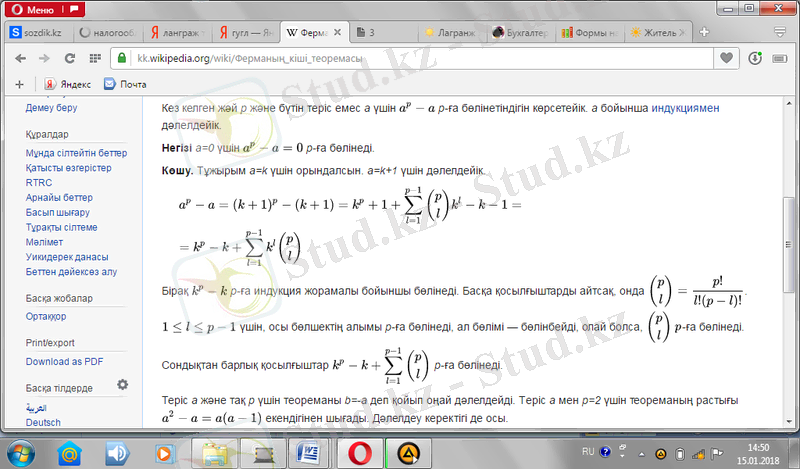p-ға бөлінеді.
Көшу. Тұжырым a=k үшін орындалсын. a=k+1 үшін дәлелдейік.

{\displaystyle =k^{p}-k+\sum _{l=1}^{p-1}k^{l}{p \choose l}}

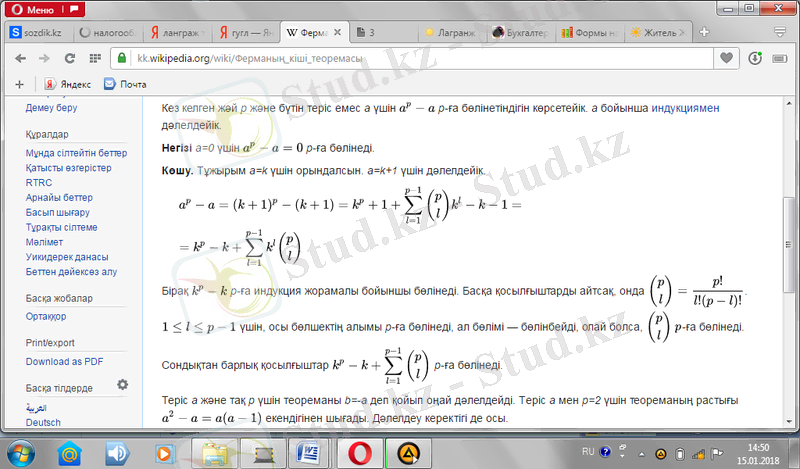
Бірақ {\displaystyle k^{p}-k} 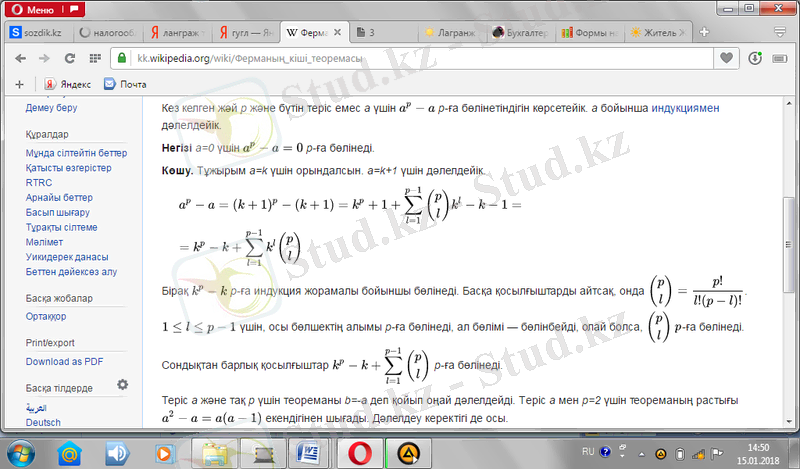p-ға индукция жорамалы бойыншы
бөлінеді. Басқа қосылғыштарды айтсақ, онда {\displaystyle {p \choose l}={p!
\over l!(p-l)!}}. {\displaystyle 1\leq l\leq p-1} үшін, осы
бөлшектің алымы p-ға бөлінеді, ал бөлімі — бөлінбейді, олай
болса, {\displaystyle {p \choose l}} {\displaystyle p}р-ға бөлінеді.
Сондықтан барлық қосылғыштар {\displaystyle k^{p}-k+\sum _{l=1}^{p-1}{p
\choose l}} p-ға бөлінеді.
Теріс a және тақ p үшін теореманы b=-a деп қойып оңай дәлелдейді.
Теріс a мен p=2 үшін теореманың растығы {\displaystyle a^{2}-a=a(a-
1)} екендігінен шығады. Дәлелдеу керектігі де осы.
Теорема жалпыламасы
• Теореманың аздаған жалпыламасы мынадай: егер p жәй сан болса,
ал m мен n —{\displaystyle m\equiv n{\pmod {p-
1}}} болатындай оң бүтін сандар болса, {\displaystyle a^{m}\equiv
a^{n}{\pmod {p}}\quad \forall a\in \mathbb {Z} }. Осы түрде
теорема ашық кілтті шифрлеу RSA жүйесінде пайдаланылады.
• Ферманың кіші теоремасы Эйлер теоремасының жекеше түрі, ал Эйлер
теоремасының өзі Кармайкл мен Лагранж теоремалар ының жекеше түрі болып
табылады.
• Ферманың кіші теоремасы шекті өрістер теориясында да жалпыламасы
бар[17].
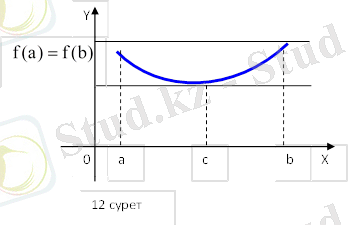
Ролль теоремасы — дифференциалдық есептеудің негізгі теоремаларының
бірі. Егер f(x) функциясы (x)(axb аралығында үзіліссіз болып, осы аралықтың
әрбір ішкі нүктесінде дифференциалданса және шеткі нүктелеріндегі мәндері
тең болса, яғни f(a)=f(b), онда (a, b) интервалында f функциясы нөлге
айналатын кем дегенде бір с нүктесі болады: ac(с)=0. Ролль теоремасын
алғаш рет 1690 ж.(b; f француз математигі М.Ролль (1652 —
1719) алгебралық көпмүшеліктер үшін тұжырымдаған.

2 Дифференциалдық есептеулердің негізгі теоремалары және оларды әр
түрлі есетерде қолдану

2.1 Ферма және Ролль теоремасы

Анықтама. 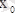нүкте 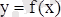 функциясының минимум (максимум) нүктесі деп
аталады, егер ол осы нүктенің 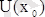төңірегінде анықталған және .
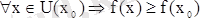Функцияның 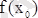мәні функция минимумы (максимумы) деп аталады.
Функцияның минимум және максимум нүктелері экстремальдық нүктелер деп
аталады, ал функцияның осы нүктелердегі мәндері экстремум мәндері деп
аталады.
кесіндісінде анықталған функцияның тек қана бір ең үлкен және ең
кіші мәндері болады, ал максимумдар және минимумдер бірнеше болуы мүмкін.
Функцияның кейбір масимумдары оның минимумдарынан кіші болуы да мүмкін (6
сурет).

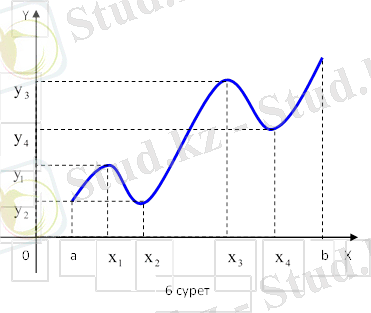
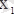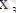Мұнда және  – максимум нүктелері, 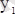 және  –
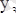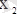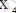максимумдер;  және – минимум нүктелері; 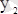және –
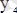минимумдер;   – экстремальдық нүктелер, – экстремумдер.
Ферма теоремасы.Айталық 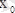– минимум нүктесі, яғни , .
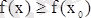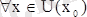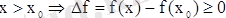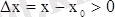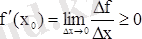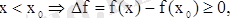
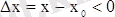Онда ,   және

.
және
.
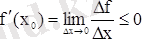Демек, .
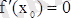Егер 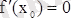онда осы нүктеде 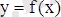функция графигіне жүргізілген
жанама өсіне параллель болады. Ферма теоремасының геометриялық
мағанасы мынада: егер экстремальдық нүктеде функция графигіне жанама бар
болса, онда ол  өсіне параллель болады (11 сурет).

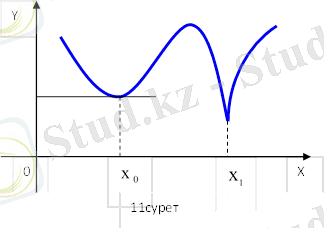
және  – минимум нүктелері, 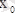нүктеде жанама 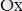өсіне
параллель, 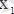 нүктеде жанама жоқ.
Ферма теоремасы
Егер (а, в) интервалында анықталған у = f (x) функциясы қайсыбір
с (а, в) нүктесінде өзінің осы аралықтағы ең үлкен (ең кіші ) мәнін
қабылдайтын болса және f ` (c) туындысы бар болса, онда f ` (c) = 0
Дәлелдеуі: f функциясы c нүктесінде ( a,b) интервалындағы ең үлкен
мәнін қабылдасын, яғни . Сонда барлық х (а, в) үшін
немесе . Бұдан мәндері үшін

Ал мәндері үшін

Теореманың шарты бойынша

шегі бар болғандықтан, ол жағдайда және жағдайда
тек бір ғана мәнді қабылдайды. Енді жағдайда (26) теңсіздікте
шекке көшіп теңсіздігін аламыз. Осылайша жағдайда да
(26`) теңсіздікте шекке көшіп, теңсіздігін аламыз. Бұл соңғы
екі теңсіздіктен шығатыны .
Геометриялық мағанасы: у = f (x) функциясы графигінің (с; f
(с)) нүктесіндегі жанамасы абцисса осіне параллель болады.
Анықтама. 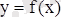функциясы 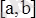кесіндісінде дифференциалданушы деп
аталады, егер ол осы кесіндіде үзіліссіз және 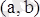интервалының барлық
нүктелерінде туындысы бар болса.
Ролль теоремасы. Айталық 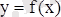функциясы 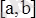кесіндісіне
дифференциалданушы және оның шеткі нүктелерінде 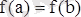 тең мәндер
қабылдасын. Онда 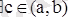 нүкте табылып .
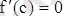Бұл теореманың геометриялық мағанасы 12 суретте көрсетілген.

Мысал. функция графигіне жүргізілген жанама 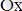өсіне параллель
болатындай нүктені (-1,1) аралығында табу мүмкін емес. Себебі Ролль
теоремасының шарты орындалмайды:  функциясы 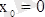 нүктеде
дифференциалданбайды, 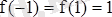шарты орындалғанмен.
Ролль теоремасы
Егер : у = f (x) функциясы:
• кесіндісінде үзіліссіз
•
• болады.
Дәлелдеуі: Теорема шарты бойынша : у = f (x) функциясы
кесіндісінде үзіліссіз, демек, Вейрштрасс теоремасы бойынша
кесіндінің қандай болса да бір нүктесінде ол өзінің ең үлкен (ең кіші)
мәнін қабылдайды.

болсын, сонда барлық үшін . Мұнда екі жағдай болуы
мүмкін:
1) m = M , онда f (x) = const демек, кез келген нүктесі үшін
, яғни теорема дұрыс.
2) Егер M m , болса , онда болғандықтан, бұл мәндерінің ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.