Тізбектер мен функциялардың шектері: анықтамалар, теоремалар және тамаша шектер


КІРІСПЕ . . .
I. ТАРАУ. ШЕКТЕР ТУРАЛЫ ТҮСІНІК. ШЕКТЕРДІҢ ҚОЛДАНЫЛУ НЕГІЗІ . . .
1. 1 Нақты сандар тізбегі жəне оның шегі . . .
1. 2 Коши және Гейне бойынша функцияның нүктедегі шегінің анықтамасы және олардың тепе-теңдігі
II. ТАРАУ. ТАМАША ШЕКТЕР . . .
2. 1 Бірінші тамаша шек . . .
2. 2 Екінші тамаша шек . . .
ҚОРЫТЫНДЫ . . .
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . .
Кіріспе
Математика - нақты өмірдегі сандық қатынастар мен кеңістіктік формалар туралы ғылым. Математикада математикалық модельдер зерттеледі. Ол нақты құбылыстардың тура математикалық модельдері болуымен қатар осы модельдерді зерттеуге арналған(структуралар) объект болуы мүмкін. Бір математикалық модель тура мазмұны жағынан бір-бірінен қашық жатқан нақты құбылыстардың қасиеттерін көрсетуі мүмкін. Мысалы, бір дифференциалдық теңдеу халықтың өсу процессін де жəне макроэкономикалық динамикасын да көрсетеді. Математика үшін қарастырылып отырған объектілердің табиғи мəні емес, олардың арасындағы қатынастардың маңызы зор. Математика жаратылыс ғылымдарында, инженер-техникалық жəнегуманитарлық зерттеулерде маңызды роль атқарады. Ол көптеген білім бөлімдерінде тек қана сандық есептеу жасау үшін ғана емес, сонымен қатар дəлірек зерттеудің тəсілі жəне ұғымдар мен проблемалардың шекті тура тұжырымдарын беру құралы болады. Адам өміріндегі əртүрлі салалардағы прогресс жетілдірілген логикалық жəне есептеу аппараты бар қазіргі замандағы математикасыз мүмкін емес. Математика қолданбалы есептерді шешуге арналған күшті құрал жəне ғылымның əмбебап тілі ғана емес, сонымен қатар ол негізгі мəдениеттің элементі де болып есептеледі. Сондықтанда математикалық білім осы заманға экономистерді фундаментальды дайындау жүйесіндегі маңызды бөлім болады. Математиканың айтылмыш тараулары, әсіресе математикалық анализ 18ғасырда одан әрі дамыды. Бұл салада ұлы математиктер Л. Эйлер мен Ж. Лагранж ерекше еңбек сіңірді. Осы ғалымдар мен француз математигі А. Лежандр еңбектерінде сандар теориясы алғаш рет жүйелі ғылым санатына қосылды. Алгебрада швейцар математигі Г. Крамер (1750) сызықтық теңдеулер жүйесін шешу үшін анықтауыштарды енгізді. Ағылшын математигі А Муавр мен Л. Эйлердің көрсеткіштік және тригонометриялық функциялардың байланысын көрсететін формулалары комплекс сандарды математикадағы қолдану өрісін кеңейте түсті. И. Ньютон, шотланд математигі Дж. Стирлинг, Л. Эйлер және П. Лаплас шектеулі айырымдарды есептеудің негізін қалады. К. Гаусс 1799 жылы алгебраның негізгі теоремасының бірінші дәлелін жариялады. Математикалық анализ әсіресе дифференциалдық теңдеулер әдістері механика мен физиканың, сондай-ақ техникалық процестердің заңдарын, математикалық өрнектеудің негізін қалады; жаратылыс тану мен техниканың ілгерілеуі осы әдістерге тікелей байланысты болды. Ағылшын математигі Б. Тейлор (1715) кез келген функцияларды дәрежелік қатарға жіктеу жөніндегі өзінің формуласын ашты. 18 ғасыр математиктері үшін қатарлар анализдің ең бір қуатты, икемді құралына айналды. Л. Эйлер, Ж. Лагранж бірінші ретті, ал Л. Эйлер, Г. Монж, П. Лаплас екінші ретті дербес туындылы дифференциалдық теңдеулердің жалпы теориясының негізін қалады.
Курстық жұмысының мақсаты:
- функцияның нүктедегі шегі, біржақты шектер, шексіздіктегі шек түсініктерін ұйғару
-ақырсыз кішкене және ақырсыз үлкен функцияларды және олардың қасиеттерін ұйғару
\
I. ТАРАУ. ШЕКТЕР ТУРАЛЫ ТҮСІНІК. ШЕКТЕРДІҢ ҚОЛДАНЫЛУ НЕГІЗІ
1. 1 Нақты сандар тізбегі жəне оның шегі
Анықтама 1. 1. Әрбір n натурал санға сәйкесінше a n нақты сан сәйкестендірілсін ( түрлі n натурал сан ретінде сәйкестендірілген бірдей сан да болуы мүмкін) . a n , элементтер жиынтығын n=1, 2, … сандық тізбек деп атайды; әрбір a n элементі осы тізбектің элементі (немесе мүшесі) деп аталады, n саны - оның нөмірі. Қысқаша {a n } символымен белгіленеді
Анықтама 1. 2.
,
Егер
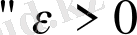
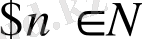 ,
үшін,
,
үшін,
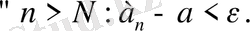 орындалса, онда а саны {a
n
} тізбегінің шегі деп аталады Белгіленуі
орындалса, онда а саны {a
n
} тізбегінің шегі деп аталады Белгіленуі
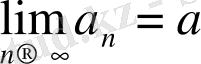 немесе a
n
→ a, n → ∞. болғанда. . Шегі бар тізбек жинақталатын деп аталады. . Кері жағдайда жинақталмайтын тізбек
немесе a
n
→ a, n → ∞. болғанда. . Шегі бар тізбек жинақталатын деп аталады. . Кері жағдайда жинақталмайтын тізбек
│ a n - а│< ε пара-пар а -ε < a n < a+ε
Анықтама 1. 2
Егер тізбектің кез келген маңайына тізбектің кейбір мүшелерінен басқа барлық мүшелері тиісті болса, онда а саны {a
n
} тізбегінің шегі деп аталады (яғни
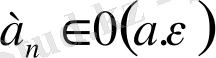 ) .
) .
Теорема 1. 1. Жинақталатын тізбектің шегі жалғыз болады
Дәлелдеуі: Кері жоримыз. n→ ∞ болсын
a n → a, a n → b, мұндағы a < b.
a
n
→ a
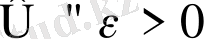
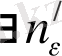
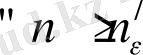 :
:
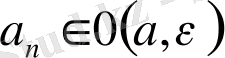
a
n
→ b
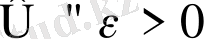
 :
:
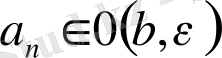
0 (a, ε)
және
0 (b, ε)
қиылыспайтындай етіп
ε > 0
таңдап аламыз, мысалы
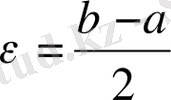 ;
;
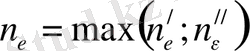 болсын
,
онда
болсын
,
онда
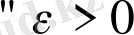
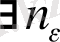
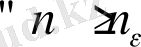 :
:
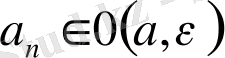 және
және
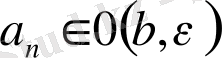 ,
бұл мүмкін емес, себебі бұл маңайлар қиылыспайды.
,
бұл мүмкін емес, себебі бұл маңайлар қиылыспайды.
Қарама-қайшылық теореманы дәлеледейді.
Теңсіздіктер мен шектің байланысы.
1. Егер a
n
≤ b
n
≤ c
n
, n = 1, 2, … және
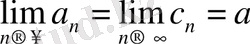 , онда
, онда
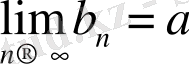
2. Егер
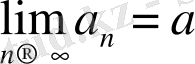 және
және
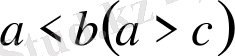 , онда
, онда
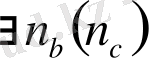
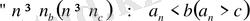
3. Егер
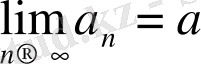 және
және
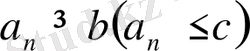 , n = 1, 2, …, онда a ≥ b (a ≤ c)
, n = 1, 2, …, онда a ≥ b (a ≤ c)
2. Монотонды тізбектің шегі
Анықтама 2. 1.
{a
n
} тізбегі жоғарыдан(төменнен) шенелген деп аталады, егер
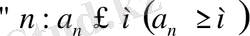 болатындай
болатындай
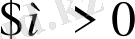 .
.
Анықтама 2. 2.
Жоғарыдан және төменнен шенелген тізбек шекнелген деп аталады. {a
n
}-шенелген егер
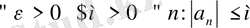 болса.
болса.
Теорема 2. 1. (тізбектің жинақталуының қажетті шарты)
Жинақталатын тізбек шенелген тізбек болады
Анықтама 2. 3. а саны а n тізбегінің дәл жоғарғы(төменгі) шені деп аталады (белгіленуі : а = sup{a n } (a = inf {a n }), егер:
1)
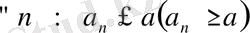
2)
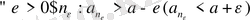
Анықтама 2. 4.
Егер
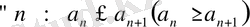 болса, онда {a
n
} тізбегі өспейтін (кемімейтін) деп аталады.
болса, онда {a
n
} тізбегі өспейтін (кемімейтін) деп аталады.
Өспейтін және кемімейтін тізбектер монотонды(бірсарынды) тізбектер деп аталады.
Теорема 2. 2.
Ж
оғарыдан (төменнен) шенелген кемімейтін(өспейтін) {a
n
} тізбегнің шегі бар, және
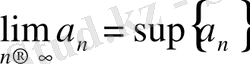 (
(
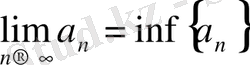 ) .
) .
Салдар . Кемімейтін тізбек жинақталу үшін оның жоғарыдан шенелуі қажетті және жеткілікті.
Мысал:
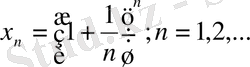
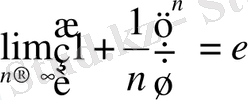 екенін көрсету керек(е≈2, 718…) С. Ө. Ж
екенін көрсету керек(е≈2, 718…) С. Ө. Ж
3. Больцано - Вейерштрасс теоремасы және Коши критериі
Анықтама3. 1
. Егер
b
k,,
k=1, 2, …тізбегі үшін
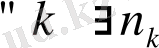 : b
k
=a
nk
, мұндағы n
k1 <
n
k2
, сонда тек сонда ғана к
1
<к
2.,
онда b
k,,
k=1, 2, …тізбегі
: b
k
=a
nk
, мұндағы n
k1 <
n
k2
, сонда тек сонда ғана к
1
<к
2.,
онда b
k,,
k=1, 2, …тізбегі
 {a
n
} тізбегінің тізбекшесі деп аталады.
{a
n
} тізбегінің тізбекшесі деп аталады.
, Теорема 3. 1. (Больцано- Вейерштрасс) Кез келген шенелген тізбектен жинақталатын тізбкше бөліп алуға болады.
Анықтама3. 2.
Егер
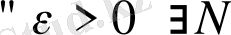
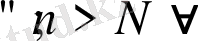 р натурал саны үшін \ х
п
- х
n+p
\ < ε теңсіздігі орындалса, {х
n
} тізбегі фундаменталды деп аталады
р натурал саны үшін \ х
п
- х
n+p
\ < ε теңсіздігі орындалса, {х
n
} тізбегі фундаменталды деп аталады
Бұл анықтама келесіге эквивалентті.
Анықтама 3. 3.
Егер
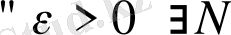
 және
және
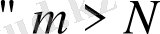 үшін
үшін
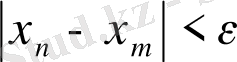 теңсіздігі орындалса, {х
n
} тізбегі фундаменталды (іргелі) деп аталады.
теңсіздігі орындалса, {х
n
} тізбегі фундаменталды (іргелі) деп аталады.
Бұл анықтамалардың геометриялық мағынасы келесіде жатыр: егер {
x
n
} тізбегі - фундаменталды болса,
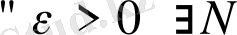 үшін нөмірі
N
-нен үлкен болатын тізбектің екі мүшесінің арасы ε-нан кіші болады.
үшін нөмірі
N
-нен үлкен болатын тізбектің екі мүшесінің арасы ε-нан кіші болады.
Теорема 3. 2. (тізбектің жинақтылығының Коши критериі ) . Тізбек жинақталу үшін оның фундаменталы (іргелі) болуы қажетті және жеткілікті.
Ақырсыз кішкене және ақырсыз үлкен тізбектер
Анықтама4. 1
. Е
гер
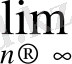 x
n
=0 орындалса, онда { х
n
} ақырсыз кішкене тізбек деп аталады
x
n
=0 орындалса, онда { х
n
} ақырсыз кішкене тізбек деп аталады
Анықтама4. 2.
Егер
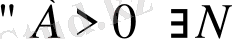 үшін
үшін
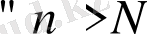 : \х
п
\>А болса, онда {х
n
} ақырсыз үлкен тізбек деп аталады.
: \х
п
\>А болса, онда {х
n
} ақырсыз үлкен тізбек деп аталады.
Геометриялық тұрғыдан бұл нөлдің кез келген маңайында тізбектің тек ақырлы мүшелері ғана болады, ал одан тыс - шексіз көп мүшелер тиісті болады.
Егер {
х
п
} тізбегі -ақырсыз үлкен болса, онда
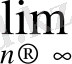 x
n
=
x
n
=
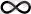 деп жазылады. Егер ақырсыз үлкен тізбектің барлық мүшелерінің нөмірі оң(теріс) болса, онда
деп жазылады. Егер ақырсыз үлкен тізбектің барлық мүшелерінің нөмірі оң(теріс) болса, онда
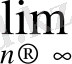 х
п
= + ∞(- ∞)
деп жазылады. Ақырсыз үлкен тізбек жинақталмайды және
х
п
= + ∞(- ∞)
деп жазылады. Ақырсыз үлкен тізбек жинақталмайды және
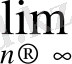 х
п
= + ∞(- ∞)
жазуы тек {х
п
} тізбегінің ақырсыз үлкен екенін білдіреді.
х
п
= + ∞(- ∞)
жазуы тек {х
п
} тізбегінің ақырсыз үлкен екенін білдіреді.
Кез келген ақырсыз үлкен тізбек шектелмеген болады. Керісі дұрыс емес: шенелмеген тізбек ақырсыз үкен болмауы да мүмкін.
Теорема 4. 1. Ақырсыз кішкене тізбектердің ақырлы санының алгебралық қосыныдысы ақырсыз кішкене тізбек болып табылады
Теорема 4. 2. Ақырсыз үлкен тізбектің шенелген тізбекке көбейтіндісі ақырсыз кішкене тізбек болып табылады
Салдар. Ақырсыз кішкене шаманың ақырғы санының көбейтіндісі ақырсыз кішкене шама болады.
Теорема 4. 3.
Егер {х
п
} тізбегі - ақырсыз үлкен болса, онда қандай да бір п нөмірінен бастап {1/х
n
} тізбегі анықталған және ақырсыз кішкене тізбек болады. Егер {х
п
} тізбегі - ақырсыз кішкене
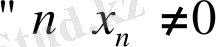 болса, онда {1/х
п
} тізбегі ақырсыз үлкен болады.
болса, онда {1/х
п
} тізбегі ақырсыз үлкен болады.
Дәлелдеуі(теорема 4. 1) :
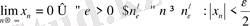 болсын
болсын
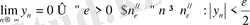
n
ε
= max (n
ε
', n
ε
'')
деп алып, онда
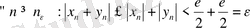 яғни
.
яғни
.
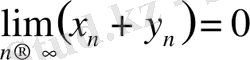 .
.
Математикалық индукция әдісі бойынша ақырсыз кішкене шамалардың ақырлы саны үшін дұрыстық дәлеледенеді.
1. 2 Коши және Гейне бойынша функцияның нүктедегі шегінің анықтамасы және олардың тепе-теңдігі
x
- сандық айнымалы,
Х
- оның өзгеру облысы болсын. Егер әрбір
x
 санына қандай да бір
у
саны сәйкесінше қойылса, онда
Х
жиынында функция анықталады деп айтады да,
y =f(x)
деп жазады. Х жиынын -
f(x) функциясының анықталу облысы
,
х
-
тәуелсіз айнымалы
(немесе функция аргументі), ал
х
айнымалысының мәніне сейкес келетін у саны - функциядағы
х
нүктесіндегі дербес мәні деп аталады. Функцияның Y сәйкестігінің барлық дербес мәндер жиыны-
f(x) функциясының мәндер жиыны
деп аталады.
санына қандай да бір
у
саны сәйкесінше қойылса, онда
Х
жиынында функция анықталады деп айтады да,
y =f(x)
деп жазады. Х жиынын -
f(x) функциясының анықталу облысы
,
х
-
тәуелсіз айнымалы
(немесе функция аргументі), ал
х
айнымалысының мәніне сейкес келетін у саны - функциядағы
х
нүктесіндегі дербес мәні деп аталады. Функцияның Y сәйкестігінің барлық дербес мәндер жиыны-
f(x) функциясының мәндер жиыны
деп аталады.
Егер
а
нүктесінің кез келген маңайында
Х
жиынының
а-
дан айрықша нүктелері бар болса, онда
а
(
 немесе
немесе
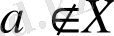 ) нүктесі
Х
жиынының шектік нүктесі деп аталады.
) нүктесі
Х
жиынының шектік нүктесі деп аталады.
Бұл тақырыптағы анықтамаларында, f(x) функциясының анықталу облысы Х жиынының а шектік нүктесі деп болжаймыз.
Анықтама1. 1. (Коши бойынша) .
Егер
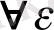 >0 санына сәйкес
>0 санына сәйкес
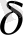 >0 табылып,
>0 табылып,
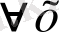 үшін
үшін
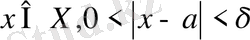 шарттарын қанағаттандыратын
шарттарын қанағаттандыратын
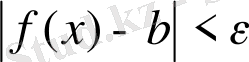 теңсіздігі орындалса, онда
b
санын
f(x) функциясының а нүктесіндегі (
теңсіздігі орындалса, онда
b
санын
f(x) функциясының а нүктесіндегі (
 ұмтылғанда) шегі деп аталады
ұмтылғанда) шегі деп аталады
Анықтама 1. 2. (Гейне бойынша) .
Егер
а санына жинақты кез келген
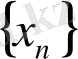 тізбегі мұның әрбір элементі
тізбегі мұның әрбір элементі
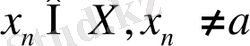 үшін
функция мәндерінің сәйкес
үшін
функция мәндерінің сәйкес
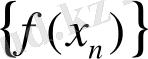 тізбегі
b санына жинақты болса, онда
b
санын
f(x) функцияның а нүктесіндегі шегі деп атайды.
тізбегі
b санына жинақты болса, онда
b
санын
f(x) функцияның а нүктесіндегі шегі деп атайды.
Белгіленуі:
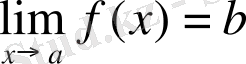 немесе
немесе
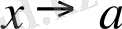 жағдайда
жағдайда
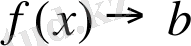
Ескерту:
а
нүктесіндегі функцияның шегі, тек функцияның анықталу облысындағы
а
шектік нүктелері үшін енгізіледі. Айтып өтерлік, функция а нүктесінде анықталмауы да мүмкін, яғни жалпылағанда
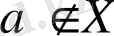 .
.
Осы 2 анықтаманы теріске шығарайық.
1. 1. Анықтаманың терістеуі.
Егер
 саны табылып,
саны табылып,
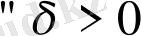 саны үшін
саны үшін
 нүктесін табуға болса және
нүктесін табуға болса және
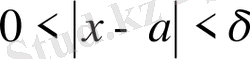 теңсіздігі орындалғанда
теңсіздігі орындалғанда
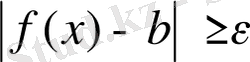 теңсіздігі орындалса, онда
b санын
f(x)
функциясының
а
[
теңсіздігі орындалса, онда
b санын
f(x)
функциясының
а
[
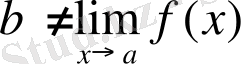 ]
нүктесіндегі шегі болмайды
]
нүктесіндегі шегі болмайды
1. 2. Анықтаманың терістеуі.
Егер а санына жинақты
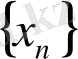
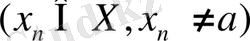 тізбегі бар болып, сәйкес
тізбегі бар болып, сәйкес
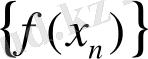 тізбегі b санына жинақталмаса, онда
тізбегі b санына жинақталмаса, онда
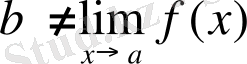 болады
болады
Теорема 1. 1. . Функцияның шегі 1. 1 және 1. 2 анықтамалары эквивалентті
Функцияның шегі туралы теоремы. Күрделі функцияның шегі. Бір жақты шектер
Теорема 2. 1
.
f(x) және g(x) функциялары а нүктесінің қандай да бір маңайында (а нүктесінде анықталмауы да мүмкін) анықталсын және
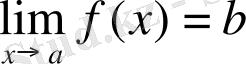 ,
,
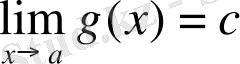 орындалсын.
орындалсын.
Онда:
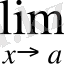 (f(x) +g(x) ) =b + c;
(f(x) +g(x) ) =b + c;
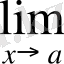 (f(x) -g(x) ) =b - c;
(f(x) -g(x) ) =b - c;
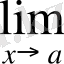 f(x) g(x) =bc
;
f(x) g(x) =bc
;
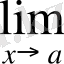
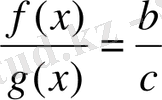
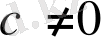 болғанда.
болғанда.
Теорема 2. 2
.
f(x)
 g(x)
g(x)
 h(x) теңсіздіктерін қанағаттандыратын f(x), g(x) және h(x) ) функциялары а нүктесінің қандай да бір маңайында анықталсын, тек а нүктесінде анықталмауы мүмкін және
h(x) теңсіздіктерін қанағаттандыратын f(x), g(x) және h(x) ) функциялары а нүктесінің қандай да бір маңайында анықталсын, тек а нүктесінде анықталмауы мүмкін және
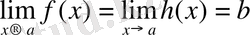 орындалса
,
онда
орындалса
,
онда
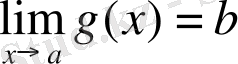 .
.
Теорема 2. 3 . Егер f(x) функциясының а нүктесінде шегі бар болса, онда а нүктесінің маңайы табылып, осы маңайда (а нүктесі тиісті болмауы мүмкін) функция шенелген болады.
Теорема 2. 4
.
Егер
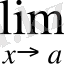 f(x) =b
f(x) =b
 0 бар болса, онда а нүктесінің маңайы бар болып, осы маңайындағы функциясының таңбасы b санының таңбасындай болады.
0 бар болса, онда а нүктесінің маңайы бар болып, осы маңайындағы функциясының таңбасы b санының таңбасындай болады.
Теорема 2. 5. ( күрделі функциясының шегі туралы ) .
D облысында
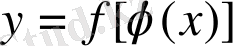 күрделі функцияның мағынасы бар болсын. Егер:
күрделі функцияның мағынасы бар болсын. Егер:
1
. Кез келген
 үшін
үшін
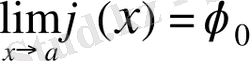 және
және
 ;
;
2.
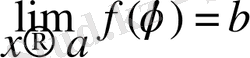 ;
;
онда
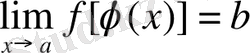 күрделі функцияның шегі бар болады.
күрделі функцияның шегі бар болады.
Ескерту
: Тұжырымды келесі түрде жазуға болады мына
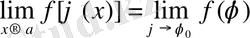 , егер
, егер
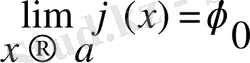 бұл формуланы күрделі функцияның шегін алмастыру арқылы есептеу деп атайды
бұл формуланы күрделі функцияның шегін алмастыру арқылы есептеу деп атайды
Бір жақты шектер
Анықтама 2. 1. (Коши бойынша) .
Егер
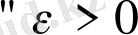 үшін оған тәуелді
үшін оған тәуелді
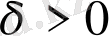 саны табылып,
саны табылып,
 а< x < a+
а< x < a+
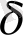 ( а-
( а-
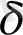 < x < a)
теңсіздігін қанағаттандыратын
< x < a)
теңсіздігін қанағаттандыратын
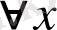 үшін
үшін
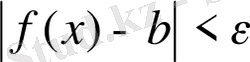 теңсіздігі орындалса, онда
b
саны
а
нүктесіндегі
f(x)
функциясының оң (сол) жақты шегі деп аталады.
теңсіздігі орындалса, онда
b
саны
а
нүктесіндегі
f(x)
функциясының оң (сол) жақты шегі деп аталады.
Анықтама2. 2. (Гейне бойынша) .
Егер
а
санына жинақты кез келген
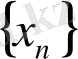 тізбегі үшін, мұндағы
тізбегі үшін, мұндағы
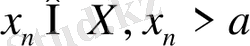 (
(
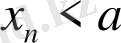 ),
мәндерінің сәйкес
),
мәндерінің сәйкес
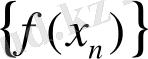 тізбегі
b
санына жинақты болса, онда
b
саны
а
нүктесіндегі
f(x)
функциясының оң (сол) жақты шегі деп аталады.
тізбегі
b
санына жинақты болса, онда
b
саны
а
нүктесіндегі
f(x)
функциясының оң (сол) жақты шегі деп аталады.
Белгіленуі:
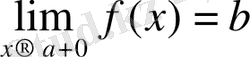 немесе
f(a+0) =b
(сәйкесінше
немесе
f(a+0) =b
(сәйкесінше
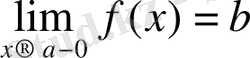 немесе
f(a-0) =b) .
немесе
f(a-0) =b) .
2. 1 және 2. 2 анықтамалары эквивалентті.
Теорема 2. 6.
Егер f(a+0) және f(a-0) бар болса және f(a+0) =f(a-0) =b опындалса, онда
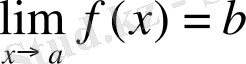 бар болады.
бар болады.
Теорема 2. 7
.
Егер f(x) функциялары а нүктесіндегі қандайда бір маңайында анықталса, тек а нүктенің өзінде анықталмауы мүмкін және
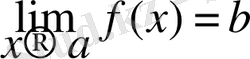 бар болса, онда f(a+0) и f(a-0) бар болады, сонымен қатар f(a+0) =f(a-0) =b теңдігі орындалады .
бар болса, онда f(a+0) и f(a-0) бар болады, сонымен қатар f(a+0) =f(a-0) =b теңдігі орындалады .
Шексіздіктегі шек. Ақырсыз үлкен функциялар.
f(x) функциясы ( с, +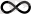 ) аралығында анықталған болсын.
) аралығында анықталған болсын.
Анықтама3. 1. (Коши бойынша) .
Егер
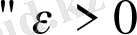 үшін
үшін
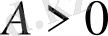 (
(
 ) саны табылып,
) саны табылып,
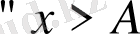 мәндері үшін
мәндері үшін
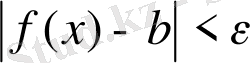 (1) теңсіздігі орындалса, онда b саны
(1) теңсіздігі орындалса, онда b саны
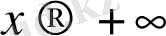
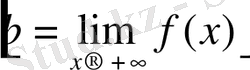 ұмтылғанда f(x) функцияның шегі деп аталады.
ұмтылғанда f(x) функцияның шегі деп аталады.
Анықтама3. 2. (Гейне бойынша) .
Егер кез келген ақырсыз үлкен
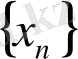 (x
n.
>c ) тізбегі үшін сәйкес
(x
n.
>c ) тізбегі үшін сәйкес
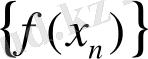 функция мәнінің тізбегі b санына жинақты болса, онда b=
функция мәнінің тізбегі b санына жинақты болса, онда b=
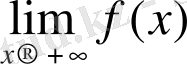 тең болады.
тең болады.
3. 1 және 3. 2 анықтамалары эквивалентті.
Сәйкесінше
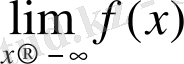 анықталады
.
Егер
анықталады
.
Егер
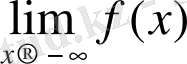 =
=
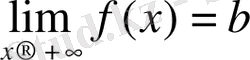 болса, онда
болса, онда
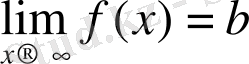 деп жазады. Мысалы,
деп жазады. Мысалы,
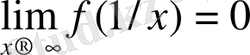 .
.
 ұмтылғандағы шектер үшін, 2. 1 теоремасына ұқсас теоремалар орындалады.
ұмтылғандағы шектер үшін, 2. 1 теоремасына ұқсас теоремалар орындалады.
Анықтама 3. 3.
Егер

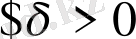 бар болып,
бар болып,
 ,
,
 , а< x < a+
, а< x < a+
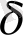 үшін
үшін
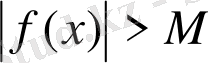 теңсіздігі орындалса, онда f(x) функциясы а нүктесінде оң жақтан ақырсыз үлкен деп аталады. Егер 3. 1. анықтамасындағы (1) теңсіздігінің орнында f(x) >М (f(x) <-M), теңсіздігі орындалса, онда а нүктесінде оң жақтан ақырсыз үлкен плюс (минус) таңбасымен f(x) функциясы болып табылатынын түсініледі, және
теңсіздігі орындалса, онда f(x) функциясы а нүктесінде оң жақтан ақырсыз үлкен деп аталады. Егер 3. 1. анықтамасындағы (1) теңсіздігінің орнында f(x) >М (f(x) <-M), теңсіздігі орындалса, онда а нүктесінде оң жақтан ақырсыз үлкен плюс (минус) таңбасымен f(x) функциясы болып табылатынын түсініледі, және
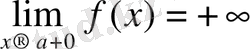 немесе f(а+0) =
немесе f(а+0) =
 (сәйкесінше
(сәйкесінше
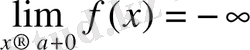 и f(а+0) =
и f(а+0) =
 ) деп жазылады.
) деп жазылады.
Жоғарыдағыға ұқсас
а
нүктесінде сол жақтан ақырсыз үлкен функция анықталады. Егер
а
нүктесінде оң жақтан және сол жақтан функция ақырсыз үлкен болып табылса, онда
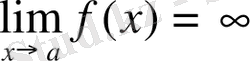 деп жазылады
.
Мысалы,
деп жазылады
.
Мысалы,
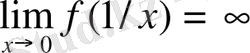 .
.
Анықтама 3. 4.
Егер а санына жинақты кез келген
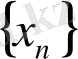 , мұндағы
, мұндағы
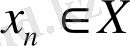 ,
,
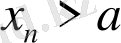 (
(
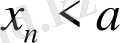 ), тізбегіне сәйкес
), тізбегіне сәйкес
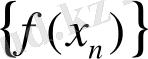 тізбегі ақырсыз үлкен болып табылса, онда f(x) функциясы а нүктесінің сол (оң) жағындағы ақырсыз үлкен функциясы деп аталады.
тізбегі ақырсыз үлкен болып табылса, онда f(x) функциясы а нүктесінің сол (оң) жағындағы ақырсыз үлкен функциясы деп аталады.
3. 1 және 3. 2 анықтамалары эквивалентті.
f(x) функциясы (с, +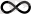 ) сәулесінде анықталатын болсын.
) сәулесінде анықталатын болсын.
Анықтама3. 5.
Егер

 (А
(А
 с ), мұндағы
с ), мұндағы
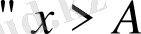 :
:
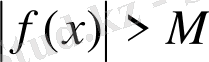 , онда
, онда
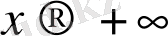 ұмтылғанда f(x) функциясын ақырсыз үлкен деп аталады.
ұмтылғанда f(x) функциясын ақырсыз үлкен деп аталады.
Анықтама 3. 6.
Егер кез келген ақырсыз үлкен
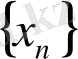 (х
n
>c ) тізбегі үшін сәйкес
(х
n
>c ) тізбегі үшін сәйкес
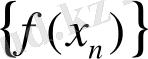 тізбегі ақырсыз үлкен болса, онда
тізбегі ақырсыз үлкен болса, онда
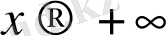 ұмтылғанда f(x) функциясы ақырсыз үлкен деп аталады.
ұмтылғанда f(x) функциясы ақырсыз үлкен деп аталады.
Белгіленуі:
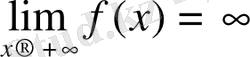 .
.
3. 5 және 3. 6 анықтамалары эквивалентті.
Сәйкесінше
 ұмтылғанда:
ұмтылғанда:
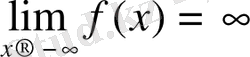 ақырсыз үлкен функция түсінігі енгізіледі. Егер
ақырсыз үлкен функция түсінігі енгізіледі. Егер
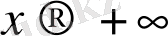 және
және
 ұмтылғанда
f(x)
функциясы ақырсыз үлкен болса, онда
ұмтылғанда
f(x)
функциясы ақырсыз үлкен болса, онда
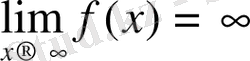 деп жазылады
.
деп жазылады
.
Мысалы
,
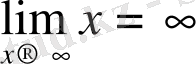 .
.
Ақырсыз кішкене функциялар. Ақырсыз кішкене функцияларды салыстыру
Егер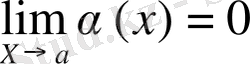 болса, онда
болса, онда
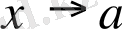 ( а нүктесіне) ұмтылғанда
( а нүктесіне) ұмтылғанда
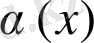 функциясын ақырсыз кішкене деп атайды. Айталық,
функциясын ақырсыз кішкене деп атайды. Айталық,
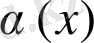 және
және
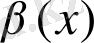 - функциялары
- функциялары
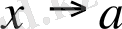 жағдайда ақырсыз кішкене функциялар.
жағдайда ақырсыз кішкене функциялар.
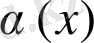 және
және
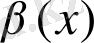 функциялары үшін келесі шарттар орындалса, онда олар:
функциялары үшін келесі шарттар орындалса, онда олар:
а) Егер
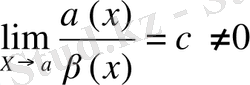
болса, онда
 (
а нүктесіне
) ұмтылған жағдайында реті бірдей ақырсыз кішкене функциялар деп атайды.
(
а нүктесіне
) ұмтылған жағдайында реті бірдей ақырсыз кішкене функциялар деп атайды.
б) Егер
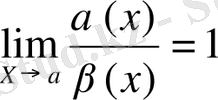 (
(
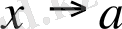 жағдайында
жағдайында
 ~
~
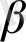 белгіленеді)
белгіленеді)
болса, онда
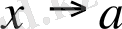 (
а нүктесіне
) ұмтылған жағдайында
эквивалентті ақырсыз кішкене функциялар
деп атайды
.
(
а нүктесіне
) ұмтылған жағдайында
эквивалентті ақырсыз кішкене функциялар
деп атайды
.
в
)
Егер
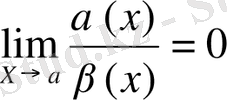 болса, онда
болса, онда
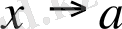 (
а нүктесіне
) ұмтылған жағдайында
(
а нүктесіне
) ұмтылған жағдайында
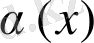 функциясын
функциясын
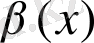 функциясына
қарағанда реті жоғары ақырсыз кішкене функциясы деп атайды және
функциясына
қарағанда реті жоғары ақырсыз кішкене функциясы деп атайды және
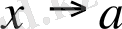 (
(
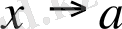 жағдайда
жағдайда
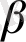 -дан «о аз»
-дан «о аз»
 тең болады) жағдайында
тең болады) жағдайында
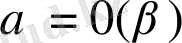 деп белгілейді.
деп белгілейді.
Мысалы
,
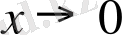 жағдайында
х
2
=о(х)
болады .
жағдайында
х
2
=о(х)
болады .
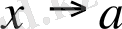 +0,
+0,
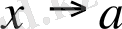 - 0,
- 0,
 жағдайлары үшін, сәйкесінше анықтамаларының орны бар.
жағдайлары үшін, сәйкесінше анықтамаларының орны бар.
«о аз» белгісі бар теңсіздігі, шартты болып табылатынын ескеру керек. Мысалы,
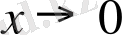 жағдайында
х
2
=0(х)
теңдігі дұрыс, бірақ о(х) =х
2
теңдігі дұрыс емес, өйткені о(х) белгісі белгілі бір функцияны емес, кез келген функцияны білдіреді, ол
жағдайында
х
2
=0(х)
теңдігі дұрыс, бірақ о(х) =х
2
теңдігі дұрыс емес, өйткені о(х) белгісі белгілі бір функцияны емес, кез келген функцияны білдіреді, ол
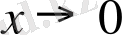 жағдайында
х
- тен гөрі реті жоғары ақырсыз кішкене функция. Ондай функциялар ақырсыз көп: дербес жағдайда кез келген
х
р
(мұндағы р>1)
функциясы
жағдайында
х
- тен гөрі реті жоғары ақырсыз кішкене функция. Ондай функциялар ақырсыз көп: дербес жағдайда кез келген
х
р
(мұндағы р>1)
функциясы
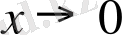 жағдайында о(х) болып табылады. Егер
жағдайында о(х) болып табылады. Егер
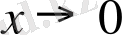 жағдайында
х
2
=о(х)
теңдігі болса, онда
жағдайында
х
2
=о(х)
теңдігі болса, онда
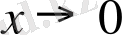 жағдайында
x
2
функциясын
х
функциясына қарағанда реті жоғары ақырсыз кішкене функциялардың жиынына тиісті болады. Сондықтан «кері жағында»
(о(х) =х
2
)
теңдігі дұрыс емес:
о(х)
функцияның барлық жиындары жалғыз
х
2
функциясына жинақталмайды.
жағдайында
x
2
функциясын
х
функциясына қарағанда реті жоғары ақырсыз кішкене функциялардың жиынына тиісті болады. Сондықтан «кері жағында»
(о(х) =х
2
)
теңдігі дұрыс емес:
о(х)
функцияның барлық жиындары жалғыз
х
2
функциясына жинақталмайды.
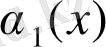 және
және
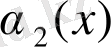 - функциялары
- функциялары
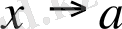 жағдайда еркін ақырсыз кішкене функциялар, мұндағы
жағдайда еркін ақырсыз кішкене функциялар, мұндағы
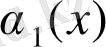 =
=
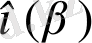 және
және
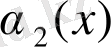 =
=
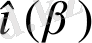 .
.
Онда
жағдайында
+
=
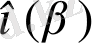
Бұл теореманы қысқаша түрінде жазып алуға болады:
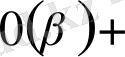
=
.
«
о аз»
белгісінің тағы бір қатар қасиеттерін көрстейік (
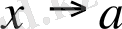 жағдайда
жағдайда
 және
және
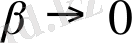 ) .
) .
1
0
.
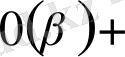
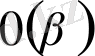 =
=
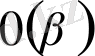
2
0
.
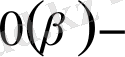
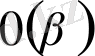 =
=
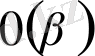 .
.
3
0
. 0(
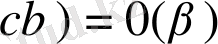
 сан
сан
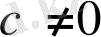 .
.
4
0
.
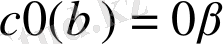

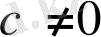 .
.
5
0
.
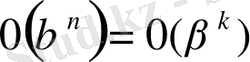
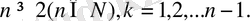
6
0
.
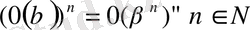 .
.
7
0
.
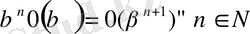
8
0
.
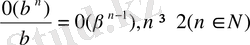 .
.
Кез келген ақырсыз кішкене функцияны
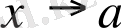 жағдайында о(1) белгісімен белгілейік. Онда n=1 болғанда да 8
0
қасиеті орынды болады:
жағдайында о(1) белгісімен белгілейік. Онда n=1 болғанда да 8
0
қасиеті орынды болады:
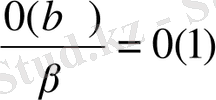 .
.
9
0
.
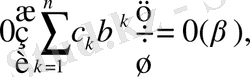 мұндағы
мұндағы
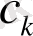 -сан
.
-сан
.
10
0
.
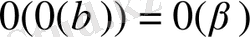 .
.
11
0
.
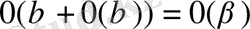 .
.
12
0
.
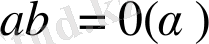 и
и
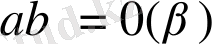 .
.
13
0
. Егер
 ~
~
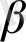 , онда
, онда
 -
-
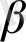 =о(
=о(
 ) және
) және
 -
-
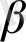 =о(
=о(
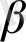 ) .
) .
Функияның шегін тапқан кезде келесі 4. 2 теореманы қолданған орынды болады:
Теорема 4. 2.
Айталық
,
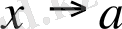 жағдайда
жағдайда
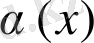 ,
,
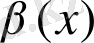 ,
,
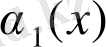 ,
,
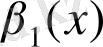 - ақырсыз кішкене функциялар және
- ақырсыз кішкене функциялар және
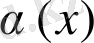 ~
~
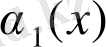 ;
;
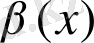 ~
~
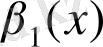 болса, онда
болса, онда
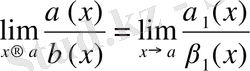 болады.
болады.
Ескерту:
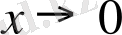 жағдайда sin
kx
~
kx
; arcsin
kx
~
kx;
tg
kx
~
kx
; arctg
kx
~
kx
; ln(1+
kx
) ~
kx
.
жағдайда sin
kx
~
kx
; arcsin
kx
~
kx;
tg
kx
~
kx
; arctg
kx
~
kx
; ln(1+
kx
) ~
kx
.
Монотонды (бірсарынды) функциялардың шегі
Теорема 5. 1 . (монотонды функциялардың шегі туралы) : Егер y=f (x) функциясы (a, b) интервалында монотонды өспелі болса, онда a және b нүктелеріндегі y=f (x) функциясының бір жақты шектері (ақырлы немесе ақырсыз) бар болады және келесі теңдіктер орындалады:
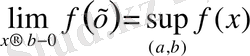 ;
;
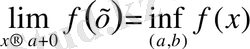
Егер y=f (x) функциясы (a, b) интервалында монотонды кемімелі болса, онда шектері (ақырлы немесе ақырсыз) бар болады және келесі теңдіктер орындалады.
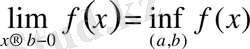 ;
;
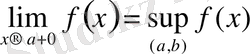 .
.
Дәлелдеуі
: Айталық
y=f (x)
функциясы (a, b) интервалында монотонды кемімелі болсын. Егер А=
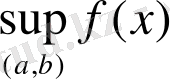 болса, онда
болса, онда
1)
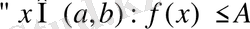
2)
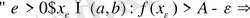
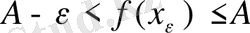
Функция монотонды өспелі, сондықтан
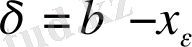 деп болжасақ, онда
деп болжасақ, онда
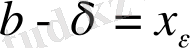 <
x
<b
<
x
<b
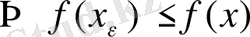 теңсіздігі орындалады.
теңсіздігі орындалады.
Сонымен
x
үшін:
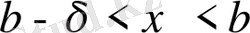 келесі теңсіздік орындалады:
келесі теңсіздік орындалады:
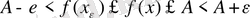 ,
,
мұндағы
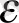 - кез келген оң сан,
- кез келген оң сан,
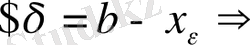 :
:
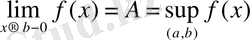 :
:
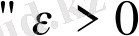
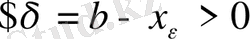 , яғни
, яғни
 :
:
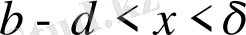 :
:
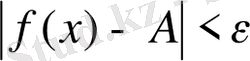 .
.
Егер
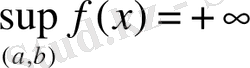 болса, онда
болса, онда
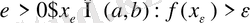 .
.
Айталық,
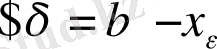
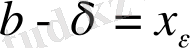 <x<b болса, f-монотонды функция болғандықтан
<x<b болса, f-монотонды функция болғандықтан
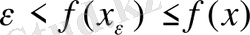
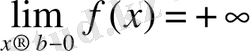 . Онда:
. Онда:
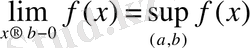
II. ТАРАУ. ТАМАША ШЕКТЕР
2. 1 Тамаша шектер
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz