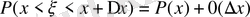Ықтималдық теориясы мен комбинаторика: 1-8 дәрістік силлабус


1-БӨЛІМ. ДӘРІС КЕШЕНІ
1 - дәріс. Ықтимал теориясы туралы
Сабақтың мақсаты: Ықтимал теорисы деген не екенін түсіндіру
Дәрістің жоспары:
- Ең анық, мүмкін емес, кездейсоқ оқиғалардың анықтамалары. Оқиға деген не?
- Ықтимал пәнінің анықтамасы.
- Кездейсоқ оқиғалардың түрлері жалғыз ғана мүмкіндікті, тең мүмкіндікті оқиғалар.
- Ықтимал теориясының қолданылуы. Тарихи мәлімдеме
1. Ең анық, мүмкін емес, кездейсоқ оқиғалардың анықтамалары. Оқиға деген не.
Анықтама: Ең анық оқиға дегеніміз оқиға орындалуы міндетті түрде болуы керек, егер белгілі шарттар жиынтығы S орындалса.
Анықтама: Кездейсоқ оқиға дегеніміз оқиға болуы да, болмауы да мүмкін.
Анықтама: Мүмкін емес оқиға деп оқиға орындалуы мүмкін емес, егер белгілі шарттар жиынтығы S орындалса.
2. Ықтимал пәнінің анықтамасы.
Анықтама: Біртектес топтасқан, кез келген оқиғалардың ықтималдық заңдылықтарын зерттейтін ғылымды ықтимал пәнінің теориясы дейді.
3 . Кездейсоқ оқиғалардың түрлері.
Анықтама: Кездейсоқ оқиға дегеніміз оқиға болуы да, болмауы да мүмкін.
Кездейсоқ оқиғалар үйлесімді, үйлесімсіз, жалғыз ғана мүмкіндікті және тең мүмкіндікті болып, бөлінеді. Егер тәжірибе нәтижесінде бір оқиғаның пайда болуы қалған оқиғалардың пайда болуына кедергі жасамаса, онда мұндай оқиғаларды үйлесімді оқиғаларды деп атайды.
4. Ықтималдықтар теориясының қолданылуы. Тарихи мәлімдеме.
Ықтимал теориясының әдістерін беріктілік теориясында, теориялық физикада, геодезияда, астрономияда, атыс теориясында, автоматты басқару теориясында, жалпы байланыс теориясында қолданады. Ықтималдықтар теориясы - математиканың қолданбалы және статистикалық негіздерін дәлелдеу үшін қолданылатын ғылым. Оны өндірісті жоспарлау және ұйымдастыру үшін, технологиялық процестерді бақылау үшін, өнімнің сапасын тексеру үшін, ескерту және теорисының дамуына байланысты оның техникада, химияда, экономикада қолданылуы былай тұрсын, тіпті медицинада, лингвистикада, ауыл шаруашылығы ғылымында қолдану мүмкіндігі өсіп келеді. Жалпы алғашында ықтималдықтар теориясы әдісін пайдаланған ғылым саласы жоқ деп айтуға болады. Соңғы жылдары ықтималдықтар теориясы әдісі әр түрлі ғылым және техника саласында қолданылып, оны жаңа жолға салды.
Тарихи мәлімдеме.
Ықтималдықтар теориясының негізгі ұғымдарын XVI-XVII ғ. Кардано, Гюйгенс, Паскаль, Ферма, тағы басқа оқымыстылар салды. Онан кейін ықтимал теориясын дамытуда Якова-Бернулли (1654-1705) көп еңбек етті. Оның «Үлкен сандар заңдылығы» деген теоремасы осы уақытқа дейінгі жиналған фактілердің теориялық дәлелдеме негіздері болды. Ықтималдықтар теориясына Пуассон және тағы басқа оқымыстылар еңбек сіңірді. Орыстың ұлы ғалымы П. Л. Чебышев (1821-1894) және оның оқушылары А. А. Марков (1856-1922) пен А. М. Ляпунов (1857-1918) ықтималдықтар теориясын дамытуға көп еңбек сіңірді. Олардан кейін, Совет математигі С. Н. Вернштейн, В. И. Романовский, А. Н. Колмогоров, А. Я. Хинчин, Б. Г. Гнеденко, Н. В. Смирнов ықтималдықтар теориясын тұрақты математикалық ғылым саласына көтерді.
Өзін өзі бақылау сұрақтары:
- Ең анық, мүмкін емес, кездейсоқ оқиғалардың анқтамаларын ата.
- Ықтимал пәнінің түсінігі.
- Кездейсоқ оқиғалардың мүмкіндіктері жайлы не білесіз?
- Ықтималдық теориясы қайда қолданылады?
- Ықтималдық теориясының тарихы.
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
2 - дәріс. Комбинаторика элементтері.
Сабақтың мақсаты: комбинаторика деген не екенін түсіндіру
Сабақтың жоспары:
- Қосылыстардың анықтамасы
- Орналастыру, алмастыру, теру
- Стирлиг формуласы
- Қайталанбалы қосылыстар: қайталнабалы орналастыру, алмастыру, теру
1. Қосылыстар анықтамасы.
Анықтама: Бірнеше нәрседен құралған топтардың бір-бірінен айырмашылығы не нәрселердің алынуы ретінде, не сол нәрселердің өзінде болып келсе, онда мұндай топтарды жалпы алғанда қосылыстар деп атайды.
2. Орналастыру, алмастыру, теру.
Анықтама:
 элементтің әрқайсысы
элементтің әрқайсысы
 -нен жасалған орналастыру деп әрқайсысында сол
-нен жасалған орналастыру деп әрқайсысында сол
 элементтің
элементтің
 -сі болып келетін және бір-бірінен өзгешелігі не элементінде, не элементтерінің ретінде болатын қосылыстарды айтады.
-сі болып келетін және бір-бірінен өзгешелігі не элементінде, не элементтерінің ретінде болатын қосылыстарды айтады.
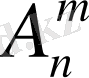 - n элементтен m жасалған орналастыру:
- n элементтен m жасалған орналастыру:
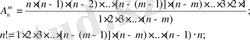 Equation. 3
Equation. 3
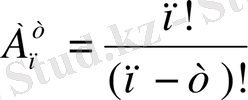
Анықтама:
 элементтен жасалған орналастырудың әрқайсысында
элементтен жасалған орналастырудың әрқайсысында
 элементтен болып келсе, бір-бірінен өзгешелігі тек элементтерінде болса, ондай орналастыруды
алмастыру
деп атаймыз. Ол мына формуламен өрнектеледі:
элементтен болып келсе, бір-бірінен өзгешелігі тек элементтерінде болса, ондай орналастыруды
алмастыру
деп атаймыз. Ол мына формуламен өрнектеледі:
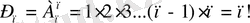 (1. 2)
(1. 2)
Анықтама:
 элементтің
элементтің
 -нен жасалған орналастырудың ішінен бір-бірінен өзгешелігі ең болмағанда бір элементінде болатынды таңдап алсақ, одан шығатын қосылысты
теру
деп атайды. Сөйтіп
-нен жасалған орналастырудың ішінен бір-бірінен өзгешелігі ең болмағанда бір элементінде болатынды таңдап алсақ, одан шығатын қосылысты
теру
деп атайды. Сөйтіп
 элементтің әрқайсысы
элементтің әрқайсысы
 -нен жасалған орналастырулардың барлық саны
-нен жасалған орналастырулардың барлық саны
 элементтің,
элементтің,
 -нен жасалған терулердің барлық саны
-нен жасалған терулердің барлық саны
 элементтен жасалған алмастырудың барлық санын көбейткенге тең болады.
элементтен жасалған алмастырудың барлық санын көбейткенге тең болады.
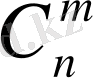 - теру белгісі.
- теру белгісі.
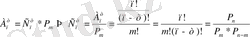 (1. 3)
(1. 3)
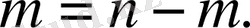
3. Стирлинг формуласы.
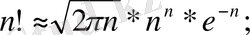
4. Қайталанбалы қосылыстар:
Анықтама:
Берілген әр түрлі
 -элементтен
-элементтен
 бойынша қайталанбалы орналастыру деп белгілі бір ретпен жазылған
бойынша қайталанбалы орналастыру деп белгілі бір ретпен жазылған
 элементтен тұратын қосылыстарды айтады. Мұнда әрбір элемент комбинацияға бірнеше рет кіруі мүмкін, қайталанбалы орналастырудың жалпы саны мына формуламен анықталады:
элементтен тұратын қосылыстарды айтады. Мұнда әрбір элемент комбинацияға бірнеше рет кіруі мүмкін, қайталанбалы орналастырудың жалпы саны мына формуламен анықталады:

Анықтама:
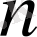 элементтен
элементтен
 элемент бойынша қайталанатын алмастыру деп
элемент бойынша қайталанатын алмастыру деп
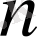 элементтен тұратын комбинацияларды айтады. Мұнда екі жағдай болуы мүмкін:
элементтен тұратын комбинацияларды айтады. Мұнда екі жағдай болуы мүмкін:
1)
 . Яғни, барлық элементтері әр түрлі болса, онда мына формуламен жазылады:
. Яғни, барлық элементтері әр түрлі болса, онда мына формуламен жазылады:
 ;
;
2)
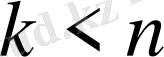 ,
,
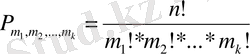 .
.
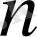 элемент бойынша қайталанбалы терулер деп бір-бірінен құрамы бойынша ажыратылатын комбинацияны айтады.
элемент бойынша қайталанбалы терулер деп бір-бірінен құрамы бойынша ажыратылатын комбинацияны айтады.
Өзін өзі бақылау сұрақтары:
- Қосылыстардың анықтамасы
- Онрналасу, алмасу және терудің анықтамалары мен формулаларын айтыңыз.
- Стирлинг формуласын жазыңыз.
- Қайталанбалы қосылыс деген не?
- Қайталанбалы қосылыстың анықтамасы.
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
3-дәріс. Ықтималдықтың классикалық, геометриялық, статистикалық анықтамалары.
Сабақтың мақсаты: Негізгі ұғымдарын түсіндіру
Сабақтың жоспары:
- Класскалық анықтама деген не?
- Геометриялық ықтималдық деген не?
- Салыстырмалы жиілік - статистикалық анықтама деген не?
- Олардың бір - бірінен өзгешелігі
1. Классикалық анықтамасы.
Анықтама: А оқиғасының қолайлы жағдай туғызатын m санының олардың тең мүмкіндікті үйлесімсіз элементарлық оқиғалары өзара толық топ жасайтын барлық нәтиже n санына қатынасын А оқиғасының ықтималы деп айтады. Сондықтан А оқиғасының ықтималдығы мына формуламен анықталады:
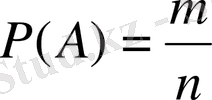
2. Геометриялық ықтималдық деген не.
 кесіндісі үлкен
кесіндісі үлкен
 кесіндісінің бөлігі болсын. Үлкен
кесіндісінің бөлігі болсын. Үлкен
 кесіндісіне ыңғайланып нүкте қойылған. Ол нүктенің кіші
кесіндісіне ыңғайланып нүкте қойылған. Ол нүктенің кіші
 кесіндісіне түсу ықтималдығы
кесіндісіне түсу ықтималдығы
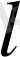 кесіндісінің ұзындығына пропорционал болады да, үлкен
кесіндісінің ұзындығына пропорционал болады да, үлкен
 кесіндісінің орналасуына байланысты болмайды. Сондықтан нүктенің
кесіндісінің орналасуына байланысты болмайды. Сондықтан нүктенің
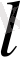 кесіндісіне түсу ықтималдығы мына формуламен анықталады:
кесіндісіне түсу ықтималдығы мына формуламен анықталады:
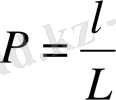 .
.
Сол секілді
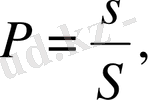
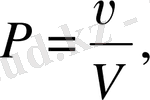
3. Салыстырмалы жилік- статистикалық анықтама деген не.
1-анықтама.
Салыстырмалы жиілік деп
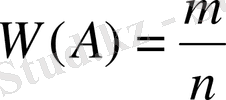 (1. 6) жасалған тәжірибеде А оқиғасының пайда болатын
(1. 6) жасалған тәжірибеде А оқиғасының пайда болатын
 санының жүргізілген тәжірибенің
санының жүргізілген тәжірибенің
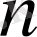 барлық санына қатынасын айтады.
барлық санына қатынасын айтады.
2-анықтама. Салыстырмалы жиілік кейде статистикалық ықтималдық деп те аталады.
4. Олардың бір - бірінен өзгешелігі.
Ықтималдықтың классикалық және статистикалық анықтамаларын салыстыра отырып, мынадай қорытындыға келуге болады: ықтималдықтың классикалық анықтамасы тәжірибеден міндетті түрде ең анық орындалуын қажет етпейді. Ал салыстырмалы жиіліктің анықтамасы міндетті түрде ең анық орындалатынын көрсетеді. Басқа сөзбен айтқанда, ықтималдықты классикалық тәжірибеге түскенге дейін, ал салыстырмалы жиілікті тәжірибеден соң есептеп шығарады. Шарттары бірдей тәжірибе жасаудан олардың әрбір байқауға түскен саны неғұрлым көп болса, онда ұзақ байқаудың нәтижесінде салыстырмалы жиіліктің белгілі бір тұрақтылық қасиеті болатыны байқалады. Ол қасиет, егер тәжірибеге түскен байқаудың саны көп болғанда, салыстырмалы жілік көп өзгеріске ұшырайды да, белгілі бір тұрақты санның арасында болады. Ол тұрақты санды оқиғаның пайда болу ықтималдығы деп атайды. Егер тәжірибе арқылы салыстырмалы жиілік анықталса, онда ол ықтималдықтың жуық шамасын көрсетеді:
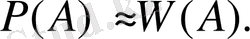
Өзін өзі бақылау сұрақтары:
- формуласымен не анықталады?
- Геометриялық ықтималдық тың формуласын жазыңыз.
- формуласын түсіндір.
- Салыстырмалы жиілік деген не?
- Ықтималдықтың классикалық анықтамасы мен салыстырмалы жиіліктің айырмашылығы қандай?
- Келесі формула нені көрсетеді?
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
4 - дәріс. Ықтималдықтың аксиомалық анықтамасы.
Сабақтың мақсаты: Акисомалық анықтамамен таныстыру.
Сабақтың жоспары:
- Жиын турлы түсінік: Екі оқиғаның қосындысы, көбейтіндісі, айырмасы туралы анықтамалар. Оқиғалардың белгілеулері.
- Кірістіру қатынастарының қасиеттері
- Ықтималдықтың аксиомалары
- Аксиома салдары
1. Жиын турулы түсінік: Екі оқиғаның қосындысы, көбейтіндісі, айырмасы турулы анықтамалар. Оқиғалардың белгілеулері.
1-анықтама. Қандай да бір белгілері бойынша біріктірілген заттар жиынтығын жиын деп айтамыз.
2-анықтама.
Екі оқиғаның А және В қосындысы дегеніміз -
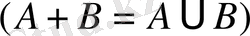 А және В оқиғаларының бірігуі.
А және В оқиғаларының бірігуі.
 - логикалық қосынды деп аталады.
- логикалық қосынды деп аталады.
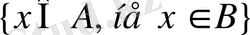
3-анықтама. А және В жиындарының көбейтіндісі деп элементтері А және В оқиғаларына ортақ элементтерден тұратын оқиғаны айтады.
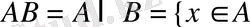 және
және

4-анықтама.
А және В оқиғаларының айырмасы деп
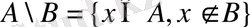 А оқиғасының элементтерінен тұрады да, В оқиғасының элементтері кірмейді.
А оқиғасының элементтерінен тұрады да, В оқиғасының элементтері кірмейді.
 - А оқиғасы
- А оқиғасы
 кеңістігінің бөлігі. Бұны кездейсоқ оқиға деп атаймыз. Кездейсоқ оқиғаны
кеңістігінің бөлігі. Бұны кездейсоқ оқиға деп атаймыз. Кездейсоқ оқиғаны
 т. б. деп белгілейміз.
т. б. деп белгілейміз.
2. Кірістіру қатынасының қасиеттері.
- - симметриялы қатынас; - симметриялы қарама-қарсы қатынас; - транзитивтік қатынас;
3. Ықтималдықтың аксиомалары.
Ω - ∀ қарапайым оқиғалардың жиынтығы. F - белгілі кездейсоқ оқиғалардың жүйесі. F - оқиғалар жүйесі оқиғалардың алгебрасы бола алады, егер мынадай шарт орындалса:
1)
 ;
;
2)
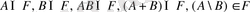 .
.
1-2 шарттардан
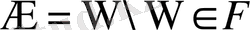 - жүйенің ең кіші бөлігі алгебраны жасайды,
- жүйенің ең кіші бөлігі алгебраны жасайды,
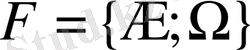 .
.
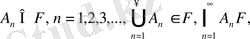 онда F алгебрасы оқиғаның сигма алгебрасы деп аталады.
онда F алгебрасы оқиғаның сигма алгебрасы деп аталады.
Анықтама. F жүйесінде анықталған Р(А) сандар функциясы А оқиғасының ықтималдығы деп аталады, егер төмендегідей аксиомаларды қанағаттандыратын болса:
- , онда;
- F жүйесі оқиғаладың алгебрасы;
- (ең анық оқиға) ;
- Егер А және В оқиғалары үйлесімсіз оқиғалар болса, онда, аддетивтік заң орындалады;
- ∀ кемімелі оқиғалардың(1) тізбектері F-тан шықса, онда(2) болады да, мынадай теңдікті қанағаттандырады:
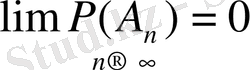 , F жүйесі
, F жүйесі
 алгебрасы болса және Р жоғарыдағы аксиомаларды қанағаттандыратын болса, онда
алгебрасы болса және Р жоғарыдағы аксиомаларды қанағаттандыратын болса, онда
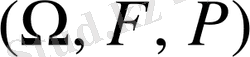 -
ықтималдықтар кеңістігі
деп аталады.
-
ықтималдықтар кеңістігі
деп аталады.
4. Аксиома салдары.
1)
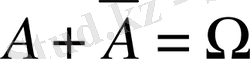 және 3, 4-ші аксиомаларды қолданып, мынаны аламыз:
және 3, 4-ші аксиомаларды қолданып, мынаны аламыз:
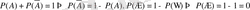 .
.
Егер
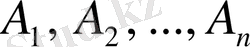 бір-бірімен қосарланып үйлесімсіз болса, яғни
бір-бірімен қосарланып үйлесімсіз болса, яғни
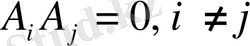 .
.
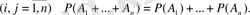
2) Егер
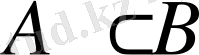 , онда
, онда
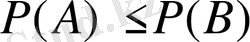 . Шынында
. Шынында
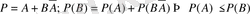
3)

Өзін өзі бақылау сұрақтары:
- Жиын дегеніміз не?
- Оқиғаларға қолданылатын амалдар және олардың анықтамалары.
- Кірістіру қатынаудың қасиеттерін атаңыз.
- Ықтималдық теориясының негізгі аксиомалары қандай?
- нені білдіреді?
- Аксиома салдарынайтыңыз.
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
5 - дәріс. Шартты ықтималдық.
Сабақтың мақсаты: Шартты ықтималдық деген не екенін түсіндіру.
Сабақтың жоспары:
- Шартты ықтималдық анықтамасы
- Тәуелсіз ықтималдық
- Ықтималдықтық көбейтіндісінің теоремасы
- Салдар
- Тәуелсіз екі оқиғаның көбейтіндісі. Салдар
- Жиынтығы тәуелсіз болатыноқиғаларының кем дегенде біреуінің пайда болу ықтималдығы
- Толық ықтималдықтың формуласы. Бейес формуласы
1. Шартты ықтималдық анықтамасы.
1-анықтама
. Екі оқиғаның (
 және
және
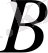 ) біреуінің шартты ықтималдығы деп бірінші оқиға
) біреуінің шартты ықтималдығы деп бірінші оқиға
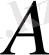 болып кеткеннен кейінгі пайда болатын ықтималдықты айтады. Оны былай белгілейді:
болып кеткеннен кейінгі пайда болатын ықтималдықты айтады. Оны былай белгілейді:
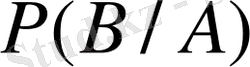 .
.
2. Тәуелсіз ықтималдық.
2-анықтама
. Егер
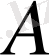 оқиғасы мен
оқиғасы мен
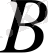 оқиғаларының біреуінің пайда болуы екіншісінің пайда болуына әсер етпейтін болса, онда мұндай оқиғаларды
тәуелсіз оқиғалар
дейді:
оқиғаларының біреуінің пайда болуы екіншісінің пайда болуына әсер етпейтін болса, онда мұндай оқиғаларды
тәуелсіз оқиғалар
дейді:
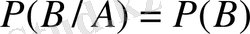 немесе
немесе
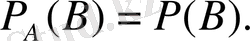 Тәуелсіз оқиғалардың шартты ықтималдығы шартсызға тең.
Тәуелсіз оқиғалардың шартты ықтималдығы шартсызға тең.
3. Ықтималдықтың көбейтіндісінің теоремасы.
теорема . Қатарынан пайда болған екі оқиғалардың көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығы мен екіншісінің шартты ықтималдығынң көбейтіндісіне тең болады. 1-ші формуладан:
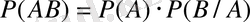
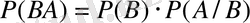
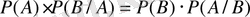
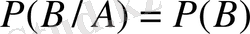
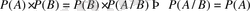
4 . Салдар.
Қатарынан пайда болған бірнеше оқиғалардың көбейтіндісінің ықтималдығы одан бұрынғы оқиғалар орындалғаннан кейін қалған барлық шартты ықтималдықтың көбейтіндісіне тең:
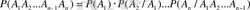 .
.
5. Тәуелсіз екі оқиғаның көбейтіндісі. Салдар.
теорема.
Тәуелсіз
 және
және
 оқиғалары үшін мынадай теорема лайықты:
оқиғалары үшін мынадай теорема лайықты:
 . Қатар пайда болған екі тәуелсіз оқиғалардың ықтималдығы олардың ықтималдығының көбейтіндісіне тең.
. Қатар пайда болған екі тәуелсіз оқиғалардың ықтималдығы олардың ықтималдығының көбейтіндісіне тең.
Салдар . Жиынтығы тәуелсіз болатын бірнеше оқиғалардың пайда болу ықтималдығы осы оқиғаларың ықтималдықтарының көбейтіндісіне тең:
 .
.
6.
Жиынтығы тәуелсіз болатын
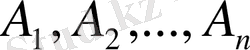 оқиғаларының кем дегенде біреуінің пайда болу ықтималдығы.
оқиғаларының кем дегенде біреуінің пайда болу ықтималдығы.
теорема
. Жиынтығы тәуелсіз болатын
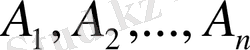 оқиғаларының кем дегенде біреуінің пайда болу ықтималдығы бір санымен
оқиғаларының кем дегенде біреуінің пайда болу ықтималдығы бір санымен
 қарама-қарсы оқиғалардың ықтималдықтарының көбейтіндісінің айырмасына тең:
қарама-қарсы оқиғалардың ықтималдықтарының көбейтіндісінің айырмасына тең:
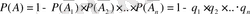 .
.
Егер
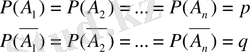 болса, онда
болса, онда
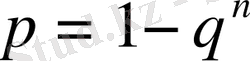 .
.
7. Толық ықтималдық формуласы. Бейес формуласы.
Теорема
. Толық топ құратын өзара үйлесімсіз оқиғалардың біреуі пайда болғанда ғана шартты түрде пайда болатын -
 оқиғасының ықтималдығы. Осы ықтималдық әрбіреуінің ықтималдығын
оқиғасының ықтималдығы. Осы ықтималдық әрбіреуінің ықтималдығын
 -ның оларға сәйкес шартты ықтималдықтарына көбейтіп, қосқанға тең:
-ның оларға сәйкес шартты ықтималдықтарына көбейтіп, қосқанға тең:
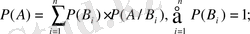
Бейес формуласы
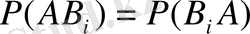
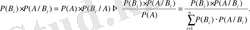
Өзін өзі бақылау сұрақтары:
- формуласымен нені анықтаймыз?
- Тәуелсіз ықтималдық формуласын жаз.
- Ықтималдықтың көбейтіндісінің теоремасын айтыңыз.
- формуласымен нені белгілейді.
- Тәуелсіз екі оқиғаның көбейтіндісін жаз.
- Мына формуламеннені белгілейміз?
- Бейс формуласын жаз.
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
6 - дәріс. Бернулли, Муавр-Лапластың формулалары.
Сабақтың мақсаты: Негізгі формулалармен таныстыру
Сабақтың жоспары:
- Күрделі оқиға деген не?
- Бір күрделі А оқиғасының n тәуелсіз тәжірибеде m рет пайда болуының, n-m рет пайда болмауының ықтималдығы тәуелсіз оқиғалардың көбейту теоремасы бойынша есептелінуі.
- Ізделінді ықтималдықүйлесімсіз оқиғалардың тәуелсіз оқиғаларды көбейту теоремасы бойынша есептелінуі
- Оқиғаның n тәуелсіз тәжірібеде: а) m реттен аз; б) m реттен көп; в) m реттен кем емес г) m реттен көп емес
- Муавр - Лапластың локальдық теоремасы
- Муавр - Лапластың интегралдық теоремасы
1. Күрделі оқиғалар деген не.
Анықтама . Бірнеше жиынтықтан құралған жиынтықты күрделі оқиға дер атаймыз.
2.
Бір рет күрделі
 оқиғасының
оқиғасының
 тәуелсіз тәжірибеден
тәуелсіз тәжірибеден
 рет пайда болуының
рет пайда болуының
 ықтималдығы тәуелсіз оқиғаларды көбейту теоремасы бойынша есептелінуі:
ықтималдығы тәуелсіз оқиғаларды көбейту теоремасы бойынша есептелінуі:

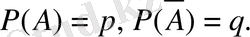
3 . Ізделінді ықтималдық.
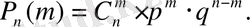
Үйлесімсіз оқиғалардың ықтималдықтары қосу ережесі бойынша есептелінеді:
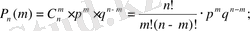
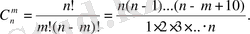
4.
Оқиғаның
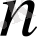 тәуелсіз тәжірибеде:
тәуелсіз тәжірибеде:
а)
 реттен аз:
реттен аз:
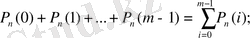
б)
 реттен көп:
реттен көп:
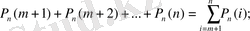
в)
 реттен кем емес:
реттен кем емес:
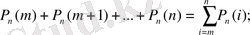
г)
 реттен көп емес:
реттен көп емес:
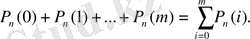
5. Муавр-Лапластың локальдық теоремасы
Теорема
. Оқиғаның әрбір тәжірибеде (сынақта) пайда болу ықтималдығы
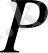 тұрақты
тұрақты
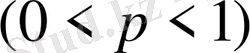 болса, онда оқиғаның
болса, онда оқиғаның
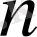 тәуелсіз тәжірибеде (сынақта)
тәуелсіз тәжірибеде (сынақта)
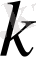 рет пайда болу ықтималдығы мынадай жуық мәнге тең:
рет пайда болу ықтималдығы мынадай жуық мәнге тең:
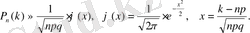
Функцияның мәндерінің
 үшін кестесі берілген, ал
үшін кестесі берілген, ал
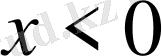 болғанда да осы кестені пайдалануға болады. Себебі
болғанда да осы кестені пайдалануға болады. Себебі
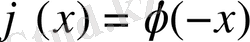 - жұп функция.
- жұп функция.
6. Муавр-Лапластың интегралдық теоремасы
Теорема.
 оқиғаларының әр тәжірибеде пайда болу ықтималдығы
оқиғаларының әр тәжірибеде пайда болу ықтималдығы
 тұрақты
тұрақты
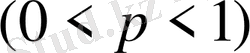 болса, онда
болса, онда
 оқиғасының
оқиғасының
 тәуелсіз тәжірибелерде
тәуелсіз тәжірибелерде
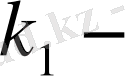 ден кем емес,
ден кем емес,
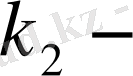 ден артық емес пайда болу ықтималдығы мына формула бойынша жуықтап есептелінеді:
ден артық емес пайда болу ықтималдығы мына формула бойынша жуықтап есептелінеді:
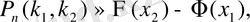 мұндағы
мұндағы
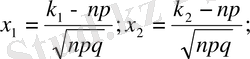
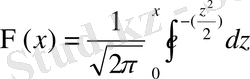 - Лаплас функциясы деп аталады.
- Лаплас функциясы деп аталады.
Лаплас функциясының кестесі Гнеденконың кітабында келтірілген
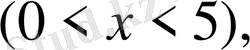 ал
ал
 болса біз функцияны
болса біз функцияны
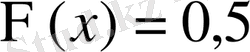 деп санаймыз.
деп санаймыз.
Өзін өзі бақылау сұрақтары:
- Күрделі оқиғалар деген не?
- формуласымен нені анықтайды?
- Ізделінді ықтималдық дегенді қалай түсінесіз?
- Муавр-Лапластың интегралдық теоремасы қандай?
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
7- дәріс. Кездейсоқ шамалар.
Сабақтың мақсаты: кездейсоқ шамалардың негізгі ұғымдарын түсіндіру.
Сабақтың жоспары:
- Кездейсоқ шамалардың анықтамалары
- Кездейсоқ шамалардың дискретті және үздіксіз болып бөлінуі
- Fжүйесіалгебрасы болғандағы негізгі формулалар
- Үлестіру функциясының анықтамасы
- Үлестіру функциясының қасиеттері
- Үздіксіз кедейсоқ шамалар
- Кездейсоқ шаманың абсолюттік түрі
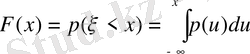
Мұндағы P(x) - үлестіру тығыздығы
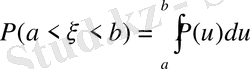
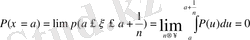
- x P(x) функциясының үздіксіз нүктесі болса, онда
- Үлестіру тығыздығының қасиеттері
1 . Кездейсоқ шамалардың анықтамалары .
Анықтама. Кездейсоқ шама деп сандық мән қабылдайтын, бірақ қандай мән қабылдайтынын алдын ала болжап айту мүмкін болмайтын шамаларды айтады.
Кездейсоқ шамаларды латын алфавитінің бас әріптерімен
 немесе гректің кіші әріптерімен
немесе гректің кіші әріптерімен
 белгілейді. Ал олардың қабылдайтын мәндерін латынның кіші әріптерімен
белгілейді. Ал олардың қабылдайтын мәндерін латынның кіші әріптерімен
 белгілейді.
белгілейді.
2 . Кездейсоқ шамалардың дискретті және үздіксіз болып бөлінуі.
Кездейсоқ шамаларды қабылдайтын мәндеріне қарай дискретті және үздікті болып бөлінеді.
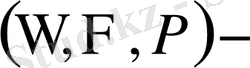 ықтималдық кеңістік болып табылады. Осы айтылғандардан келесі қорытынды анықтама шығады.
ықтималдық кеңістік болып табылады. Осы айтылғандардан келесі қорытынды анықтама шығады.
Анықтама.
Кез келген нақты сандар мәніндегі
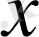 үшін
үшін
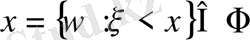 берілген нақты функция
берілген нақты функция
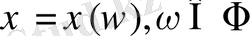 кездейсоқ шама
деп аталады.
кездейсоқ шама
деп аталады.
3.
 жүйесі
жүйесі
 алгебрасы болғандағы негізгі формулалар.
алгебрасы болғандағы негізгі формулалар.
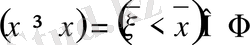
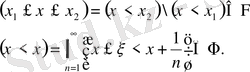
4. үлестіру функциясының анықтамасы.
Анықтама
.
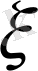 кездейсоқ шамасының мәндері тиянақты
кездейсоқ шамасының мәндері тиянақты
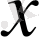 санынан кіші болу ықтималдығын
санынан кіші болу ықтималдығын
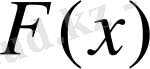 үлестіру функциясы
дейміз.
үлестіру функциясы
дейміз.
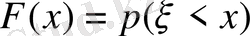
Анықтама бойынша бұл функция - интегралды.
Егер
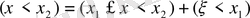 болса, онда 4-аксиома бойынша
болса, онда 4-аксиома бойынша
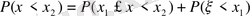 болады.
болады.
(1. 11)
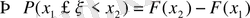 (1. 12)
(1. 12)
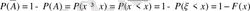
(1. 11) +(1. 12)
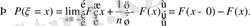
5. Үлестіру функциясының қасиеттері.
- Егерболса, ондажәнекемімейтін функция болады;
Осы қасиеттерді жалпы түрде келесі теңсіздікпен жазуға болады. :
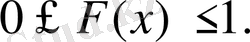
6. Үздіксіз кездейсоқ шама.
Анықтама . Егер кездейсоқ шама қайсібір шекті және шексіз аралықтардың барлық мәндерін қабылдайтын болса, онда мұндай шамалар үздіксіз шамалар деп аталады.
Үздіксіз кездейсоқ шамалардың қабылдайтын мәндері шексіз. Үлестіру функциясы ұғымы ықтималдық теориясында ең негізгі ұғым болып табылады. Сондықтан үздіксіз кездейсоқ шамаға осы ұғымды қолдана отырып келесі анықтаманы беруге болады.
Анықтама
. Егер кездейсоқ шаманың үлестіру функциясы
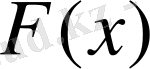 үздіксіз болса, онда кездейсоқ шама
үздіксіз
деп аталады.
үздіксіз болса, онда кездейсоқ шама
үздіксіз
деп аталады.
7. Кездейсоқ шаманың абсолюттік түрі.
Кездейсоқ шаманың абсолюттік түрі деп кез келген теріс емес болғандағы үлестіру функциясын айтады:
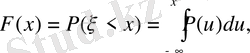 (1. 13)
(1. 13)
мұндағы
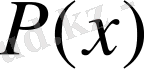 функциясы
үлестіру тығыздығы
деп аталады, ал кейде оны ықтималдықтың дифференциалдық функциясы деп атайды. Онда сәйкес
функциясы
үлестіру тығыздығы
деп аталады, ал кейде оны ықтималдықтың дифференциалдық функциясы деп атайды. Онда сәйкес
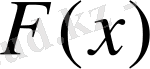 функциясын ықтималдықтың үлестіруінің интегралдық функциясы жап атайды:
функциясын ықтималдықтың үлестіруінің интегралдық функциясы жап атайды:
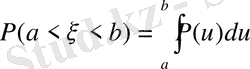
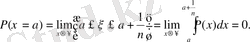
8. Егер
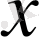
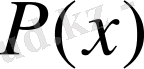 функциясының үздіксіз нүктесі болса, онда
функциясының үздіксіз нүктесі болса, онда
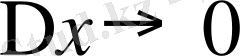 болған кезде
болған кезде
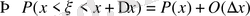 болады.
болады.
9. Үлестіру тығыздығы төмендегі қасиеттермен сипатталды:
Өзін өзі бақылау сұрақтары:
- Кездейсоқ шамалардың анықтамаларын айтыңыз.
- Кездейсоқ шамалар қалай бөлінеді?
- алгебрасындағы негізгі формулаларды көрсет.
- Үлестіру функциясы деген не?
- Үлестіру функциясының қасиеттері қандай?
- Үздіксіз кездейсоқ шама дегеніміз не?
- Кездейсоқ шаманың түрлері қандай?
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
8 - дәріс. Дискретті және үздіксіз шамалардың математикалық үміттері.
Сабақтың мақсаты: математикалық ұғымы қалай пайда болғанын түсіндіру
Сабақтың жоспары:
- Дискретті кездейсоқ шаманың математикалық үміті
- Дискретті кездейсоқ шаманың математикалық үмітініңқасиеттері
- Үздіксіз кездейсоқ шаманың математикалық үміті, оның қасиеттері
1. Дискретті кездейсоқ шаманың математикалық үміті.
Кездейсоқ шаманың ықтималдық үлестіру заңын біле отырып, оның кейбір сандық сипаттамаларын есептеуге болады. Сол сипаттамалардың бірі математикалық үміт болып табылады.
Анықтама. Дискретті кездейсоқ шамалардың мүмкін болатын мәндерінің сәйкес ықтималдықтарына көбейтінділерінің қосындысын математикалық үміт деп атаймыз.
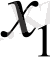
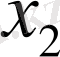
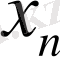

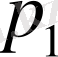

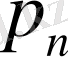
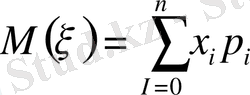 ,
,
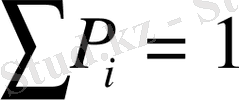 , болғандықтан
, болғандықтан
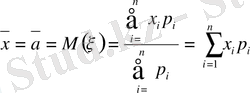
Сондықтан математикалық үміт кездейсоқ шаманың орта мәні деп аталады.
Анықтама.
 - берілген дискретті кеңістіктегі
- берілген дискретті кеңістіктегі
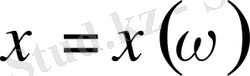 кездейсоқ шаманың математикалық үміті деп
кездейсоқ шаманың математикалық үміті деп
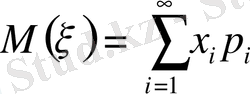 санын және осы қатардың абсолюттік жинақты болуын айтады, яғни
санын және осы қатардың абсолюттік жинақты болуын айтады, яғни
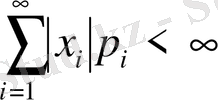 .
.
- Дискретті кездейсоқ шаманың математикалық үмітінің қасиеттері.
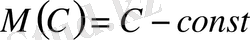 - математикалық үміттің тұрақтысы сол тұрақтыға тең.
- математикалық үміттің тұрақтысы сол тұрақтыға тең.
- Үздіксіз кездейсоқ шаманың математикалық үміті және қасиеті.
Анықтама.
Берілген
 - үздіксіз кеңістіктегі
- үздіксіз кеңістіктегі
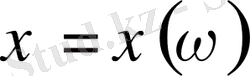 кездейсоқ шаманың математикалық үміті
кездейсоқ шаманың математикалық үміті
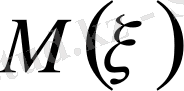 деп
деп
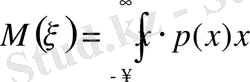 - санын және осы интегралдың
- санын және осы интегралдың
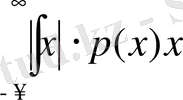 абсолютті жинақты болуын айтады.
абсолютті жинақты болуын айтады.
Анықтама.
Егер кездейсоқ үздіксіз шаманың мүмкін болатын мәндері
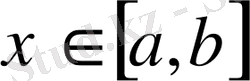 болса, онда бұл аралықтың сыртында үлестіру тығыздығы
болса, онда бұл аралықтың сыртында үлестіру тығыздығы
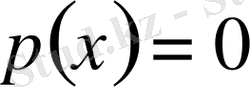 болады, ендеше:
болады, ендеше:
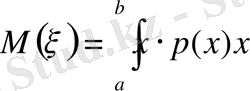 .
.
Математикалық үміттің қасиеттері:
- Алдынғы үш түрлі қасиеті дәл дискретті кездейсоқ шаманың қасиеттері сияқты;
- .
Өзін өзі бақылау сұрақтары:
- Математикалық үміт дегенді қалай түсінесіз?
- Дискретті кездейсоқ шаманың математикалық үміті деген не?
- Математикалық үміттің қасиеттерін көрсет.
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
9 - дәріс . Дисперсия және орта квадраттық ауытқуы.
Сабақтың мақсаты: Дисперсия деген ұғым қалай пайда болағын айту.
Сабақтың жоспары:
- Дисперсияның анықтамасы
- Ортаквадраттық ауытқу
- Дисперсияның қасиеттері
- Үздіксіз және дискретті кездейсоқ шамалардың дисперсиялары
1. Дисперсияның анықтамасы.
Анықтама.
 -
кездейсоқ шаманың дисперсиясы деп
-
кездейсоқ шаманың дисперсиясы деп
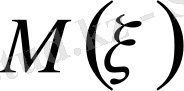 математикалық үміті бар санды айтады.
математикалық үміті бар санды айтады.
2. Орта квадраттық ауытқуы.
Анықтама.
 -
кездейсоқ шаманың орташа квадраттық ауытқуы деп
-
кездейсоқ шаманың орташа квадраттық ауытқуы деп
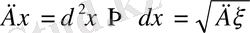 оң жағындағы түбір астындағы дисперсиядан шыққан санды айтады.
оң жағындағы түбір астындағы дисперсиядан шыққан санды айтады.
- Дисперсияның қасиеттері.
-
 кез келген шама үшін
кез келген шама үшін
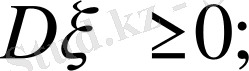
- егер c=const болса, онда
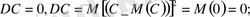
- егер c=const болса, онда

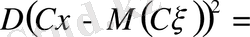
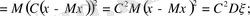
4. Үздіксіз және дискретті кездейсоқ шамалардың дисперсиялары .
 -
кездейсоқ шама үздіксіз болса, онда:
-
кездейсоқ шама үздіксіз болса, онда:
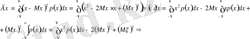
сонда
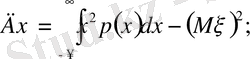
 -
кездейсоқ шама дискретті болса, онда:
-
кездейсоқ шама дискретті болса, онда:
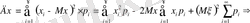
Сонда
Өзін өзі бақылау сұрақтары:
- Дисперсияның анықтамасын айтыңыз.
- Орта квадраттық ауытқу деген не?
- Дисперсияның қасиеттерін ата.
Силлабус соңындағы негізгі әдебиеттер тізімінен 1, 5-7 әдебиеттерді қарастыруға болады.
10 - дәріс. Теориялық моменттер. Кездейсоқ шаманың модасы мен медианасы. Ассиметрия, эксцесі.
Сабақтың мақсаты: Негізгі ұғымдармен таныстыру
Сабақтың жоспары:
- Дискертті және үздіксіз кездейсоқ шамалардың бастапқы моменттері
- Дискретті және үздіксіз кездейсоқ шамалардың орталық монеттері
- Ассиметрия және эксцес деген не?
- Кездейсоқ шамалардың модасы және медианасы
1 . Дискретті және үздіксіз кездейсоқ шамалардың бастапқы моменттері.
1-Анықтама.
Үлестірім заңы арқылы берілген
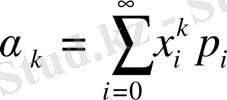 қатар
қатар
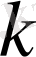 -ретті дискретті кездейсоқ шаманың
бастапқы моменті
деп аталады.
-ретті дискретті кездейсоқ шаманың
бастапқы моменті
деп аталады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz