Ықтималдықтар теориясы (1 кредит): негіздер, аксиомалар, шартты ықтималдық, комбинациялық талдау және биномдық үлестірім


2. 2. Дәрістер тезистері
1-Кредит. ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫ
1-дәріс.
1-тарау. Ықтималдықтар теориясының негіздері.
§1. Кездейсоқ оқиғалар.
Жеке құбылыстар мен деректерді немесе олардың аз мөлшердегі көріністерін бақылау құбылыстардың пайда болу заңдылықтарын және өзара байланыстарын анықтауға мүмкіндік бере бермейді. Сондықтан ол құбылыстарға кездейсоқ жайттар ретінде қараймыз. Бірақ, біртекті құбылыстар мен деректер жаппай көрініс тапса, олардың табиғатына тән заңдылықтарды байқауға болады.
Ықтималдықтар теориясы және оған негізделген математикалық статистика біртекті жаппай кездейсоқ құбылыстардың үлестірілу заңдылықтарын зерттейтін математикалық ғылымдар. Математикалық абстракциялау- байқалып отырған құбылыстарды олардың нақты табиғатына байланыссыз зерделеу құбылыстардың мейлінше кең класына қолдануға жарамды ғылыми негізделген жалпы заңдылықтар мен қағидаларды айқындауға мүмкіндік береді. Ал, ол заңдарды іс жүзінде қолдану ықтималдықтар теориясының негізгі ережелерін сақтауды, зерттеліп отырған құбылыстар мен процесстерге қатысты материалдарды дұрыс статистикалық өңдеуді талап етеді.
Шарттар мен амалдардың белгілі бір жиынтығын орындауды сынақ немесе тәжірибе дейміз, оның қорытындысы сынақ нәтижесі болады. Кездейсоқ нәтиже беретін тәжірибе кездейсоқ эксперимент деп, ал нәтиженің өзі кездейсоқ (мүмкін) оқиға деп аталады. Сынақтың барлық мүмкін нәтижелерінің жиынтығы- кездейсоқ эксперименттің элементар бітістерінің жиыны (оқиғалар өрісі) Ω арқылы, ал қандайда болмасын нысанадағы (біз көздеген) кездейсоқ оқиғаның пайда болуын қамтамасыз ететін нәтижелердің жиыны ω арқылы белгіленеді.
Сынақ қорытындысында пайда бола алмайтын нәтиже: ω=0 ( құр жиын) мүмкін емес оқиға деп аталады. Ал, ω=Ω болып, пайда болуы міндетті, сынақтың бірден-бір мүмкін қорытындысы болатын нәтиже- ақиқат оқиға деп аталады. Қалған жағдайларда енбе жиындар қатынасына:ω
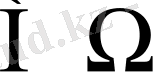 келеміз. Кездейсоқ оқиғаларға жиындар теориясы тұрғысынан қарау жиындарға қолданылатын амалдарды кездейсоқ оқиғаларға да қолдануға мүмкіндік береді. Сынақтың элементар нәтижелерін кеңістіктегі (жазықтықтағы, кесіндідегі) нүктелер арқылы белгілей отырып, бұл амалдарды геометриялық тұрғыдан талқылауға да жол ашады.
келеміз. Кездейсоқ оқиғаларға жиындар теориясы тұрғысынан қарау жиындарға қолданылатын амалдарды кездейсоқ оқиғаларға да қолдануға мүмкіндік береді. Сынақтың элементар нәтижелерін кеңістіктегі (жазықтықтағы, кесіндідегі) нүктелер арқылы белгілей отырып, бұл амалдарды геометриялық тұрғыдан талқылауға да жол ашады.
Оқиғаларды латын алфавитінің бас әріптерімен: A, B, C… белгілейді. Сынақ нәтижесінде бір мезгілде пайда бола алатын оқиғаларды, мысалы, A және B бірігетін оқиғалар дейміз. Оларға қолайлы нәтижелердің жиындары ω(A) және ω(B) қиылысушы жиындар (1-сурет) болады. Қарсы жағдайда
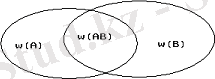
1-сурет
:
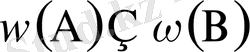 =0 A және B бірікпейтін оқиғалар болады. Ал,
=0 A және B бірікпейтін оқиғалар болады. Ал,
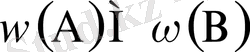 қатынасы B оқиғасы әруақытта A-ға ілесе пайда болатынын білдіреді. Қысқаша
қатынасы B оқиғасы әруақытта A-ға ілесе пайда болатынын білдіреді. Қысқаша
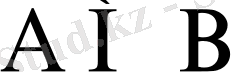 және
және
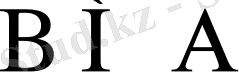 болса, эквивалент (балама) жиындар ұғымына келеміз: A=B, оқиғалар тепе-теңдігі орын алады.
болса, эквивалент (балама) жиындар ұғымына келеміз: A=B, оқиғалар тепе-теңдігі орын алады.
Оқиғалар қосындысы-жиындардың бірігуі :A+B=ω(A)
 ω(B) - қосылғыш оқиғалардың кем дегенде біреуі пайда болса жарайтынын сипаттайтын оқиға. Оқиғалардың көбейтіндісі- жиындардың қимасы (айқасуы) :
ω(B) - қосылғыш оқиғалардың кем дегенде біреуі пайда болса жарайтынын сипаттайтын оқиға. Оқиғалардың көбейтіндісі- жиындардың қимасы (айқасуы) :
AB=ω(A)
 ω(B) - көбейткіш оқиғалардың қосарлана пайда болуын білдіретін оқиға. Оқиғалардың айырымы
ω(B) - көбейткіш оқиғалардың қосарлана пайда болуын білдіретін оқиға. Оқиғалардың айырымы
A-B=ω(A) ×ω(B) жиын ретінде A-ға тиісті, бірақ, B-ның құрамына енбейтін элементтерден тұрады. Ал, оқиға ретінде ол A-ның пайда болып, B -ның жоқ екенін өрнектейді. Сынақтың бірден-бір мүмкін нәтижесі бола тұра, бірікпейтін A және Ā оқиғаларын қарама-қарсы оқиғалар дейміз. Бұл жағдайда ω(Ā) =Ω×ω(A) ω(A) жиынының Ω-ға дейінгі толықтауышы деп аталып, сынақтың
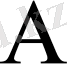 оқиғасының пайда болуын жоққа шығаратын элементар нәтижелерінен ғана тұрады.
оқиғасының пайда болуын жоққа шығаратын элементар нәтижелерінен ғана тұрады.
Оқиғаларға қолданылатын амалдар төмендегі заңдарға бағынады:
коммутативтік заң (орын алмастыру) :
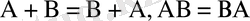
ассоциативтік (терімділік) заң (топтастыру) :
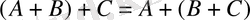 ,
,
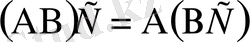
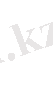
көбейтудің қосуға қарағандағы дистрибутивтігі (үлестірімділігі)
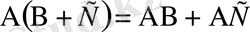 .
.
Кездейсоқ эксперименттің бірден-бір мүмкін элементар нәтижелері
2-сурет
 қос-қостан бірікпейтін болса,
қос-қостан бірікпейтін болса,
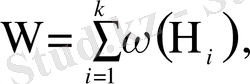
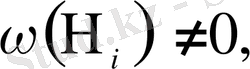
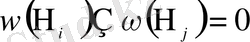 ,
,
( i, j =1,
 , k),
, k),
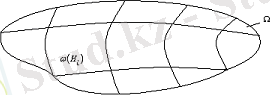
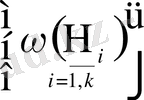 жиындар системасын Ω жиынының бөлшектенуі (2-сурет) деп атап,
жиындар системасын Ω жиынының бөлшектенуі (2-сурет) деп атап,
 оқиғалардың толық тобын (жүйесін) құрайды дейміз.
оқиғалардың толық тобын (жүйесін) құрайды дейміз.
§2. Оқиға ықтималдығының аксиомалық анықтамалары.
1. Статистикалық анықтама.
Кездейсоқ эксперимент шарттары өзгермеген күйінде N рет қайталанды, соның ішінде біз мүдделі болып отырған оқиға M (0
 ) рет байқалды делік;
) рет байқалды делік;
 және
және
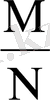 сандары оқиғаның пайда болуының (табыстың) абсолют және салыстырмалы жиіліктері деп аталады. Соңғы қатынас табыс жиілігінің негізгі көрсеткіші болып саналады. Қайталану сандары (көлемдері) N әр түрлі сынақтардың бірнеше сериясы (топтамасы) орындалсын. Топтамалардың көлемдері шағын болса, олардағы табыс жиіліктерінің бір-бірінен ауытқуы да елеулі болуы мүмкін. Топтамалардың көлемдері өскен сайын (N→∞) бұл ауытқулар азайып, табыс жиілігінің мәндері тұрақтанып, олардың тізбегі бір нақты p санының маңына шоғырлана, топтана түседі. Бұл сан тәжірибеде табыстың пайда болуының объективтік мүмкіндігінің өлшемін (дәрежесін) анықтайды.
сандары оқиғаның пайда болуының (табыстың) абсолют және салыстырмалы жиіліктері деп аталады. Соңғы қатынас табыс жиілігінің негізгі көрсеткіші болып саналады. Қайталану сандары (көлемдері) N әр түрлі сынақтардың бірнеше сериясы (топтамасы) орындалсын. Топтамалардың көлемдері шағын болса, олардағы табыс жиіліктерінің бір-бірінен ауытқуы да елеулі болуы мүмкін. Топтамалардың көлемдері өскен сайын (N→∞) бұл ауытқулар азайып, табыс жиілігінің мәндері тұрақтанып, олардың тізбегі бір нақты p санының маңына шоғырлана, топтана түседі. Бұл сан тәжірибеде табыстың пайда болуының объективтік мүмкіндігінің өлшемін (дәрежесін) анықтайды.
Көп мөлшерде қайталанған сынақтарда маңына оқиғаның пайда болу жиілігінің мәндері топтанатын P (
 ) саны сол оқиғаның ықтималдығы деп аталады.
) саны сол оқиғаның ықтималдығы деп аталады.
Ықтималдықтың статистикалық анықтамасы деп аталатын бұл сөйлемді қолдану алдын ала сынақтар өткізіп, олардың нәтижелерін статистикалық өңдеуді талап етеді. Бұл талаптың әсіресе теориялық зерттеулерде қиындығы мол.
2. Классикалық анықтама. Қайталанба сынақтарда оқиғалардың пайда болу жиіліктерінің тәртібін зерттеп, байқалған деректерді жалпылау және салыстырмалы жиіліктер қасиеттерін абстракциялау ықтималдық түсінігінің классикалық (аксиомалық) анықтамасына келтірді. Ықтималдықтың қазіргі аксиомалық теориясын 1933 ж. А. Н. Колмогоров жасады.
Сынақты өткізу шарттары нәтижелердің қай-қайсысына да басқаларына қарағанда артықшылық бермейтін болса, сынақ нәтижелері тең мүмкіндікті (теңықтималды) деп аталады. Мұндай сынақтардың классикалық мысалы ретінде урнадағы (қоржындағы) бір-бірінен сипап ажыратылмайтын шарлардың бірнешеуін тәуекел алып шығуды атауға болады. Бұл тектес тәжірибелерді математикалық тәріздеу (модельдеу) ықтималдықтар теориясында классикалық схема (тәсім) немесе урналар тәсілі деген атпен белгілі.
Кездейсоқ эксперименттің тең мүмкіндікті нәтижелері оқиғалардың толық тобын
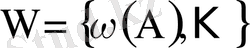 құрайды десек, ω(A) A оқиғасының пайда болуына қолайлы нәтижелердің жиыны болады; Ω және ω шекті жиындар, оларды құрайтын элементтердің сандары сәйкес N(Ω) =n, N(ω) =m десек, A оқиғасының ықтималдығы
құрайды десек, ω(A) A оқиғасының пайда болуына қолайлы нәтижелердің жиыны болады; Ω және ω шекті жиындар, оларды құрайтын элементтердің сандары сәйкес N(Ω) =n, N(ω) =m десек, A оқиғасының ықтималдығы
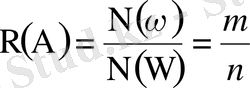 (1. 1)
(1. 1)
сандық функциясымен анықталады. Олай болса, кездейсоқ сынақта оқиғаның пайда болу ықтималдығы оған қолайлы нәтижелер санының барлық мүмкін нәтижелердің санына қатынасына тең.
Мүмкін емес оқиға үшін m=0, ақиқат оқиға үшін m=n, ал басқа кездейсоқ оқиғалар үшін
 <m<1, демек
<m<1, демек
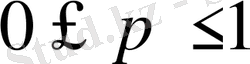 . «Классикалық ықтималдық формуласымен » (1. 1) анықталатын шама кәміл (шартсыз) ықтималдық деп аталып, ықтималдықтардың үш аксиомасына (шартына) қанағаттандырады:
. «Классикалық ықтималдық формуласымен » (1. 1) анықталатын шама кәміл (шартсыз) ықтималдық деп аталып, ықтималдықтардың үш аксиомасына (шартына) қанағаттандырады:
P(A) ≥0;
толық топ құрайтын оқиғалардың ықтималдықтарының қосындысы бірге тең:
 ,
,
 ;
;
қос-қостан бірікпейтін оқиғалардың кезкелген шекті не шексіз тізбегі
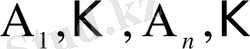
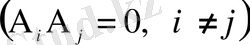 үшін
үшін
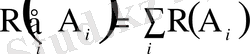 .
.
3. Геометриялық ықтималдық.
Үзіксіз Ω және ω жиындары сандық осьте
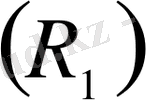 , жазықтықта
, жазықтықта
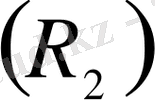 немесе кеңістікте
немесе кеңістікте
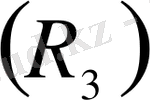 белгілі бір аймақ құрайды.
белгілі бір аймақ құрайды.
(3-сурет) .
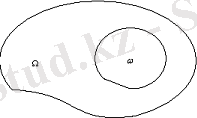
3-сурет
Сәйкес аралықтың ұзындығын, жазық фигураның ауданын немесе дененің көлемін сол нысандармен анықталатын жиынның өлшемі (mesure) деп атап, mes(Ω), mes(ω) немесе, қысқаша, m(Ω), m(ω) арқылы белгілейміз. Өлшемі шекті аймақты сәйкес кеңістікте
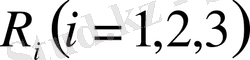 квадратталатын (кубталатын) аймақ дейміз.
квадратталатын (кубталатын) аймақ дейміз.
Квадратталатын аймақтар үшін
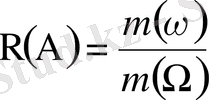 (1. 2)
(1. 2)
1-есеп.
Бекетке келген жолаушы пойызы 13 вагоннан тұрады. Оның 5-уі купелі (бөлмелі), 4-і плацкартты, 2-і ұйқы-жай, қалғандары бір-бірден жұмсақ және почта вагондары. Тепловозды ағытқаннан кейін перронға тәуекел шыққан қарсы алушының бөлмелі вагон тұсына тап келу (Α оқиғасы) ықтималдығын табыңыз.
Шешу. Мұнда n=13, m=5. Сондықтан P(A) =5/13 .
§3. Қосылыстар теориясы элементтері.
Берілген Ω жиынының элементтерінен құрылған оған кірме әр түрлі
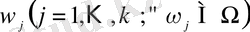 жиындары қосылыстар (комбинациялар) деп, математиканың қосылыстар теориясын зерттейтін бөлімі комбинациялық талдау деп аталады. Бұл бөлімнің негізгі принципі- көбейту ережесі : егер әрбір
жиындары қосылыстар (комбинациялар) деп, математиканың қосылыстар теориясын зерттейтін бөлімі комбинациялық талдау деп аталады. Бұл бөлімнің негізгі принципі- көбейту ережесі : егер әрбір
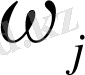 қосылысын
қосылысын
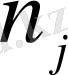 тәсілмен құру мүмкін болса, онда бірге алғанда олардың бәрі
тәсілмен құру мүмкін болса, онда бірге алғанда олардың бәрі
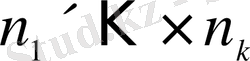 тәсілмен құрылады.
тәсілмен құрылады.
Әр элементіне сандардың натурал қатарынан номер тағылған шекті жиынды реттелген жиын дейміз. Реттелген шексіз жиын санамалы жиын делінеді.
Бір-бірінен элементтерінің ретімен (орындарымен) ғана ажыратылатын n элементті әр түрлі (реттелген) жиындар n элементтен жасалған орынауыстырулар деп аталады. Олардың саны
 ! (1. 3)
! (1. 3)
Реттелген болуы міндетті емес Ω және ω (ω
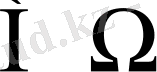 ) жиындары сәйкес n және m (m≤n) элементтен құрылған делік. Бір-бірінен құрамымен ғана (реті ескерілмей) ажыратылатын барлық ω қосылыстары n элементтен
) жиындары сәйкес n және m (m≤n) элементтен құрылған делік. Бір-бірінен құрамымен ғана (реті ескерілмей) ажыратылатын барлық ω қосылыстары n элементтен
m-нен жасалған терулер деп аталады. Олардың саны
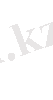
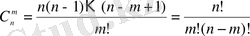 (1. 4)
(1. 4)
Ньютон биномның формуласын енді
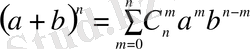 (1. 5)
(1. 5)
түрінде жазуға болатындықтан (1. 4) сандары биномдық коэффициенттер деп те аталады. Олардың «симметриялық қасиеті» бар және рекурренттік қатынастарды қанағаттандырады:
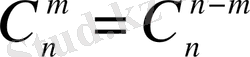 ,
,
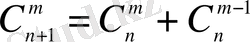 (1. 6)
(1. 6)
Жеке жағдайда: a=b=1 (1. 5) -тен
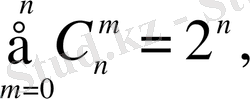
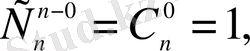

Бір-бірінен не құрамымен, не элементтерінің ретімен ажыратылаты n элементтен m-нен (m≤n) жасалған қосылыстар n элементтен m-нен жасалған орналастырулар деп аталады. Әрбір n элементтен m-нен жасалған теруден орын ауыстырулар арқылы m! орыналастырын жасауға болады. Ендеше, n элементтен m-нен жасалған орналастырулардың саны
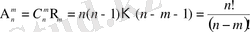 (1. 7)
(1. 7)
Шекті (n элементі бар, реттелген болуы міндетті емес) Ω жиыны кездейсоқ үлгіде сәйкес
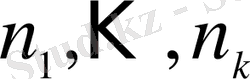 элементтен тұратын k кірме жиындарға
элементтен тұратын k кірме жиындарға
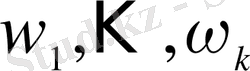
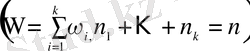 бөлшектенген десек, бөлшектеу әдістерінің саны
бөлшектенген десек, бөлшектеу әдістерінің саны
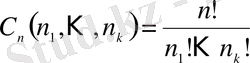 (1. 8)
(1. 8)
Бұл (полиномдық тәсіл) биномдық схеманың жалпыланған түрі. Шынында да, (1. 8) -де
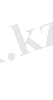 k=2 (
k=2 (
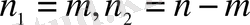 Equation. 3 ) десек, (1. 4) -ке келеміз.
Equation. 3 ) десек, (1. 4) -ке келеміз.
Енді Ω жиынына кірме құрамында
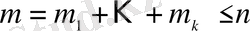 Equation. 3
Equation. 3
элементі бар реттелмеген қосылыс құралық. Әрбір
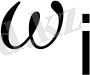 Equation. 3 -ден
Equation. 3 -ден
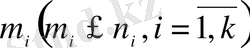 Equation. 3 элемент алсақ, (1. 4) -тің және көбейту ережесінің негізінде мұндай қосылыстардың саны
Equation. 3 элемент алсақ, (1. 4) -тің және көбейту ережесінің негізінде мұндай қосылыстардың саны
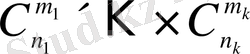
өрнегімен анықталады. Бір ғана
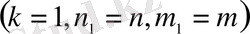 қосылыс үшін бұл өрнек (1. 4) -ке айналады, яғни полиномдық схема биномдық жүйеге ауысады.
қосылыс үшін бұл өрнек (1. 4) -ке айналады, яғни полиномдық схема биномдық жүйеге ауысады.
Қосылыстар теориясынан келтірілген мәліметтер және (1. 1) формуласы урналар тәсілінде ықтималдыықтарды есептеудің комбинациялық әдісінің негізін құрайды.
2-есеп. Сөреге (төртбұрышты) тәуекел қойылған 8 кітаптың қалаулы екеуі қатар орналасуының ықтималдығын табыңыз. 0
Шешу.
Кітаптардың (нөмірленген) реттелген жиынын 8 элементтен жасалған орын ауыстырулар деп қарасақ,
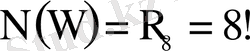 . Сөреде көрші орындардың 7 қосағы бар. Олардың әрқайсысында аталмыш кітаптар екі әдіспен орналаса алады. Қалған кітаптардың орналасу мүмкіндіктерінің саны
. Сөреде көрші орындардың 7 қосағы бар. Олардың әрқайсысында аталмыш кітаптар екі әдіспен орналаса алады. Қалған кітаптардың орналасу мүмкіндіктерінің саны
 Көбейту ережесі бойынша
Көбейту ережесі бойынша
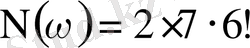 Талап етілген ықтималдық
Талап етілген ықтималдық
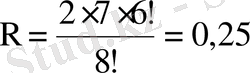 .
.
2-дәріс.
§4. Ықтималдықтарды көбейту формуласы.
Шартты ықтималдық.
Кездейсоқ эксперименттің нәтижесінде пайда болу ықтималдықтары нөлге тең емес:
 >0 болатын A және B оқиғаларының бірі пайда болғанда екіншісінің ықтималдығы өзгермейтін болса, оларды өзара тәуелсіз дейміз. Қалған жағдайларда олар тәуелді болады. Екі оқиғаның тәуелсіздігінің анықтамасы ретінде
>0 болатын A және B оқиғаларының бірі пайда болғанда екіншісінің ықтималдығы өзгермейтін болса, оларды өзара тәуелсіз дейміз. Қалған жағдайларда олар тәуелді болады. Екі оқиғаның тәуелсіздігінің анықтамасы ретінде
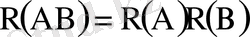 (1. 9)
(1. 9)
теңдігін қабылдауға болады. Бірақ, ол көбіне оқиғалардың тәуелсіздігін тексеруге қолданылады.
Шекті

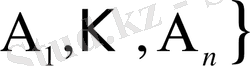 оқиғалар жиынының кез келген m
оқиғалар жиынының кез келген m
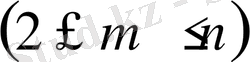 элементінен жасалған теру үшін
элементінен жасалған теру үшін
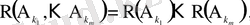
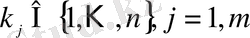 (1. 10)
(1. 10)
болса, бұл оқиғалар жиынтығында тәуелсіз дейміз. Оқиғалардың (n>2) жиынтығында тәуелсіз болуының қажетті шарты олардың қос-қостан тәуелсіз болуында. Жиынтығында тәуелсіз оқиғалар үшін
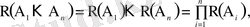
 (1. 11)
(1. 11)
теңдігі (n=2 болғанда (1. 9) ) ықтималдықтарды көбейту формуласы деп аталады.
Тәуелді оқиғалар үшін
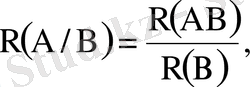
 >0,
>0,
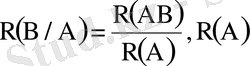 >0 (1. 12)
>0 (1. 12)
саны кездейсоқ эксперименттің нәтижесінде оқиғалардың бірі пайда болғанда екіншісінің де пайда болуының шартты ықтималдығы деп аталады.
Шартты ықтималдықтың бұл аксиомалық түсінігі ықтималдықтың классикалық схемасына қайшы келмейді. Мысалы, тәжірибенің барлық мүмкін n=N(Ω) нәтижесінің A оқиғасының пайда болуына қолайлысы m (m≤n, 4-сурет) десек,

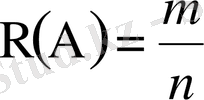 Оқиғаның (A) пайда болуы осы m нәтиженің бірінің іске асқандығын көрсетеді.
Оқиғаның (A) пайда болуы осы m нәтиженің бірінің іске асқандығын көрсетеді.
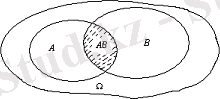
4-сурет
Енді A-мен қатар B оқиғасының пайда болуын қарағанда аталған m нәтиже мүмкіндіктердің жалпы санын құрайды. Солардың ішінде k (k≤m) нәтиже B-ның да, демек, AB оқиғасының да пайда болуына қолайлы болсын. Классикалық жүйе (1. 12) -нің екінші формуласына келтіреді:
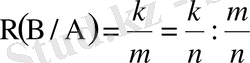
Тәуелсіз оқиғалар үшін
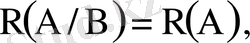
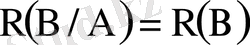
Егер
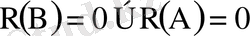 болса, (1. 12) -дегі шартты ықтималдықтар тиісінше анықталмаған болып саналады. Олардың екеуі де анықталған болса, онда тәуелді оқиғалар үшін ықтималдықтарды көбейту формуласы
болса, (1. 12) -дегі шартты ықтималдықтар тиісінше анықталмаған болып саналады. Олардың екеуі де анықталған болса, онда тәуелді оқиғалар үшін ықтималдықтарды көбейту формуласы
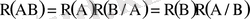 (1. 13)
(1. 13)
түрінде жазылып, оқиғалардың бірге пайда болуының ықтималдығын табу үшін қолданыла алады. Жиынтығында тәуелсіз емес
 оқиғалары үшін (1. 13) -ті жалпы түрде
оқиғалары үшін (1. 13) -ті жалпы түрде
 (1. 14)
(1. 14)
деп жазуға болады.
§5. Ықтималдықтарды қосу теоремасы.
Теорема. Бірікпейтін бірнеше оқиғаның қайсысы бола да біреуінің пайда болуының ықтималдығы олардың ықтималдықтарының қосындысына тең:
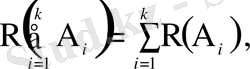
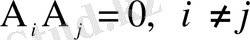 (
(
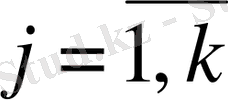 ) (1. 15)
) (1. 15)
Дәлелдеу.
Айталық, кездейсоқ эксперимент үшін
 , соның ішінде
, соның ішінде
 оқиғасының пайда болуына
оқиғасының пайда болуына
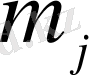 нәтиже қолайлы болсын. Оқиғаларға мүмкін (жиындарға қолданылатын ) амалдар қолдану арқылы алынған оқиғаны күрделі оқиға дейміз. Күрделі
нәтиже қолайлы болсын. Оқиғаларға мүмкін (жиындарға қолданылатын ) амалдар қолдану арқылы алынған оқиғаны күрделі оқиға дейміз. Күрделі
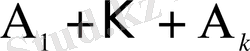 оқиғасы пайда болу үшін қосылғыш оқиғалардың кез келген біреуі пайда болса болғаны, демек, оған
оқиғасы пайда болу үшін қосылғыш оқиғалардың кез келген біреуі пайда болса болғаны, демек, оған
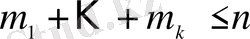 нәтиже қолайлы.
нәтиже қолайлы.
Классикалық схема бойынша
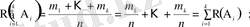
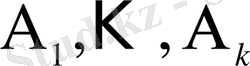 оқиғалары толық топ құрайтын болса,
оқиғалары толық топ құрайтын болса,
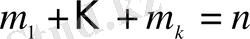 және ықтималдықтардың екінші аксиомасына сай
және ықтималдықтардың екінші аксиомасына сай
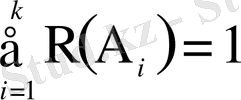 . Әдетте (1. 15) ықтималдықтарды қосу аксиомасы (үшінші аксиома) деген атпен дәлелдеусіз қабылданады.
. Әдетте (1. 15) ықтималдықтарды қосу аксиомасы (үшінші аксиома) деген атпен дәлелдеусіз қабылданады.
Бірікпейтін
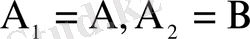 (k=2) оқиғалары үшін ω(A) және ω(B) жиындары қиылыспайды (айқаспайды) :
(k=2) оқиғалары үшін ω(A) және ω(B) жиындары қиылыспайды (айқаспайды) :
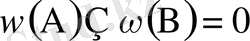 . Екі жиынның да барлық элементтері
. Екі жиынның да барлық элементтері
 оқиғасының пайда болуына қолайлы, олардың ортақ элементтері жоқ: (1. 15)
оқиғасының пайда болуына қолайлы, олардың ортақ элементтері жоқ: (1. 15)
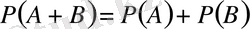 түрінде жазылады. Ал, бірігетін оқиғалар үшін
түрінде жазылады. Ал, бірігетін оқиғалар үшін
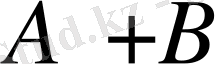 оқиғасының пайда болуына қолайлы нәтижелердің санын анықтағанда
оқиғасының пайда болуына қолайлы нәтижелердің санын анықтағанда
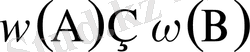 аймағына сай келетін нәтижелер қайталанып алынбас үшін ықтималдықтарды қосу теоремасын
аймағына сай келетін нәтижелер қайталанып алынбас үшін ықтималдықтарды қосу теоремасын
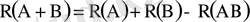 (1. 16)
(1. 16)
түрінде жазамыз.
Бірігетін n оқиға үшін ықтималдықтарды қосудың жалпыланған формуласы
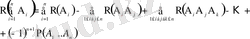
(1. 17)
түрінде жазылады. Қосылғыштардың саны өскен сайын оны қолдану күрделі есептеулерді талап етеді. Мысалы, бірігетін үш оқиғаның кем дегенде біреуінің пайда болу ықтималдығы
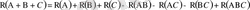 (1. 18)
(1. 18)
Оқиғалардың толық тобын құру арқылы есептеуді азайтуға болады. Қарама-қарсы оқиғалар қашанда толық топ құрайды:
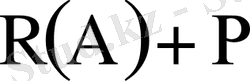 (Ā) =p+q=1 (1. 19)
(Ā) =p+q=1 (1. 19)
Бұл шарт
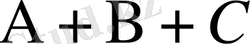 және
және

 қарама-қарсы оқиғалары үшін де орындалады, демек,
қарама-қарсы оқиғалары үшін де орындалады, демек,
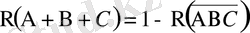 Жалпы түрде
Жалпы түрде
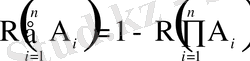 . (1. 20)
. (1. 20)
Қаралып отырған оқиғалар жиынтығында тәуелсіз болса:
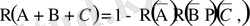
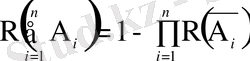 (1. 21) .
(1. 21) .
§6. Толық ықтималдық формуласы.
Байес формулалары.
Белгілі бір кедейсоқ эксперименттің нәтижесінде байқалатын A оқиғасы сол тәжірибенің толық топ құрайтын, A-ға қарағанда гипотезалар (болжамдар) деп аталатын
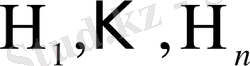 нәтижелерінің бірімен ғана қосарласа пайда бола алсын. Болжамдардың шартсыз ықтималдықтарын :
нәтижелерінің бірімен ғана қосарласа пайда бола алсын. Болжамдардың шартсыз ықтималдықтарын :
 >0 классикалық тәсіл бойынша тәжірибеге дейін (априорлық түрде) анықтауға болады. Болжамдар қос-қостан бірікпейтін болғандықтан
>0 классикалық тәсіл бойынша тәжірибеге дейін (априорлық түрде) анықтауға болады. Болжамдар қос-қостан бірікпейтін болғандықтан
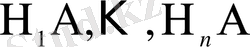 күрделі оқиғалары да сол шартты қанағаттандырады. Соңғылардың ықтималдықтарының қосындысы
күрделі оқиғалары да сол шартты қанағаттандырады. Соңғылардың ықтималдықтарының қосындысы
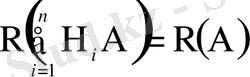
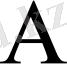 оқиғасының толық ықтималдығы деп аталады. Оны ықтималдықтарды қосу аксиомасының (1. 15) және ықтималдықтарды көбейту формуласының (1. 13) көмегімен табуға болады. Бізге болжамдардың қайсысы іске асса да бәрі бір, тек A оқиғасы пайда болса болғаны. Сондықтан
оқиғасының толық ықтималдығы деп аталады. Оны ықтималдықтарды қосу аксиомасының (1. 15) және ықтималдықтарды көбейту формуласының (1. 13) көмегімен табуға болады. Бізге болжамдардың қайсысы іске асса да бәрі бір, тек A оқиғасы пайда болса болғаны. Сондықтан
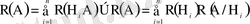 (1. 22)
(1. 22)
Соңғы теңдік толық ықтималдық формуласы деп аталады.
Енді тәжірибе өткізіліп,
 оқиғасының пайда болғаны белгілі болды делік. Бұл
оқиғасының пайда болғаны белгілі болды делік. Бұл
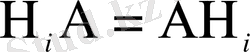
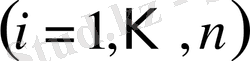 күрделі оқиғаларының да бірі пайда болды деген сөз; (1. 13) бойынша
күрделі оқиғаларының да бірі пайда болды деген сөз; (1. 13) бойынша
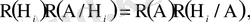
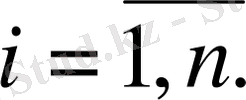
Бұдан болжамдардың тәжірибеден кейінгі (апостериорлық) ықтималдықтары
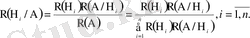 (1. 23)
(1. 23)
Байес формулалары деп аталатын бұл теңдіктер бақыланып отырған A оқиғасының пайда болғаны туралы ақпарат алынғаннан кейін әрбір болжамның орындалу ықтималдығын есептеуге (тексеруге) мүмкіндік береді.
2-тарау. Тәуелсіз сынақтар тізбегі.
3-дәріс.
§1 Ықтималдықтардың биномдық үлестірілуі.
Сынақтар бірдей жағдайда көп-көптен еселеп қайталанатын тәжірибелерде де бірқатар маңызды заңдылықтар байқалады. Егер A оқиғасының (нәтижесінің) әрбір сынақта пайда болу ықтималдығы басқа сынақтардың нәтижелерінен тәуелсіз болса, онда сынақтар тізбегі A оқиғасына қарағанда тәуелсіз дейміз. Қайталанба тәуелсіз сынақтардың қарапайым класы ретінде әрбір сынақта оқиғаның пайда болу ықтималдығы тұрақты екі-ақ нәтижесі бар (биномдық жүйе) : A-табыс,
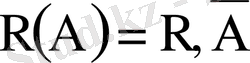 -табыссыздық,
-табыссыздық,
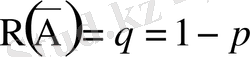 сынақтардың тізбегін алуға болады. Мұндай сынақтардың көрнекті мысалдары:1) теңге үйіру. Мұнда, айталық, елтаңбаның (гербтың) түсуі-табыс, цифрдың (тордың) түсуі табыссыздық және
сынақтардың тізбегін алуға болады. Мұндай сынақтардың көрнекті мысалдары:1) теңге үйіру. Мұнда, айталық, елтаңбаның (гербтың) түсуі-табыс, цифрдың (тордың) түсуі табыссыздық және
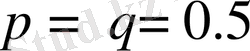 . 2) нысанаға оқ ату: тигізу-табыс, мүлт кету-табыссыздық т. с. с.
. 2) нысанаға оқ ату: тигізу-табыс, мүлт кету-табыссыздық т. с. с.
Тәуелсіз
 сынақ топтамасында
сынақ топтамасында
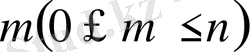 рет табысқа ие болу ықтималдығын
рет табысқа ие болу ықтималдығын
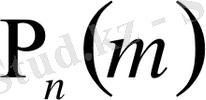 табалық. Топтамадағы сынақтарды ретінше
табалық. Топтамадағы сынақтарды ретінше
 номірлерімен, ал табыс келтірген сынақтарды
номірлерімен, ал табыс келтірген сынақтарды
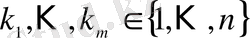 сандарымен белгілеп, оларды сәйкес Ω және ω жиындарының элементтері ретінде қаралық. Бізге A оқиғасы сынақтар топтамасында дәл m рет пайда болса болғаны, табыс әкелген сынақтардың рет санын ескермеуге болады. Сондықтан m рет табысқа ие болудың барлық мүмкін жағдайларының саны n элементтен m-нен жасалған терулердің санымен
сандарымен белгілеп, оларды сәйкес Ω және ω жиындарының элементтері ретінде қаралық. Бізге A оқиғасы сынақтар топтамасында дәл m рет пайда болса болғаны, табыс әкелген сынақтардың рет санын ескермеуге болады. Сондықтан m рет табысқа ие болудың барлық мүмкін жағдайларының саны n элементтен m-нен жасалған терулердің санымен
 анықталады. Олардың әрқайсысында
анықталады. Олардың әрқайсысында
 оқиғасы m рет,
оқиғасы m рет,
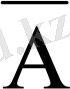 оқиғасы
оқиғасы
 рет пайда болып, ықтималдықтары
рет пайда болып, ықтималдықтары
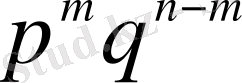 бірдей
бірдей
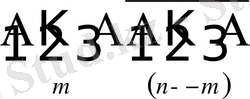 түріндегі күрделі оқиға орын алады. Ықтималдықтарды қосу аксиомасының негізінде Бернулли формуласы деп аталатын
түріндегі күрделі оқиға орын алады. Ықтималдықтарды қосу аксиомасының негізінде Бернулли формуласы деп аталатын
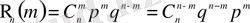 (2. 1)
(2. 1)
теңдігіне келеміз. Натурал аргумент функциясының
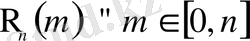 мәндерінің жиыны қайталанба тәуелсіз сынақтарда ықтималдықтардың биномдық үлестірілуі (Бернулли үлестірілуі) деп аталады. Барлық n сынақта табыс санының мүмкін мәндері
мәндерінің жиыны қайталанба тәуелсіз сынақтарда ықтималдықтардың биномдық үлестірілуі (Бернулли үлестірілуі) деп аталады. Барлық n сынақта табыс санының мүмкін мәндері
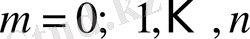 толық топ құрайтындықтан ықтималдықтардың екінші аксиомасы бойынша
толық топ құрайтындықтан ықтималдықтардың екінші аксиомасы бойынша
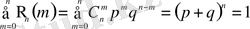 (2. 2)
(2. 2)
Қарапайым түрлендірулердің көмегімен
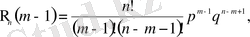
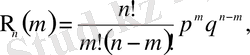
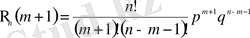
шамаларының арасындағы байланысты табуға болады. Атап айтқанда:
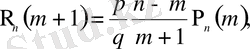
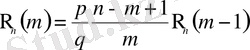 (2. 3)
(2. 3)
Бұл балама қатынастар биномдық ықтималдықтар үшін реккуренттік формула деген атпен белгілі.
«Дискретті үлгідегі»
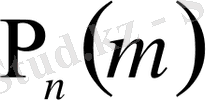 функциясының мәндер жиынында n+1 сан бар. Оның
функциясының мәндер жиынында n+1 сан бар. Оның
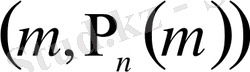 нүктелерін түзу кесінділермен қосу арқылы тұрғызылған «графигі»
нүктелерін түзу кесінділермен қосу арқылы тұрғызылған «графигі»
(5, 6-суреттер) ықтималдықтардың үлестірілу көпбұрышы деп аталатын жазық сынық сызық болады. Аргументтің ең үлкен ықтималдық
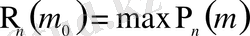 сай келетін
сай келетін
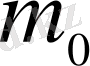 мәні A оқиғасының n тәуелсіз сынақтар топтамасында пайда болуының ең
мәні A оқиғасының n тәуелсіз сынақтар топтамасында пайда болуының ең
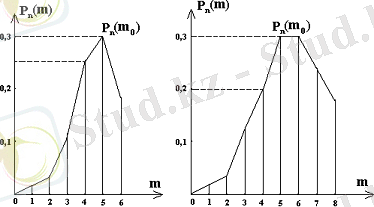
5-сурет 6-сурет
ықтимал саны деп аталады. Анықтама бойынша:
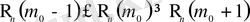 .
.
Бұл қос теңсіздіктің әрқайсысын рекуренттік формуланың (2. 3) көмегімен шешіп, табыстың ең ықтимал саны орналасқан кесіндіні табамыз:
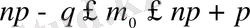
Кесіндінің ұзындығы
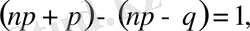 ал
ал
 болғандықтан
болғандықтан
 санының бүтін бөлігі -
санының бүтін бөлігі -
 функциясының белгілеуін пайдаланып,
функциясының белгілеуін пайдаланып,
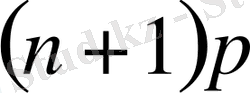 бөлшек сан болғанда
бөлшек сан болғанда
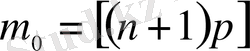 (2. 4)
(2. 4)
деп жаза аламыз.
Осылайша анықталғын натурал сан
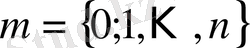 шамасының модасы деп аталады. Егер
шамасының модасы деп аталады. Егер
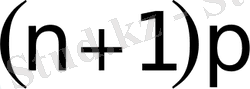 бөлшек сан болса, онда
бөлшек сан болса, онда
 нің осы санның бүтін бөлігіне тең бір ғана мәні бар және биномдық үлестірілуді унимодалы дейміз. Ал,
нің осы санның бүтін бөлігіне тең бір ғана мәні бар және биномдық үлестірілуді унимодалы дейміз. Ал,
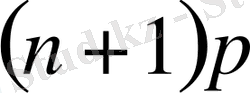 , демек,
, демек,
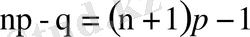 де бүтін сан болса, онда оның екеуі де
де бүтін сан болса, онда оның екеуі де
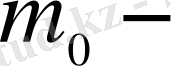 нің мәні бола алады. Бұл жағдайда үлестірілуді бимодалы деуге болар еді.
нің мәні бола алады. Бұл жағдайда үлестірілуді бимодалы деуге болар еді.
Сонымен,
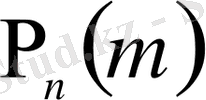 функциясы
функциясы
 кесіндісінің сол жақ «жартысында» өспелі, оң жақ «жартысында» кемімелі. Ал,
кесіндісінің сол жақ «жартысында» өспелі, оң жақ «жартысында» кемімелі. Ал,
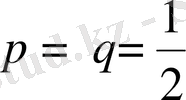 (теңге үйіру) болғанда биномдық коэффициенттердің симметриялық қасиеті салдарынан
(теңге үйіру) болғанда биномдық коэффициенттердің симметриялық қасиеті салдарынан
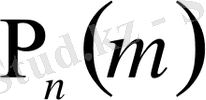 функциясының графигі бұл жағдайда
функциясының графигі бұл жағдайда
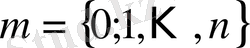 шамасының медианасы деп аталатын «
шамасының медианасы деп аталатын «
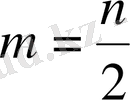 түзуіне» қарағанда симметриялы болады; (2. 2) теңдігі табаны
түзуіне» қарағанда симметриялы болады; (2. 2) теңдігі табаны
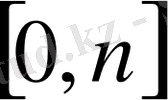 кесіндісі болатын, жоғарыдан ықтималдықтардың үлестірілу көпбұрышымен шектелген фигура ауданының бірге тең екенін көрсетеді. Медиана осы ауданды қақ бөледі.
кесіндісі болатын, жоғарыдан ықтималдықтардың үлестірілу көпбұрышымен шектелген фигура ауданының бірге тең екенін көрсетеді. Медиана осы ауданды қақ бөледі.
Ықтималдықтардың биномдық үлестірілуі тәуелсіз сынақтар топтамасында біз мүдделі болып отырған оқиғаның мөлшерлі рет пайда болуының ықтималдығын ғана емес, табыс санының
 берілген шекараларда (мысалы,
берілген шекараларда (мысалы,
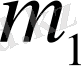 және
және
 ) жатуының:
) жатуының:
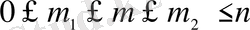 ықтималдығын табуға да мүмкіндік береді. Интервалдық ықтималдық деп аталатын бұл шаманы табу үшін ықтималдықтарды қосу аксиомасын пайдаланып, (2. 1) өрнегінің
ықтималдығын табуға да мүмкіндік береді. Интервалдық ықтималдық деп аталатын бұл шаманы табу үшін ықтималдықтарды қосу аксиомасын пайдаланып, (2. 1) өрнегінің
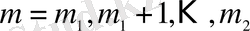 болғандағы мәндерінің қосындысын анықтасақ жеткілікті:
болғандағы мәндерінің қосындысын анықтасақ жеткілікті:
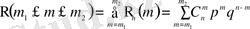 (2. 5)
(2. 5)
Бұл n тәуелсіз сынақта A оқиғасының пайда болу санының берілген
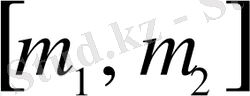
аралығында жатуының ықтималдығы;
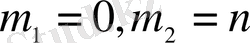 болғанда (2. 2) бойынша
болғанда (2. 2) бойынша
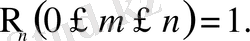 Егер (2. 5) өрнегінде қосылғыштар саны көп болса, есептеуді жеңілдету үшін оқиғалардың толық тобын, қарама-қарсы оқиғалар системасын құруға болады. Мысалы,
Егер (2. 5) өрнегінде қосылғыштар саны көп болса, есептеуді жеңілдету үшін оқиғалардың толық тобын, қарама-қарсы оқиғалар системасын құруға болады. Мысалы,
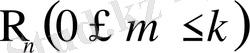 -ны табу керек және
-ны табу керек және
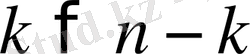 болса, онда
болса, онда
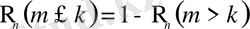 (2. 6)
(2. 6)
теңдігін пайдаланған тиімді.
Енді тәуелсіз сынақтар тізбегінің полиномдық жүйесін қарастыралық. Мұнда әрбір сынақтың толық топ құрайтын, пайда болу ықтималдықтары
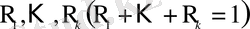 топтамада өзгермейтін
топтамада өзгермейтін
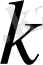 нәтижесі-
нәтижесі-
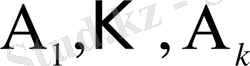 оқиғалары болады. Құрама нәтиженің- n сынақта
оқиғалары болады. Құрама нәтиженің- n сынақта
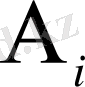 оқиғасы
оқиғасы
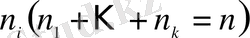 рет пайда болуының ықтималдығы
рет пайда болуының ықтималдығы
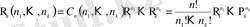 (2. 7)
(2. 7)
Бұл Бернулли формуласының жалпыланған түрі;
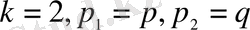 болғанда полиномдық үлестірілудің ықтималдығы (2. 7) биномдық үлестірілу ықтималдығына (2. 1) айналады.
болғанда полиномдық үлестірілудің ықтималдығы (2. 7) биномдық үлестірілу ықтималдығына (2. 1) айналады.
4-дәріс.
§2 Лапластың локальдық теоремасы.
Биномдық үлестірілудің асимптоталық формулалары.
Сынақтардың саны n өскен сайын Бернулли формуласын қолдануда есептеу қиындықтары арта түседі. Сондықтан француз ғалымдары: 1730 жылы Муавр
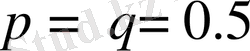 жағдайы үшін, кейін Лаплас кез келген
жағдайы үшін, кейін Лаплас кез келген
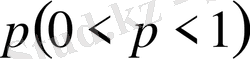 үшін (2. 1) -дің орнына
үшін (2. 1) -дің орнына
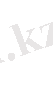 σ
σ
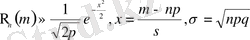 (2. 8)
(2. 8)
жуық формуласын қолдануға болатынын дәлелдеді. Мұнда
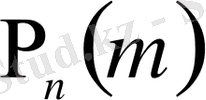 ықтималдығы аргументтің x, демек, тәуелсіз сынақтар топтамасындағы табыс санының m жеке («локальдық-жергілікті») мәні үшін ғана анықталады. Анықталу дәлдігі
ықтималдығы аргументтің x, демек, тәуелсіз сынақтар топтамасындағы табыс санының m жеке («локальдық-жергілікті») мәні үшін ғана анықталады. Анықталу дәлдігі
 өскен сайын арта түседі. Сондықтан (2. 8) математикалық әдебиетте биномдық үлестірілудің асимптоталық формуласы, ал оның мазмұны Муавр- Лапластың локальдық теоремасы деген атпен белгілі. Мұндағы
өскен сайын арта түседі. Сондықтан (2. 8) математикалық әдебиетте биномдық үлестірілудің асимптоталық формуласы, ал оның мазмұны Муавр- Лапластың локальдық теоремасы деген атпен белгілі. Мұндағы
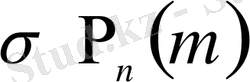 өрнегі ықтималдық функциясы деп аталып,
өрнегі ықтималдық функциясы деп аталып,
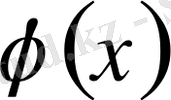 арқылы белгіленеді. Оның графигін ықтималдық қисығы дейміз. Қолдануды жеңілдету үшін
арқылы белгіленеді. Оның графигін ықтималдық қисығы дейміз. Қолдануды жеңілдету үшін
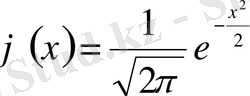 (2. 9)
(2. 9)
функциясы мәндерінің кестесі түзілген. Кестенің не графиктің көмегімен
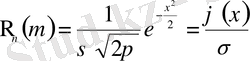 (2. 10)
(2. 10)
ықтималдығын жуықтап табуға болады.
Ықтималдық функциясын
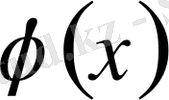 аналитикалық әдістермен зерттеп, оның қасиеттерін анықтап, ықтималдық қисығын тұрғызуға болады.
аналитикалық әдістермен зерттеп, оның қасиеттерін анықтап, ықтималдық қисығын тұрғызуға болады.
Функция бүкіл сандық осьте анықталған:
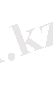
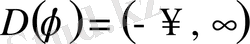 , жұп:
, жұп:
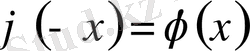 , оң таңбалы:
, оң таңбалы:
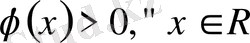 . Графигі жоғарғы жарты жазықтықта жатыр, ордината осіне қарағанда симметриялы (7-сурет) .
. Графигі жоғарғы жарты жазықтықта жатыр, ордината осіне қарағанда симметриялы (7-сурет) .
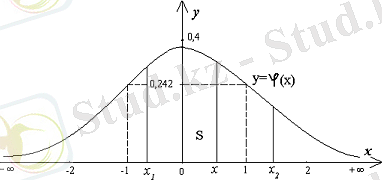
. 7-сурет
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz