Эллипс тектес теңдеулерді шекті айырымдар және шекті элементтер әдістерімен шешудің мүмкіндіктерін зерттеу

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Қожа Ахмет Ясауи атындағы халықаралық қазақ-түрік университеті

Математика кафедрасы

Қорғауға жіберілді
Кафедра меңгерушісі
_______профессор Ә.С.Мұратов

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: Эллипс тектес теңдеулерді шекті айырымдар және шекті
элементтер әдістерімен шешудің мүмкіндіктерін
зерттеу

5В010900 – Математика мамандығы бойынша

Орындаған
Бөлкенова Б.

Ғылыми жетекшісі
тех.ғ.к., доцент
Айтбаев Қ.

Түркістан 2013
МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . ... ... ... ... 3
1 ЭЛЛИПС ТЕКТЕС ТЕҢДЕУЛЕРДІҢ ЕСЕПТЕРІН АНАЛИТИКАЛЫҚ ӘДІСТЕРМЕН
ШЕШУДІҢ ТЕОРИЯСЫ ... 5
1.1 Математикалық физика 5
теңдеулері ... ... ... ... ... ... ... ... ... ... ... ...
1.2 Эллипстік теңдеулер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 6
1.2.1Лаплас 6
теңдеуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
...
1.2.2Пуассон 10
теңдеуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... .
1.3 Шекаралық және бастапқы 15
шарттар ... ... ... ... ... ... ... ... . ... ... ...
1.3.1Шекаралық 16
шарттар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
1.3.2Бастапқы 18
шарттар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
2 ЭЛЛИПСТІК ТЕҢДЕУЛЕРДІҢ ЕСЕПТЕРІН ШЕКТІ АЙЫРЫМДАР ӘДІСІМЕН ШЕШУ
... ... ... ... ... ... ... ... ... .. 19
2.1 Пуассонның бірөлшемді теңдеуін шекті айырымдар әдісімен шешу
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...19
... ... ... ... ..
2.2 Пуассонның екіөлшемді теңдеуін шекті айырымдар әдісімен
шешу ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ...20
... ... ... ... ... ... ... ... .. ... ... ...
3 ЭЛЛИПС ТЕКТЕС ТЕҢДЕУЛЕРДІ ШЕКТІ ЭЛЕМЕНТТЕР
ӘДІСІМЕН ШЕШУ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 29
3.1 Шекті элементтер әдісінің негізгі концепциясы 29
... ... ... ... ... ... ...
3.2 Тұтас жазық денедегі температуралық өрісті шекті элементтер
әдісімен зерттеудің теориялық 33
негіздері ... ... ... ... ... ... ... ... ... ...
3.3 Негізгі функционалдың құрамындағы интегралдарды есептеуді
автоматтандыру 41
жолдары ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
3.4 Автомобиль жолдарының көпқабатты құрылымының температуралық күйін
анықтау есебінің қойылымы ... ... ... ... ... . 54
3.5 Жол құрылымының температуралық күйінің жыл мезгілдеріне
байланысты өзгеру заңдылықтарын зерттеу 57
... ... ... ... ... ... ... ... ..
ҚОРЫТЫНДЫ ... ... ... ... ... ... . ... ... ... ... ... ... ... ...63
... ... ... ... ... ... ... ...
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР 64
ТІЗІМІ ... ... ... ... ... ... ... ... ...

КІРІСПЕ

Математикалық физика теңдеулерінің ішінде эллипс тектес теңдеулердің
алатын орны ерекше екені белгілі. Қоршаған ортада жиі кездесетін құбылыстар
ретінде тұтас денелердегі жылу таралу процестері, диффузия, электрлік
статика, электрлік динамика, сұйықтардың ағысы, электр тогының тығыздығының
таралуы, қатты денелердің деформациялануы және тағы басқаларын атайтын
болсақ, осы құбылыстарды зерттеу үшін математикалық физика есептері
қойылып, эллипс текті Лаплас, немесе Пуассон теңдеулері шешіледі. Зерттеу
аймағы біртекті және оның пішіні қарапайым болған кезде аталған теңдеулерді
Фурье әдісі, Грин функциялары әдісі және т.б. аналитикалық әдістермен
шешуге болады. Бірақ көп жағдайда аталған есептердің дәл аналитикалық
шешімін алу үшін шекаралық шарттарды аналитикалық өрнектермен сипаттауға
ыңғайлы болу мақсатында көптеген жеңілдетуші гипотезалар енгізіледі. Соның
өзінде зерттеу аймағының біртекті болуы және геометриясы қарапайым болуы
ыңғайлы. Математикалық физиканың дербес туындылы дифференциалдық
теңдеулермен, немесе олардың жүйелерімен сипатталатын күрделі есептерін
шешу үшін әдетте вариациялық принциптерді қолданып, аталған теңдеулерді
сандық әдістердің бірімен сызықтық алгебралық теңдеулер жүйесіне алып
келеді. Зерттеу аймағы біртекті болмаған жағдайда, және зерттеу аймағының
геометриясы күрделі болған жағдайда сандық әдістердің ішіндегі ең әмбебап
әдіс деп табылатын әдіс – шекті элементтер әдісі таңдалады. Алынған жоғары
ретті сызықтық алгебралық теңдеулер жүйесін шешуге тікелей немесе
итерациялық әдістер қолданылады. Бұл кездегі ең қиын проблемалардың бірі
есептеу процесінің жинақтылығын қамтамасыз ету. Шешімнің дәлдігі
координаталық тордың қадамына, итерация санына және компьютердің қуатына
байланысты.
Дипломдық жұмыста математикалық физиканың негізгі теңдеулері,
шекаралық және бастапқы шарттарды берудің ерекшеліктері, эллипс тектес
тедеулерді шекті айырымдар әдісімен шешу алгоритмы, дербес туындылы
дифференциалдық теңдеулерді дискреттеу әдістері, шекті элементтер әдісінің
теориялық негіздері, шекті элементтер әдісін қолданып жылуөткізгіштік,
кернеулі-деформациялық күй туралы есептерді шығарудың негізгі этаптары
сияқты тақырыптар қамтылған.
Дипломдық жұмыс кiрiспеден, үш бөлімнен тұратын негiзгi бөлiктен,
қорытындыдан және пайдаланылған әдебиеттер тiзiмiнен тұрады.
Бірінші бөлімде математикалық физика теңдеулеріне сараптама
жүргізіледі. Эллипстік, параболалық және гиперболалық теңдеулердің түрлері
және олармен сипатталатын физикалық процестерге талдау жасалынады. Келесі
бөлімде математикалық физика теңдеулерін шешуде кеңінен қолданылып жүрген
сандық әдіс, шекті айырымдар әдісінің бір өлшемді және екі өлшемді Пуассон
теңдеулерін шешуге арналған алгоритмдері келтіріліп, алгоритмдердің MATLAB
жүйесінде құрылған есептеу программаларына түсініктемелер келтірілген.
Үшінші бөлім эллипс тектес теңдеулерді шекті элементтер әдісімен
шешуге арналған. Бөлімнің басында шекті элементтер әдісінің теориялық
негіздері келтіріледі. Әдістің негізгі этаптары, оның негізгі концепциясы,
артықшылығы мен кемшіліктері талданады. Аймақты дискреттеудің ережелері
қарастырылады. Үшінші бөлімнің келесі жартысында математикалық физика
ғылымында қарастырылатын негізгі есептердің бірі, жылу таралу есебінің
теориясы және оны шешуде қолданылатын шекті элементтер әдісінің алгоритмі
келтірілген. Бөлімнің соңында, мысал ретінде, екіөлшемді жылу таралу
есебінің шешу жолдары көрсетіліп, сандық нәтижеге дейін жеткізілген.
Дипломдық жұмыста математикалық физиканың кез келген есебін сандық
әдістер, шекті айырымдар әдісі мен шекті элементтер әдісі арқылы шешудің
әдістемесінің негізі қаланған деп айтуға болады.

1 ЭЛЛИПС ТЕКТЕС ТЕҢДЕУЛЕРДІҢ ЕСЕПТЕРІН
АНАЛИТИКАЛЫҚ ӘДІСТЕРМЕН ШЕШУДІҢ ТЕОРИЯСЫ

1.1 МАТЕМАТИКАЛЫҚ ФИЗИКА ТЕҢДЕУЛЕРІ

Қазіргі заманда ғылым мен техниканың көптеген мәселелері
математикалық физика есептерін шешумен байланысты. Жылуөткізгіштік,
диффузия, электрлік статика, электрлік динамика, сұйықтардың ағысы, электр
тогының тығыздығының таралуы, қатты денелердің деформациялануы және тағы
басқа көптеген есептер математикалық физика есептеріне жатады.
Мұндай есептер шекаралық және бастапқы шарттармен бірге
қарастырылатын дербес туындылы дифференциалдық теңдеулермен сипатталады.
Дипломдық жұмыста қарастырылатын дифференциалдық теңдеулердің реті
екіншіден аспайды. Себебі, осындай теңдеулер сипаттайтын физикалық
құбылыстардың өзі өте үлкен диапазон құрайды. Оның үстіне, төменде
келтірілетін әдістерді бұдан да жоғары ретті дифференциалдық теңдеулерге
қолдануға болады. Жалпы жағдайда n тәуелсіз айнымалының екінші реттегі
дербес туындылы дифференциалдық теңдеуі мынадай түрде болады [1,2]:

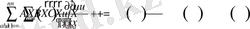. (1.1)

Бұл жерде 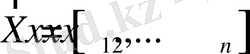– тәуелсіз айнымалылардың векторы (матрица-қатар); –
тәуелсіз айнымалылардың белгісіз функциясы; – тәуелсіз айнымалылардың
белгілі функциялары.
(1.1) - ші теңдеуді үш стандартты канондық түрлердің біреуіне
әрқашанда келтіруге болады. 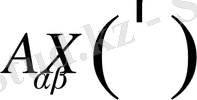шамаларының өзара қатынасына байланысты
теңдеулерді 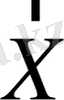нүктесіндегі эллипстік, параболалық немесе гиперболалық
текті теңдеу деп бөледі. Мысалы, тәуелсіз 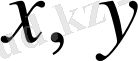айнымалыларының екінші
ретті дифференциалдық

(1.2)

теңдеуінің тегі дискриминант деп аталатын келесі шаманың мәні арқылы
анықталады:

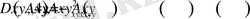. (1.3)

Егер 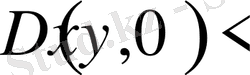болса, онда дифференциалдық теңдеу 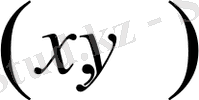нүктесінде
эллипстік теңдеу болады.
Егер 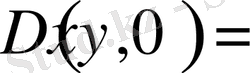болса, онда дифференциалдық теңдеу 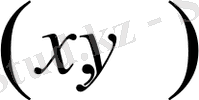нүктесінде
параболалық теңдеу болады.
Егер 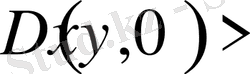болса, онда дифференциалдық теңдеу 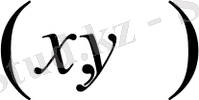нүктесінде
гиперболалық теңдеу болады.
Егер 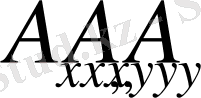коэффициенттері тұрақты болса және дискриминант
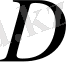координатаға тәуелсіз болса, онда дискриминанттың таңбасына байланысты
теңдеу толық эллипстік, толық параболалық немесе толық гиперболалық болып
бөлінеді [1].

1.2 ЭЛЛИПСТІК ТЕҢДЕУЛЕР

Математикалық физиканың эллипстік теңдеулерге алып келетін кейбір
есептерін қарастырайық.

1. ЛАПЛАС ТЕҢДЕУІ

Көптеген стационар, уақытқа тәуелсіз, процестер эллипс текті
теңдеулермен сипатталады. Ал қарапайым жағдайда, біртекті ортада нүктелік
немесе сызықтық әсер көздері жоқ болса процесс координатаның үш бағыты үшін
Лаплас теңдеуімен [2] сипатталады:

.
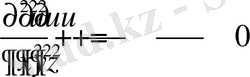(1.4)

Бұл жерде – анықталатын белгісіз функция.
Операторлық түрде Лаплас теңдеуі былайша жазылады:

.
(1.5)

Бұл жерде 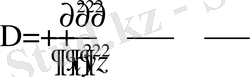– Лаплас операторы.
Енді 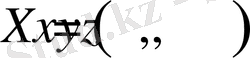үшөлшемді кеңістіктің 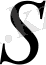тұйық бетімен қоршалған
көлемінде стационар режимде жылудың таралуы туралы есепті қарастырайық.
Жылуөткізгіштік процесі, немесе кондукция, Фурье заңымен анықталады.
Фурье заңы бойынша жылу ағынынының тығыздық векторы
температураның градиентіне пропорционал [1]:

.
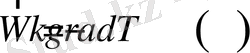(1.6)

Бұл жерде 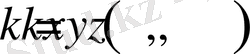– жылуөткізгіштік коэффициенті.
Жылу ағынының тығыздығы уақыттың бір өлшемінде изотермикалық беттің
бірлік ауданынан ағып өтетін жылу мөлшеріне тең [1].
Жылуөткізгіштіктің стационар есебінің мақсаты жылу көздерінің
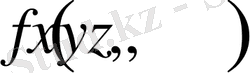тығыздығы белгілі болған жағдайда температураның 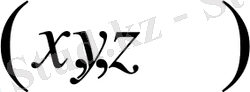координаталарға
тәуелділігін табу. Жылу көздерінің 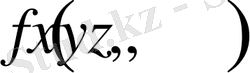тығыздығы (1.6) Фурье теңдеуінің
құрамына тікелей кірмейтін болғандықтан, алдын ала түрлендірулер жасап алу
керек. Жоғарыда келтірілген жылу ағынының анықтамасына сәйкес көлемді
қоршап тұрған бет арқылы уақыттың бір өлшемінде ағып өтетін толық
жылу мөлшері жалпы жағдайда мынадай интегралмен анықталады:

.
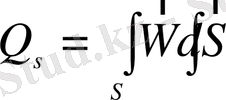(1.7)

Бұл жерде 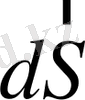ауданы 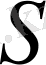бетінің шексіз шағын 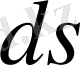элементінің
ауданына тең, бағыты осы элементтің нормалымен бағыттас вектор; –
және 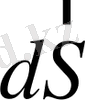векторларының скаляр көбейтіндісі, ал осы
векторлардың арасындағы бұрыш.
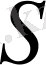бетімен қоршалған көлемінің уақыттың бір өлшемінде бөліп
шығаратын толық жылу мөлшері мынадай интегралмен анықталады:

.
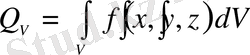(1.8)

Әрине, бұл жағдайда көлемді қоршап тұрған 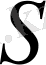бет арқылы
уақыттың бір өлшемінде ағып өтетін толық жылу мөлшері осы көлемнен
бөлініп шығатын толық жылу мөлшеріне тең болуы керек:

.
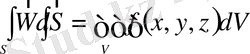(1.9)

Остроградский-Гаусс теоремасы бойынша:

.
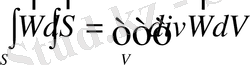(1.10)

Енді (1.10) формуланы (1.9) формулаға қойсақ:

;
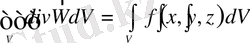(1.11)
.
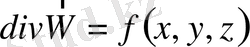(1.12)

(1.12) теңдеуге (1.6) Фурье заңын қойсақ жылуөткізгіштіктің стационар
есебінің теңдеуін векторлық түрде аламыз:

.
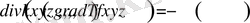(1.13)

Егер жылу көздері жоқ болса 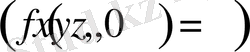және дене біртекті болса ,
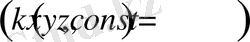онда (1.13) теңдеу былайша жазылады:

.
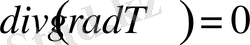(1.14)

Анықтама бойынша кезкелген скалярлық өрістің градиенті былайша

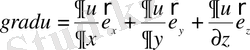(1.15)

жазылатынын, ал кезкелген векторлық 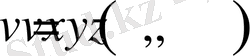өрістің дивергенциясы

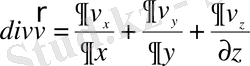(1.16)

өрнегі арқылы анықталатынын ескерсек, онда (1.14) теңдеуді дербес туындылар
арқылы былайша жазып шығуға болады:

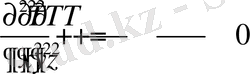(1.17)

немесе операторлық түрде

.
(1.18)

Соңғы (1.18) теңдеу Лаплас теңдеуі деп аталады.
Заттың диффузия процесі көп жағдайда жылуөткізгіштік процессіне ұқсас
келеді. Диффузияны сипаттаған кезде Фурье заңының баламасы - Нернст заңы
қолданылады. Бұл заң бойынша зат ағынының тығыздығының векторы
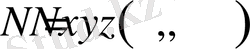концентрацияның градиентіне пропорционал [2]:

.
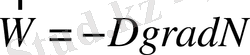(1.19)

Бұл жерде – диффузия коэффициенті.
Зат ағынының тығыздығы уақыттың бір өлшемінде беттің бірлік ауданынан
диффундирленетін заттың бөлшектерінің (атомдар, молекулалар) мөлшеріне тең.
Заттың диффундирленетін көзі жоқ болса 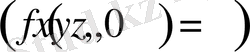және дене біртекті болса
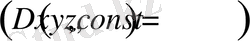, онда (19) өрнекті (12) теңдеуге қойып Лаплас теңдеуін векторлық
түрде аламыз:

.
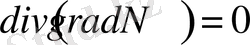(1.20)

Осы теңдеуді дербес туындылар түрінде:

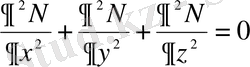(1.21)

немесе операторлық түрде жазсақ:

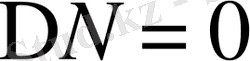(1.22)

Лаплас теңдеуін аламыз.
Лаплас теңдеуіне көптеген есептер, мысалы, электр заряды жоқ кездегі
біртекті өткізбейтін ортада электростатикалық өрістің таралуы туралы есеп
алып келеді. Бұл есеп жалпы түрде Максвелл теңдеулерімен сипатталады:

;
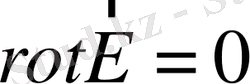(1.23)
.
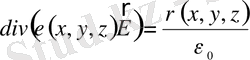(1.24)

Бұл жерде 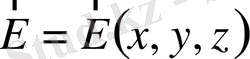электр өрісінің кернеулігінің векторы; 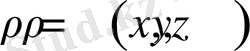– электр
зарядтарының көлемдік тығыздығы; 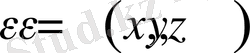– ортаның диэлектрлік өткізгіштігі;
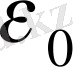– электрлік тұрақты шама. (1.23) теңдеу құйындық электр өрістерінің
жоқ екенін көрсетеді.
Егер ток өткізбейтін орта біртекті болса 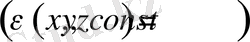және көлемде электр
зарядтары жоқ немесе тепе-тең қалыпта болса, онда (1.24)-ші теңдеу былайша
жазылады:

.
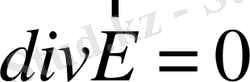(1.25)

Электр өрісінің 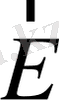кернеулігі электр потенциалымен мынадай
байланыста [1,3]

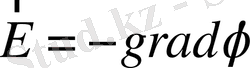(1.26)

болғандықтан (1.26) теңдікті (1.5), (1.15) және (1.16) өрнектерін ескере
отырып (1.25) теңдікке қойсақ, онда Лаплас теңдеуін векторлық түрде
аламыз:

.
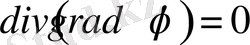(1.27)

Бұл теңдеу дербес туындылар түрінде былайша:

,
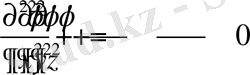(1.28)

ал операторлық түрде былайша:

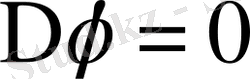(1.29)

жазылады.

1.2.2 ПУАССОН ТЕҢДЕУІ

Жалпы жағдайда Пуассон теңдеуі векторлық түрде былайша жазылады
[1,3]:

.
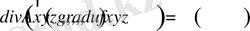(1.30)

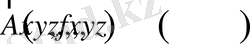Бұл жерде – белгісіз функция; – тәуелсіз айнымалылардың
функциялары.
Дербес туындылар арқылы (1.30) теңдеу былайша жазылады:

(1.31)

немесе, операторлық түрде:

.
(1.32)

Бұл жерде – Наббл операторы:

.
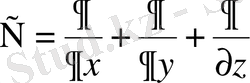(1.33)

Соңғы (1.30) - (1.32) өрнектерден Пуассон теңдеуі Лаплас теңдеуінің оң жағы
нолге тең болмаған кездегі түрі екенін көреміз. Осы айтылғанды жоғарыда
келтірілген есептерден көрсетейік.
Векторлық түрде (1.13) теңдеумен сипатталатын 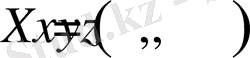үшөлшемді
кеңістіктің бетімен қоршалған көлеміндегі жылу таралуының
стационар есебін қарастырайық.
Егер көлемінде жылу көздері бар 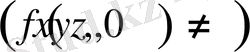және орта біртекті болмаса
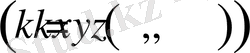, онда (1.13) дербес туындылы теңдеу былайша жазылады:

. (1.34)

немесе, операторлық түрде:

.
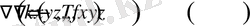(1.35)

Егер орта біртекті болса 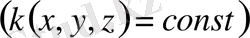, онда 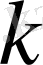шамасын (1.34) өрнекте
дербес туындының сыртына, ал (1.35) өрнекте Наббл операторының сыртына
шығарып жібереміз. Нәтижесінде Пуассон теңдеуінің жеке түрін аламыз:

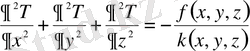(1.36)

немесе, операторлық түрде:

.
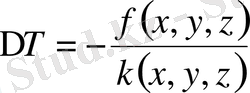(1.37)

Егер орта анизотропты болса, басқаша айтқанда, жылуөткізгіштік
коеффициенті 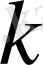жылудың таралу бағытына тәуелді

(1.38)

тензор болса, онда (1.34) теңдеу былайша түрленеді [1]:

.
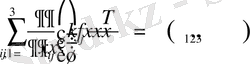(1.39)

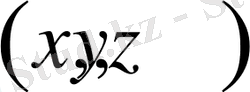Бұл жерде кеңістігі - ке сәйкес келеді.
Егер 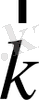тензорында бас диагональдың элементтерінен басқа
элементтер түгел нольге тең болса ( 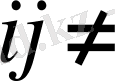үшін ), онда (1.39) теңдеу
былайша жазылады:

. (1.40)

Диффузия процестері диффундирленетін зат бар болса 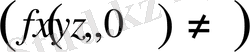және орта
біртекті емес болса 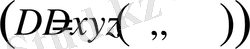векторлық түрдегі Пуассон теңдеуімен сипатталады:

.
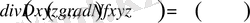(1.41)

Бұл теңдеу дербес туындылар арқылы:

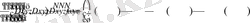(1.42)

немесе, операторлық түрде былайша жазылады:

.
(1.43)

Біртекті орта үшін 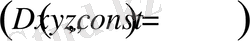(1.43) теңдеуін (1.36) сияқты былайша жазуға
болады:

(1.44)

немесе, операторлық түрде:

.
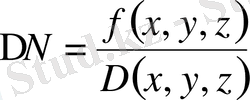(1.45)

Электр зарядтары бар кезде ток өткізбейтін ортада электр өрісінің
таралуы туралы есеп (1.23), (1.24) теңдеулерімен сипатталады. Векторлық
түрде (1.26) өрнекті ескере отырып былайша жазуға болады:

.
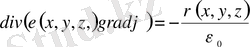(1.46)

Бұл теңдеуді дербес туындылар түрінде былайша

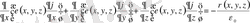(1.47)

немесе, операторлық түрде:

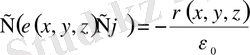(1.48)

жазуға болады.
Біртекті орта үшін (1.47) теңдеу былайша жазылады:

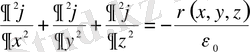(1.49)

немесе, операторлық түрде

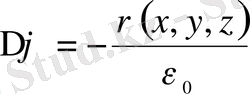(1.50)

түрінде жазылады.
Айта кету керек, жоғарыда қарастырылған, Лаплас немесе Пуассон
теңдеулерімен сипатталатын стационарлық жылуөткізгіштік процесі процесс
бейстационар болған кезде математикалық физика теңдеулерінің басқа класы,
параболалық теңдеумен сипатталады. Бұл теңдеу (1.35) теңдеудің
толықтырылған түрі және келесі түрлендірулер нәтижесінде (1.6) Фурье
заңынан алынады [2].
Үшөлшемді 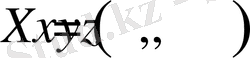кеңістіктің 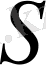бетімен қоршалған көлеміндегі
жылутаралудың бейстационар есебін қарастырайық.
Уақыттың аралығында 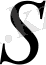бетімен қоршалған көлемінен
бөлініп шығатын жылу мөлшерін былайша есептеуге болады:

.
(1.51)

Бұл жерде уақыттың бір өлшемінде 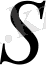бетімен қоршалған
көлемінен бөлініп шығатын жылудың (1.8) интегралмен есептелетін толық
мөлшері.
Жүйенің тепетеңдіксіз жағдайы қарастырылып отырғандықтан жылудың
келесі өрнекпен анықталатын бір 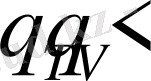бөлігі көлеміндегі
температураның уақыт бойынша өзгеруіне жұмсалады:

.
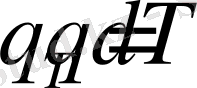(1.52)

Бұл жерде – көлеміндегі температураны бір градусқа өзгертуге
қажетті жылудың толық мөлшері; 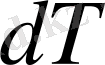– уақыттың аралығындағы
көлемінің температурасының өзгеруі.
Жылудың қалған 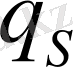бөлігі көлемді қоршап тұрған ауданы 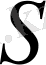беттен
ағып өтеді:

.
(1.53)

Бұл жерде уақыттың бір өлшемінде 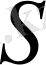беттен ағып өтетін жылудың
(1.7) – ші интегралмен анықталатын толық мөлшері.
Басқаша айтқанда, бейстационар жағдайда мынадай теңдеу орын алады:

.
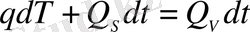(1.54)

Жалпы жағдайда біртекті емес орта үшін көлемінің температурасын
бір градусқа өзгертуге қажетті жылудың толық мөлшері келесі өрнекпен

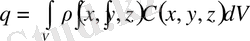(1.55)

анықталатынын ескерсек, онда (1.55), (1.7) және (1.8) өрнектерін (1.54)
теңдеуге қойып (1.10) Остроградский-Гаусс теоремасын қолдансақ мынадай
қатынас аламыз:

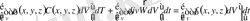. (1.56)

Бұл жерде 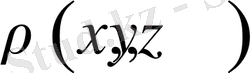– заттың тығыздығы; 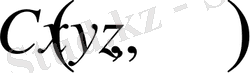– заттың меншікті жылу
сиымдылығы.
Соңғы теңдіктегі интеграл астындағы өрнектерді сыртқа шығарып
теңдіктің екі жағын да -ға бөлсек және нәтижесіне (1.6) Фурье заңын
қойсақ, онда жылуөткізгіштіктің бейстационар теңдеуін векторлық түрде жаза
аламыз:

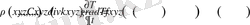. (1.57)

Бұл теңдеу операторлық түрде былайша жазылады:

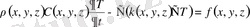. (1.58)

1.3 ШЕКАРАЛЫҚ ЖӘНЕ БАСТАПҚЫ ШАРТТАР

Жоғары математика курсынан әдетте дифференциалдық теңдеулердің жалпы
жағдайда шексіз көп шешімдері болатыны белгілі. Себебі, дифференциалдық
теңдеулерді интегралдау кезінде пайда болатын белгісіз тұрақты шамалардың
кез келген мәндері берілген дифференциалдық теңдеулерді қанағаттандырады
[6].
Математикалық физика есептерін шешу белгілі бір физикалық шамалардың
координаталар мен уақытқа тәуелділігін анықтаумен байланысты. Алынған шешім
әрқашан жалғызмәнді, шекті және үзіліссіз болу керек [6]. Басқаша айтқанда,
математикалық физиканың кез келген есебі жалғыз ғана шешімді (егер ол бар
болса) табуды талап етеді. Сондықтан физикалық есептің математикалық
қойылуы ізделіп отырған функцияны қарастырылып отырған аймақтың ішкі
нүктелерінде сипаттайтын негізгі теңдеулермен бірге (дербес туындылы
дифференциалдық теңдеулер) қосымша теңдеулерді де қамтуы керек. Қосымша
теңдеулер (дифференциалдық немесе алгебралық) белгісіз функцияның уақыттың
әрбір сәтіндегі шекаралық мәндерін және оның уақыттың алғашқы сәтіндегі
қарастырылып отырған аймақтың ішкі нүктелеріндегі мәндерін сипаттайды.
Аталған қосымша теңдеулер есептің шекаралық және бастапқы шарттары деп
аталады.

1.3.1 ШЕКАРАЛЫҚ ШАРТТАР

Кезкелген 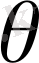аймағында математикалық физика теңдеуімен
сипатталатын белгілі бір есепті шешу қажет болсын делік. Есептің жалғыз
ғана шешімін табу үшін шекаралық шарт белгілі болу керек, басқаша айтқанда,
белгісіз айнымалылардың 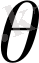аймағының шекаралық бөлігіндегі
мәндерін нақты теңдеулермен беру керек.
Егер 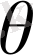аймағы үшөлшемді кеңістіктегі кезкелген көлем болса, онда
берілген көлемді қоршап тұрған тұйық бет болады. Егер 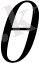аймағы
екіөлшемді кеңістіктегі кезкелген бет болса, онда берілген бетті
қоршап тұрған тұйық контур болады. Ең соңында, егер 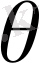аймағы бірөлшемді
кеңістіктегі кезкелген кесінді болса, онда берілген кесіндінің екі
шеткі нүктесі болады.
Шекаралық шарттарды беретін теңдеулердің түріне қарап оларды бірінші
текті (Дирихле шарттары), екінші текті (Нейман шарттары) және үшінші текті
деп бөледі [2].
Бірінші текті шекаралық шарттар немесе Дирихленің шекаралық есебі
былайша беріледі:

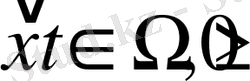болғанда .
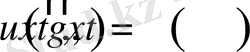(1.59)

Бұл жерде 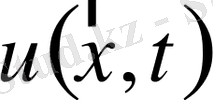- ізделіп отырған белгісіз функция; -
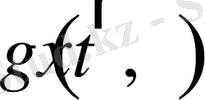шекарасында берілген кезкелген функция; 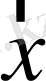- шекаралық нүктенің
кеңістіктегі координаталары (мысалы, үшөлшемді кеңістік үшін );
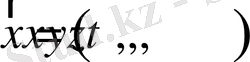- уақыт.
Егер жылуөткізгіштік есебі қарастырылып отырса, онда бірінші текті
шекаралық шарт шекарасындағы температураны береді. Ток өткізбейтін
ортадағы элетростатикалық өрістің таралуы есебінде бірінші текті шекаралық
шарт шекарасындағы электр потенциалын береді және т.б.
Екінші текті шекаралық шарттар немесе Нейманның шекаралық есебі
былайша беріледі:

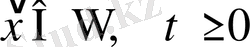болғанда .
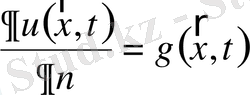(1.60)

Бұл жерде - шекарасының ішкі нормалі.
Басқаша айтқанда, Нейман шарттары шекарадағы ағынды, дәлірек айтсақ,
ағын векторының шекараға түсетін нормальға проекциясын береді. Мысалы,
жылуөткізгіштік есептерінде екінші текті шекаралық шарттар жылу ағынын
береді, ал ток өткізбейтін ортада электростатикалық өрістің таралуы туралы
есепте – электр өрісінің кернеулігінің векторының шекараға түсетін
нормальға проекциясын береді және т.б.
Үшінші текті шекаралық шарттар Дирихле мен Нейман есептерінің
жалпыланған түріне жатады және былайша жазылады:

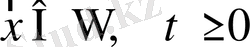болғанда 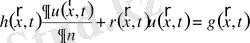. (1.61)

Бұл жерде - координаталар мен уақыттың белгілі функциялары. Мысалы,
жылу есептерінде үшінші текті шекаралық шарттар шекарадағы конвективті жылу
алмасу мен сәулелік жылу алмасуды беруге пайдаланылады.
Ньютон заңына сәйкес, қатты дененің бетінен уақыттың бір өлшемінде
газды немесе сұйық ортаға берілетін немесе олардан алынатын жылу ағынынының
тығыздығы былайша анықталады:

.
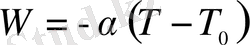(1.62)

Бұл жерде - конвективті жылу алмасу коэффициенті; - қатты
дененің бетінің температурасы; 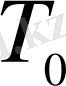- қоршаған ортаның температурасы [6].
Шекараға нормальдың бойындағы жылу ағынының тығыздығына (1.6) Фурье
заңын қолдансақ және (1.62) және (1.6) теңдеулерінің оң жақтарын өзара
теңестірсек үшінші текті шекаралық шарттарды аламыз:

;
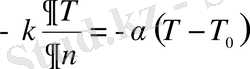(1.63)
.
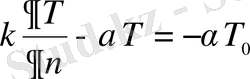(1.64)

Больцман заңына сәйкес, қатты дененің бетінен уақыттың бір өлшемінде
сәуле шашу арқылы бөлінетін жылу ағынынының тығыздығы былайша анықталады:

.
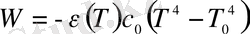(1.65)

Бұл жерде – абсолют қара дененің сәуле шашу коэффициенті; –
салыстырмалы сәуле шашу қабілеті немесе дененің қаралық дәрежесі [6].
Шекараға нормальдың бойындағы жылу ағынынының тығыздығына (1.6) Фурье
заңын қолдансақ және (1.65), (1.6) теңдеулерінің оң жақтарын өзара
теңестірсек үшінші текті шекаралық шарттарды аламыз:

;
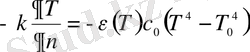(1.66)
.
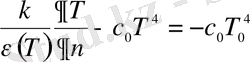(1.67)

(1.62)-(1.67) теңдеулерде температура дененің бетіндегі
нүктелердің координаталарының 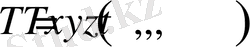функциясы.
Ескерте кету керек, әрбір айнымалы үшін шекаралық шарттардың саны
дифференциалдық теңдеулердегі туындылардың ретімен анықталады [5]: бірінші
ретті теңдеулер үшін – бір шекаралық шарт, екінші ретті теңдеулер үшін –
екі, үшінші ретті теңдеу үшін – үш шекаралық шарт және т.б.

1.3.2 БАСТАПҚЫ ШАРТТАР

Бейстационар, уақыт бойынша өзгеріп отыратын физикалық процестерді
сипаттайтын есептердің жалғыз ғана шешімін табу үшін шекаралық шарттармен
бірге бастапқы шарттарды да беру керек. Бастапқы шарттар айнымалылардың
немесе олардың градиенттерінің қарастырылып отырған 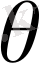аймағының
шекаралық нүктелерінен бөлек ішкі нүктелеріндегі уақыттың бастапқы
сәтіндегі мәндерін қамтиды :

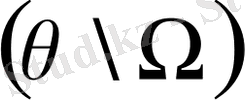болғанда ;

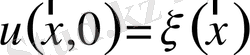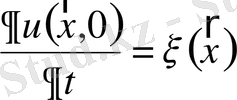болғанда ;

болғанда .

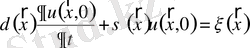Бұл жерде 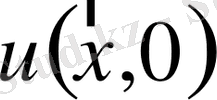– ізделіп отырған белгісіз функцияның уақыттың бастапқы
сәтіндегі мәні; – координаталардың белгілі функциялары.
Шекаралық шарттар сияқты, бастапқы шарттардың саны да дифференциалдық
теңдеулердегі уақыт бойынша туындылардың ең үлкен ретімен анықталады [5].

2 ЭЛЛИПСТІК ТЕҢДЕУЛЕРДІҢ ЕСЕПТЕРІН ШЕКТІ
АЙЫРЫМДАР ӘДІСІМЕН ШЕШУ

2.1 ПУАССОННЫҢ БІРӨЛШЕМДІ ТЕҢДЕУІН ШЕКТІ
АЙЫРЫМДАР ӘДІСІМЕН ШЕШУ

Пуассонның бірөлшемді

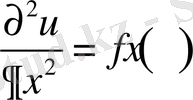(2.1)

түріндегі теңдеуін қарастырайық [2]. Бұл жерде 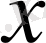– координата; –
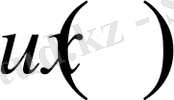ізделіп отырған функция; 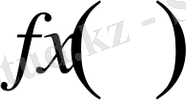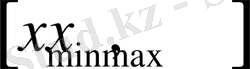– кесіндісінің 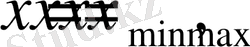нүктелерінде
Дирихле немесе Нейманның шекаралық шарттары берілген үзіліссіз функция.
Енді 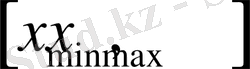кесіндісінде қадамы 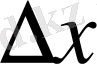біркелкі координаталық торды
берейік:

.
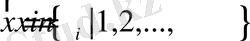(2.2)

Қарастырылып отырған есеп үшін бірінші текті шекаралық шарттарды
(Дирихле) мынадай түрде беруге болады:

;
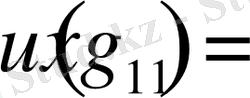(2.3)
.
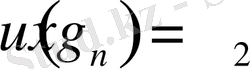(2.4)

Бұл жерде 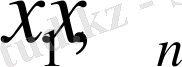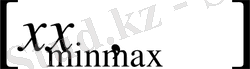– аймағының шекаралық нүктелерінің координаталары;
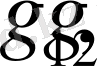- кез келген тұрақты шамалар.
Қарастырылып отырған есеп үшін екінші текті шекаралық шарттарды
(Нейман) мынадай түрде беруге болады:

;
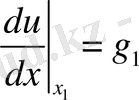(2.5)
.
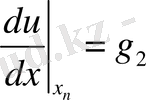(2.6)

Шекаралық шарттарды (2.2) координаталық торда шекті айырымдар әдісі
бойынша дискреттесек:

;
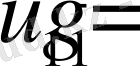(2.7)

(2.8)

мәндерін аламыз. Бұл жерде 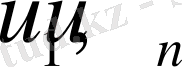шамалары 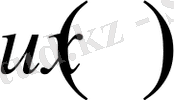функциясының
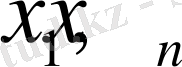нүктелеріндегі мәндері.
Сол сияқты Нейманның шекаралық шарттарын (2.2) торында дискреттеп

;
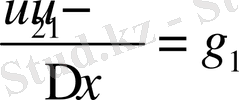(2.9)
;
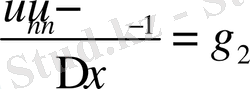(2.10)

мәндерін аламыз.
Енді (2.1) теңдеуін тордың ішкі нүктелерінде дискреттесек

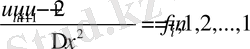(2.11)

теңдеулер жүйесін аламыз. Бұл жерде шамасы функциясының тордың
координатасы нүктесіндегі мәні.
Осылайша, дискреттеу нәтижесінде, өлшемі болатын сызықтық
теңдеулер жүйесін алдық. Жүйенің құрамында ішкі нүктелерге қатысты (2.11)
түріндегі теңдеу, және екі шекаралық нүктеге қатысты (2.7), (2.8),
немесе (2.9), (2.10) теңдеулер бар.

2. ПУАССОННЫҢ ЕКІӨЛШЕМДІ ТЕҢДЕУІН ШЕКТІ
АЙЫРЫМДАР ӘДІСІМЕН ШЕШУ

Пуассонның екіөлшемді

(2.12)

түріндегі теңдеуін қарастырайық [2]. Бұл жерде – координаталар;
– ізделіп отырған функция; – төртбұрышты аймақтың
шекаралық нүктелерінде Дирихле немесе Нейманның шекаралық шарттары берілген
үзіліссіз функция.
Енді кесіндісінде қадамы біркелкі координаталық торды
берейік:

,
(2.13)

ал кесіндісінде қадамы біркелкі координаталық торды берейік:

.
(2.14)

Жоғарыдағы (2.13) және (2.13) векторлары тікбұрышты аймақта екіөлшемді

(2.15)

біркелкі торды анықтайды
Қарастырылып отырған есеп үшін бірінші текті шекаралық шарттарды
(Дирихле) мынадай түрде беруге болады:

;
(2.16)
;
(2.17)
;
(2.18)
;
(2.19)

Бұл жерде – аймағының шекаралық нүктелерінің координаталары;
– аймағының шекаралық нүктелерінің координаталары; –
сәйкес координаталардың кез келген үзіліссіз функциялары.
Қарастырылып отырған есеп үшін екінші текті шекаралық шарттарды
(Нейман) мынадай түрде беруге болады:

;
(2.20)
;
(2.21)
;
(2.22)
;
(2.23)

Шекаралық шарттарды (2.15) координаталық торда шекті айырымдар әдісі
бойынша дискреттесек:

;
(2.24)
;
(2.25)
;
(2.26)

(2.27)

мәндерін аламыз. Бұл жерде шамалары функциясының
нүктелеріндегі мәндері.
Сол сияқты Нейманның шекаралық шарттарын (2.15) торында дискреттеп

;
(2.28)
;
(2.29)
;
(2.30)

(2.31)

мәндерін аламыз.
Енді (2.12) теңдеуін тордың ішкі нүктелерінде дискреттесек

(2.32)

теңдеулер жүйесін аламыз. Бұл жерде мәндері функциясының
тордағы координаталы нүктелердегі мәндері.
Осылайша, дискреттеу нәтижесінде, өлшемі болатын сызықтық
алгебралық теңдеулер жүйесін алдық. Жүйенің құрамында ішкі нүктелерге
қатысты (2.32) түріндегі теңдеулер және шекаралық нүктелерге қатысты
(2.24) немесе (2.28), (2.25) немесе (2.29), (2.26) немесе (2.30), (2.27)
немесе (2.31) түріндегі теңдеулер бар.
Төменде шекаралық шарттары (2.16) - (2.23) өрнектері арқылы берілген
(2.12) теңдеуді (2.15) торда шекті айырымдар әдісімен MATLAB программалау
жүйесінде шешудің бір нұсқасы келтірілген.

% Екі өлшемді d2udx2+ d2udy2=f(x,y) Пуассон теңдеуін тікбұрышты
% аймақта Дирихле жәненемесе Нейман шарттарымен бірге шекті айырымдар %
әдісімен шешу

function[x,y,U]=...
puass_2d(x0,xn,n,y0,ym,m,f,v1,g1,v2 ,g2,v3,g3,v4,g4)
% puass_2d функциясына енгізілетін компоненттердің мағыналары:
% xo-есептеу аймағының х өсі бойындағы бастапқы координатасы;
% xn- есептеу аймағының х өсі бойындағы соңғы координатасы;
% y0- есептеу аймағының у өсі бойындағы бастапқы координатасы;
% ym- есептеу аймағының у өсі бойындағы соңғы координатасы;
% n-координалық тордың х өсі бойындағы нүктелер саны;
% m-координалық тордың у өсі бойындағы нүктелер саны;
% f-Пуассон теңдеуінің оң жақ функциясы. Екі тырнақшаның арасында
% орналасқан символдар жинағы түрінде беріледі. Мысалы:‘exp(-x)+exp(-y)’
% v1-аймақтың бірінші x=x(1) шекарасындағы шекаралық шарттың түрін
% білдіретін параметр(1- Дирихле шарта, 2-Нейман шарты).
% g1-аймақтың бірінші шекарасында шекаралық шарттың оң жағында
% берілетін функция. Екі тырнақшаның арасында орналасқан символдар
% жинағы түрінде беріледі.
% v2-аймақтың екінші x=x(n) шекарасындағы шекаралық шарттың түрін
% білдіретін параметр(1- Дирихле шарта, 2-Нейман шарты).
% g2-аймақтың екінші шекарасында шекаралық шарттың оң жағында
% берілетін функция. Екі тырнақшаның арасында орналасқан символдар
% жинағы түрінде беріледі.
% v3-аймақтың үшінші y=y(1) шекарасындағы шекаралық шарттың түрін %
білдіретін параметр(1- Дирихле шарта, 2-Нейман шарты).
% g3-аймақтың үшінші шекарасында шекаралық шарттың оң жағында
% берілетін функция. Екі тырнақшаның арасында орналасқан символдар
% жинағы түрінде беріледі.
% v4-аймақтың төртінші y=y(n) шекарасындағы шекаралық шарттың түрін %
білдіретін параметр(1- Дирихле шарта, 2-Нейман шарты).
% g4-аймақтың төртінші шекарасында шекаралық шарттың оң жағында
% берілетін функция. Екі тырнақшаның арасында орналасқан символдар
% жинағы түрінде беріледі.

% puass_2d функциясынан алынатын компоненттердің мағыналары:
% x-х өсі бойындағы өлшемі 1*n болатын вектор-қатар;
% y- y өсі бойындағы өлшемі 1*m болатын вектор-қатар;
% U-ізделіп отырған U функциясының координаталық тордың түйіндерінде
% анықталған мәндерінен тұратын өлшемі n*m болатын матрица.

% Бастапқы және шекаралық шарттар

x0=0; xn=1; n=10;
y0=0; ym=2; m=20;
f=’exp(-x)+exp(-y);
v1=1; g1=’sin(y^2)’;
v2=1; g2=’cos(3*y)’;
v3=2; g3=’10*sin(x^2)’;
v4=2; g4=’10*sin(6*x)’;

% Біркелкі координаталар торын беру

x=x0:(xn-xo)(n-1):xn; dx=x(2)-x(1);
y=y0:(ym-yo)(m-1):ym; dy=y(2)-y(1);

% Символдар түрінде берілген функциялардың координаталар торының
% түйіндеріндегі мәндерін есептеу

F=inline(f,’x’,’y’);
G1=inline(g1,’y’);
G2=inline(g2,’y’);
G3=inline(g3,’x’);
G4=inline(g4,’x’);

% Сызықтық алгебралық теңдеулер жүйесінің (СЛАУ) ретін анықтау

N=n*m;

% СЛАУ-дың өлшемі n*n болатын толық матрицасын тазалау (нөлдермен %
толтыру)

a=zeros(N,N);

% СЛАУ-дың өлшемі 1*n болатын оң жақ бос мүшелері векторын тазалау %
(нөлдермен толтыру)

b= zeros(1,N);

% СЛАУ-дың коэффициенттері мен шекаралық шарттарға сәйкес бос
% мүшелерін анықтау және v1, v2, v3, v4 параметрлерінің мәндерінің
% дұрыстығын тексеру

for j=1:m
b(j)=G1(y(j));
if v1==1
a(j,j)=1;
elseif v1==2
a(j,j)=-1dx;
a(j,m+j)=1dx;
else
error(‘Parameter v1 have incorrect value’);
end
b(m*(n-1)+j)=G2(y(j));
if v2==1
a(m*(n-1)+j, m*(n-1)+j)=1;
elseif v2==2
a(m*(n-1)+j, m*(n-1)+j)=1dx;
a(m*(n-1)+j, m*(n-2)+j)=-1dx;
else
error(‘Parameter v2 have incorrect value’);
end
end
for i=2:n-1
b(m*(i-1)+1)=G3(x(i));
if v3==1
a(m*(i-1)+1, m*(i-1)+1)=1;
elseif v3==2
a(m*(i-1)+1, m*(i-1)+1)=-1dy;
a(m*(i-1)+1, m*(i-1)+2)=1dy;
else
error(‘Parameter v3 have incorrect value’);
end
b(m*(i-1)+m)=G4(x(i));
if v4==1
a(m*(i-1)+m, m*(i-1)+m)=1;
elseif v4==2
a(m*(i-1)+m, m*(i-1)+m)=1dy;
a(m*(i-1)+m, m*(i-1)+m-1)=-1dy;
else
error(‘Parameter v4 have incorrect value’);
end
end

% СЛАУ-дың коэффициенттері мен ішкі нүктелерге сәйкес бос

% мүшелерін анықтау

for i=2:n-1
for j=2:m-1
a(m*(i-1)+j, m*(i-1)+j)=-2dx^2-2dy^2;
a(m*(i-1)+j, m*(i)+j)=1dx^2;
a(m*(i-1)+j, m*(i-2)+j)=1dx^2;
a(m*(i-1)+j, m*(i-1)+j+1)=1dy^2;
a(m*(i-1)+j, m*(i-1)+j-1)=1dy^2;
b(m*(i-1)+j)=F(x(i),y(j));
end
end

% СЛАУ-ды шешу

u=b\a’;
% Ізделіп отырған функцияның координаталық тордың түйіндеріндеріндегі %
мәндерінің вектор-қатарын график түрінде көрсетуге ыңғайлы түрге
% келтіру

for i=1:n
for j=1:m
U(i,j)=u(m*(i-1)+j);
end
end

% Ізделіп отырған U(x,y) функциясының графигін тұрғызу

surf(y,x,U)
xlabel(‘y’)
ylabel(‘x’)
zlabel(‘U’)
grid on

Жоғарыда келтірілген есептеу программасын puass_2d.m деген атпен
текстік файл түрінде MATLAB жүйесінің [10-12] түбіртек каталогында
орналасқан \WORK каталогында сақтау керек.
Келесі командалар арқылы puass_2d.m функциясын шақыруға болады:

puass_2d;
x= puass_2d;
[x,y]= puass_2d;
[x,y,U]= puass_2d;
[x,y,U]= puass_2d(x0,xn,n,y0,ym,m,f,v1,g1,v2 ,g2,v3,g3,v4,g4).

Бірінші, екінші, үшінші немесе төртінші командаларды орындағанда
функция графиктік шешімдерді алдын ала тағайындалмаған, MATLAB-тың
шешімімен автоматтаты түрде тағайындалған параметрлер үшін береді [2].
Функцияны бірінші немесе екінші командалар арқылы, команданың
текстінен кейін ; символын қолданбанбай шақырған жағдайда монитордың
экранында графикалық суретпен бірге х бойынша түйіндердің координаталарының
векторы шығады. Керісінше, ; символын қолданған кезде бұл вектор
шығарылмайды.
Функцияны үшінші команда арқылы ; символын қолданбанбай шақырған
жағдайда монитордың экранында графикалық суретпен бірге х бойынша
түйіндердің координаталарының векторы және у бойынша түйіндердің
координаталарының векторы шығады.
Егер үшінші немесе төртінші командалар ; символын қолданбанбай
шақырылса, монитор экранында шешімнің графигі, тордағы түйіндердің х
координаталарының векторы, тордағы түйіндердің у координаталарының векторы
және тордың түйіндеріндегі U функциясының мәндерінің векторы шығады.

Сурет 2.1

Мысалы, функцияны

puass_2d;

командасы арқылы шақырғанда функциясының мәні 200 нүктесі бар
аралықтың нүктелерінде келесі

шекаралық шарттар арқылы анықталса, онда экранда есептің шешімінің
үшөлшемді графигі (2.1 сурет) мониторда шығады.

3 ЭЛЛИПС ТЕКТЕС ТЕҢДЕУЛЕРДІ ШЕКТІ ЭЛЕМЕНТТЕР
ӘДІСІМЕН ШЕШУ

3.1 ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІНІҢ НЕГІЗГІ КОНЦЕПЦИЯСЫ

Шекті элементтер әдісі жаратылыстану ғылымдарында зерттелетін
процестерді сипаттайтын дифференциалдық теңдеулерді сандық әдіспен шешуге
арналған. Космостық зерттеулерден туған есептерді шешуге байланысты пайда
болған (1950 ж) әдіс, алғаш рет Тернердің, Клуждың, Мартин мен Топптың
еңбектерінде жарық көрді [6]. Осыдан кейін әдіс құрылыс механикасында,
тұтас денелердің кернеулі-деформациялық күйін зерттеу есептерінде,
қолданыла бастады. Әдісті теориялық жағынан негіздеген Мелош болды. Ол
шекті элементтер әдісінің осыған дейін кеңінен таралған Рэлей-Ритц әдісінің
бір варианты екенін дәлелдеді. Шекті элементтер әдісінде тұтас дененің
кернеулі-деформациялық күйін анықтау есебі деформацияның толық потенциалдық
энергиясын минималдау арқылы сызықтық алгебралық теңдеулер жүйесін шешу
есебіне келтіріледі.
Шекті элементтер әдісінің минималдау процедурасымен байланысы әдісті
техниканың басқа салаларындағы көптеген есептерді шешуге кеңінен
пайдалануға мүмкіндік берді. Әдіс, Лаплас немесе Пуассон теңдеулерімен
сипатталатын есептерді шешуге кеңінен қолданылды. Алғашқы зерттеулерде
шекті элементтер әдісі жылу таралу есептерін шешуге қолданылды. Кейіннен,
әдіс гидромеханиканың есептеріне, атап айтқанда, қуысты ортада сұйықтардың
ағу процестерін зерттеуге қолданыла бастады.
Шекті элементтер әдісін қолдану саласының кеңуіне құрылыс
механикасында, жылу таралу процестерінде, гидромеханикада қолданылатын
теңдеулер Галеркин әдісімен, немесе, ең кіші квадраттар тәсілімен оңай
алынатынының дәлелденуі көп ықпал етті. Бұл фактор әдісті теориялық жағынан
негіздеуге көмектесіп, оны кез келген дифференциалдық теңдеулерді шешуде
қолдануға мүмкіндік берді.
Шекті элементтер әдісі құрылыс механикасы есептерін шешуге арналған
әдістен барлық дифференциалдық теңдеулерді шешуге арналған жалпы әдіске
айналды. Бұл прогреске есептеу машиналарының күрт дамуына, ұшу аппараттарын
дәлірек зерттеу қажеттігіне, космостық зерттеулердің кеңінен дамуына
байланысты қол жетті. Қазіргі кезде, шекті элементтер әдісі автомобильдер,
самолеттер, ракеталар жасау салаларында, атом реакторларын жобалауда
кеңінен қолданылады.
Шекті элементтер әдісі тұтас денедегі скалярлық немесе векторлық
шамаларды сипаттайтын үзіліссіз функцияны тұтас денені құрайтын шекті
аймақтарда анықталатын бөлшекті-үзіліссіз функциялар жинағымен алмастыруға
негізделген.
Бұл кезде бөлшекті-үзіліссіз функция берілген үзіліссіз функцияның
зерттеу аймағының нақты нүктелеріндегі мәндері арқылы анықталады [6].
Алдымен тұтас аймақты кіші аймақтарға ойша жіктеу нәтижесінде пайда
болатын нүктелер тағайындалады. Бұл нүктелерді түйіндік нүктелер немесе
түйіндер деп атайды. Жалпы жағдайда белгісіз үзіліссіз функция енді осы
түйіндерде анықталады. Дискретті моделді құру үшін алғашында үзіліссіз
шаманың сандық мәндері шартты түрде аймақтың түйіндерінде анықталған деп
алынады. Одан кейін жалпы жағдайға көшуге болады. Сонымен, үзіліссіз
шаманың дискретті моделін құру мынадай ретпен орындалады:
- қарастырылып отырған аймақта жалпы саны шектелген нүктелер белгіленеді.
Бұл нүктелерді түйіндік нүктелер немесе түйіндер деп атайды;
- үзіліссіз шаманың әрбір түйіндегі мәні айнымалы және оларды анықтау
керек;
- үзіліссіз шаманың анықталу аймағы жалпы саны шектелген кіші аймақтарға
бөлшектеледі. Бұл кіші аймақтарды элементтер деп атайды. Көрші тұрған
элементтердің ортақ түйіндері болады және элементтердің толық жиыны
берілген аймақты жуықтап аппроксимациялайды;
- үзіліссіз шама әрбір элемент ішінде полином арқылы аппроксимацияланады.
Полиномның коэффициенттері үзіліссіз шаманың түйіндердегі шартты түрде
белгілі деп алынған мәндері арқылы анықталады.

Сурет 3.1
Сурет 3.2

Шекті элементтер әдісінің негізгі концепциясын келесі мысал арқылы
көрнекі түсіндіруге болады. Анықталу аймағы осінің бойынан алынған
кесіндісі болатын үзіліссіз шамасы қарастырылсын (3.1 сурет).
Суретте осінің бойында бес нүкте белгіленіп, номерленген. Бұл
түйіндік нүктелерді өзара бірдей қашықтықта орналастыру шарт емес. Нүктелер
санын көбейтуге болады, бірақ әдістің негізгі идеясын түсіндіруге осы бес
нүктенің өзі жеткілікті. Үзіліссіз шамасының әрбір түйіндегі мәні
белгілі деп есептелінсін. Бұл мәндер 3.2 б суретте көрсетілген және
түйіндердің номерлеріне сәйкес деп белгіленген.
Аймақты элементтерге бөлудің екі түрлі тәсілі бар. Мысалы, әрбір
элементті екі түйінмен шектеуге болады (3.3а сурет). Бұл кезде кесінді төрт
элементке бөлінеді. Немесе, егер кесінді екі элементке бөлінсе, онда әрбір
элементте үш түйін тағайындалады (3.3б сурет). Әрбір элементке сәйкес
аппокцимациялау полиномының коэффициенттері функциясының элементтің
түйіндеріндегі мәндері арқылы анықталады. Аймақты төрт элементке бөлген
жағдайда әрбір элементте екі түйін болады да, элементтің функциясы
айнымалысына қатысты сызықтық функция болады (кезкелген түзу екі нүкте
арқылы анықталатын болғандықтан). функциясының толық аппроксимациясы
әрқайсысы жеке элементте анықталған төрт бөлшекті-сызықтық функциялардан
тұрады (3.4а сурет).

а
б
Сурет 3.3

а
б
Сурет 3.4

Аймақты бөлудің екінші тәсілінде кесіндіде әрқайсысының үш түйіні бар
екі элемент тағайындалады да, әрбір элементтің функциясы (полиномы) екінші
дәрежелі полиноммен беріледі. Бұл кезде функциясының толық
аппроксимациясы әрқайсысы жеке элементте анықталған екі бөлшекті- үзіліссіз
квадраттық функциялардың жинағынан тұрады (3.4б сурет).
Бұл жуықтау бөлшекті-үзіліссіз жуықтау болатыны даусыз, себебі
элементтердің шекараларындағы түйінде бұл функциялардың осы түйіндегі
жанамаларының бұрыштық коэффициенттері әртүрлі болуы мүмкін.
Жалпы жағдайда, температураның таралу заңдылығы белгісіз
болғандықтан, температураның тағайындалған түйіндердегі мәндерін анықтау
қажет. Дискретті моделді құру әдісі бұрынғыша сақталады, тек бұл жолы
қосымша қадам пайда болады. Тағы да түйіндер жиыны анықталады және осы
түйіндердегі температураның мәндері бұл жолы айнымалы деп алынып,
оларды анықтау қажеттілігі туады. Зерттеу аймағы әрқайсысында элементтің
сәйкес функциясы (полиномы) анықталған элементтерге бөлінеді.

Сурет 3.5

Енді функциясының түйіндік мәндерін температураның шын мәндеріне
мейлінше жақындату үшін есептің физикалық мағынасымен байланысқан белгілі
бір шаманы минималдау қажет. Егер жылу таралу есебі қарастырылып отырса,
онда сәйкес дифференциалдық теңдеумен байланысты функционал минималданады.
Функционал ретінде тұтас денеде жинақталатын жылудың толық мөлшерін
есептеу интегралы алынады. Функционалды минималдау процесі
функциясының түйіндік мәндеріне қатысты құрылған сызықтық алгебралық
теңдеулер жүйесін шешуге алып келеді.
Екі- немесе үшөлшемді аймақта анықталған үзіліссіз шаманың дискретті
моделін құрған кезде де шекті элементтер әдісінің негізгі концепциясы
сақталады. Екі өлшемді жағдайда элементтер айнымалыларына тәуелді
функциямен сипатталады. Бұл кезде көбінесе үшбұрыш немесе төртбұрыш
түріндегі элементтер қолданылады.
Элементтердің функциялары жазық (3.5 сурет) немесе қисық (3.6 сурет)
беттермен көрсетіледі. Егер элемент үшін түйіндік нүктелердің ең аз саны
пайдаланылса, онда элементтің функциясы жазық бетпен көрсетіледі. Демек,
үшбұрышты элемент үшін үш түйін, ал төрт бұрышты элемент үшін төрт түйін
алынады (3.5 сурет).
Егер қолданылатын түйіндер саны минималдық шамадан артық болса, онда
элементтің функциясына қисық бет сәйкес келеді. Оның үстіне элементтердің
артық саны шекарасы қисық сызықты элементті қарастыруға мүмкіндік береді.
Екі өлшемді үзіліссіз шаманың толық аппроксимациясы бөлшекті-
үзіліссіз беттердің жиыны түрінде беріледі. Бұл беттердің әрқайсысы
функциясының сәйкес элементтің түйіндеріндегі мәндері арқылы анықталады.

Сурет 3.6

Шекті элементтер әдісінің маңызды аспекті оның элементтер жинағы
ішінен кез келген элементті бөліп алып қарастыру мүмкіндігінде. Бұл аспект
әрбір элементтің тек өзіне тән қасиеттерін ескеруге мүмкіндік береді, ал
пайдаланылатын түйіндер санын еркін таңдау мүмкіндігі қарастырылып отырған
аймақтың күрделі геометриясын ескеруді жеңілдетеді. Ескерте кететін жағдай,
3.5 және 3.6 суреттерде келтірілген кеңістік беттер функциясының
кеңістігіндегі ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.