Алгебра элементтерін дамыта оқыту (4-сынып)

Пән: Педагогика
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 80 бет
Таңдаулыға:

Ф-ОБ-001/033

Қазақстан Республикасы Білім және ғылым министірлігі

Қожа Ахмет Ясауи атындағы Халықаралық қазақ-түрік университеті

«Қорғауға жіберілді»

«Бастауыш оқыту теориясы мен

әдістемесі» кафедрасының

меңгерушісі, п. ғ. к., доц. м. а.

Тоққұлова Г. Т.

«» 2014 ж.

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: Алгебра элементтерін дамыта оқыту (4-сынып)

5В010200 - «Бастауыш оқыту педагогикасы мен әдістемесі» мамандығы

Орындаған Батырбекова А.

Ғылыми жетекшісі,

аға оқытушы Даулетбекова Б.

Түркістан-2014

Мазмұны

Нормативтік сілтемелер4

Анықтамалар4

Белгілеулер мен қысқартулар 5

Аннотация5

Кіріспе6

І. БАСТАУЫШ МАТЕМАТИКА КУРСЫН ДАМЫТА ОҚЫТУ ТЕХНОЛОГИЯСЫН ҚОЛДАНУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

Бастауыш математика мазмұнына жалпы сипаттама8
Бастауыш математика курсындағы алгебра элементтеріне жалпы түсініктеме-18
Дамыта оқыту технологиясының маңыздылығы22

ІІ. АЛГЕБРА ЭЛЕМЕНТТЕРІН ДАМЫТА ОҚЫТУ ӘДІСТЕМЕСІ

(4-СЫНЫП)

Сандық өрнектер құруға үйретуде оқу есептерінің маңызы30
Дамыта оқыту технологиясын алгебра элементтерін оқытуда қолдану---46
Есептерді шешуде алгебралық әдісті пайдаланудың тиімділігі52

Қорытынды66

Пайдаланылған әдебиеттер68

Қосымша70

Нормативтік сілтемелер

Осы дипломдық жұмыста келесі нормативтік құжаттарға сілтеме жасалған:

-Қазақстан Республикасы 2007-жылғы 27-шілдедегі «Білім туралы» заңы;

-Оқу бағдарламасы Қазақстан Республикасы Үкіметінің 2012-жылғы 23-тамыздағы №1080 қаулысымен бекітілген Орта білім берудің (бастауыш, негізгі орта, жалпы орта білім беру) мемлекеттік жалпыға міндетті стандарты.

-Университетінің ішкі нормативтік ережесі:

УЕ-ХҚТУ-015-2014 Дипломдық жұмысты (жобаны) әзірлеу мен рәсімдеуге қойылатын жалпы талаптар;

Анықтамалар

1) Есептер- жаттығулар, олардың көмегімен ең алдымен математиканың бастауыш курсының көптеген мәселелері айқындалады.

2) Дамыта оқыту - оқушылардың танымдық сұранысының нысанивті көрінісі ретінде, яғни олардың шығармашылық есептерді орындауда білімі, біліктілік және машақтарға ие болуларына бағытталған қауырт оқу танымдық іс-әрекеті ретінде көрінеді.

3) Оқу - адамның психикалық дамуының формасы, элементі. Кез келген оқыту белгілі бір мөлшерде адамды дамытады.

4) «Даму» ұғымы сөздікте « . . . мөлшерлік өзгерістердің белгілі бір өлшем шегінен шығып, сапалық өзгерістерге айналуы, »-деп түсіндіріледі.

5) «Даму» ұғымының психологиялық анықтамасы-жаңарту процесі, жаңаның өмірге келіп, ескінің жоғалуы деген мағынаны береді. Барлық табиғат құбылыстары сияқты бала психикасы да үнемі диалектикалық жолмен дамып, өзгеріп, бір деңгейден екінші деңгейге өтіп отырады.

6) Бала дамуының жақын аймағы - баланың тек үлкендердің көмегі арқылы атқара алатын істері. Ал бала дамуының қол жеткен аймағы - баланың үлкендердің көмегінсіз істей алатын істері.

7) Тендеу құру дегеніміз- есептің мазмұнын математика тіліне аудару.

8) Арифметикалық, алгебралық және геометриялық материалды оқып үйренумен тығыз байланыстырыла отырып шама ұғымымен шамаларды өлшеу идеясы айқындалады.

9) Арифметикалық амалдарға қатысты аталған барлық мәселелер бір-бірімен өзара тығыз байланыста қарастырылады.

10) Теңдеулер құру арқылы есептер екі кезең қарастырылады: олардың біреуінде теңдеулер құру арқылы есептер шығаруға дайындық жұмысы жүргізіледі, ал екіншісінде есептердің шарттары бойынша теңдеулер құрудың әр түрлі әдістері қарастырылады, оны игеру оқушыларды теңдеулер құру арқылы программада қарастырылған есептерді шығара білуге әкеп тірейді.

Белгілеулер мен қысқартулар

Университет- Қ. А. Ясауи атындағы қазақ-түрік универтситеті;

БМ- Бастауыш мектеп;

ҚР- Қазақстан Республикасы;

БС-Бастауыш сынып.

Аннотация

Развивающее обучение алгебраических элементов.

Developіng learnіng algebraic elements.

Cebirsel öğe öğrenme geliştirme.

КІРІСПЕ

Зерттеу жұмысының көкейтестілігі: Қазіргі заманның талаптарына сай еңбекке, қоршаған ортаға, қоғамға деген қарым - қатынастылықтар мен көзқарастарды қалыптастыру мектеп курсының барлық пәндерін оқыту үдерісінде жүргізіледі, орындалады. Алайда, осы бағытта математика пәнін алып қарастыратын болсақ, оның оқытудағы әдіс - тәсілді ерекшеліктеріне байланысты тәрбиелеуде өте қуатты құрал болып табылатыны сөзсіз.

Оқытудың жаңа технологияларын білім беру бағдарламаларының қоғам мен еңбек нарығының өзгеріп отыратын қажеттеріне тез бейімделуіне ықпал ететін кредиттік, қашықтан оқыту, ақпараттық-коммуникациялық технологияларды енгізу және тиімді пайдалану білім берудің міндетіне жатады. «Сапалы білім беру Қазақстанның индустриалдық-инновпациялық дамуыныі негізі болуы тиіс», -деп атап өтті ҚР-ның президенті [1] .

Математиканың әр қадамы өмірдің қажетінен туады, сабақта қарастыратын көп есептер адамның практикалық дүниесіне байланысты. Сондықтан математикалық ұғымдардың нақты және тиімді болуы оқушылардың жеке тәрбиесіне байланысты, оқу жүйесіне қойылатын бірінші шарт - ол оқушылардың оқу процесі өмірімен байланысты болуы. Математикадан алған білім, біліктерін оқушылар тек еңбек және оқу әрекеттерінде қолданып қоймай, сонымен қатар мәдениеттің басқа салаларында меңгертуге де пайдалануға болады. Математиканың тәрбиелік әсер етуі - оқушылардың бойында ой - өрісті, саналы ойлай білу ерекшеліктерін, өмірге деген көзқарастарын, танымдық ерекшеліктерін, патриоттық сезімдерін оята отырып дамыту, қалыптастыруда үлкен роль атқарады. Ал, ондай жетістіктерге алгебралық материалдарды жетік меңгеру арқылы жеткізу мүмкін .

Дұрыс жолға қойылып шешілетін математикалық білім оқушының бойында өте бекем, орнықты ойлау қабілеттері мен дағдыларын қалыптастырады. Ешқандай, математикадан өзге пәндік сабақтар, оқушыға «дұрыстылық, дәлдік, әділеттілік» секілді бейтанысты тенденцияны ашып айқындап көрсете алмайды [2] .

Математиканы оқытуда, біздіңше, дамыта оқытуды қалыптастыру мен дамыту жолдарын анықтаудың негізі ретінде оқушының жеке басының іс-әрекеттін қасиетіне деген қызығушылықтың ыңғайынан алған абзал.

Дамыта оқыту - оқушылардың танымдық сұранысының нысанивті көрінісі ретінде, яғни олардың шығармашылық есептерді орындауда білімі, біліктілік және машақтарға ие болуларына бағытталған қауырт оқу танымдық іс-әрекеті ретінде көрінеді. Осындай іс-әрекетті басқаратын, қарастырылып отырған математикалық жағдайдың (ол әртүрлі есеп, тапсырмалар, мәселеліқ мәселелер болуы мүмкін) шешімін табуда оқушының іс-әрекетінің шығармашылық сипатында өрбуіне жетелейтін әдістемені жасау қажеттілігінен туып отыр.

Осы айтылғандардың бәрі мектепте математиканы оқыту үдерісінде шығармашылық және логикалық есептерді біртұтас және жүйелі пайдалану арқылы оқушылардың дамыта оқытуында дамыту әдістемесін құрудың көкейтесті екенін көрсетеді.

Зерттеу нысаны: Бастауыш сыныптың математика сабақтарындағы дамыта оқыту үдерісі.

Зерттеу пәні: Бастауыш мектептің 4-сынып математикасы.

Зерттеудің мақсаты: 4-сынып математикасындағы алгебралық элементтерді дамыта оқытуды теориялық тұрғыда зерттеп, әдістемесін жасау.

Қойылған зерттеу мақсатына жету мен тексеру үшін зерттеу жұмысының төмендегідей міндеттерін шешу қажет болады:

Бастауыш математика мазмұнына жалпы сипаттама беру;
Бастауыш математикадағы алгебра элементтеріне жалпы түсініктеме

беру;

Дамыта оқыту технологиясының тиімділігін көрсету;
Дамыта оқыту технологиясын алгебра элементтерін оқытуда жолдарын

көрсету (4-сынып) ;

Есептерді шешуде алгебралық әдісті пайдаланудың маңыздылығы.

Зерттеу жұмысының әдіснамалық және теориялық негіздері: Жеке тұлға және оның іс-әрекеті, таным, білім, ақыл-ой, ойлау құндылықтары туралы психологиялық, педагогикалық теориялар мен тұжырымдамалар, білім сапасы және оны арттыру мақсатындағы алгебра элементтерін дамыта оқытудың алатын рөлі мен атқаратын қызметі.

Зерттеу көздері: ҚР «Білім туралы» заңы, философ, психолог, педагогтардың материалдары, әдістемелік нұсқаулықтар, бастауыш мектеп журналдары, педагогикалық шығармалар және оқу-тәрбие үдерісі.

Зерттеу әдістері: Оқушылардың ғылыми - дүниетанымдық қабілеттерін қалыптастыру, логикалық ойлау қабілеттерін дамыту, практикалық дағдылары мен ептіліктерін дамыту және т. б өзекті мәселелердің ішінде оқушылардың мектептің жоғарғы сыныптарындағы алгебра курсына дайындығын жетілдіру

Зерттеудің ғылыми болжамы: Егер бастауыш сыныпта оқушыларға алгебралық материалдарды дамыта оқыту технологиясы арқылы жетік меңгерте алсақ, онда олардың математикадан білім деңгейі жоғарылайды және т. б пәндерді оқушылардың жетелей түсінуіне, қазіргі заман талабына сай терең білім алуына ықпал жасайды.

Зерттеудің практикалық құндылығы: Бастауыш сыныпта математиканы оқыту әдістемесін жетілдіруде, бастауыш мұғалімдері мен әдіскерлердің іс-тәжірибесінде қолдануға болады.

Бастауыш математика курсын дамыта оқыту технологиясын қолданудың теориялық негізіБастауыш математика мазмұнына жалпы сипаттама

Қазіргі ғылыми-техникалық үдеріс жедел өсу кезеңінде, математиканың ролі артты, сондықтан математикалық білім қоғамдық зор маңызға ие болды.

Ғылыми-техникалық және әлеуметтік қауырт прогресс жағдайында мектептің ролі бұрын-соңды болмаған дәрежеде артатындығы, мектептің - басты міндеті оқушыларға ғылым негіздерінен берік білім беру екендігі, олардың жоғары санасезімін қалыптастыру екендігі өмірге дайындау, саналы түрде мамандық таңдап ала білуге дайындау екендігі және орта білім беруді жетілдіре түсу мақсатымен мектепте берілетін білім мазмұнын қазіргі кездегі ғылым, техника және мәдениет жетістіктері мен талаптарына сәйкес ғылыми негізделген оқу жоспарын және бағдарламасын енгізу керек.

Алға қойылған осы міндеттерді жүзеге асыру мақсатымен соңғы жылдары мектепте білім беруді қайта құру жөнінде үлкен
жұмыс істелді, соның нәтижесінде барлық пәндерден дерлік, оның ішінде математикадан да, жаңа бағдарлама енгізіліп, оқыту әдістері жетілдіре түсті. 1995 жылдан бастап мектептің бастауыш сыныптарында оқыту ісі жаңа бағдарламалар бойынша жүргізіле бастады.

Бастауыш сыныптардың математика жөнінен жаңа бағдарламаларға көшуіне байланысты жаңа әдістемелік жүйе жасалды, ол жүйе жаңа бағдарламаны іске асырудың тиімді жолдарын қарастырады. Мұндай жүйені жасау үстінде математиканы оқыту ісінде бұрыннан жинақталған құнды делінгендердің бәрі пайдаланылды.

Бастауыш сынып оқушыларына математиканы ойдағыдай оқыту үшін алғаш оқыта бастаған мұғалім математиканы оқытудың бұрыннан қалыптасқан жүйесін, бастауыш сыныптарда математиканы оқыту әдістемесін игеруі тиіс және осының негізінде ол өз бетімен шығармашылық жұмыс істейтін болуы керек [2] .

Математиканы оқыту әдістемесі ең алдымен төменгі сынып оқушыларына математиканы оқыту міндетін жалпы оқу
және тәрбие жүйесімен бірге қарастырады. Әдістемеде математиканың бастауыш курсының мазмұны мен құрылысы ашылып айқындалынады, яғни математикадан бастауыш сыныптарда қандай материал оқылатыны және неге дәл сол материал таңдап алынғандығы, курстың әрбір жеке мәселесі бастауыш сыныптарда қандай дәрежеде жинақталып оқылатыны, курс тақырыптары қандай тәртіпте қарастырылатыны және мұндай тәртіптің неге анағүрлым тиімді екендігі айтылады. Математиканы бастауыш сыныптарда оқыту әдістемесінде курстағы әрбір тарауды және сол тараудағы әр мәселені (мысалы, 10 көлеміндегі сандарды қосу мен азайтуды қалай оқып үйрену керектігі, атап айтқанда, осы тақырыпта қосудың ауыстырымдылық қасиетін анықтау) оқып үйренудін дербес әдістері айқындалады. Математиканы оқыту әдістемесі оқушыларға теориялық білімді игеру, алған білімін алуан түрлі практикалық мәселелерді шешу үшін қолдана білуге үйрену, оқушыларда берік дағды қалыптастыру жөнінде дәлелді ақыл-кеңестер ұсынады. Сондай-ақ методикада математиканы оқытуда зор нәтижеге жету үшін балалардың оқу ісін қалай ұйымдастыру керектігі жөніндегі мәселелер айқындалады. Оқыту тәрбие беру сипатты екендігі белгілі, олай болса, әдістеменің міндеті - жаңа адамды тәрбиелеуге оқушылардың ақыл-ойының жетіліп дамуына көмектесетін оларды математикаға қызықтырып ынталандыратын мінез-құлқынын жақсы болып қалыптасуына көмектесетін оқыту әдістерімен мұғалімді қаруландыру.

Математиканы оқыту әдістемесі жоғары оқу орнында өтілетін басқа пәндермен тығыз байланысты.

Математиканы оқыту әдістемесі ең алдымен өзінің негізі математика ғылыммен табиғи байланысты. Математиканың мектепте өтілетін курсы мазмұнын таңдап алуда математика ғылымының өз деңгейі әрқашан әсерін тигізіп отырады: белгілі бір уақыт кезеңінде математиканың қандай идеялары жетекші болатынына қарай материалдың мазмұны іріктеп алынады да, енгізіліп отырған ұғымның қайсыбір түсініктемелері (трактовкасы) беріледі. Математиканы оқыту әдістері математиканың бастауыш курсында айқындалатын идеяларына байланысты болады. Әдістемені терең ұғынып оны мектеп тәжірибесінде шығармашылықпен қолдануда мұғалімнің математика курсын жақсы білуі және ең негізгі математикалық ұғымдардың қазіргі кездегі түсініктемелерімен таныс болуы талап етіледі.

Математиканы оқыту әдістемесі педагогикамен және педагогикалық психологиямен тығыз байланысты. Математика курсын құруда, математиканы оқыту әдістемесін таңдап алуда, математиканы оқыту мақсаттары мен міндеттерін белгілеуде математика әдістемесі педагогика мен педагогикалық психологияда айқындалған жалпы оқыту заңдылықтарына сүйенеді. Педагогика немесе психология ашып берген оқытуға қатысты жаңа заңдылыктар әдістемеде де әрқашан әнгіме болады. Әдістеменің дербес қағидалары педагогикалық және психологиялық тұжырымдар үшін материал болып табылады. Мұғалім әрбір әдістемелік әдістен, жаттығулар жүйесінен педагогикалық және психологиялық зандылықтардың, көрінісін байқап отырса, әрбір сабақты талдау кезінде соларға сүйеніп отырса, әрбір оқушы терең білім алатындай дәрежеге жетуге ат салысып, сол зандылықтарды пайдаланып отырса, сонда ғана методиканы саналы түрде игеріп, дұрыс қолдану мүмкін болады. Математиканы оқыту әдістемесін төменгі сынып оқушыларына білім және тәрбие беру міндеттерін шешуде, басқа әдістемелермен (қазақ тілін оқыту, еңбекке тәрбиелеу, сурет салу әдістемесі т. с. с. ) көптеген ортақ мәселелері бар. Пәнаралық байланыстарды дұрыс іске асыру үшін, мұғалімнің мұны ескеруі өте қажет.

Математиканы оқыту әдістемесі мұғалімдердің озат тәжірибесінің қорытындысы ретінде тарихпен қатарласа қалыптасып келеді. Казіргі кезде сол тәжірибе қорытындысы да пайдаланылып отыр, бірақ негізге алынып отырғаны басқа материал математиканы оқытудың жаңа әдістері ғылыми зерттеудің нәтижесі болып отыр, өйткенде математика ғылымының өзіндегі жаңа бағыттар мен психология педагогикалық зерттеулердің табыстары ескеріледі Ғылыми зерттеулердің нәтижелері алдымен жеке мұғалімдердің іс тәжірибелерінде тексеріледі, ал содан кейін тиімді болып табылған әдістер көпшілік мектептерде енгізіледі [3] .

Мектепте математиканы оқыту, кез келген басқа пәндерді оқыту сияқты, білім беру, тәрбиелік және практикалық міндеттерді шешетін болуы тиіс.

Математиканы оқып үйрену үдерісінде оқушылар бәрінен бұрын теориялық білімдер жүйесін меңгеруі, сондай-ақ бағдарламада көрсетілген бірқатар біліктер мен дағдыларды игерулері қажет. Оқыту ісі оқушылардын саналы білім алуын және де жеткілікті жоғары дәрежеде қорыта білуін қамтамасыз ететін болуы керек. Егер оқыту ісі жетілдіріліп отырса, яғни оқушылардың интеллектуалдық даму дәрежесі, олардың танымдылық қабілеті және ынтасының дамуы жеткілікті қамтамасыз етілсе, жоғарыда айтылғандарды іске асыруға мүмкіндік болады.

Математиканы оқыту кезінде оқушыларда материалистік көз қарастың бастамасы қалыптаса бастайды. Сан арифметикалық амалдар, санау жүйесі, геометриялық фигура т. с. с. математикалық алғашқы ұғымдар берілетін бастауыш сыныптардың өзінде-ақ оқушы «математиканың нысанасы - шын дүниенін кеңістік формалары мен сандық қатынастары екенін, демек, мұнын өзі реалдық материал екенің» сол сияқты «сан мен фигура ұғымдары біржақтан алынбағаның нақты дүниеден алынғанын» оқушы түсініп білуге тиіс. Сондықтан математиканы оқытудың өмірмен байланысын жүзеге дұрыс асыра білу өте маңызды жұмыс. Бір жағынан, мектеп оқушыларын бізді қоршаған өмір құбылыстарынан математикалық фактілерді (абстракцияларды) тани білуге үйрету, екінші жағынан, математиканы нақтылы практикалық есептерді шешу үшін қолдану, әрбір адамға күнделікті өмірде қажет болатын практикалық білімдермен оқушыларды қаруландыру мысалы: есептеуді немесе өлшеуді орындау, онша күрделі емес есеп-қисапты шығару т. с. с.

Математиканы оқыту ісі өз Отанын (елін) сүйетін біздің қоғамымыздың игі мақсаттарын сезіне білетін өз білімін коғамдық мұраттарды жүзеге асыру үшін сарып етуге дайын қоғам адамдарын тәрбиелеу міндетін жүзеге асыруға көмектесуі тиіс.

Математиканы оқыту жеке адамның енбек сүйгіштігі, ұқыптылығы сияқты ерекшеліктерін қалыптастару міндетін шешіп, оқушылардың еркін, зейінін, қиялын қамтуға барынша мүмкіндік жасауы тиіс математикаға деген ынтасын арттыруға көмектесуі тиіс. Балаларды оқи білуге төселдіру, оларды белгілі бір материалмен жұмыс істей білуге үйрету және өз беттерімен жұмыс істеуге дағдыландыру қажет.

Математиканы бастауыш сыныптарда оқыту оны әрі қарай 9-11 сыныптарда оқып білу үшін оқушылардың білімі мен дағдысына, сол сияқты ой-өрісінің дамуына сенімді негіз болуы тиіс [4] .

1-4 сыныптарға арналған математика бағдарламасының «Түсінік хатында» былай делінген: «Оқыту мен тәрбиелеуді оқушылардың білімді игеруі мен танымдылық қабілеттерін дамытуды табиғи үйлестіру; білімнің теориялық денгейін арттыру және алған білімді практикада қолдана білуге дағдыландыру; ол үшін қажетті дағдылар қалыптастыру, міне, математиканы мектептің төменгі сыныптарында оқытуда жетекші негіз болып табылатындар осылар. 1-4 сыныптарда математиканы оқыту мазмұнын іріктеп алу, сол материалды белгілі бір жүйемен орналастыру, математиканы оқыту әдістерін таңдау математиканы оқытудың негізгі міндеттерін шешуге бағындырылуы тиіс.

1-4 сыныптарда оқылатын математиканың бастауыш курсы математиканың мектептік курсының табиғи бөлігі болып табылады. Демек, 5-11 сыныптарда өтілетін математика курсы бастауыш курстың жалғасы, ал бастауыш курс оның бастапқы негізі болып табылады. Осыған сәйкес математиканың бастауыш курсына теріс емес бүтін сандардың және негізгі шамалардың арифметикасы, алгебра мен геометрия элементтері енеді [5] .

Математиканың бастауыш курсы құрылысының өзіндік ерекшеліктері бар.

Бірінші ерекшелігі . Курстың негізгі мазмұны арифметикалық материал болып табылады. «Натурал сандар мен негізгі шамалар арифметикасы бастауыш курстың негізі болады. Сонымен бірге оған геометрия мен алгебралық пропедевтика элементтері енеді, бұлар мүмкіндігінше сан арифметикалық амалдар мен математикалық қатынастар жөніндегі ұғымдардың барынша жоғарғы дәрежеде игерілуіне көмектесе отырып, мүмкіндігінше арифметикалык білімдер жүйесіне енеді, яғни алгебра мен геометрия элементтері математика курсының ерекше жеке тарауы бола алмайды, арифметикалық материалмен табиғи байланыста болады. Осындай байланыс, бір жағынан, балаларды алгебра және геометрия идеяларымен ертерек таныстыруға, екінші жағынан, төменгі сынып оқушыларының арифметикалық білімді неғұрлым жоғары дәрежеде игеруіне мүмкіндік береді.

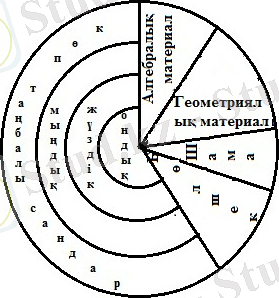
Екінші ерекшелігі . Бастауыш курс материалы шоғырланған түрде беріледі. Ең алдымен ондық бөлшектеуге келмейтін алғашкы он санның нумерациясы оқылады, осы сандарды жазу үшін цифрлар енгізіледі, қосу және азайту амалдары үйреніледі. Сонан сон екінші ондық және 100 көлеміндегі сандардың нумерациясы қарастырылады, разряд ұғымы, ондық бөлшектеуге келетін сандарды жазудың позициялық принципі айқындалады, екі таңбалы сандарды қосу және азайту оқылады, жаңадан арифметикалық екі амал; бөлу және көбейту енгізіледі. Бұдан кейін 1000 көлеміндегі сандар нумерациясы үйреніледі. Мұнда көп таңбалы сандар нумерациясының негізін құрайтын үш разряд (бірліктер, ондықтар, жүздіктер) қарастырылады, арифметикалық амалдар жөніндегі білім жинақталып қорытылады, жазбаша қосу мен азайту әдістері енгізіледі. Ақырында, көп таңбалы сандар нумерациясы үйреніледі, класс ұғымы қарастырылады, цифрлардың 1-сурет орындық мәнінін принципі жөніндегі білетіндері жинақталып қорытылады, жазбаша есептеулер алгоритмі енгізіледі. Сонымен, курста бес концентр бөлініп алынған: ондық, екінші ондық жүздік, мың, көп таңбалы сандар. Нумерацияны және арифметикалық амалдарды қарастырумен бір мезгілде және тығыз байланыста басқа да мынадай мәселелер қарастырылады: шамалар, бөлшектер, алгебралық және геометриялық материал. Материалдың концентрлі орналасуы 1-суретте сызба түрінде берілген.

Осындай концентрді айырып бөлудін өзі санаудың ондық жүйесіның және есептеу әдістерінің мынадай ерекшеліктерімен түсіндіріледі: әрбір концентрде есептеу жүйесімен және арифметикалық амалдармен байланысты жаңа мәселелер айқындалады. Тәжірибе көрсеткендей, материалдың концентрлі орналасуы, сызықтық орналасуына қарағанда төменгі класс оқушыларына көбірек лайықтырақ: математиканы оқыту балалардың шама-шарқына лайықты және оларға мектепке дейін белгілі сандардың шағын көлемінен басталады, сандардың бұл аймағы бірте-бірте кеңейтіле беріледі, біртіндеп жаңа ұғымдар енгізіледі. Курстың мұндай құрылысы жүйелі қайталап отыруды және сонымен бірге оқып білгенді тереңдете түсуді қамтамасыз етеді, өйткені бұрын үйренген білім мен білік, дағды сандардың жаңа көлемінде қолданылады. Осының бәрі курсты жақсырақ игеруге көмектеседі.

Үшінші ерекшелігі . Теория мәселелері мен практикалық сипатты мәселелер бірімен-бірі табиғи байланыста болады. Теорияның көптеген мәселелері индуктивті түрде енгізіледі ал практикалық сипатты мәселелер соларға негізделіп айқындалады. Мысалы, көбейтудің үлестірімділік қасиеті дербес фактілерді жинақтап қорытындылау негізінде енгізіледі де осы қасиет пайдаланылып көбейту әдісі ашып көрсетіледі.

17*3=(10 + 7) *3=10*3+7*3=51.

Осындай өзара байланыс кезінде теориялық мәселелер жақсы игеріледі және саналы түрде практикалық іскерлік қалыптасады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.