Бірқалыпты теңдеу жүйелері: сұраныс-ұсыныс моделі, идентификация және бағалау әдістері


11-Лекция. Бірқалыпты теңдеулер жүйесі
Жоспары:
11. 1. Бірқалыпты теңдеу жүйесінің жалпы түрі Сұраныс және ұсыныс моделі.
11. 2. Ең кіші квадраттық жанама тәсіл.
11. 3. Идентификация проблемалары.
11. 4. Инструментальды айнымалылар тәсілі.
11. 5. Бірқалыпты регрессионды теңдеуді бағалау. Сырттай байланыспаған теңдеулер.
11. 6. Ең кіші квадраттық үшөлшемді тәсіл.
Мақсаты: Бірқалыпты теңдеулер жүйесінің жалпы түрлерін, ең кіші квадраттық жанама тәсілін түсіну. Идентификация проблемаларын, инструментальды айнымалылар тәсілін анықтау. Бірқалыпты регересионды теңдеулерді бағалау әдістерін сиаптитайтын көрсеткіштерді анықтау.
Тақырып бойынша негізгі ұғымдар: Бірқалыпты теңдеулер, сұраныс пен ұсыныс моделі, эндогенді және екзогенді айнымалылар, матрица теңдеуі, ең кіші квадраттық жанама тәсіл, структуралық форма (құрылымдық қалып), құрылымдық параметрлер, идентификация проблемалары, идентифицирленген және идентифицирленбеген жүйе, инструментальды айнымалылар тәсілі, сырттай байланыспаған теңдеулер.
Бірқалыпты теңдеу жүйесінің жалпы түрі. Сұраныс және ұсыныс моделі
Коррелировантты регрессордың бір себебі болып, кездейсоқ мүшелер факторлары атқаруы мүмкін, бірқалыпты жұмыс істейтін регрессорлардың өздері, түсіндірмелі ауысымды регрессорлардың фиксированды мағынасында болады. Басқа сөзбен айтқанда, қарастырылған экономдық жағдайда түсіндірілген ауысымды мағыналардың және регрессорлардың қалыптасуы сыртқы факторлар әсерінен болады. Бұл дегеніміз қарастырып отырған модель толық емес, ондағы ауысымдар ретінде регрессорлар шықса, онда оны теңдікпен толықтыру қажет. Сондықтан бізге бірқалыпты жүйелерді немесе регрессионды теңдеулерді қарастыруға тура келеді.
Классикалық мысал ретінде бірқалыпты сұраныстың қалыптасуы Q d және ұсыныс Q s тауары оның бағасымен байланысты P жатады:
Q
d
=
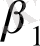 +
+
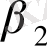 P+
P+
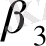 I+
I+
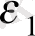 ; (11. 1)
; (11. 1)
Q
s
=
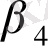 +
+
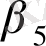 P
+
P
+
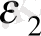 ;
;
мұндағы I-табыс.
Егер біз нарықты тепе-теңдік жағдайында деп ескерсек, онда теңдікті Q d =Q s =Q деп жалғастыру керек. Бұл жағдайда қарастырып отырған Р-бұл тепе-теңдік бағасы, бұндағы сұраныс пен ұсыным бірқалыпты қалыптасады. Сөйтіп, біз P және Q-ді түсіндірмелі ауысымдар деп, ал табыс көлемін I-түсіндірмелі ауысым деп есептеуіміз қажет.
Бірқалыпты теңдеу жүйелеріндегі айнымалылар арасындағы ролдердің бөлінуі келесі түрде жіктелінеді : Q және P ауыспалылары өз мәндерін (11. 1) теңдеуіне бағынып, яғни модель ішінде қалыптасады. Бұндай айнымалылар эндогенді деп аталады. (11. 1) теңдеуінде I айнымалылары берілген болып саналады, ал оның мағынасы моделден тыс қалыптасады. Бұндай айнымалылар экзогенді деп аталады.
Математикалық көзқараспен қарағанда, экзогенді және эндогенді айнымалылар арасындағы басты айырмашылық бұл экзогенді айнымалылар регрессия қателіктерімен коррелинденбейді, ал эндогенді айнымалылар коррелинденеді. Кездейсоқ ұқсас факторлар тепе-теңдік бағасына, тауар сұранысына әсерін тигізеді. Айнымалылар арасындағы тәуелділіктер олардың кез-келген мүшелерімен коррелинденуіне әкеп соғады. Экзогенді айнымалылар жиынтығы әр түрлі болуы мүмкін. Мысалы, сұраныс және ұсыныс моделдері ретінде экзогенді айнымалылар табысына проценттік қойылым, уақытша тренд және т. б қосылуы мүмкін.
Бірқалыпты теңдеу жүйесінің жалпы түрін қарастырсақ: Ү 1, . . . Ү m -эндогенді айнымалылар болсын, ал Х 1 , . . . , Х l -экзогенді айнымалылар. В және Г блоктық матрицалар түрін келтірейік:
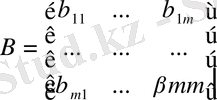
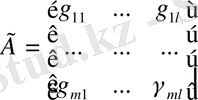 .
.
Онда бірқалыпты теңдеу жүйесінің жалпы түрі матрицалық формада былайша ұсынылады:
BY+ГХ=
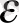 , (11. 2)
, (11. 2)
бұнда
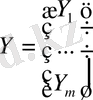
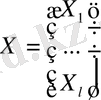
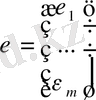
Регрессионды теңдеуден басқа модель теңсіздік құрауы мүмкін, бұнда эндогенді айнымалылар өз ішінде алгебралық байланысты көрсетеді. Мысалы, сұраныс және ұсыныс бағалық тепе-теңдік моделін қалыптастыру үшін екі сәйкес келетін (11. 1) теңдеуін аламыз және Q s =Q d теңсіздігі.
Жалпы айтқанда, теңдік кейбір эндогенді айнымалыларды және регрессионды теңдеу жүйелерінің кіші өлшемін ерекшелеуге мүмкіндік береді. Сондықтан, сұраныс және ұсыныс моделінде (11. 2) структуралық формасын қалыптастыруға және Q s =Q d =Q теңдеуін қоюға болады, яғни
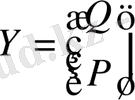
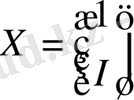
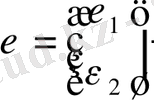
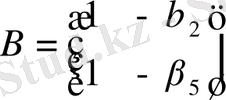
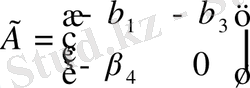
Бұл тарауда біз екі эндогенді айнымалылар теңдеуіне тоқталамыз. Бұл ешқандай маңызды шығын келтірмейді, барлық керекті теория аспектілерін осы қарапайым жағдайда қадағалауға болады. Осы кезде бұндай шектеу бізге есептеулердегі керексіз жинақтаулардан арылуға мүмкіндік береді.
Бізге әруақытта эндогенді айнымалыларды жүйенің сол жақ бөлігінен ерекшелеп алуымызға болады, яғни теңдеуді мынадай түрде жазуға болады:
Y=
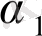 +
+
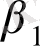 X
1
+
X
1
+
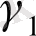 Y
2
+
Y
2
+
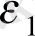 ; (11. 3)
; (11. 3)
Y
2
=
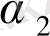 +
+
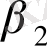 X
2
+
X
2
+
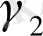 Y
1
+
Y
1
+
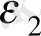 ; (11. 4)
; (11. 4)
Х
1
және Х
2
айнымалылар жиынтықтары еркін түрде болуы мүмкін. Жалпы айтқанда,
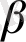 параметрлері векторлы. Егер (11. 3), (11. 4) теңдеулеріне қарапайым ең кіші квадраттық тәсілін қолданса, онда 6 тарауда көрсетілгендей керексіз бағалар параметрлері
параметрлері векторлы. Егер (11. 3), (11. 4) теңдеулеріне қарапайым ең кіші квадраттық тәсілін қолданса, онда 6 тарауда көрсетілгендей керексіз бағалар параметрлері
 ,
,
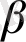 ,
,
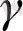 шығады. Осылайша, бірқалыпты теңдеу жүйесін бағалауға арнайы тәсілдер қажет етіледі.
шығады. Осылайша, бірқалыпты теңдеу жүйесін бағалауға арнайы тәсілдер қажет етіледі.
Ең кіші квадраттық жанама тәсіл
Ұсынылған тәсілдің негізінде қарапайым пікір жатыр. Ең кіші квадраттық тәсілдерді қолданудағы ең басты кедергісі болып, кездейсоқ мүшелердің эндогенді айнымалылар коррелированттылығы табылады, сондықтан Х экзогенді айнымалылар теңдеуінің оң жағында қалу үшін, Y-ті теңдеу жүйесіне қатысты деп алу керек. (11. 3), (11. 4) теңдеуіне қолдануға болады. Алынған теңдеуге қарапайым ең кіші квадраттық тәсілді қолданып және кейбір шығыс параметрлері үшін бағалаулар алу, одан кейін параметрлердің өздерінен бағалауларды табу.
Бұндай процедура ең кіші квадраттық жанама тәсіл деп аталады. Бұл жүйені (11. 3) -(11. 4) теңдеу мысалында қарастырамыз.
Y 1 , Y 2 -ге қатысты етіп (11. 3) -(11. 4) теңдеулерін мына түрде жазамыз:
Y
1
=
a
1
+
b
1
X
1
+
c
1
X
2
+
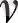 1
; (11. 5)
1
; (11. 5)
Y
2
=
a
1
+
b
2
X
1
+
c
2
X
2
+
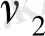 ;
;
мұнда
a
1
=
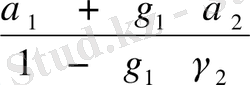
 ;
a
2
=
;
a
2
=
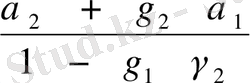 ;
b
1
=
;
b
1
=
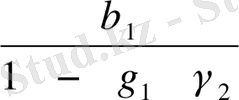 ;
b
2
=
;
b
2
=
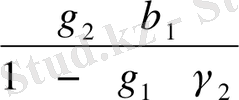 ;
;
c
1
=
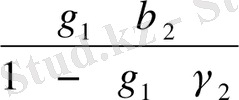 ;
c
2
=
;
c
2
=
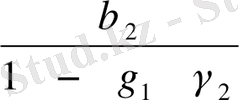 ;
;
 =
=
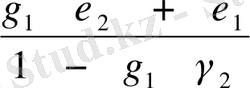 ;
;
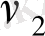 =
=
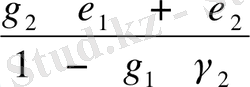 ; (11. 6)
; (11. 6)
Одан әрі ыңғайлылыққа Ү айнымалылар орталықтандырылған деп есептесек, онда а=0. (11. 5) -ке қарапайым ең кіші квадраттық тәсілді қолданып, b, c бағалау параметрлерін аламыз.
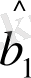 =
=
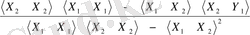 ;
;
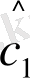 =
=
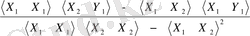 ; (11. 7)
; (11. 7)
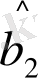 =
=
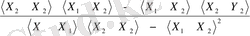 ;
;
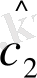 =
=
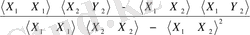 ;
;
мұнда

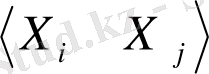 =
=
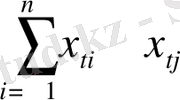 ,
,
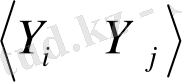 =
=
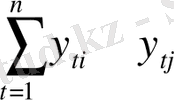 ,
,
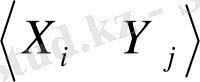 =
=
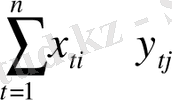 ,
,
x tj , x tj , y ti , y tj - X i , X j , Y i , Y j айнымалылар мағынасы
(11. 6) теңдігі α, β, γ шығыс параметрлері a, b, c арқылы бір мәнді білдіреді:
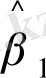 =
=
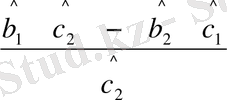 ;
;
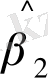 =
=
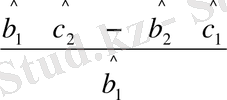 ; (11. 7)
; (11. 7)
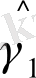 =
=
 ;
;
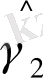 =
=
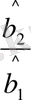 ;
;
Солайша, (11. 8) теңдігін қолданып, мынаны аламыз:
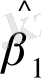 =
=
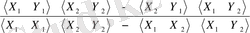 ;
;
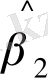 =
=
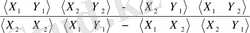 ; (11. 9)
; (11. 9)
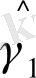 =
=
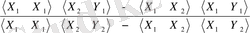 ;
;
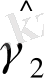 =
=
 ;
;
(11. 8) бағалаулары ең кіші квадраттық жанама тәсілдің бағалаулары деп аталады. Ең кіші квадраттық тәсілдің тікелей қолданудағы бағалардың өзгешелігі ол (11. 9) бағалаулары толық мәнді болып келеді.
(11. 3) -(11. 4) жүйені зерттеу мысалын қарастырайық. Қарастырып отырған айнымалылардың берілгені n=200 деп алынсын.
Бірінші қарапайым ең кіші квадраттық тәсілді қолданамыз. Одан мынадай нәтиже аламыз:
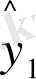 =3153, 451+15, 73x
1
- 1, 2y
2
; d=1, 894, R
2
=0, ;
=3153, 451+15, 73x
1
- 1, 2y
2
; d=1, 894, R
2
=0, ;
(5, 127) (0, 687) (0, 001)
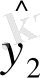 =2606, 23+12, 88x
2
-0, 83y
1
; d=1, 893, R
2
=0,
=2606, 23+12, 88x
2
-0, 83y
1
; d=1, 893, R
2
=0,
(1, 75) (0, 581) (0, 001)
Екі жағдайда да біз практикалық жүзпроценттік нәтиже аламыз: төртінші белгіге дейін детерминация коэффиценті дәлдікпен бірге тең. Бірақ, біз білетіндей алынған бағалаулар толық емес, сондықтан олардың мәндері нақты параметрлер мәндерінен ауытқуы мүмкін.
Енді ең кіші квадраттық жанама тәсілді қолданып, Ү i -дан Х 1 -ге және Х 2 -ге регрессионды тәуелділігін бағалаймыз:
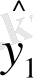 =2242, 755+471, 19x
1
-241, 07x
2
; d=1, 96, R
2
=0, 778,
=2242, 755+471, 19x
1
-241, 07x
2
; d=1, 96, R
2
=0, 778,
(361, 2) (19, 04) (28, 83)
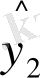 =727, 7-376, 37x
1
+201, 29x
2
; d=1, 96, R
2
=0, 769,
=727, 7-376, 37x
1
+201, 29x
2
; d=1, 96, R
2
=0, 769,
(297, 35) (15, 67) (23, 74)
Осылайша мынаны аламыз:
b 1 =471, 19; c 1 =-241, 07; b 2 =-376, 37; c 2 =201, 29; (11. 10)
a 1 =2242, 755; a 2 =727, 7,
одан (11. 8) -ді қолданып, мынаны аламыз:
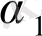 =3114, 286;
=3114, 286;
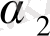 =2519, 134;
=2519, 134;
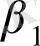 =20, 43;
=20, 43;
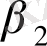 =8, 73; (11. 11)
=8, 73; (11. 11)
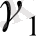 =-1, 198;
=-1, 198;
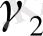 =-0, 8
=-0, 8
Көріп тұрғандай, бұндай жолмен шыққан бағалаулар айырмашылығы ең кіші квадраттық тәсілден гөрі тез білінеді.
Идентификация проблемалары
Қарастырып отырған мысалда (11. 6) теңдеуі шығыс параметрлеріне қатысты бірмәнді, бұнда олардың толық бағалауларын табуға мүмкіндік береді. Бұндай жағдай әрқашан орын таба бермейді. Бұл проблемаларды тереңірек қарастырайық.
Теңдеу жүйесінің (11. 2) формасы структуралық форма деп аталады. Белгісіз структуралық екі формасы бар екі теңдеуді де (11. 3) - (11. 4) теңдеулері деп атайды. Структуралық форма параметрлері структуралық параметрлер деп аталады. (11. 5) формасы деп жүйеде келтірілген форма аталады. Келтірілген форма параметрлері ең кіші квадраттық тәсіл көмегімен анықталады. Бірақ экономикалық мағынаға және анализге деген қызығушылықты структуралық форма параметрлері көрсетеді. Дәл осы структуралық форма эндогендік айнымалылардың экономикалық механизм мағынасын ашып қарастырады.
Идентифицирленген деп структуралық параметр аталады, егер ол ең кіші квадраттық жанама тәсіл көмегімен бірмәнді деп анықталса.
Т еңдеу идентифицирленеді, егер оған кіретін барлық структуралық параметрлер идентифицирленген болса.
Идентифицирленбеген деп структуралық параметр аталады, егер формада келтірілген параметрлердің нақты мәнін білсе де оның мәнін ала алмаса. Соңында, параметр аса идентифицирленген деп аталады, егер ең кіші квадраттық жанама тәсілінің бірнеше бағалауларын білсе.
Мысалы, қарастырып отырған моделдерде Ү 1 айнымалысын екі экзогенді Х 1 , Х 2 айнымалысына тәуелді Ү 2 деп ұсынсақ, Ү 2 -ні динамика сияқты эндогенді Ү 1 айнымалысы анықтайды, яғни теңдеу жүйесі мына түрді береді:
Y
1
=
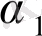 +
+
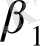 X
1
+
X
1
+
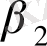 X
2
+
X
2
+
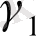 Y
2
+
Y
2
+
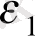 ; (11. 12)
; (11. 12)
Y
2
=
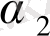 +
+
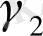 Y
1
.
Y
1
.
Келтірілген формада (11. 12) теңдеуі мынадай (11. 5) теңдеуін береді, бұнда
b
1
=
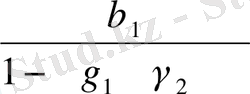 ;
b
2
=
;
b
2
=
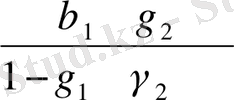 ; (11. 13)
; (11. 13)
c
1
=
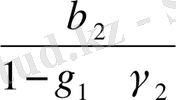 ;
c
2
=
;
c
2
=
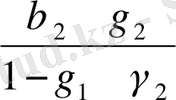 ;
;
мүмкін мына түрде жазылады:
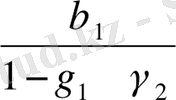 =
b
1
,
=
b
1
,
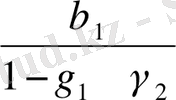 =
c
1
, (11. 14)
=
c
1
, (11. 14)
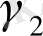 =
=
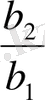 =
=
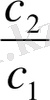 . (11. 15)
. (11. 15)
(11. 14) екі теңдеуінен
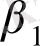 ,
,
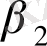 ,
,
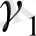 үш коэффиценті табылуы мүмкін еместігі анық. Бұл шексіз көп ықтимал мәндер бірінші келтірілген және содан кейінгі келтірілген формада бар екенін білдіреді. Бұндай коэффиценттер идентифицирленген деп аталады және оған қатысты идентифицирленген деп параметрлері бар теңдеу аталады.
үш коэффиценті табылуы мүмкін еместігі анық. Бұл шексіз көп ықтимал мәндер бірінші келтірілген және содан кейінгі келтірілген формада бар екенін білдіреді. Бұндай коэффиценттер идентифицирленген деп аталады және оған қатысты идентифицирленген деп параметрлері бар теңдеу аталады.
Осы кезде біз
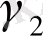 -ны анықтау үшін екі әртүрлі (11. 15) байланысымен берілген мүмкіндікті пайдаланамыз. Бұдан кейін біз теңдікті шығарамыз:
-ны анықтау үшін екі әртүрлі (11. 15) байланысымен берілген мүмкіндікті пайдаланамыз. Бұдан кейін біз теңдікті шығарамыз:
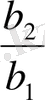 =
=
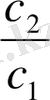 .
.
Бірақ бұл теңдік b және c параметр мәндеріне қолданылады, ал олардың бағалауларына ол әрине қолданылмайды.
Мысал ретінде, (11. 12) моделін берілгендерімен қарастырайық. Моделде келтірілген бағалаулар параметрлері (11. 10) мәндерін береді.
Осыдан аламыз:
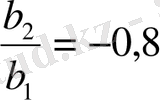
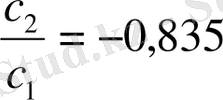
Аса идентифицирленген дегеніміз формада келтірілген коэффиценттер үшін бірнеше тәсіл мағыналары арқылы қолданылатын параметр. Қарастырып отырған мысалдағы
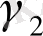 параметрі осындай болып табылады. Аса идентифицирленген проблема - бұл бақылаулар санының проблемасы: ұзындық көлемімен барлық әртүрлі толық бағалаулар параметрі нақты және сол дәл мағынасына ұмтылады.
параметрі осындай болып табылады. Аса идентифицирленген проблема - бұл бақылаулар санының проблемасы: ұзындық көлемімен барлық әртүрлі толық бағалаулар параметрі нақты және сол дәл мағынасына ұмтылады.
Идентифицирленбеген бұл анда-санда кездесетін құбылыс болып табылмайды. Шын мәнісінде, идентификацияға структуралық параметр бағалаулар саны формада бағаланып кеткен параметрлер санына тең болу керек.
Ең кіші квадраттық жанама тәсілдің қолданылмайтындығын идентифицирленбеген модельдер білдіреді. Келесі параграфтарда біз бірқалыпты теңдеу жүйесін бағалаудың басқа тәсілдерін қарастырамыз.
Инструментальды айнымалылар тәсілі
Инструментальды айнымалылар тәсілі - кеңірек тараған тәсілдер теңдеуін бағалау, ондағы регрессорлар жай мүшелермен коррелирленеді. Дәл осы бірқалыпты теңдеу жүйесінің белгісі болып табылады. Біз идентифицирленген және идентифицирленбеген жүйені екі бөлек қарастырайық:
1. Идентифицирленген жүйе
(11. 5) моделін қарастырайық. Оның коэффиценттеріне ең кіші квадраттық тәсіл (11. 8) бағалауларын береді. Бұл бағалаулар инструментальды айнымалылар тәсіл теңдеуінде алынған бағалаулармен сәйкес келетінін көруге болады
Y
1
=
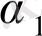 +
+
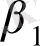 X
1
+
X
1
+
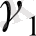 X
2
+
X
2
+
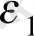 ; (11. 16)
; (11. 16)
Y
2
=
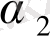 +
+
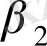 X
2
+
X
2
+
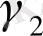 X
1
+
X
1
+
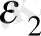 ;
;
Солайша, х 1 және х 2 экзогенді айнымалылар Ү 1 , Ү 2 -ге инструментальды айнымалылар ретінде қолданылады. Егер инструментальды теңдеу бағалауында инструментальды айнымалылар ретінде экзогенді айнымалылар қолданса, онда бұдан алынатын бағалаулар ең кіші квадраттық жанама тәсіл бағалауларымен сәйкес келеді.
Бұдан, ең кіші квадраттық жанама тәсілі инструментальды айнымалылардың кездейсоқ мүшесі болып табылады. 6 тарауда айтылғандай, практикада инструментальды айнымалылар тәсілі ең кіші квадраттық екіөлшемді формасы ретінде қолданылады. Бағалау кезінде келтірілген форма Ү
1
, Ү
2
айнымалысы
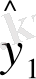 ,
,
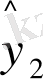 түсіндірмелі мағынасы инструментальды айнымалы ретінде қолданылады. Одан кейін бұл мағыналар (11. 5) оң жақ бөлім структуралық формалар ретінде қойылады.
түсіндірмелі мағынасы инструментальды айнымалы ретінде қолданылады. Одан кейін бұл мағыналар (11. 5) оң жақ бөлім структуралық формалар ретінде қойылады.
Ең кіші квадраттық жанама тәсіл бағалаулары екіөлшемді тәсіл бағалауларымен сәйкес келеді, Ү эндогенді айнымалы саны х экзогенді айнымалы санымен сәйкес келеді, егер жүйе теңестірілген болса.
2. Теңестірілмеген жүйе
Бұл жағдайда инструментальды айнымалы тәсілі, жалпы айтқанда, экзогенді айнымалылар жетіспейді - «сырттай» инструментальды айнымалыларын қолдану үшін оларды міндетті түрде орналастыру қажет.
Әртүрлі наборлар қолдану мүмкіндігіне ие,
l
санында инструментальды айнымалы шығынына ие деп ұйғарсақ. Бұл жағдайда екіөлшемді ең кіші квадраттық тәсіл қолайлы таңдауды көрсетеді. Инструментальды айнымалы наборы -
 болсын. Z кеңістігінің ауыспалы проекциясының эндогені - у
i
(оны шығару үшін регрессияның ең кіші квадраттық тәсілі қолданылады
болсын. Z кеңістігінің ауыспалы проекциясының эндогені - у
i
(оны шығару үшін регрессияның ең кіші квадраттық тәсілі қолданылады
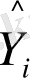 =
a
i
+
=
a
i
+
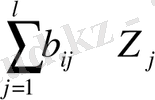 ) . Ауыспалы
) . Ауыспалы
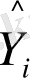 сызықтық комбинациялы инструментальды ауыспалы, олар у
i
ауыспалысымен тығыз корреляцияланады.
сызықтық комбинациялы инструментальды ауыспалы, олар у
i
ауыспалысымен тығыз корреляцияланады.
Кейде эндогенді айнымалылардан «тазарту» деп структуралық форма жүйесінде Ү
i
-дан
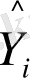 -ға ауысуын айтамыз. Осы жағдайда қатемен корреляцияланатын регрессия алынып тасталынады.
-ға ауысуын айтамыз. Осы жағдайда қатемен корреляцияланатын регрессия алынып тасталынады.
Z 1 және Z 2 инструментальды айнымалы моделін мысал ретінде қарастырып көрейік.
Y
1
=
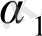 +
+
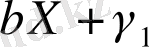 Y
2
+
Y
2
+
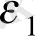 ;
;
Y
2
=
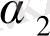 +
+
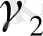 Y
1
+
Y
1
+
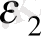 ;
;
Уақытша бағаналарға қатысты 9. 2 суретінде графикалық бейне көрсетілген.
Моделге қарапайым ең кіші квадраттық тәсілді қолдана отырып, келесі бағалауды аламыз
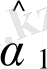 =4, 837;
=4, 837;
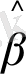 =0, 263;
=0, 263;
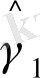 =0, 206; (11. 17)
=0, 206; (11. 17)
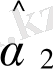 =1, 116;
=1, 116;
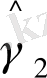 =0, 385
=0, 385
Енді инструментальды айнымалылар ретінде X, Z 1 , Z 2 -ні алып, инструментальды айнымалылар тәсілін қолданамыз. Бұдан алынған бағалаулар мына түрге ие:
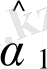 =3, 632;
=3, 632;
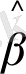 =0, 241;
=0, 241;
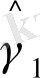 =0, 522; (11. 17´)
=0, 522; (11. 17´)
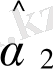 =-1, 783;
=-1, 783;
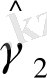 =0, 675
=0, 675
және (11. 17) бағалауларына қарағанда, бұл бағалаулардың айырмашылығы бар. Ең кіші квадраттық екіөлшемді тәсіл арқылы жақсы нәтиже бағаларын алуға болады. Олар мына түрді береді:
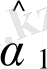 =3, 632;
=3, 632;
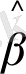 =0, 241;
=0, 241;
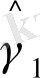 =0, 522;
=0, 522;
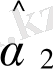 =-1, 783;
=-1, 783;
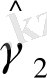 =0, 675.
=0, 675.
Бірқалыпты регрессионды теңдеуді бағалау. Сырттай байланыспаған теңдеулер
Формада жекеше түрде келтірілген теңдеу ең кіші квадраттық жанама тәсіл негізінде бағалауға қосылады.
Ү
1
=
a
1
+b
1
x
1
+
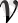 1
(11. 18)
1
(11. 18)
Y
2
=
a
2
+b
1
x
2
+
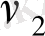 (11. 19)
(11. 19)
Бұдан, жалпы айтқанда, cov(
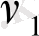 ,
,
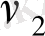 )
)
 0. Ең кіші квадраттық жалпылама тәсілін қолданса және (11. 18), (11. 19) теңдеуін біріктірсе, онда бағалаудың тиімділігін жоғарылатуға болады.
0. Ең кіші квадраттық жалпылама тәсілін қолданса және (11. 18), (11. 19) теңдеуін біріктірсе, онда бағалаудың тиімділігін жоғарылатуға болады.
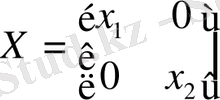
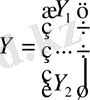
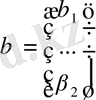
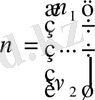 .
.
Онда (11. 18) -(11. 19) теңдеуін мына түрде жазуға болады:
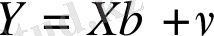 (11. 20)
(11. 20)
∑
11
=Cov(
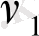 ,
,
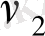 ), ∑
12
= Cov(
), ∑
12
= Cov(
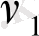 ,
,
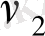 ), ∑
22
= Cov(
), ∑
22
= Cov(
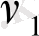 ,
,
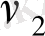 ) . (11. 21)
) . (11. 21)
 ∑
ij
матрицасы - скалярлы егер классикалық модель шартын (11. 18), (11. 19) теңдеуі жекеше түрде қанағаттандырса. Онда
∑
ij
матрицасы - скалярлы егер классикалық модель шартын (11. 18), (11. 19) теңдеуі жекеше түрде қанағаттандырса. Онда

қателік регрессия (11. 20) теңдеуінің ковариациялық матрицасы бар. Ең кіші квадраттық (11. 20) теңдеудің жалпыланған тәсіл бағалауы мынадай түрге ие:
b * =(x 1 ∑ -1 x) -1 x 1 ∑Y.
Практикалық қолдануға ең кіші квадраттық жалпыланған тәсілдің ∑ матрицасын бағалау керек.
 (e
i
, e
j
) таңдамалы ковариация, ∑
ij
матрицаны бағалау ретінде қабылдау және регрессия қалдығын табу арқылы жекеше түрде (11. 18), (11. 19) теңдеуін бірінші ең кіші квадраттық тәсілді қолдану арқылы орындауға болады.
(e
i
, e
j
) таңдамалы ковариация, ∑
ij
матрицаны бағалау ретінде қабылдау және регрессия қалдығын табу арқылы жекеше түрде (11. 18), (11. 19) теңдеуін бірінші ең кіші квадраттық тәсілді қолдану арқылы орындауға болады.
Ең кіші квадраттық жанама тәсіл әсерін бірқалыпты бағалау тәсілін қолдана отырып жоғарылатуға болады. Теңдеуге жекеше түрде қолданылған ең кіші квадраттық тәсіл бағалауымен сәйкес келеді, егер екі теңдеуде де экзогенді айнымалылар жиынтығы сәйкес келсе. Стандарттты компьютерлік дестелерде регрессионды теңдеу жүйесінің бірқалыпты бағалау процедурасы сырттай байланыспай іске асырылады. Seemingly Unreleased Regression (SUR) деп бағалау тәсіліне сәйкес эконометрикалық дестелерде айтылады.
8 тараудан мысал қарастырайық. Онда модель түрі қарастырылған болатын
Ү=
 +
+
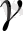 x+
x+
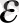 , (2. 22)
, (2. 22)
бұндағы Ү- соңғы өнім бағасы, Х- жартылай дайын өнімнің құны.
Инструментальды айнымалы тәсілін қолдана отырып, келесі теңдеуді аламыз:
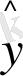 =16, 72+1, 408x (11. 23)
=16, 72+1, 408x (11. 23)
Бұл тарауда біз регрессионды теңдеу жүйесін құру арқылы модельді қиындатып аламыз. Х жартылай дайын өнімнің бағасы шикізаттың жалпы санының бағасына тәуелді, яғни W=Z 1 +Z 2 бағасына Z-жалпылама фактор өндірісінің соңғы өнімі. Модель түрін қарастырайық
X=
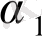 +
+
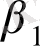 W+
W+
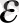 1
,
1
,
Y=
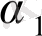 +
+
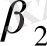 Z+
Z+
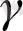 X+
X+
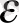 2
(11. 24)
2
(11. 24)
Бұдан
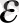 1
,
1
,
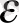 2
коррелирланады, сондықтан х-эндогенді айнымалы. (11. 24) жүйеде келтірілген форма мына түрге ие:
2
коррелирланады, сондықтан х-эндогенді айнымалы. (11. 24) жүйеде келтірілген форма мына түрге ие:
X=
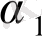 +
+
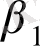 W+
W+
 1
,
1
,
Y=(
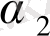 +
+
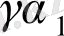 ) +
) +
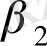 Z+
Z+
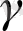
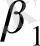 W+(
W+(
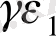 +
+
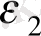 ) (11. 25)
) (11. 25)
Келесі бағалаулар мәнін ең кіші квадраттық жанама тәсіл береді:
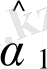 =19, 31;
=19, 31;
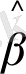 1
=1, 77;
1
=1, 77;
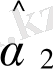 =18, 0;
=18, 0;
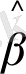 2
=0, 55; (11. 26)
2
=0, 55; (11. 26)
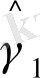 =1, 325.
=1, 325.
Енді сырттай байланыспаған бірқалыпты (11. 25) теңдеуін бағалайық. Нәтижесінде мынадай теңдеу шығады:
 =19, 31+1, 77W, d=1, 9, R
2
=0, 984;
=19, 31+1, 77W, d=1, 9, R
2
=0, 984;
(6, 98) (0, 03)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz