Жазықтықтағы фигуралардың кесілуі

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Жоспар

Жазықтықтағы фигуралардың кесілуі
Коэн-Сазерленд кесу алгоритмі
Кеңістікті кодтау
Тік бұрыш ауданы бойынша қиындыны қию
Тікбұрышты аудан бойынша кесу алгоритмі. Кируса-Бек алгоритмі

Жазықтықтағы фигуралардың кесілуі

Жазық сцена және реттелген форманың қиылысатын терезесі көрсетілген. Терезе сол (с), оң (о), жоғарғы (ж), төменгі (т) екі өлшемді қабырғамен беріледі. Реттелген қиылысқан терезелер тіктөртбүрыштар болады. Олар объектіні кеңістіктің координат объектілеріне параллель немесе экран координат осьтеріне параллель. Немесе экран координат осіне қиылысу алгоритмінің мақсаты қиылысатын терезенің ішінде жатқан нүктелер, қиындылар визуализация үшін қалдырылады.

Қарапайым сценалар немесе картинкада нүктенің көп санын қию керек болса, онда көпжағдайда қиылысу алгоритмін тиімді нүктелер толық ішінде жатады. Сондықтан қиындыларды тез алу керек.

Қиылысатын терезенің ішінде жататын нүктелер келесі шартты қанағаттандырады.

Теңдік белгісі терезе шекарасында жатқан барлық нүктелер оның ішінде х _л <= х <= х _п и у _н <= у <= у _в . деп саналады

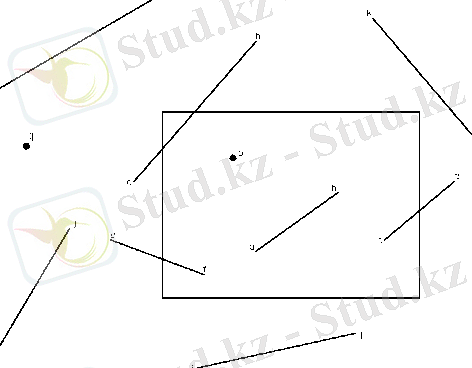
Теңдік белгісі көрсетеді. Мүнда терезе шегінде нүктелер оның ішінде орналасқан деп саналады. Қиынды терезе ішінде жатыр.

Сондықтан ол көрінеді. Егер оның соңғы нүктелері терезе ішінде жатса, мысалы суретте ab қиындысы. Бірақ қиындының екі соңында терезеге жатпаса, онда бүл қиынды терезеден тысжатуы міндетті емес, мысалы gh қиындысы.

Коэн-Сазерленд кесу алгоритмі

Шығару өрісіне қиындыны жатқызуды анықтау есебін шешу үшін келесі эдіс қолданылады. Кеңістік 9 ауданға бөлінеді, эр аудан бинарлы 4 битті.

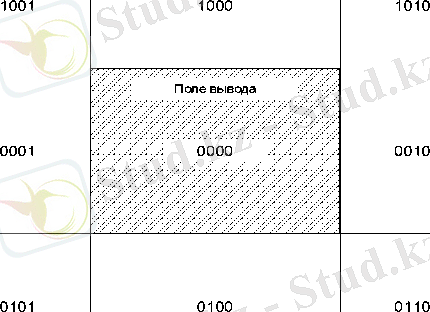
Кеңістікті кодтау

Әр қиынды үшін код соңы есептеледі. Содан кейін талдау экспрет жүргізіледі.

Егер К ₁ Л К ₂ #0, онда қиынды шығару өрісінде жатқан жоқ - қиынды тасталады.

Егер К ₁ =К ₂ =0, онда қиынды толығымен шығару өрісінде жатыр - қиылысу керек емес, қиынды толық суреттеледі.

Егер К ₁ Л К ₂ =0 қиынды бөліктеп шығару өрісінде жатуы мүмкін - шығару өрісі не қиылысу қажет.

Тік бұрышты аудан бойынша қиылысу алгоритмі

Егер К ₁ Л К ₂ =0 қиындыны шығару өрісі шекарасымен қию керек, қиылысу суреттің барлық жағынан жүреді.

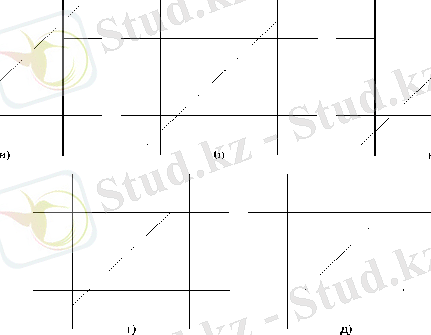
Тік бұрыш ауданы бойынша қиындыны қию

қиылысу жүретін қабырға бөлінген. Шығару өрісі шекарасында жатқан нүктелер шығару өрісіне жатады.

Тікбұрышты аудан бойынша кесу алгоритмі. Кируса-Бек алгоритмі

Қиюдың сенімді алгоритмін қүру үшін кесіндіге жататын нүктенің терезеге (ішінде, шекарасында немесе одан тыс) қатынасты орналасуын анықтайтын жақсы тәсіл болуы керек. Бүл мақсат үшін Кируса-Бек алгоритмінде вектор нормалі пайдаланылады.

R қиылатын выпукл аймағын алайық. R-дің екі өлшемді болуы міндетті емес, берілген бөлімде келтірілетін мысалдарда, ол екі өлшемді. Яғни, R кез келген выпукл жазық көпбүрыш болуы мүмкін. Ол вогнут көпбүрыш болмауы керек. Ерікті а нүктесіндегі R-дің шекарасында жатқан п ішкі нормалі п-(Ь- а) ^ 0 шартын қанағаттандырады, мұндағы b - R шекарасындағы кез келген басқа нүкте. Бүгін убедиться, еске алайық, V ₁ және V ₂ екі сколярлық вектордың көбейтіндісі V ₁ V ₂ *[V ₁ ] [V ₂ ] соң-кетең, мұндағы Q - V ₁ және Ғ ₂ -ден жасалған екі бүрыштың кішісі. Байқайық, егер Ө = к 12, болса, онда cos Ө =0 және V ₁ * V ₂ =0, яғни жүп векторлардың сколярлық көбейтінділері нөлге тең болғанда олар перпендикуляр. 10. 4 суретте R выпукл аймағы көрсетілген, яғни қиятын терезе. Сол жерде ішкі (сыртқы) п _н жэне а нүктесінен шығатын сол шекарада жатқан терезенің шекарасына нормальдың ішкі п _в көрсетілген.

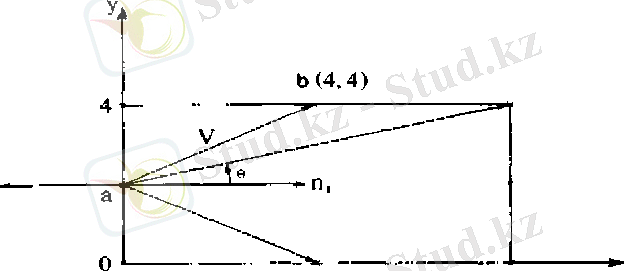
Одан басқа а нүктесінен, терезе шекарасының басқа нүктелеріне жүргізілген бірнеше векторлар көрсетілген. п _в -мен кез келген осындай векторлар арасындағы бүрыш -к/2 <Ө<к/2 интервалына жатады. Бүрыштың мұндай мәндерінде оның косинусы әр уақытта оң. Сондықтан, жоғарыда тағайындалғандай бүл векторлардың сколярлық көбейтіндісі оң. Ал сыртқы нормальдар арасындағы бүрышпен жэне сол сияқты кез келген векторлар тең к - Ө, а cos (к - Ө) = - Ө бүл жағдайда теріс.

Анықтамаға қайта келсек, терезенің жағымен кесіндінің қиылысуы қайтадан Р] Р ₂ кесінділерінің параметрлік көрсетілуін аламыз:

P(t) = Р1 + (Р2 - 0 < t < 1.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.