Инженерлік графика және сызба геометрия: Монж әдісі, ортогональды проекциялар және позициялық-метрикалық есептер


1. Инженерлік графика нені зерттейді және оның негізгі мақсаттары
Қазіргі кезде инженерлік графика пəні сызба геометрия пəні мен машина жасау жəне құрылыс сызбаларының теорияларын зерттейтін ғылым. Инженерлік графика теорияларының жетістіктері техника мен ғылымның əртүрлі салаларында кеңінен қолданылуда. Сондықтан жер жұмыстарының сызбаларын сауатты орындау, инженерлік ғимараттарды жобалау жəне тұрғызу үшін, жер бетінде салынатын ғимараттарды сызбада кескіндеу теориясының негіздерін инженер осы инженерлік графика теориясы арқылы біліп, үйренеді.
Сызықтық геометрия- кеңістіктегі фигуралар, олардың шешу әдістері және кеңістіктік есептерді жазықтықтағы суреттермен зерттейтін геометрияның бөлігі. Сызықты геометрияның әдістері техникалық сызудың теориялық базасы болып табылады. Бұл ғылымның мақсаты - машинасалу, архитектура және құрылыс объектілерінің пішінін салу, объектілер мен процестердің графикалық кескінін өңдеу.
Сызықтық геометрияды:
- Кеңістіктегі фигураларды жазықтықта салудың әдістері;
- Геометриялық есептердің графикалық және аналитикалық шешуінің әр түрлі әдістері;
- Салынған объектінің геометриялық қасиеттерін зерттеу және түрлендіру әдістері;
- Геометриялық объектілердің моделдеу зерттеледі
Сызу геометрияда салынған суреттер предметтердің ойдағы формасын елестетуге мүмкіндік беріп, кеңістіктік елестетуді дамытады. Сызу геометриядағы сызуларды салу әдісінің ережелері проекциялық әдіске негізделген. Проекциялық әдісте ең алдымен нүктенің проекциясын салу қарастырылады. Себебі кез келген кеңістіктік фигураларды салу осы фигура бойында жататын нүктелердің жиынтығы ретінде қарастырылады.
2. Монж әдісі, Проекциялық жазықтықтар
Егер нүкте мен проекция жазықтығының арақашықтығы туралы ақпаратты сандық белгілеу көмегімен емес екінші проекциялар жазықтығында тұрғызылған нүктенің проекциясы арқылы берсе, онда сызба екі көріністі немесе кешенді деп аталады. Осындай сызбаның негізгі принциптерін француз ғалымы Гаспар Монж (1746-1818) келтірген.
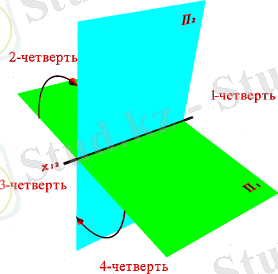
Г. Монждің ұсынған әдісі бойынша кеңістікте екі өзара перпендикуляр орналасқан проекция жазықтықтарын қарастырамыз. Жазықтықтардың біреуін деп белгілейміз және горизонталь
орналастырамыз, ал екінші жазықтығын вертикальды орналастырамыз. - горизонтальды, - фронтальды проекциялар жазықтығы.
Проекция жазықтықтары кеңістікті төрт екі жақты бұрыштарға - төрт ширекті кеңістіктерге бөледі.
Ортогональды проекцияларға байланысты, проекция жазықтықтарынан бақылаушы шексіз үлкен қашықтықта бірінші ширекте тұр деп есептейміз. Проекция жазытықтарының қиылысу түзуі координатлар өсі деп аталады 2 немесе болып белгіленеді . Көрсетілген проекциялардан тұратын жазық сызба алу үшін П 1 жазықтығын x 12 өсімен айналдыру арқылы П 2 жазықтығымен беттестіреміз. Нәтижесінде алынған сызба Монж Эпюрі деп аталады. Геометриялық объектілер сызықты (нүкте, түзу, жазықтық), сызықты емес(қисық сызық, бет) және құраушы (көпжақтар) болып бөлінеді. Монж ұcынған тәсіл. Есiмi тарих бетiнде қалған Госпар Монж (1746-1818) көрнектi француз геометрi, XVII ғасыр аяғында және Напалеон I басшылық еткен 1789-1794 жылдар аралығындағы қоғамдық және мемлекеттiк қайраткер. Париждегi белгiлi Политехникалық мектептiң негiзiн қалаушы. Өлшем мен салмақтың метрлiк жүйесiн енгізу жұмысын жүргiзуге қатысқан. Франциядағы революция кезiнде министрлiк қызмет атқарған.
Монж әдiсiнiң үлкен құпия мәнi болғандықтан, еңбегiн жариялауға тиым салынады. Тек XVIII ғасырдың аяғында ғана басылуға мүмкіндік берiлдi.
Кеңiстiктегi пiшiндi жазықтықта бейнелеу қажеттiгi ежелгi заманнан берi жинақталып келдi. Техниканың дамуына байланысты алғашқы мәнi өлшеуге жеңiл нақты бейнелермен қамтамасыз ететiн қандайда бiр тәciлдiң
қажеттiгiн туғызады. Ол нүктенiң бейнедегi басқа үктелерге қарағанда орнын дәл анықтау, фигуралар мен түзукесiндiлерiнiң өлшемдерiн табу мүмкiндiгiнiң жеңiл жолдары. Француз ғалымы Монж бiртiндеп жинаған
әртүрлi ережелермен бейнелердi салу тәсiлдерiн бiр жүйеге келтiрiп, 1799 жылы «Geometrie dtscrihtive» деп аталатын еңбегiн басып шығарады.
Ортогональды проекцияда кеңicтiктегi геометриялық
фигуралардың пiшiнi мен орнын анықтауға ең қолайлысы өзара перпендикуляр болатын үш жазықтықтан тұратын декартты жүйе болып табылады. Геометриялық фигуралардың ортогональды проекцияларын салғанда
кеңicтiктегi макеттi қолдану өте ынғайсыз, көрнектi емес. Сондықтан бейне ретiнде сызбада кеңicтiктегi макеттiн орнына - эпюр сызбасы қолданылады, ол екi немесе үш өзара байланысқан геометриялық фигуралардың
ортогональды проекцияларынан тұрады. Монж көрнектi түрде проекция жазықтықтарын, олардың жалпы
жазықтықта беттесетiндей етiп қиылысу сызығымен қалай айналдыру керектiгiн көрcеттi. Бұнда ол бейнеленетiн заттың өзiн алып тастап, тек оның бейнелерiн, яғни проекцияларын қалдырған. Бұндай сызу комплекстi немесе Монж эпюрi деп аталады
Проекциялық жазықтықтар
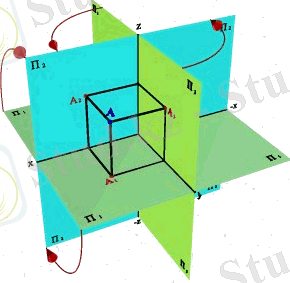
Бұл жазықтықтағы нүктелердің проекциялары үлкен әріптермен немесе 3 индексті сандармен белгіленеді.
Проекциялар жазықтығы жұп-жұбымен қиылысып Ox , Oy және Oz үш өсін анықтайды. Оны кеңістіктегі О нүктесімен басталатын декарттық координаттар жүйесінде қарастыруға болады. Үш проекциялар жазықтығында нүктенің эпюрін салу үшін П 1 және П 3 проекциялар жазықтықтарын 2. 4. - суреттегідей П 2 жазықтына айналдыру арқылы беттестіреміз. Кеңістіктегі немесе беттегі нүктенің орналасу жағдайын анықтау үшін сандардан тұратын координаттарды береміз. Үш өлшемді кеңістікте нүктенің орналасу жағдайын тік бұрышты декарттық координаттар x , y және z көмегімен анықтайды(абсцисса, ордината және аппликата) .
Егер нүкте жазықтықтардың біреуінде жататын болса, проекциялар жазықтығына қарағанда нүкте жеке жағдайдағы нүкте деп аталады. Егер нүкте ешқандай жазықтықта жатпайтын болса, онда нүкте жалпы жағдайдағы нүкте деп аталады.
3. Ортогональді проекциялау Сандық өлшеулері бар проекциялар
Ортогональды проекция ( сызба геометрияда ) - кеңістіктегі нысанды жазықтықта проекциялау жазықтығына перпендикуляр проекциялық сәулелер арқылы бейнелеу. Техникада кеңінен қолданылады. Топографиялық карталар мен пландарды жасауда ортогональды проекцияда жүргізіледі, осының өзінде карта парағының шегіндегі деңгейлік бет жазықтық ретінде, ал тік сызықтар оған перпендикуляр болып қабылданады. Топографиялық картаға (планға) жергілікті жердегі өлшенген еңістік қашықтықтар емес, олардың горизонталь ізбелері түсіріледі, демек, 1:100 000 не одан ірірек масштабты топографиялық картаның (планның) жеке парағы - онда бейнеленген жер бетінің ортогональды проекциясы болып табылады. Ортогональды проекция негізгі екі қасиетімен (графикалық құрылымдардың дәлдігі шегінде) сипатталады: 1) картадағы (пландағы) қашықтықтар жергілікті жердегі тиісті қашықтықтардың горизонталь ізбелеріне пропорционал және 2) ұшы картаның (планның) кез келген нүктесіндегі бұрыштар жергілікті жердегі тиісті горизонталь бұрыштармен тең. [1
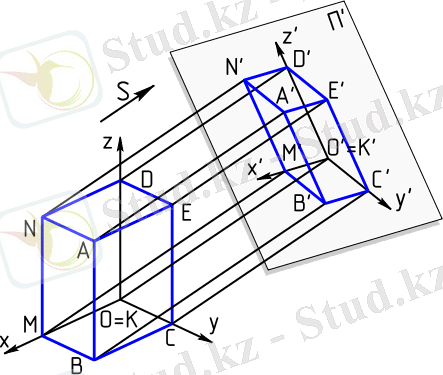
Сандық өлшеулері бар проекциялар
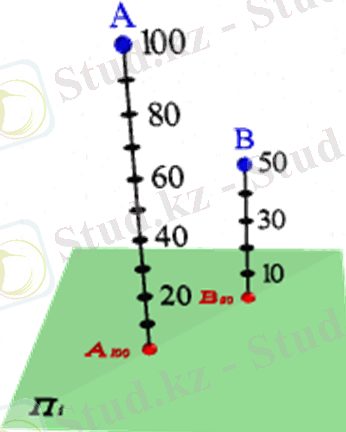 Сандық белгілеулері бар проекцияларда
П
i
проекция жазықтығын нөлдік деңгейдегі жазықтық деп атайды және
П
0
деп атайды.
Сандық белгілеулері бар проекцияларда
П
i
проекция жазықтығын нөлдік деңгейдегі жазықтық деп атайды және
П
0
деп атайды.
Бүл әдістің мәні мынада: П 0 жазықтығына нүктені ортагональды проекциялайды және сонымен қатар нүкте проекциясынан оның П 0 жазықтығына дейінгі қашықтығын белгілейді, Бұл арақашықтықты сандық белгілеу деп атайды және әдетте оны метрмен өлшейді,
4. Октанттар . Екі проекциялық жазықтықтағы нүктенің ортогональді проекциясы
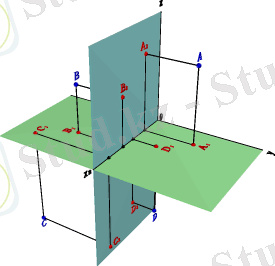
Егер өзара тікше (перпендикуляр) орналасқан екі проекция жазықтықтарына үшінші проекция жазықтығын перпендикуляр орналастырсақ, онда бұл үш проекция жазықтығы үшөлшемді кеңістікті сегіз бөлікке бөледі. Бұл бөлінген бөліктерді октанттар деп атап, рим сандарымен белгілейді (6-сурет) . Октант ежелгі гректің сегіз деген сөзі. Үшінші проекция жазықтығын қаптал (профиль) жазықтығы дейді. Қаптал жазықтығын П3 əрпімен белгілейміз. 6-суретте бұл жазықтық жасыл түспен боялған. Бұл жазықтық алғашқы екі жазықтықпен екі қиылысу сызығымен қиылысады. П1 жəне П3 проекция жазықтықтарында бұл қиылысу түзуі ордината осі болады. Ал, П2 жəне П 3 проекция жазықтықтары өзара қиылысып, аппликата осін береді.
Егер қаптал жəне қарама-қарсы проекция жазықтарын 6-суретте көр- сетілгендей етіп бұрып, өзара беттестірсек, онда беттескен бір ғана проекция жазықтығын аламыз (7-сурет) . Енді кеңістікте орналасқан нəрсенің жазық кескінін алу үшін, осы беттескен бір ғана жазықтық сызбасын саламыз. Бұл жазық кескінді эпюр немесе сызба деп атайды. Эпюрде кеңістікте орналасқан А мен В нүктелерінің эпюрлері мен П1 проекция жазықтығының бойында жатқан С нүктесінің эпюрі көрсетілген. Мысалы, 7-суретте горизонталь проекция жазықтығы қоңыр түспен, фронталь проекция жазықтығы сары түспен жəне профиль проекция жазықтығы жасыл түспен берілген. Егер нүктенің горизонталь проекциясы А1 қоңыр түсті жазықтықта, фронталь проекциясы А2 сары түсті жазықтықта, ал профиль проекциясы А3 жасыл түсті жазықтықта орналасса, онда бұл нүкте - бірінші ширектенемесе бірінші октантта орналасқан нүкте болғаны (себебі бұл нүктенің координаталардағы таңбалары оң болғаны) (7-сурет) . Егер осы заңдылық бұзылса, онда ол нүктенің таңбаларының біреуі немесе екеуі теріс таңбалы болғаны. Төменде 1-кестеде октанттардағы орналасқан нүктелердің координаталық таңбалары көрсетілген. Осы таңбаларға қарап, нүктенің қай октантта орналасқанын жеңіл анықтай аламыз.
нүкте екі проекция жазықтықтарының ортогональды жүйесінде
Жазықтыққа түсірілген нүктенің ортогональды проекциясы берілген нүктеден осы жазықтыққа түсірілген перпендикулярдың табаны деп аталады. 2. 1. - Суретте А нүктесі және оның екі А 1 және А 2 ортогональды проекциялары көрсетілген.
А 1 нүктесін А нүктесінің горизонтальды проекциясы, А 2 нүктесін фронтальды проекциясы деп атайды. Нүкте проекциялары 2 орналасқан және осы өсті А нүктесінде қиып өтеді.
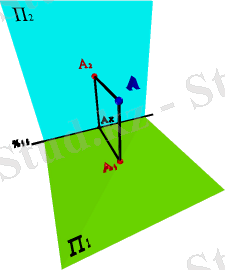
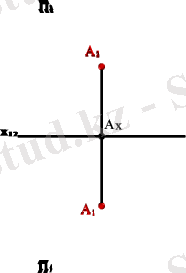
Монж эпюрінде А 1 және А 2 проекциялары 2 өсіне перпендикуляр түзуінде орналасқан . Нүктелердің горизонтальды проекцияларынан оске дейінгі А 1 А x - арақашықтығы А нүктесімен П 2 жазықтығына дейінгі қашықтыққа тең.
Эпюрде нүкте проекцияларын қосатын түзу сызықтар проекциялар байланысының сызығы деп аталады.
2. 2. - Сурет. Кеңістіктің әртүрлі ширектерінде орналасқан нүктелер
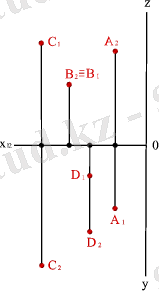
5. Позициялық және метрикалық есептер
Позициялық(тұрғылықты) жəне метрикалық (өлшем) есептер жалпы сызба геометрияның негізгі есептері болып табылады. Позициялық (тұрғылықты) есептер дегеніміз - геометриялық фигуралардың сызбалары арқылы олардың кеңістіктегі өзара орналасуын анықтайтын есептер. Позициялық есептерге: нүкте мен түзудің, түзу мен түзудің, нүкте мен жазықтықтың, түзу мен жазықтықтың, жазықтық пен жазықтықтықтың, жазықтық пен беттің, екі беттің өзара орналасу есептері жатады. Метрикалық (өлшем) есептер дегеніміз - геометриялық фигуралардың сызбалары арқылы олардың кеңістіктегі өзара қашықтықтарын, олардың арасындағы бұрышын жəне олардың ауданын, нақты шамасын т. с. с. жағдайын анықтайтын есептер.
4. 1 Позициялық есептер
Күрделі емес позициялық есептерді шешуде көбінесе жалпы əдістер пайдаланылады. Бұл параграфта кеңістіктегі нүкте мен түзу сызықтың өзара орналасуы, кеңістіктегі түзу сызықтардың өзара орналасуы, кеңістіктегі екі жазықтықтың өзара орналасуы жəне кеңістіктегі түзу мен жазықтықтың өзара орналасулары сияқты позициялық есептерді қарастырамыз.
4. 1. 1 Нүкте мен түзу сызықтың өзара орналасулары
Кеңістікте нүкте мен түзу сызық əртүрлі жағдайда кездесуі мүмкін. Кеңіс- тікте нүкте түзу сызық бойында немесе түзу сызықтан тыс орналасуы мүмкін. Осы тақырыпқа мысал ретінде 36-суреттегі нүктелер мен түзудің өзара орналасуларын қарастырайық. 36-суреттегі С5 нүктесі - А5В2 түзу сызығынан тыс жатқан нүкте. Ал, D3 нүктесі - А5В2 түзу сызығының бойында жатқан нүкте, өйткені бұл нүкте түзу сызықтың ен аралыққа бөлгендегі үшінші бөлігіне тең.
4. 1. 2 Түзу сызықтардың өзара орналасулары
Түзу сызықтар кеңістікте өзара орналасуларына байланысты: параллель, қиылысқан, айқасқан жəне перпендикуляр (тікше) болып келеді. Егер кеңістіктегі екі түзу сызықтың көлд енең П0 проекция жазықтығындағы кескіндерінің кескін табандары өзара параллель, ен аралықтары тең жəне сан- дық белгілері бір бағытта өсетін болса, онда мұндай түзу сызықтарды өзара парал лель түзулер дейді.
4. 1. 3 Екі жазықтықтың өзара орналасуы
Жазықтықтар да түзу сызықтар сияқты өзара параллель жəне қиылысқан болып келеді. Егер кеңістікте орналасқан екі жазықтықтардың көлбеу масштабы арқылы берілген проекциялары өзара параллель, ен аралықтары тең жəне сандық белгілері бір бағытта өссе (немесе төмендесе), онда мұндай жазықтықтарды өзара параллель жазықтықтар деп атайды.
4. 1. 4 Түзу мен жазықтықтың өзара орналасулары
Кеңістікте түзу сызықтар жазықтыққа параллель, меншікті (жазықтық бойында жатады) жəне перпендикуляр (тікше) қиылысады. Енді осы жағдайларға мысал қарастырамыз. Егер түзудің екі нүктесі жазықтық бойында жатса, онда мұндай түзу сызық жазықтыққа меншікті болады. Мысал қарастырайық. 44-суретте Р жазықтығының көлбеу масштабы арқылы берілген кескіні көрсетілген. Түзудің А жəне В нүктелері осы жазықтықтың аттас горизонтальдарының бойында жатыр, яғни АВ түзу сызығы Р жазықтығына меншікті болады.
4. 2 Метрикалық есептер
Сандық белгісі бар проекциялар горизонталь П0 жазықтығында орындалса да, сызбада тікбұрышты (ортогональ) проекциялар қағидаларымен құрылатын болғандықтан, тікбұрышты проекцияларда қолданылатын əдістердің көбін сандық белгісі бар проекцияларда да пайдалануға болатынын айта кету керек. Сондықтан метрикалық (өлшем) есептерді шешуде жалпы əдістерді пайдаланамыз.
4. 2. 1 Түзу сызықтың нақты шамасы мен жазықтыққа жасайтын бұрышы
Егер түзу сызық кеңістікте жалпы жағ дайда орналасқан болса, онда оның көлденең П0 жазықтығындағы проекциясы бұрмаланып, түзу сызық ұзын немесе қысқа болып кескінделеді. Сандық белгісі бар проекцияларда жалпы жағдайда берілген түзу сызықтың нақты шама сын (ұзындығын) табу үшін, берілген А4В6 түзуінің А4 жəне В6 нүктелерінен түзуге перпендикуляр сызық жүргіземіз. Осы сызық бойына сан өлшемдерін өлшеп саламыз. Егер табылған А жəне В нүктелерін өзара қоссақ, онда жүргізілген түзу сызық ұзындығы түзудің нақты шамасы болады (48-сурет) .
4. 2. 2 Нүкте мен жазықтықтың арақашықтығы Жоғарыда айтып кеткендей, метрикалық есептер деп гео метриялық фигуралардың сыз бал ары арқылы олар дың кеңіс тік тегі өзара қашық тықтарын анық тайтын есептерді айтады.
7. Түзусызық. Түзусызықтың графикалық берілу әдісі. Проекция жазықтығына қатысты түзу сызықтың орналасуы
Түзу сызық дегеніміз - бір түзу бойындағы нүктелер жиынтығы. Мектеп бағдарламасында геометрия пəнінен өткендей, бір нүктеден басталып сызылған түзуді
сəуле
дейміз. Ал екі нүктеден өткен түзуді
кесінді
дейміз. Сызба геометрияда түзу сызықтар нүктелер жиынтығы болғандықтан, түзу
Түзу сызық. Түзудің графикалық бейнелену түрлері.
Түзу сызық геометрияның негізгі түсініктерінің бірі болып табылады. Егер геометрияны тұрғызу негізінде кеңістіктегі екі нүктенің арақашықтық түсінігі қарастырылатын болса, онда түзуді екі нүктенің ең кіші арақашықтығы ретінде қарастыруға болады.
Түзу сызық сызықты алгебрада бірінші ретті сызық болып табылады. Түзудің жалпы теңдеуі:
А х+ В у+ С =0,
А, В және С - кез-келген тұрақтылар.
Проекция жазықтықтарына қатысты түзудің орналасуына байланысты жеке немесе жалпы жағдайларын қарастыруға болады.
1. Проекция жазықтықтарының ешбіріне параллель емес түзу жалпы жағдайдағы түзу деп аталады (3. 4. - сурет) .
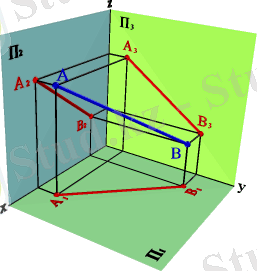
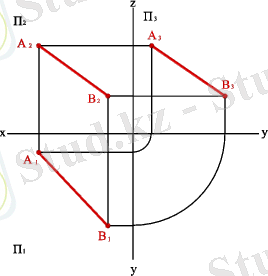 3. 4. -Сурет. Жалпы жағдайдағы түзу
3. 4. -Сурет. Жалпы жағдайдағы түзу
2. Проекция жазықтықтарына параллель түзулерді жеке жағдайдағы түзулер ретінде қарастыруға болады және оларды деңгейлік түзулер деп атайды. Берілген түзуді қай жазықтыққа параллель екеніне байланысты ажыратады:
2. 1. Горизонтальды проекция жазықтығына параллель түзу горизонталь түзу немесе горизонталь деп аталады (3. 5. - сурет) . Кез-келген горизонталь нүктелер жұбына мына теңдеу сәйкес келеді:
z A =z B ⇒ A 2 B 2 //Ox; A 3 B 3 //Oy ⇒
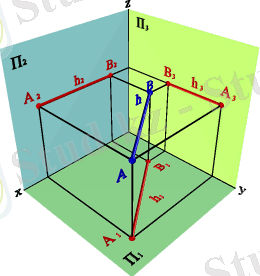
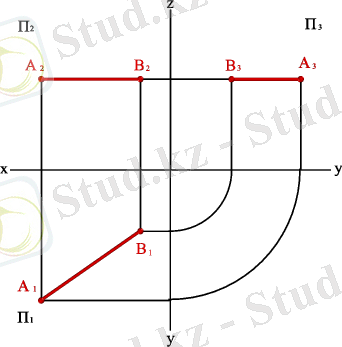 3. 5. - Сурет. Горизонталь түзу
3. 5. - Сурет. Горизонталь түзу
2. 2. Фронталь проекциялар жазықтығына параллель түзулер фронталь деп аталады (3. 6. - сурет) .
⇒ Α 1 OO⇒
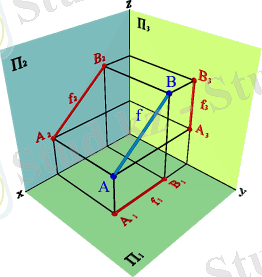
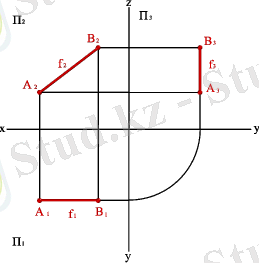 3. 6. - Сурет. Фронталь түзу
3. 6. - Сурет. Фронталь түзу
2. 3. Профилді проекция жазықтығына параллель түзу профиаль деп аталады (3. 7. - сурет) .
xx⇒ Α 1 Β 1 //Oy, O⇒
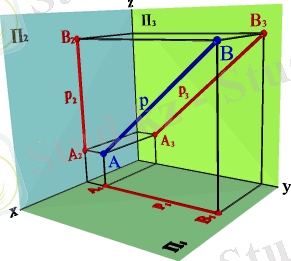
Түзу сызықтың өзара орналасуы.
Түзу сызықтар кеңістікте параллель, қиылысатын
және айқас болуы мүмкін.
1. Параллель түзулер .
Бір жазықтықта жататын және ортақ нүктелері жоқ екі түзу параллель түзулер деп аталады.
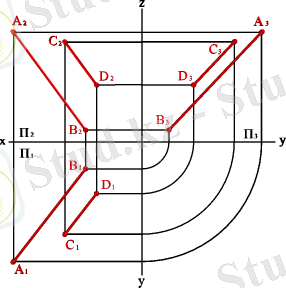 3. 19. - Сурет. Параллель түзулер
3. 19. - Сурет. Параллель түзулер
Параллель түзулердің кез-келген жазықтықтағы проекциялары параллель болады.
Параллель проекциялардың бұл қасиеті ортогональды проекциялар үшін де қолданылады, егер AB//CD онда A 1 B 1 // C 1 D 1 ; A 2 B 2 // C 2 D 2 ; A 3 B 3 // C 3 D 3 (3. 19 сурет) .
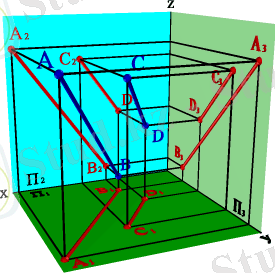
Жазықтықтардың біріне параллель түзу ерекше жағдайды ұстанады. Мысалы, профиль түзудің фронталь және горизонталь проекциялары параллель, бірақ олардың өзара орналасуын анықтау үшін профиль проекциялар жазықтығында түзулердің проекцияларын салу қажет. (3. 20. - сурет) . Қарастырып отырған жағдайда кесінділердің П 3 жазықтығындағы проекциялары қиылысады, демек шығатын қорытынды, олар параллель емес.
Бұл сұрақтың шешімін екі қатынасты салыстыру арқылы аламыз:
А 2 В 2 / А 1 В 1 = С 2 Д 2 / С 1 Д 1 ⇒ АВ//СД
А 2 В 2 / А 1 В 1 ≠ С 2 Д 2 / С 1 Д 1 ⇒ АВ//СД
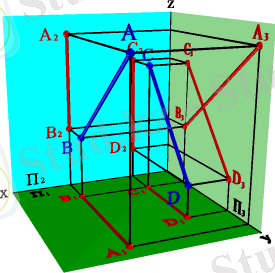
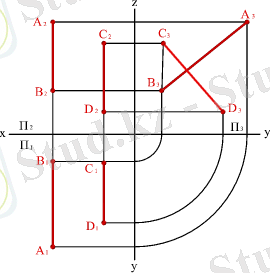 3. 20. -Сурет. Профиль проекциялар жазықтығына параллель түзулер.
3. 20. -Сурет. Профиль проекциялар жазықтығына параллель түзулер.
2. Қиылысатын түзулер.
Бір жазықтықта жататын ортақ нүктелері бар екі түзу қилысушы түзулер деп аталады. Егер түзулер қиылысатын болса, онда олардың аттас проекцияларының қиылысу нүктелері бір байланыс сызығының бойында жатады. (3. 21. - сурет) .
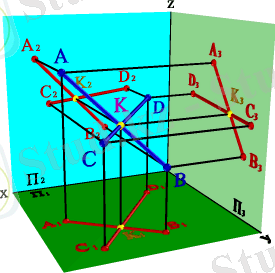
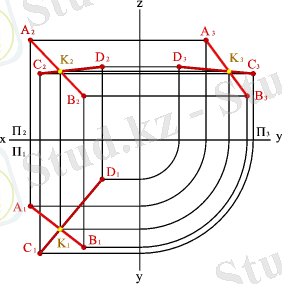 3. 21. -Сурет. Қиылысатын түзулер
3. 21. -Сурет. Қиылысатын түзулер
9. проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісі
Нүктелерді орын ауыстыру траекториясы проекциялар жазықтығына параллель. Траектория - шеңбердің доғасы, центрі проекциялар жазықтығына перпендикуляр өсте орналасқан. АВ (4. 4. - сурет) жалпы жағдайдағы түзу кесіндісінің шынайы өлшемін анықтау үшін, В 1 нүктесі арқылы өтетін горизонталь жазықтығына перпендикуляр айналдыру өсін аламыз. Кесіндіні фронталь проекциялар жазықтығына параллель болатындай етіп бұрамыз (кесіндінің гоизонталь проекциясы x өсіне параллель) . Осыған байланысты А 1 нүктесі А 1 *, m 2 нүктесіне орналасады, ал В нүктесі өз күйін өзгертпейді. А 2 * нүктесі А нүктесі траекториясының фронталь проекцияларының қиылысында орналасқан (түзу сызық x өсіне параллель ) . В 2 А 2 * алынған проекциясы кесіндінің өлшемін анықтайды.
11. Проекция жазықтығын алмастыру тəсілі
Проекция жазықтығын алмастыру тəсілінің маңызы - күрделі есептерді шешу үшін, көлденең П0 проекция жазықтығын бір жазықтықпен немесе екі жазықтықпен алмастыру арқылы есептің шешуін табуға болады. Егер геометриялық фигуралардың кескініне бірінші проекция жазықтығын параллель алсақ, онда екінші проекция жазықтығын сол кескінге перпендикуляр етіп орналастырамыз. Осы тəсілді пайдаланып, түзудің жəне жазықтықтың нақты шамасын, түзу мен жазықтықтың немесе екі жазықтықтың бұрыштық шамасын, нүкте мен жазықтықтың арақашықтығын жəне тағы басқа сол сияқты есептерді шешуге болады.
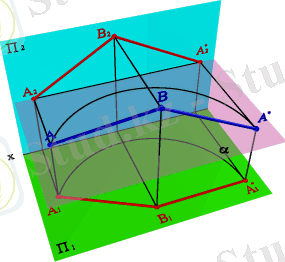
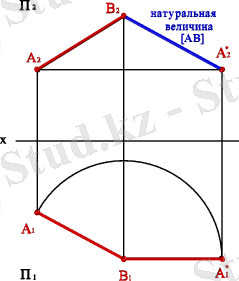 4. 4. - Сурет. Горизонталь проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісімен кесіндінің шынайы өлшемін анықтау
4. 4. - Сурет. Горизонталь проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісімен кесіндінің шынайы өлшемін анықтау
12. Екі түзудің өзара орналасуы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz