Көпөлшемді талдау

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

10-Лекция. Көпөлшемді талдау

Жоспары:

10. 1. Корреляциондық талдау.

10. 2. Регрессиондық талдау.

10. 3. Корреляциондық және регрессиондық талдаудың созылмалы- лық коэффициентін есептеу.

Мақсаты: Белгілі бір құбылыстардың байланысын өлшеу және оған әсер ететін факторларды таңдау, сонымен қатар оларды анықтап корреляциондық және регрессиондық талдаудың байланыстарының сандық мәнін олардың бар болмысының дұрыстығын ұғу. Корреляциондық және регрессиондық талдаудың созылмалылық коэффициентін есептеу.

Тақырып бойынша негізгі ұғымдар: Корреляция, регрессия, корреляциондық талдау, регрессиондық талдау, корреляцияның қос коэффициенттері, корреляцияның жұптық коэффициенттері, корреляциялық коэффициенттердің кризистік мәні, дербес коэффициент, корреляцияның терімді жиындық коэффициенттері, қадамдық регрессия, жұптық регрессия, құлаштық регрессия, ең кіші квадраттар әдісі, созылмалылық коэффициент.

Корреляциондық талдау

Корреляциондық талдау мынаны қамтамасыз етеді:

а) екі және оданда көп құбыластардың байланыс дәрежесін өлшеу;

б) құбылыстар арасындағы байланыстылықтың дәрежесін өлшеуге негізделген, нәтижелік белгіге елеулі әсер етіп факторларды теру (таңдау) ;

в) бұрын белгісіз болған байланыстарды анықтау (корреляция құбылыстардың арасынан себептік байланысты тікелей анықтамайды, бірақ бұл байланыстардың сандық мәнін және олардың бар болатындығы жайлы пікірлердің дұрыстығын орнатады.

Корреляциондық талдау жасауда барлық бірлестік (жиын) әрқайсысы n бақылауды қамтитын айнымалылар (факторлар) жиыны ретінде қарастырады; x _ik -к айнымалысының i-інші бақылауы

\[\overline{{x_{k}}}\]

к- айнымалысының мәні i=1, …, n.

Талдаудың негізгі заттары қос (жұпты), дербес корреляциялау коэффициенттері, корреляцияның жиындық коэффициенттері болып табылады. Корреляцияның қос коэффициенттері басқа факторлардың әсерін ортаға қатысты ескеркді. Бұл әсер етуді шығарып тастау үшін корреляцияның дербес коэффициенттері анықталады. К және L -ші факторлардың арасындағы корреляцияның жұптық коэффициент былай есептеледі:

\[r_{k p}=\sum_{i=1}^{n}{\Big(}{\it x}_{i k}-{\frac{\bf x}{\it k}}{\Big)}_{x_{i}}-{\frac{\bf\nabla}{\it x}_{i}}{\Big)}_{\hat{\mathrm{g}}_{i k}^{A}}^{\!\!n}\,\left({\it x}_{i k}-{\frac{\bf\nabla}{\it x}_{k}}\right){\frac{s}{\Delta}}^{\!\!n}\left({\it x}_{i L}-{\frac{\bf\nabla}{\it x}_{L}}\right){\frac{\bf\nabla}{\biggr|}_{k}^{\!\!-}}.\]

(10. 1)

Ол L -інші және k -шы факторлар терулері болып келетін кездейсоқ шамалардың бірлескен нормалды таралу жағдайында ғана сызықтық статистикалық байланыстың тығыздық көрсеткіші болады.

Осы шарттарда да корреляцияның жұптық коэффициенттерінің 0-ге теңдігі туралы гипотезаны тексеру үшін еркіндік дәрежесі n-2 болатын Стьюдент заңы бойынша жіктелген t -статистикасының кризистік мәні, ал соның негізінде корреляция коэффициенттерінің кризистік мәні былай есептелінеді:

\[r_{k_{p}}=t_{k_{p}}/\left(n-2+t^{2}\right)^{z}.\]

(10. 2)

Егер есептелінген мәні кризистіктен үлкен болса, онда сол коэффициенттің нольге теңдігі туралы гипотеза сәйкес ықтималдық дәрежесінде терістеледі. Осыған ұқсас қортынды корреляциясының дербес коэффициентінің маңыздылығын тексеруге орынды болады.

К-шы және L -ші факторлардың арасындағы бірінші ретті корреляцияның дербес коэффициенті j -ші фактордың бекітілген мәнінде олардың сызықтық байланыстарының тығыздығын сипаттайды. Ол мынамен анықталады:

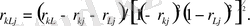(10. 3)

Ол жұптық коэффициентке ұқсас сондай шарттарда таралған, және оның маңыздылығын тексеру үшін еркіндік дәрежесі n-3 -ке тең t- статика қолданылады.

Дербес коэффициент жалпылай барлық айнымалылар белгілесек деген шартпен келесі түрде есептелінеді:

\[r_{k l}\left(\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\hat{n}\right)=-\left(D_{k l}\,D_{l}\,\right)^{\mathcal{N}},\]

(10. 4)

Мұндағы

\[D_{i j}\]

\[\frac{\sigma}{\Lambda}\]

-ші жолмен

\[\textstyle{\frac{v}{\hat{\mathcal{J}}}}\]

-ші бағананы сызып тастау арқылы коррелясияның жұптық коэффициентімен жасалған матрицаның анықтауышы.

Әрбір корреляцияның дербес коэффициенті үшін коэффициентің маңыздылығын тексеру үшін жұптыққа ұқсас t - мәні, және сондай-ақ сенімділігік коэффициенттері де есептелінеді. Мұнда z -түрлендірілген шаманың дисперциясы 1/(n-L-3) тең, мұндағы L-белгіленген айнымалылар саны (программада L=m-2 ) .

К-ші айнымалы мен қалған (түсіндіруші) айнымалылар арасындағы байланыс тығыздығын анықтау үшін корреляцияның терімді жиындық коэффициенті қолданылады:

\[R_{k}=(1-D/D_{k k})^{\frac{1}{2}}\]

, (10. 5)

мұндағы D- корреляцияның жұптық коэффициентінің матрица анықтауышы.

Жиындық корреляция коэффициентінің статистикалық маңыздылығын тексеру үшін L және (n-L-2) еркіндік дәрежесі F -таралуы бар:

\[F={\frac{R^{2}/L}{\left(1-R^{2}/(n-L-2\right)}}\]

, (10. 6)

шамасы қолданылады

Егер есептелінген F- мән сәйкес ықтималдылық деңгейде (0, 9 және жоғары) F-таралуының мәнінен көп болса, онда К-шы айнымылы мен қалған айнымалылар арасындағы сызықтық байланыс туралы гипотеза терістелмейді. Бағдарламада жиынның корреляциясының коэффициенттері үшін F-мәні және оған сәйкес келетін F-таралуының пайыздық нүктесі шығарылады.

Регрессиондық талдау

Регрессиондық талдауда келесі мәселелер шешіледі:

а) тәуелділіктің формаларын орнату (оң, теріс, сызықты, сызықты емес) ;

б) регрессия функциясын анықтау. Тәуелді айнымалының өзгеру тенденциясын көрсету ғана маңызды емес, сонымен қатар, егер басқа (екінші жәрежелі, кері) факторлар өзгермей (сол орташа деңгейде орналасса) және кездейсоқ элементтер шығарылса, онда негізгі факторлардың тәуелді айнымалыларына әсері қалай болатындығын да анықтау маңызды;

в) тәуелді айнымалылардың белгісіз мәндерін бағалау.

Қадамдық регрессия Y-түсіндіру үшін регрессиялардың жиынының жақсысын анықтайтын әдістердің бірі. Қадамдық регрессия теңдеуіне айнымалыларды кезектеп қосу арқылы жүзеге асады.

Құлаштық регрессия мультиколлинарлық шартында, яғни тәуелсіз айнымалылардың күшті корреляциясында, жиындық сызықтық регрессияны бағалауға бағытталған, құлаштық бағалауға негізделеді.

K-параметрін автоматты есептеу үшін

\[k=m s/a^{*}a\]

формуласы алынған, мұндағы а-регрессияның МНК бойынша бағасы.

Жұптық регрессия Y пен X айнымалысынан тәуелді функциясы арасында байланысты орнатады; яғни регрессия Y=f(x) түрінде болады.

Ағымдық пакетте жұптық регрессияғақосылған f функциясы екі негізгі шартқа қанағаттанады: Олар экономикалық зерттеулер практикасында таралған, регрессия теңдеулерінің әрқайсысы логарифмдеу және дәрежеге шығару арқылы түрлендірулер жолымен сызықтық модельге келтіріледі.

Жұптық регрессияның функцияларын іске асыру үшін Y(тәуелді айнымалы) айнымалысын, Х айнымалысын (түсіндіруші айнымалы), анықтау сондай-ақ жұптық регрессияның функциялар тізімін (1-4 кесте) құру қажет.

Әрбір функция үшін параметрлер ең кіші квадраттар әдісімен табылады, сонымен қатар

\[\begin{array}{l}{{{\propto}_{i}^{n}\sum_{i=1}^{n}{\mathfrak{G}}_{i}-\sum_{i}{\frac{2}{\phi}}{\frac{{\mathfrak{h}}}{\phi}}{\frac{{\mathfrak{h}}}{\phi}}(n-k)}}\end{array}\]

(10. 7)

түріндегі критерилер есептелінеді, мұндағы k-функцияның бағаланылатын параметрлер саны.

Критеридің минимальді мәні сәйкес келетін функциясы оптимальді деп саналады да, ол үшін барлық параметрлер есептелінеді.

Сызықтық емес байланыстың экономикалық интерпретациялау үшін әдетте, түсіндіруші айнымалының 1%-ке өзгергендегі тәуелді айнымалының салыстырмалы өзгеруін сипаттайтын сызылмалылық коэффициентті қолданылады. Егер регрессия теңдеуі y=f(x) түрінде берілсе, онда сызылмалылық коэффициентті былай есептелінеді:

\[{\hat{Y}}={\frac{d t}{d x}}{\frac{\cdot{\boldsymbol{x}}}{y}}\]

(10. 8)

мұндағы

\[{\overline{{x}}}\ -X\]

айнымалысының орташа мәні,

\[{\overline{{y}}}\ -y\]

айнымалысының орташа мәні, туынды

\[\overline{{\chi}}\]

нүктесінде алынады.

Дельта- коэффициент. Әрбір фактордың қосынды ықпалға үлесі

\[\mathbf{D}_{j}=(r_{j}\cdot\beta_{j})\,R\]

;

\[\sum_{k}\mathbf{D}_{k}=1\]

; (10. 9)

\[R^{2}=r_{1}b_{1}+r_{2}b_{2}+....+r_{k}\beta_{k}\]

(10. 10)

құрайды, мұндағы

\[R^{2}\]

- ; -жиындық детерминациялар коэффициентті,

\[\textstyle{\int_{\frac{1}{k}}}\]

-i-ші фактормен тәуелді айнымалы арасындағы жұптық корреляция коэффициентті,

\[b_{i}-\beta\]

- коэффициент.

10. 1-Кесте: Созылмалылық коэффициентті есептеу

Функция: Функция

Созылмалылық коэффициентінің формуласы: Созылмалылық коэффициентінің формуласы

Функция:

\[Y=a+b x\]

\[Y=a+b x+c x^{2}\]

\[Y=a+b/x\]

\[Y=1/(a+b x)\]

\[Y=1/(a+b)e^{-x}\]

\[Y=a e^{i\alpha}\]

\[Y=a+b\ln(x)\]

\[Y=a b^{\varepsilon}c^{\varepsilon}\]

\[Y=a b^{x}\]

10.

\[Y=a+b/\ln(x)\]

11.

\[Y=a x^{b}\]

12.

\[Y=a+b x+c(x)^{y}\]

\[Y=x/(a+b x)\]

14.

\[Y=a e^{(b/x)}\]

15.

\[Y=a+b x^{s}\]

16.

\[Y=a_{0}+a_{1}x^{1}+....+a_{k}x^{k}\]

Созылмалылық коэффициентінің формуласы:

\[{\hat{Y}}=b(x/y)\]

\[\bar{Y}=(b+2c x)(x/y)\]

\[{\bar{Y}}=b/(a x+b)\]

\[{\bar{Y}}=b x/(a+b x)\]

\[\zeta=b x e^{-x}\,/\left(a+b e^{-x}\right)\]

\[\bar{Y}=b x\]

\[Y=b/y\]

\[\zeta=a(\ln(b)e^{x}c^{x^{2}}+\angle b^{x}x e^{x^{2}}\ln(c))(x/\,y)\]

\[{\tilde{Y}}=a\ln(b)e^{x}(x/y)\]

\[\bar{Y}=b/(\ln^{2}(x)\times y)\]

\[\scriptstyle Y=b\]

\[{\tilde{Y}}=(b-c)(x)^{{\tilde{Y}}_{i}}(x/y)\]

\[Y=a/(a+b x)\]

\[Y=b/x\]

\[{\bar{Y}}=b k x^{k}/(a+b x^{k})\]

\[\zeta=(\sum_{i=1}^{k}a_{i}\dot{x}^{i})/y\]

Корректілі жүргізілген талдауда дельта-коэффициенттер шамасы оң, яғни барлық регрессия коэффициенттері корреляцияның сәйкес жұптық коэффициенттері қабылдайтын таңбаны алады.

Дегенмен түсіндіруші айнымалылардың күшті коррелирлеу жағдайында кейбір дельта-коэффициенттер корреляциясының жұптық коэффициенттеріне қарама-қарсы таңбасы бар регрессияның коэффициенттеріне сәйкес теріс болуы мүмкін.

Бета-коэффициент. Факторлардың ауытқымалылық дәрежесі және өлшеудегі айырмашылықтарын жою үшін

\[\bigwedge^{g}\]

- коэффициентті немесе стандартталған түрде регрессия коэффициентті қолданылады:

\[\beta_{j}=b_{j}S_{j}/S_{y}\]

, (10. 11)

мұндағы

\[b_{j}\]

- j -ші айнымалыдағы регрессия коэффициентті;

\[\mathbf{S}_{j}\]

- j -ші айнымалының орташа квадраттық ауытқуының бағасы,

\[S_{y}\]

-тәуелсіз айнымалының орташа квадраттық ауытқуының бағасы.