5-Лекция. Математикалық модельдеу және талдаудың экономика-математикалық тәсілдері

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

5-Лекция. Математикалық модельдеу және талдаудың экономика-математикалық тәсілдері

Жоспары:

5. 1. Экономика - математикалық модельдеу объектісі ретінде.

5. 2. Экономика - математикалық үлгілеу.

5. 3. Нәтижелік көрсеткіштердің өзгеруіне факторлардың сандық әсерін талдау әдістері.

Мақсаты: талдаудың математикалық тәсілін, экономика-математикалық үлгілеу, нәтижелік көрсеткіштердің өзгеруіне факторлардың сандық әсерін талдау әдістерін қарастыру.

Тақырып бойынша негізгі ұғымдар: корреляциялық (стохастикалық) байланыс, қос корреляция, көптік корреляция, вариация коэффициенті, орташашаршылық ауытқу, факторлық көрсеткіш, нәтижелі көрсеткіш, тузусызықтық байланыс, қисықсызықтық байланыс және т. б.

Модель дегеніміз объектінің (жүйенің) белгілі бір өзара байланыстары бар және оның қызметі мен дамуын сипаттайтын элементтерт комплексінің шартты бейнесі. Модель үрдістің мағынасын жинақты түрде сипаттауға көмектеседі. Құрылған модельден зерттелетін үрдістердің мазмұнын көруге болады.

Математикалық модельдермен зерттелетін объекті мен үрдістің қасиеттері, ерекшеліктері және сипаттамалары теңдеулер жүйелері, теңсіздіктер және функция арқылы көрсетіледі.

Көптеген математикалық модельдер универсалды болып келеді, яғни әртүрлі жүйелерді зерттеуге қолданылады. Математикалық модельдер қарастырылатын құбылыстар мен үрдістердің сандық заңдылықтарын анықтауға, сипатталатын факторлардың тәуелділігі мен өзара байланысын табуға мүмкіндік береді. Математикалық модельдердің дамуына өте күрделі есептеулерді жүргізетін электронды-есептегіш машиналарының көбеюі зор ықпал етті.

Көптеген математикалық модельдер параметрлер мен айнымалылардан тұратын теңдеулер мен теңсіздіктер жүйелерінен тұрады. Айнымалы шамалар, мысалы, өндірілген өнім көлемі, капитал жұмсау, тасымалдау т. с. с., ал параметрлер өнімді өндіруге жұмсалған материал, уақыт, шикізат шығынының мөлшерін көрсетеді. Әрбір модельде айнымалылардың екі тобын көрсетуге болады. 1) Сыртқы айнымалылар - олардың мәндері модельден тыс және берілген; 2) Ішкі айнымалылар, олардың мәндері берілген модельді зерттеу қорытындысында анықталады.

Модельдеу үрдісінің нақты алгоритмі жоқ, бірақ модельдеу тәжірибесінде басшылықққа алатын анықталған принциптер бар.

Математикалық модельдердің құрылымдық және функционалдық түрлері бар. Құрылымдық модельдер жүйелердің құрылымын және оның элементерінің өзара әсерін зерттейді. Функционалдық модельдер жүйенің ішкі құрылысына байланыссыз әртүрлі жағдайдағы тәртібін талдайды.

Құрылымдық модельді оқып үйрену үстінде объектінің мазмұнын туралы, оның сыртқы жағдайларға әсері туралы информацияларды алуға болады. Ал функционалдық модельді зерттегенде объектінің әртүрлі реакцияларының сыртқы ортаға әсері туралы деректер алуға болады. Сонымен қатар объектінің құрылымын талдауға және құрылымдық модельдерді құруға мүмкіндіктер туады.

Экономикалық-математикалық модельдер жүйе жағдайын болашақты жоспарлау мен болжауға пайдаланады. Мұндай жағдайда модель оның негізінде қойылған белгілі бір алғы шарттарға сәйкес экономикалық үрдістердің ағымын көрсетеді. Жоспарлау мен болжау модельдерінде алғышарттарды дұрыс таңдау ерекше маңызды роль атқарады. Модель есептің шарты дұрыс қойылған кезде ғана нақты жүйелердің құрылысы мен функциясын дұрыс сипатайды.

Экономикалық-математикалық модельдер сипаттаулы және оптималды болып бөлінеді.

Экономикалық жүйелердің сипаттаулы моделі есептерді математикалық формула түрінде көрсетеді және жүйе жағдайы мен оның элементтерінің байланысын тереңірек ұғып үйренуге қолданылады. Мұндай модельдерге халық шаруашылығы және экономикалық аудандардың салааралық байланысының матрицалық моделі жатады. Осындай типті есептің модельдері анықталған алғашқы мәліметтері бойынша бір ғана шешімі болады. Бұл модельдердің негізгі кемшілігі - ең тиімді (оптималды) шешімін іздейтін шарттың жоқтығы.

Оптималды модельдерде экономикалық есептің мағынасы математикалық формула түрінде жазылады және ең тиімді шешімі табылатын шарт функция түрінде көрсетіледі. Бұл модельдер белгілі бір алғашқы мәліметтер бойынша есеп шартын қанағыттандыратын көптеген шешімдер және оптималдықтың критерийіне сәйкес тиімді шешім алуға мүмкіндік береді. Мұндай модельдерге өндірістік программаны оптималдау, кесіп-пішуді оптималдау, қоспа компоненттерін оптималдау, кәсіпорынды орналастыруды оптималдау, көлік есептерінің модельдері жатады.

Оптималдық модельдердің көпшілігінде оптиалдықтың бір ғана критерийі қарастырылады.

Математикалық модельдерде сызықтық және сызықтық емес тәуелділіктердің әртүрлі түрлері қолданылады.

Математикалық модельдеу үрдісінің негізгі бөлігі аппроксимация (жуықтау) - математикалық амалдарды (функция, теңдеу т. с. с. ) басқа қарапайым шамалар арқылы жуықтап табу болып табылады. Аппроксимацияның көмегімен күрделі есептерді жай есептерге, сызықтық емес теңдеулерді сызықтық теңдеулерге келтіреді.

Модельденетін обьектінің белгілі бір уақытқа немесе уақыт аралығына сәйкес қасиеттерін сипаттайтын математикалық модельдер статикалық деп аталады.

Үрдістердің белгілі бір уақыт аралығындағы өзгерістерін зерттейтін модельдер динамикалық деп аталады.

Детерминистикалық (латынша determino - анықтау) модельдер дегеніміз барлық параметрлері және сыртқы айнымалылары бірге тең ықтималдықпен анықталатын модельдер.

Ықтималдық модельдерінде параметрлер мен сыртқы айнымалылар немесе олардың белгілі бір бөлігі тиісті ықтималдықтың үлестіруімен сипатталады.

Анықталмағандықты есепке алатын модельдерге ықтималдық теориясының заңдарын қолдануға болмайды.

Математикалық модель жасау процесі өзара байланысқан бірнеше кезеңнен тұрады.

Бірінші кезең - есептің қойылуы. Бұл кезең зерттеудің мақсатын анықтаудан басталады.

Мысалы, кәсіпорын үшін өнім өндіру немесе жүк тасымалдаудың оптималды жоспарын құру немесе берілген материалды кесіп-пішудің оптималды нұсқасын табу қажет т. с. с. Зерттеудің мақсатына сәйкес жүйелерді жан-жақты талдап, оның құрылымы мен қызметін, ерекшелктерін ескеру керек.

Жүйелерді модельдеген кезде модельге есептің шешіміне әсер ететін, яғни қойылған мақсатқа қол жеткізетін факторлардың енуі шарт.

Екінші кезең - таңдалып алынған жүйелерге математикалық модельдер құру. Бұл кезеңде есепті формула түріне келтіру - математикалық тәуелділіктерді теңдеулер, теңсіздіктер түрінде құру жүргізіледі.

Алдағы уақытта есептердің математикалық формула түрінде жазылған өрнектерін есептің моделі деп атаймыз.

Үшінші кезең - құрылған модельге сәйкес есептің шешімін алу. Бұл кезеңнің негізгі есептерін қарастырайық. Біріншіден, модельге қажетті алғашқы ақпараттарды жинау, параметрлер мен сыртқы айнымалылардың сандық мәндерін анықтау қажет. Екіншіден, есептің шешімін алатын әдісті таңдап алу керек. Сандық экономикалық-математикалық әдістердің арасында кеңінен тарағандары симплекс әдісі және потенциал әдісі. Олар көптеген экономикалық есептерді шығаруға қолданылады. Бұл әдістермен шығаруға келмейтін есептер де кездеседі. Мұндай жағдайларда жүйелерді зерттеудің эвристикалық және имитациялық әдістері қолданылады.

Эвристика (грек сөзінен - табамын, ойлап табамын, ашамын) - зерттеушінің интуициясы мен жүргізген тәжірибесіне сәйкес шешілетін әдістердің жиынтығы.

Имитация - модельдеудің мүмкіндігін кеңейтетін жаңа бағыт болып табылады. Имитациялық модельдеуді нақты жүйелердің модельдеріне жүргізілген эксперимент ретінде түсінуге болады, ал жеке алғанда математикалық модельдеудің көмегімен алғашқы шарттарын өзгерте отырып жүргізілетін есептеу эксперименті.

Имитация (латынша - еліктеу) - жасанды құралдардың көмегімен бір нәрсені жаңадан ендіру немесе еске түсіру.

Төртінші кезең - модель бойынша алынған қорытындыны тәжірибеде қолдану. Математикалық әдістердің көмегімен алынған шешімдер талданып, белгілі бір аралықта алғашқы ақпараттарға тигізетін әсері тексеріледі.

Уақыттың өзгеруіне сәйкес алғашқы ақпараттар өзгереді, сол өзгерістердің алынатын шешімдерге тигізетін әсерін білу аса маңызды.

Алдынғы тарауларда факторлық зерттеудің шарттарын шешуі қарастырылды. Бірақ тәжірибеде барлық экономикалық құбылыстар мен процесстер осы методика арқылы орындалады, себебі факторлық көрсеткіштің мөлшеріне нәтижелік көрсеткіштің жалғыз мөлшері сәйкес келгенде олардың көбісін функционалдық тәуелділікпен қосуға болмайды.

Экономикалық зерттеулерде стохастикалылығымен ерекшеленетін корреляциялық тәуекелділіктер жиі кездеседі. Бұл жерде әрбір факторлық көрсеткіштің мөлшеріне нәтижелік көрсеткіштің бірнеше мағынасы сәйкес келеді. Мысалы, жұмысшы еңбегінің қормен жарақтануы өсуі әртүрлі кәсіпорындарда әртүрлі еңбек өнімділігінің өсуін береді. Ол еңбек өнімділігіне ықпал етуші барлық факторлар өзара байланыста және кешенді болатынымен түсіндіріледі. Әр түрлі факторлардың қандай оптималдықта үйлесуінен байланысты нәтижелік көрсеткішке олардың әрқайсысының ықпал ету деңгейі бірдей болмайды.

Зерттелетін факторлар мен нәтижелік көрсеткіштердің арасындағы байланысты зерттеу үшін көп объектілерді алып, олардың мәндерін салыстырғанда шығады. Сонда үлкен сандар заңына сәйкес басқа факторлардың нәтижелік көрсеткішіне әсері жойлады. Бұл зерттелуші құбылыстардың арасындағы қатынасты құруға мүмкіндік береді.

Корреляциялық (стохастикалық) байланыс - бұл жаппай бақылауда ғана байқалатын көрсеткіштердің арасындағы толық емес мүмкінді байланыс. Қос және көптік корреляцияны бөліп айтамыз.

Қос корреляция - бұл екі көрсеткіштің арасындағы байланыс: біріншісі- факторлық, екіншісі- нәтижелік.

Көптік корреляция - бірнеше факторлардың нәтижелік көрсеткішпен өзара қатынасынан пайда болады.

Корреляциялық қатынастарды зерттеу үшін келесі экономикалық зерттеудің тәсілдері қолданылады: қатарласқан және динамикалық қатарларды салыстыру, графиктер, аналитикалық топтастыру. Бірақ олар байланыстың жалпы сипатын және бағытталуын көрсетеді. Факторлық талдаудың негізгі міндеті - әрбір фактордың нәтижелік көрсеткішке әсерін анықтау. Бұл мақсат үшін корреляциялық, дисперсиялық, компоненттік, көпөлшемді факторлық талдаудың тәсілдері қолданылады.

Корреляциялық зерттеуді қолданудың қажетті шарттары, жағдайлары:

Зерттелуші факторлар мен нәтижелік көрсеткіштердің шамасы жөнінде жеткілікті үлкен бақылаулар саны болуы;
Зерттелуші факторлардың сандық өлшемі және ақпарат көздерінде сипаты болуы тиіс.

Корреляциялық талдауды пайдалану келесі міндеттерді шешуге жол береді:

1) бір немесе бірнеше факторлардың әсерінен нәтижелік көрсеткіштің өзгерісін анықтау;

2) нәтижелік көрсеткіштің әрбір фактордан тәуелділік деңгейін айқындау.

Корреляциялық зерттеудің негізгі міндеттерінің бірі ретінде факторлардың нәтижелік көрсеткішке (абсолюттік өлшемде) әсерін анықтау. Бұл міндетті шешу үшін сәйкес математикалық теңдік тандалады. Ол зерттелуші байланысты бейнелеуі (тузусызықтық, қисықсызықтық және т. б. ) тиіс. Бұл корреляциялық талдауда маңызды роль атқарады. Себебі, регрессияның теңдігін дұрыс тандаудан есептің нәтижелері және шешуі байланысты.

Байланыс теңдігінің негізделуі қатарласқан қатарларды салыстыру, топтық деректердің және сызықтық графиктердің көмегімен жасалады. Нүктелердің графикте орналасуы зерттелуші көрсеткіштердің арасында (тузусызықтық, қисықсызықтық және т. б. ) қандай байланыс құрылғанын көрсетеді.

Қарапайым теңдіктің бірі - екі көрсеткіш арасындағы тузусызықтық тәуелділікті сипаттайды:

У _х = а + в*х (5. 1)

Мұндағы х- факторлық көрсеткіш; У- нәтижелік көрсеткіш;

а және в- табу керек регрессиялық теңдікьің параматрлері.

Бұл теңдік факторлық көрсеткіштің белгілі бір шамаға өзгеруімен байланысты нәтижелік көрсеткіштің мәнінің бірқалыпты өсуі немесе төмендеуі байқалатын екі белгі арасындағы байланысты сипаттайды.

а және в коэфициентінің мәндері кші квадраттар әдісі бойынша алынған теңдік жүйесінен алынады. Бұл жағдайда теңдік жүйесі келесі түрге тән:

{ na + b∑x = ∑y (5. 2)

{ a∑x + b∑x² = ∑xy (5. 3)

Мұндағы n- бақылау көлемі, мәндері ∑х, ∑у, ∑ху, ∑х²- берілген нақты деректерің негізінде есептелінеді.

Осы қағида бойынша зерттелуші құбылыстардың арасындағы қисықсызықты тәуелділігі байланысы теңдігі шешіледі.

Егер бір көрсеткіштің өсуімен басқа көрсеткіштің мәні белгілі бір деңгейге дейін өссе, ал содан соң төмендей бастаса, онда бұндай байланысты жазу үшін екінші деңгейдегі парабола сәйкес келеді:

У _х = а + вх + сх² (5. 4)

Кіші квадраттар әдісіне сәйкес а, в, с параметрлерін анықтау үшін келесі теңдік жүйесін шешу керек:

{ nа + в∑х + с∑х ²= ∑у

{ а∑х + в∑х² + с∑х ³= ∑ху (5. 5)

{ а∑х² + в∑х³ + с∑х ⁴ = ∑х²у

∑х, ∑у, ∑ху, ∑х²у, ∑х², ∑х³, ∑х ⁴ - мәндерін берілген деректердің негізінде анықталады.

Көбінесе, экономикалық анализда қисық сызықты тәуекелділерде гипербола қолданылады:

Y _x = a + b/x (5. 6)

Оның параметрлерін анықтау үшін келесі теңдеу жүйесін шешу қажет:

{ na + b∑ 1/x = ∑y;

{ a∑1/x + b∑(1/x) ² =∑ (1/x) y. (5. 7)

Гипербола екі көрсеткіш арасындағы тәуелділікті бейнелеп көрсетеді. Біріншісінің ауыспалы мәні белгілі бір деңгейге дейін өскен уақытта, келесісің мәні белгілі бір деңгейге көтеріледі, содан кейін өсіңкілік төмендей бастайды.

Анағұрлым күрделі жағдайларда зерттелуші құбылыстар арасында күрделі параболалар (үшінші, төртінші дәрежелік), сонымен қатар квадраттық, дәрежелік және т. б. пайдаланылады.

Сонымен, осы не басқа да математикалық теңдеулерді қолданумен, зерттелетін құбылыстар арасындағы тәуелділік деңгейін анықтауға болады. Бірақ байланыс тығыз ба, жоқ па, берілген фактордың нәтижелік көрсеткіштің шамасына әсері шешуші ме, әлде жанама ма, регрессиондық талдау жауап бермейді.

Факторлық және нәтижелі көрсеткіштер арасындағы байланыс тығыздылығын өлшеу үшін корреляция коэффициенті анықталады.

Зерттелетін көрсеткіштер арасындағы байланыс түзу сызықтық жағдайда корреляция коэффициенті мына формула бойынша есептеледі:

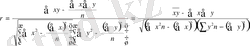(5. 8)

Корреляция коэффициенті 0-ден ±1-ге дейін мәндерді қабылдайды. Оның мөлшері 1-ге жақын болған сайын, зерттелетін құбылыстар арасындағы байланыс тығыздығы көбееді және керісінше.

Егер корреляция коэффициентін квадраттасақ, онда детерминация коэффициентін аламыз.

Қисық сызықты форма тәуелділігінде байланыс тығыздығын өлшеуде, мұнда түзу сызықты коэффициент емес, корреляциялық қатынас анықталады:

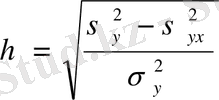(5. 9)

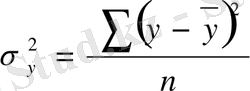
мұнда, 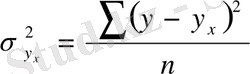(5. 10)

Бұл көрсеткіш универсалды болып табылады Оны кез келген тәуелділік формасында қолдануға болады. Бірақ оның мөлшерін анықтау үшін, алғашында регрессия теңдеуін (Y _x ) мен нәтижелі көсеткіштің мағынасын есептеу, содан алынған теңдеуге x және x ² мәндерін жас топтарына сәйкес қоямыз.

Корреляциялық талдаудың көптікті методикасы. Экономикалық құбылыс пен кәсіпорынның шаруашылық қызметінің процессы көп көлемді факторларға тәуелді болады. Ережеге сәйкес, әрбір фактор жекеше түрде зерттелінетін құбылыстарды барлық толықтықта анықтай алмайды. Факторлар кешені ғана және олардың өзара байланысында ғана зерттелуші құбылыстар сипаты жөнінде анағұрлым толық көрініс бере алады.

Көп факторлы корреляциялық талдау бірнеше кезеңдерден тұрады.

Бірінші кезеңде зерттелуші көрсеткішке факторлардың ықпалын анықталады және корреляциялық талдау үшін анағұрлым маңыздылары іріктеліп алынады.

Екінші кезеңде корреляциялық талдау қажет бастапқы ақпараттар жиналады және бағаланады.

Үшінші кезеңде нәтижелі көрсеткіш пен факторлар арасындағы өзара байланыс сипаты зерттеліп, үлгіленеді және зерттелуші байланыстың мәнін анағұрлым толығырақ мазмұндайтын математикалық теңдеу таңдалып негізделеді.

Төртінші кезеңде кореляциялық талдаудың негізгі көрсеткіштерінің байланысының есебі жүргізіледі.

Бесінші кезеңде корреляциялық талдаудың нәтижелеріне және практикалық қолданылуына баға беріледі.

Корреляциялық талдау үшін факторларды таңдау экономикалық талдауда маңызды кезең болып табылады. Қаншалықты дұрыс таңдау жасаудан, талдау қорытындысының нәтижесі дәл болады. Факторларды таңдау кезіндегі басты ролі теория, сонымен қатар талдаудың практикалық тәжірибесі болып табылады. Бұл жағдайда келесі ережелерді ұстану қажет:

Факторларды таңдаған кезде бірінші кезеңде көрсеткіштердің арасындағы себепті-салдарлы байланысын ескеру қажет, өйткені тек олар ғана зерттелетін құбылыстардың маңызын ашылады. Ал нәтижелік көрсеткішпен тек математикалық арақатынаста болатын факторлардың талдауының практикалық мәні болмайды.
Көп факторлы корреляциялық моделді жасаған кезде нәтижелі көрсеткішке шешуші әсер ететін тек мәнді факторларды ғана таңдау қажет, өйткені практика жүзінде барлық жағдайларды қамту мүмкін емес.
Барлық факторлар сандық өлшемді болуы міндетті, бұл өлшем бірлігі болу қажет және есеп пен есептілікте олар туралы ақпарат сақталу міндетті.
Сызықтық үлгідегі корреляциялық модельге нәтижелік көрсеткішпен байланысы қисықсызықтық жағдайда болатын факторларды еңгізу ұсынылмайды.
Корреляциялық модельге өзара байланысты факторларды еңгізу ұсынылмайды. Егер екі фактор арасындағы қос корреляциялық коэффициенті 0, 85-н жоғары болса, онда корреляциялық талдау ережеге сәйкес оның бірін шығарып тастау керек, әйтпесе бұл талдау нәтижелерін дұрыс көрсетпейді.
Корреляциялық модель құрамына нәтижелі көрсеткішпен байланысы функционалдық сипатқа ие факторларды еңгізуге болмайды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.