12-Лекция. Модельдердің өзгешеліктерін анықтау мәселелері

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

12-Лекция. Модельдердің өзгешеліктерін анықтау мәселелері

Жоспары:

12. 1 Екі классикалық модельдердің бірін таңдау. Теориялық акпектілер.

12. 2 Екі классикалық модельдердің бірін таңдау. Тәжірибелік аспектілер.

12. 3 бар болуы жағдайында модельдер өзгешеліктерін анықтауды кеңістіктік таңдау.

12. 4 Уақыттық қатарлардағы регрессия модельдерінің өзгешеліктерін анықтау.

12. 5 Экономикалық талдаудың маңыздылығы.

Мақсаты: Екі классикалық модельдердің теориялық және тәжірибелік аспектілерін, бар болуы жағдайында модельдер өзгешеліктерін анықтауды кеңістіктік таңдауды түсіну. Уақыттық қатарлардағы регрессия модельдерінің өзгешеліктерін анықтау, сонымен қатар экономикалық мәліметтерді талдаудың маңыздылығын білу.

Тақырып бойынша негізгі ұғымдар: Екі классикалық модель, гетероскедастикалылық моделі, теориялық және тәжірибелік аспекты, ұзын және қысқа модель, ковариация теңдеуі, уақыттық бақылау, регрессия моделі.

Екі классикалық модельдердің бірін таңдау. Теориялық аспектілер.

Бұл бөлімде 1-6 шартарын қанағаттандыратын классикалық модельдің өзгешеліктерін анықтау мәселелерін қарастырамыз. Сәйкес есеп келесі түрде жазылуы мүмкін. Регрессорлар - Х және Z екі тобына бөлінсін, мұндағы Х регрессоры маңызды болып табылады және ондағы параметрлер максималды мүмкін дәлдікпен бағалауды талап етеді; Z регрессорлары және оның параметрлері Х регрессорына қарағанда маңызды емес болып саналады. Келесі модельдердің бірін таңдау керек:

(12. 1)

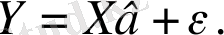(12. 2)

Өзгешеліктерді анықтау есептерін шешу барысындағы (12. 1) моделі - «ұзын», ал (12. 2) моделі - «қысқа» деп аталады. Мұндағы 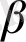мәнінің ақиқат мәні екі модельде де бірдей. Сондықтан, осы параметрді бағалау қажет.

(12. 1) және (12. 2) модельдерінің арасында таңдау жасау үшін, ең алдымен дұрыс деп тану критерийін анықтап алу қажет.

Ондай критерийлер екеу болуы мүмкін.

1. 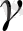коэффициенттерін нөлге теңестіру жағдайында 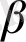параметрінің ақиқат мәні өзара тең болады, бірақ (12. 1), (12. 2) модельдерінен ең кіші квадраттар әдісінің көмегімен алынған 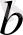бағасының мәні әр түрлі болады. Осыдан ақиқат мәніне «жуық» бағаны дұрыс деп тану қажет. «Жуықтаудың» мұндай сипаттамасы болып

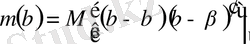
ауытқуының орташа квадраты табылады. Мұндағы 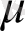- р ретті квадратты матрица, р - Х регрессорларының саны. А квадраттық матрицасы В матрицасына қарағанда «үлкен» деп аталады, егер олардың айырмасы А-В оң анықталған болса.

Осылайша, (12. 1), (12. 2) модельдерінің ішінен 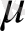кіші шамасынан тұратын 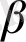бағасы алынатынын таңдау керек.

2. 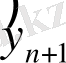- регрессорлардың әлі бақыланбаған мәндері үшін модельдерден алынатын болжамды мәні. 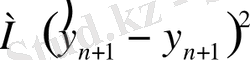шамасы болжамның орташа қатесі ретінде қарастырылуы мүмкін. Бұл қате кіші болатын модельдерді таңдау қажет.

1 және 2 критерийлері (яғни, 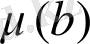немесе 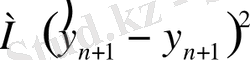минимум бойынша модель таңдау) бір-біріне тепе-тең екенін көрсетуге болады. Олардың шарттары Я. Магнуспен алынған қатынастың көмегімен жазылады. Бұл бөлімде бірнеше жеңілдетілген формаға сәйкес нәтижежелерді аламыз.

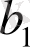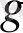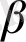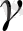, - (12. 1) моделінен ең кіші квадраттар әдісінің көмегімен алынған және параметрлерінің бағалары; 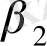- моделінен алынған 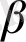бағасы болсын.

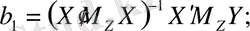(12. 3)

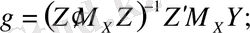(12. 4)

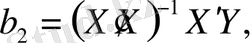(12. 5)

мұндағы 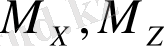- келесі түрдегі матрицалар:

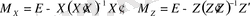
( Е - бірлік матрица) . Мұндағы 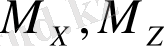матрицалары идемпотентті болып табылатынын ескере кетейік.

Тікелей әділдігіне оңай көз жеткізуге болатын қатынасты алайық:

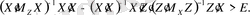
Бұл қатынасты қолдана отырып, (10. 3) теңдігін келесі түрде жазуға болады:

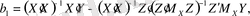
яғни,

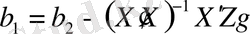(12. 7)

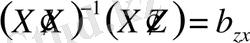деп белгілейік. 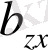матрицасының түрі экономикалық модель параметрінің бағасы сияқты екенін ескере кету қажет. Алайда, 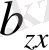формальды түрде баға деп айтуға болмайды, өйткені X, Z шамалары - кездейсоқ емес.

(10. 7) теңдігін келесі түрде жазайық:

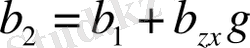. (12. 8)

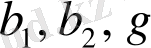бағаларының ковариациялық матрицаларын есептеу үшін формуланы келтірейік (аралық есептеуді қоса ала отырып) :

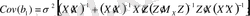
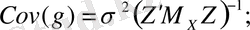(12. 9)

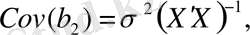
мұндағы 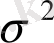- 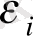дисперсиясы.

(12. 9) формуласын қолдана отырып, келесі өрнекті аламыз:

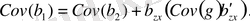(12. 10)

Алынған (12. 8) және (12. 10) нәтижелеріне талдау жасайық. Классикалық модель шарттарының орындалу күшінің кез келген жағдайында 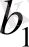бағасы ығыспаған болып табылады ( 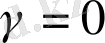және 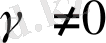жағдайында да) .

Егер 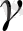ақиқат мәні нөлге тең болмаған жағдайда 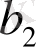бағасы 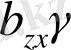ығысуымен ығысқан болып табылатынын (12. 8) теңдігі арқылы көруге болады. Онда ығысудың анық түрі оның оң екенін көрсетеді, егер X пен Z қатынастары бойынша Z «бірдей бағытталған» болса, және кері жағдайда теріс болатын болса.

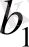бағасы кез келген жағдайда 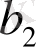бағасына қарағанда үлкен ковариацияға ие екендігін (12. 10) теңдігі арқылы біле аламыз.

(12. 8) - (12. 10) формулаларынан келесілерді аламыз:

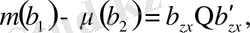(12. 11)

мұндағы 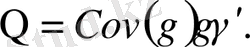(12. 12)

Осыдан, келесі шешімді жасай аламыз:

Егер (12. 12) матрицасы оң анықталған болып табылса, яғни тек оң меншікті мәндерге ие болатын болса, онда (12. 2) моделі 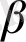параметрін (12. 1) моделі дұрыс болса да жақсы бағалайды.

Егер (12. 12) матрицасы оң да, теріс те меншікті мәндерге ие болатын болса, онда сұрақ бірмәнді шешіле алмайды. Бұл жағдайда егер (12. 12) матрицасы оң болатын болса, (12. 2) қысқа моделін дұрыс деп тану мүмкін болады.

Енді болжам қателігінің минималдылық критерийіне жүгінейік. (12. 1) моделі жайдайында 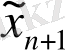, яғни 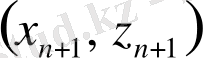бақылауы және (12. 2) моделі жағдайында 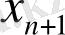бақылауы табылсын. Бұл жағдайлардағы болжамды мәндер келесідей:

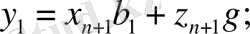(12. 13)

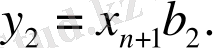(12. 14)

(12. 14) кездейсоқ шамасы 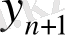кездейсоқ шамасының бақыланатын мәні сияқты математикалық үмітке ие. Тікелей есептеулер болжамның орташа қателері үшін келесі мәндерді береді:

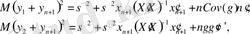
мұндағы

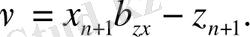
Демек,

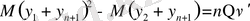(12. 15)

мұндағы - (12. 12) матрицасы.

Осылайша, мұндағы (12. 12) матрицасының оң анықталуы 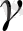параметрінің ақиқат мәні нөлге тең болмаса да (12. 2) қысқа моделінің ең қолайлы екендігін білдіреді.

Егер (12. 12) матрицасы оң да, теріс те меншікті мәндерге ие болатын болса, онда (12. 2) «қысқа» моделін таңдауға болады.

(12. 12) түріндегі матрица сонда және тек қана сонда оң анықталған болып табылады, егер келесі шарт орындалатын болса:

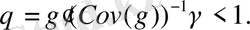(12. 16)

Осылайша, (10, 2) моделі математикалық көзқарас бойынша (12. 16) шарты орындалған жағдайда (10, 1) моделіне қарағанда ең қолайлысы болып табылады.

Екі классикалық модельдердің бірін таңдау. Тәжірибелік аспектілер

(12. 6) теңдігінің сол жақ бөлігінде тұрған 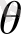шамасы 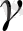белгісіз параметрінен тәуелді болады, яғни бақыланбайтын болып табылады, сондықтан алдыңғы бөлімде алынған критерий тәжірибеде (12. 1) және (12. 2) модельдерінің арасынан альтернативті таңдауды қалай жүзеге асыру керек деген сұраққа әлі жауап бере алмайды.

Шындығында да, тек баға мәнін ғана орналастырамыз:

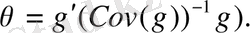
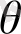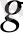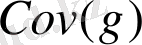шамасын түрлендірейік. Ол үшін және бағаларын ыңғайлы формаға келтірейік. Яғни,

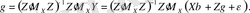
Матрицаларды тікелей көбейте отырып, 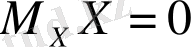теңдігіне оңай көз жеткізуге болады. Осылайша, келесі өрнекті аламыз:

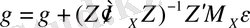(12. 17)

Сонымен қатар,

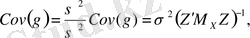
мұндағы 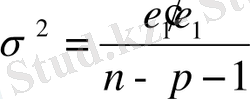- 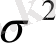параметрінің бағасы, 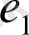- (12. 1) регрессия қалдықтарының бағанасы. Осыдан, (3. 17) теңдігін қолдана отырып, келесі теңдікті аламыз:

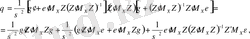
немесе 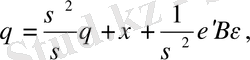(12. 18)

мұндағы

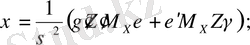
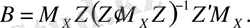
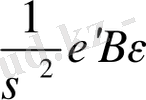шамасы тек оң мәндер қабылдаған жағдайда ғана 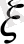шамасы тең ықтималдықты оң да, теріс те, мәндер қабылдай алады. Егер п бақылаулар саны айтарлықтай үлкен болатын болса, 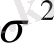мәні және 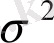бағалары соншалықты жуық мәнді болады. Олай болса, (10. 18) теңдігін қолдана отырып, 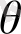бақыланатын шамасының және 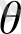параметрінің ең кіші мәндерін есептей аламыз. Жекелеп алғанда:

Егер 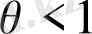болса, онда 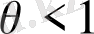деп жорамалдауға болады.

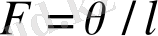(мұндағы 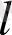- Z регрессорлар саны) шамасы (12. 1) моделінде 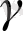коэффициенттерін нөлге теңестіру туралы гипотезаны қарапайым тестілеу барысында қолданылатын статистиканың бақыланатын мәні екенін көре аламыз. Егер 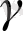параметрі шынында да нөлге тең болса, онда 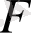шамасы Фишер-Снедекор жіктелуіне ие.

Шынында да, бұл статистиканың нақты түрі келесідей:

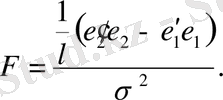(12. 19)

Сонымен қатар, (12. 9) қолдана отырып, келесі өрнекті аламыз:

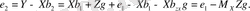
Осыдан

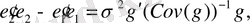(12. 20)

тең және тұжырым (12. 20) -ны (12. 19) -ға қоюмен дәлелденеді.

Осылайша, модельді баламалы таңдаудың келесі тұрғысы ұсынылуы мүмкін: с кейбір мәні таңдалады. Егер 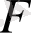- статистикасының бақыланатын мәні с -дан кіші болса, онда (12. 2) моделі дұрыс деп танылады, егер с -дан үлкен болса - онда (12. 1) моделі таңдалады.

Сонымен, жалпы айтқанда с мәні еркін түрде 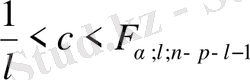шекарасынан таңдалады, мұндағы .

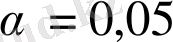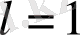ұқсас жағдайын қарастырайық, яғни бір Z регрессоры табылады. Бұл жағдайда 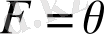. (12. 18) қолдана отырып, дұрыс деп танылатын келесі критерийді аламыз:

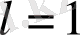(бір «бәсекелі» регрессордың бар болуы) жағдайында (12. 2) моделі (12. 1) моделіне қарағанда дұрыс деп танылады, егер 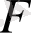- статистикасының бақыланатын мәні 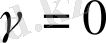гипотезасын тестілеу барысында 1-ден кіші болатын болса.

Келтірілген критерийдің тағы бір формуласын алайық. (12. 1), (12. 2) регрессияларына сәйкес:

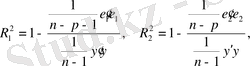
өрнектерін аламыз, мұндағы .

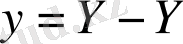Бұдан

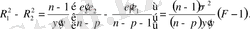(12. 21)

Осылайша, (12. 2) моделі (12. 1) моделіне қарағанда дұрыс деп танылады, егер Z регрессорларын жою кезінде детерминицияның түзетілген коэффициенті жоғарылайтын болса (12. 1) моделі детерминациясының қарапайым коэффициенті (12. 2) моделіне қарағанда әрқашан да жоғары екенін ескере кетейік) .

бар болуы жағдайында модельдер өзгешеліктерін анықтауды кеңістіктік таңдау

Кеңістіктік таңдау моделі жағдайында модельге тыңғылықты айнымалылардың қосылмау көрсеткіші болып түзетілмейтін гетероскедастикалылық табылады.

жоюдың ең жиі қолданылатын процедуралары 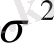регрессия қателерінің дисперсиясы қандайда бір регрессорлар функциясы болып табылады деген жорамалған негізделген екенін ескере кетейік. Егер 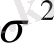дисперсиясы Z регрессорына тәуелді болса, ал модельдердің өзгешеліктерін анықтау барысында Z регрессоры модельге қосылмаған болса, онда стандартты процедуралар жоя алмайды.

Келесі мысалды қарастырайық. Гистограмманың X, Z - регрессорлары, Y - түсіндірілетін шамалары және жіктелудің негізгі сандық сипаттамалары

Y -тің X -тен тәуелділігінің сызықты регрессиясын бағалайық, яғни келесі модельді қарастырайық:

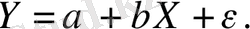(12. 23)

Ең кіші квадраттардың қарапайым әдісін қолдана отырып, келесі теңдеуді аламыз:

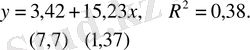
Алынған теңдеуге тексерудің Уайт тестін қолдану келесі нәтижені береді:

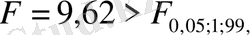
яғни, модель гетероскедастикалық болып табылады.

Модельдің теңдеуіне ең кіші квадраттардың зілдемелі әдісін қолданамыз. Онда регрессия теңдеуі келесі түрге ие болады:

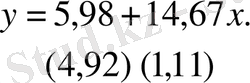
Бұған Уайт тестін қолдана отырып,

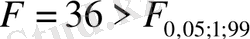
аламыз, яғни гомоскедастикалық туралы гипотеза тағы да жоққа шығарылады.

Модельге Z регрессорын қоса отырып, бұл жағдайды түзеп көрейік, яғни 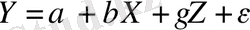моделін бағалайық.

Ең кіші квадраттардың қарапайым әдісінің көмегімен регрессияның келесі теңдеулерін аламыз:

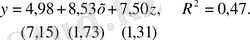
Уайт тесті 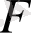- статистикасының 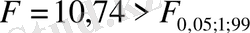мәнін беретіндіктен, бұл модель гетероскедастикалы болып табылады.

Алайда, гомоскедастикалылық туралы гипотеза әлдеқашан қолданылатын ең кіші квадраттардың зілдемелі әдісін қолданғаннан кейін келесі теңдеуді аламыз:

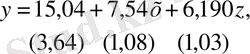
сондықтан, Уайт тесті 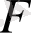- статистикасының

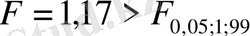
мәнін береді.

Уақыттық қатарлардағы регрессия модельдерінің өзгешеліктерін анықтау

Уақыттық қатарлар модельдеріндегі өзгешеліктердің дұрыс анықталмауы регрессия қателерінің автокорреляциялық себептері болуы мүмкін.

Келесі мысалды қарастырайық. X - жанұя кірісі (мың доллар), Y - шетелдерде демалуға жұмсалатын шығындар (мың доллар) болсын. Сурет 2 X және Y - шамаларының негізгі сандық сипаттамасы және жіктелу диаграммалары берілген.

Мұндағы X және Y - уақыттық қатарлар екенін ескере кету қажет, сондықтан жіктелу диаграммасынан басқа 10. 1 және 10. 2 кестелерінде келтірілген коррелограммаларда маңызды болып саналады.

Y шетелдегі демалуға жұмсалатын шығындардың Х кірістерден тәуелді болатын

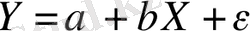(12. 24)

түріндегі модельді бағалайық. Ең кіші квадраттардың қарапайым әдісін қолдана отырып,

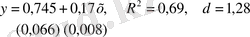
регрессия теңдеуін аламыз.

Дарбин - Уотсонның d статистикасы екі мәннен айтарлықтай ерекшеленуі регрессия қателерінің оң автокорреляциясының бар екендігін көрсетеді. Мүмкіндіктердің бірі - қалдықтар қатарын ARMA(p, g) модель қатары ретінде идентификациялау. Мұнда AR(1) ең қарапайым моделі адекватты болып табылады:

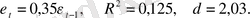
Бұл жолы Дарбин - Уотсонның d статистикасы екіге жуық екен. Осылайша, модель ретінде параметрлер мәнінің бағасынан тұратын

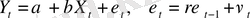
бірінші ретті авторегрессия моделін қабылдауымызға болады.

Алайда, шетелдегі курорттарда демалу сияқты - қымбат тауарлардың барлығы ағымдық кірістерден де, алдыңғы периодтағы кірістерден де тәуелді бола бермейді. Модель өзгешелігін анықтауды регрессорлар ретінде Х қадамды айнымалыларын қолдана отырып өзгертейік.

Төрт қадамды айнымалылар қосылған модель адекватты болып келеді. Регрессияның сәйкес теңдеуі келесі түрде болады:

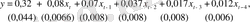
Көріп тұрғанымыздай, Дарбин - Уотсонның d статистикасының мәні екіге өте жуық, сондықтан жаңа модельде регрессия қателерінің автокорреляцияға қатысты мәселесі жоқ болады. Осыдан, оның себебі модель өзгешеліктерінің дұрыс анықталмауында екенін көруге болады. Сонымен қатар, 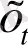жағдайында регрессия коэффициентінің екі есеге кемігенін көре аламыз.

Экономикалық талдаудың маңыздылығы

Модель өзгешелігін анықтауды таңдау барысындағы кез келген жағдайда ең алдымен экономикалық талдауға басшылық жасау қажет. Таңдалған мәліметтер - бұл тек қана цифрлар жиыны екенін ескеру керек және олармен күрделі іс-әрекеттер жасай отырып, кей жағдайда математикалық көзқарас бойынша төтенше жақсы модель алуға болады.

Мысал қарастырайық. Х - Бразилиядағы банан өңдеу өндірісі, Y - Ярославиялық машина дөңгелегін өндіру зауыты болсын. Осы шамалар "Уақыттық бақылаулар" графигінде бейнеленген.

Y -тің Х -тен тәуелді регрессиялық моделін қарастырайық және оны ең кіші квадраттардың қарапайым әдісімен бағалайық:

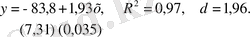
Математикалық көзқарас бойынша бұл модель барлық параметрлері бойынша өте ғажап болып есептелінеді. Сонымен қатар, мұндай нәтиженің экономикалық мағынасы да жоғары. Мұны қарапайым түрде түсіндіруге болады - қарастырылатын уақыт периодында екі шама да Х және Y арасындағы корреляцияның жоғары мәнін алуға болатын уақыттық трендке ие.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.