Комплекс айнымалы функциялар: Коши-Риман шарттары, туынды мен аналитикалық және гармоникалық функциялар, бейнелеу қасиеттері мен есептер


&4. Комплекс айнымалы дифференциал функция.
Коши - Риман шарты
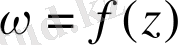 функциясы
функциясы
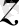 комплекс айнымалысының
комплекс айнымалысының
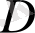 облысының кейбір нүктесінде анықталған болсын.
облысының кейбір нүктесінде анықталған болсын.
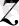 және
және
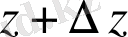 нүктелері
нүктелері
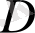 облысына жататын болсын. Бұдан
облысына жататын болсын. Бұдан
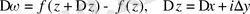 .
.
Анықтама 1.
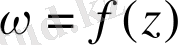 функциясы
функциясы
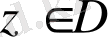 нүктесінде дифференциалданған
деп аталады, егер
нүктесінде дифференциалданған
деп аталады, егер
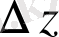 нүктесінде
нүктесінде
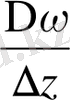 қатынасының соңғы шегі шартты түрде нөлге ұмтылатын болса. Бұл шек
қатынасының соңғы шегі шартты түрде нөлге ұмтылатын болса. Бұл шек
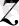 нүктесінде берілген
нүктесінде берілген
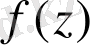 функцияның
туындысы
деп аталады және
функцияның
туындысы
деп аталады және
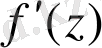 (немесе
(немесе
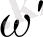 немесе
немесе
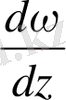 ) өрнегі арқылы белгіленеді, сондықтан анықтама бойынша
) өрнегі арқылы белгіленеді, сондықтан анықтама бойынша
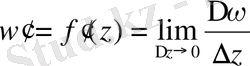 . (1)
. (1)
Егер
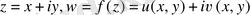 болса, онда әр нүктеде дифференциалданатын
болса, онда әр нүктеде дифференциалданатын
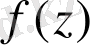 функциясы орындайтын қатынастарды
функциясы орындайтын қатынастарды
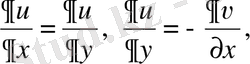 (2)
(2)
Коши - Риман шарты деп атайды.
Керісінше, егер
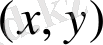 кейбір нүктелерінде
кейбір нүктелерінде
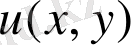 және
және
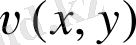 функциялары
функциялары
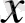 және
және
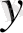 нақты айнымалылар сияқты дифференциалданатын, және сонымен қатар, (2) теңдікті қанағаттандыратын болса; онда
нақты айнымалылар сияқты дифференциалданатын, және сонымен қатар, (2) теңдікті қанағаттандыратын болса; онда
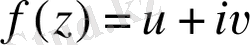 функциясы
функциясы
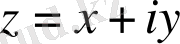 нүктесінде комплекс
нүктесінде комплекс
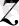 айнымалы функциясындай дифференциалданатын болады.
айнымалы функциясындай дифференциалданатын болады.
Анықтама 2.
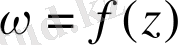 функциясы
функциясы
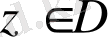 нүктесінде аналитикалық
деп аталады, егер
нүктесінде аналитикалық
деп аталады, егер
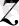 нүктесінде, сонымен қатар оның маңында дифференциалданатын болса.
нүктесінде, сонымен қатар оның маңында дифференциалданатын болса.
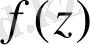 функциясы
функциясы
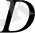 облысында
аналитикалық
деп аталады, егер ол осы облыстың әр нүктесінде дифференциалданатын болса. Кез келген аналитикалық
облысында
аналитикалық
деп аталады, егер ол осы облыстың әр нүктесінде дифференциалданатын болса. Кез келген аналитикалық
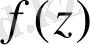 функциясы үшін
функциясы үшін
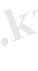
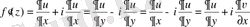 (3)
(3)
Мысал 1.
Комплекс жазықтығында
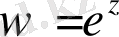 аналитикалық функция болатындығын көрсетіңіз.
аналитикалық функция болатындығын көрсетіңіз.
Шешімі.
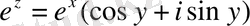 сондықтан да,
сондықтан да,
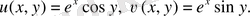
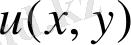 және
және
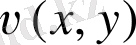 функциялары
функциялары
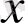 және
және
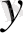 тұрақты айнымалы функциялар сияқты кез келген
тұрақты айнымалы функциялар сияқты кез келген
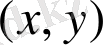 нүктесінде дифференциалданады (кез келген тәртіптегі үздіксіз жекеленген туындылары) және (2) шартты қанағаттанадырады.
нүктесінде дифференциалданады (кез келген тәртіптегі үздіксіз жекеленген туындылары) және (2) шартты қанағаттанадырады.
Демек,
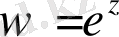 функциясы барлық жерде аналитикалық.
функциясы барлық жерде аналитикалық.
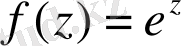 үшін (3) формуласына сәйкес мынаны аламыз:
үшін (3) формуласына сәйкес мынаны аламыз:
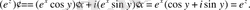
Осылайша,
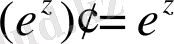 .
.
Мысал 2
.
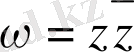 функциясы ең болмаса бір нүктеде аналитикалық бола ма?
функциясы ең болмаса бір нүктеде аналитикалық бола ма?
Шешімі.
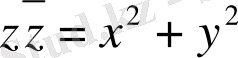 сондықтан да,
сондықтан да,
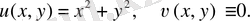
Коши - Риман шарты бұл жағдайда мына түрге ие
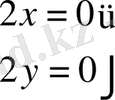
және
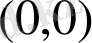 нүктесінде ғана қанағаттандырады.
нүктесінде ғана қанағаттандырады.
Демек,
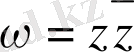 функциясы тек қана
функциясы тек қана
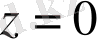 нүктесінде дифференциалданады және басқа еш жерде аналитикалық емес.
нүктесінде дифференциалданады және басқа еш жерде аналитикалық емес.
1 анықтаманы пайдаланып,
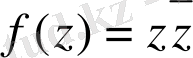 функциясы
функциясы
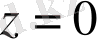 нүктесінде көрсетеміз. Шын мәнінде,
нүктесінде көрсетеміз. Шын мәнінде,
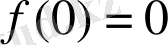 , сондықтан
, сондықтан
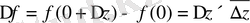
және
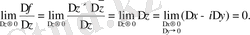
Осылайша,
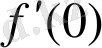 туындысы бар және ол нөлге тең.
туындысы бар және ол нөлге тең.
Мысал 3.
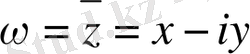 функциясы аналитикалық бола ма?
функциясы аналитикалық бола ма?
Шешімі.
Мұнда
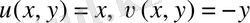 функциясы
функциясы
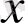 және
және
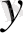 айнымалыларының барлық нүктесінде дифференциалданады. Әрі қарай,
айнымалыларының барлық нүктесінде дифференциалданады. Әрі қарай,
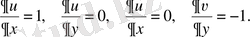
Сондықтан
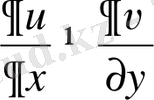 , яғни Коши - Риманның бірінші шарты комплекс жазықтығының бірде-біреуінде орындалмайды.
, яғни Коши - Риманның бірінші шарты комплекс жазықтығының бірде-біреуінде орындалмайды.
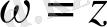 функциясы ешбір нүктеде дифференциалданбайды, демек, аналитикалық емес.
функциясы ешбір нүктеде дифференциалданбайды, демек, аналитикалық емес.
Коши - Риман шарттарын пайдаланып, келесі функциялардың қайсысы ең болмағанда бір нүктеде аналитикалық болатындығы, қайсысы болмайтындығын анықтау керек:
104.
а)
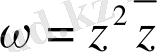 ; б)
; б)
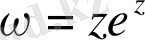 ; в)
; в)
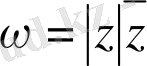 ; г)
; г)
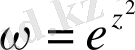 ; д)
; д)
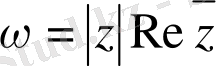 ; е)
; е)
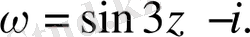
105.
а)
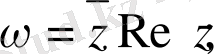 б)
б)
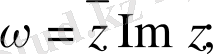 в)
в)
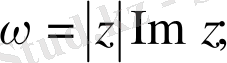 г)
г)
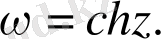
106.
 облысында
облысында
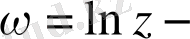 аналитикалық функция болатындығын көрсету керек.
аналитикалық функция болатындығын көрсету керек.
107.
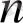 - натурал болғанда тікелей есептеуді көрсет:
- натурал болғанда тікелей есептеуді көрсет:
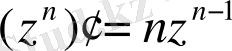 .
.
108.
Егер
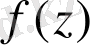 және
және
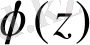 аналитикалық функциялар
аналитикалық функциялар
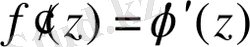 шартын қанағаттандыратын болса, онда
шартын қанағаттандыратын болса, онда
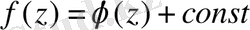 болатындығын көрсету керек.
болатындығын көрсету керек.
109.
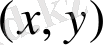 декарттық координат жүйесінен
декарттық координат жүйесінен
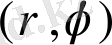 полярлыққа өту кезінде (2) Коши - Риман шарты мына түрге ие екенін көрсету керек:
полярлыққа өту кезінде (2) Коши - Риман шарты мына түрге ие екенін көрсету керек:
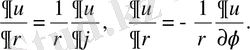 (4)
(4)
110.
Егер
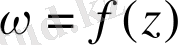 аналитикалық функциясы кейбір облыста анықталған болса, онда ол тұрақты болатынын көрсет.
аналитикалық функциясы кейбір облыста анықталған болса, онда ол тұрақты болатынын көрсет.
111.
Егер
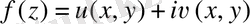 функциясы
функциясы
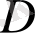 облысында аналитикалық болса, онда осы облыста мына теңдік орындалытындығын көрсет:
облысында аналитикалық болса, онда осы облыста мына теңдік орындалытындығын көрсет:
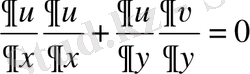 .
.
112.
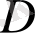 облысында
облысында
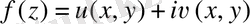 аналитикалық функция болсын.
аналитикалық функция болсын.
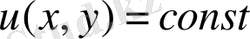 және
және
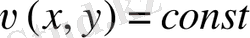 сызықтар жүйесі ортогоналды болатындығын көрсету керек.
сызықтар жүйесі ортогоналды болатындығын көрсету керек.
113. Аналитикалық функциясының модуль мен аргументі
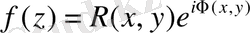
арақатынасымен байланысты
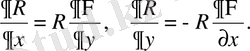
Коши - Риман шарттарын пайдаланп,
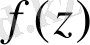 аналитикалық функциясын қалпына келтіруге болады, егер оның
аналитикалық функциясын қалпына келтіруге болады, егер оның
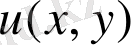 нақты бөлігі немесе
нақты бөлігі немесе
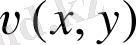 саналы бөлігі белгілі болса.
саналы бөлігі белгілі болса.
Сонымен қатар,
 нүктесінің маңында аналитикалық
нүктесінің маңында аналитикалық
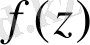 функциясын келесі формулалардың бірімен қалпына келтіруге болады:
функциясын келесі формулалардың бірімен қалпына келтіруге болады:
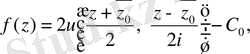 (5)
(5)
 (6)
(6)
мұндағы:
 нүктесінде
нүктесінде
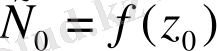 үшін
үшін
 - біріктірілген сан.
- біріктірілген сан.
Мысал 4.
Берілгені бойынша нақты
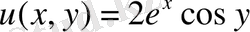 бөлігі және қосымша шарты
бөлігі және қосымша шарты
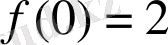 болатын
болатын
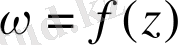 аналитикалық функциясын табу керек.
аналитикалық функциясын табу керек.
Шешімі:
Бірінші тәсіл.
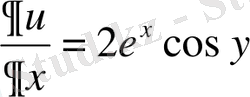 болсын. Коши - Риманның бірінші шарты бойынша
болсын. Коши - Риманның бірінші шарты бойынша
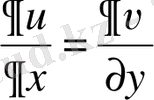 болуы керек, сондықтан
болуы керек, сондықтан
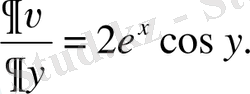 Бұдан
Бұдан
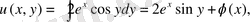 мұнда
мұнда
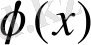 функциясы белгісіз.
функциясы белгісіз.
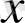 бойынша
бойынша
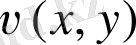 функциясын Коши - Риманның екінші шартын пайдаланып, дифференциалдасақ, мынаған келеміз
функциясын Коши - Риманның екінші шартын пайдаланып, дифференциалдасақ, мынаған келеміз
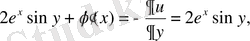
мұндағы
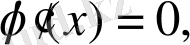 демек,
демек,
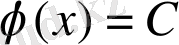 , мұндағы
, мұндағы
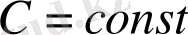 .
.
Осылайша,
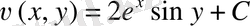 және бұдан
және бұдан
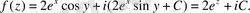
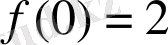 шартынан
шартынан
 тұрақтысын табамыз, яғни
тұрақтысын табамыз, яғни
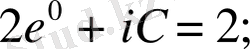 бұдан
бұдан
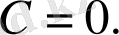 Жауабы:
Жауабы:
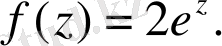
Екінші тәсіл. (5) формуланы қолданамыз. Бұл мысалда
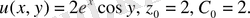 Демек, (5) формуласы бойынша
Демек, (5) формуласы бойынша
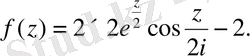
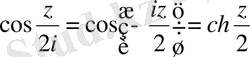 екендігін ескеріп, анық
екендігін ескеріп, анық
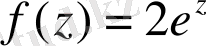 екендігін аламыз.
екендігін аламыз.
Мысал 5.
Шарт бойынша
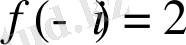 болғандағы саналы
болғандағы саналы
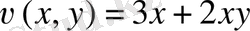 бөлігі арқылы
бөлігі арқылы
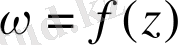 аналитикалық функциясын табу керек.
аналитикалық функциясын табу керек.
Шешімі: (6) формуланы пайдаланамыз. Бұл мысалда
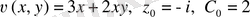 болғандықтан
болғандықтан
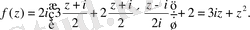
Белгілі
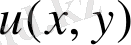 нақты бөлігі немесе саналы
нақты бөлігі немесе саналы
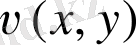 бөлігін және
бөлігін және
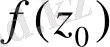 мағынасы арқылы
мағынасы арқылы
 нүктесінің маңында
нүктесінің маңында
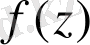 аналитикалық функциясын қалпына келтіру керек:
аналитикалық функциясын қалпына келтіру керек:
114.
a)
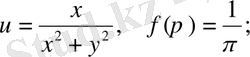
б)
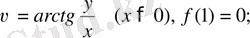
в)
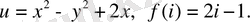
115.
а)
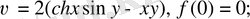
б)
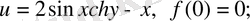
в)
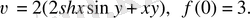
116.
а)
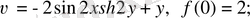
б)
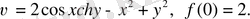
Анықтама 3.
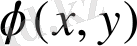 функциясы
функциясы
 облысында гармоникалық
деп аталады, егер ол осы облыста үздіксіз жеке туындылары екінші ретке дейін қамтылатын және қанағаттандырылатын осы облыстағы Лаплас теңдеуі мына түрде ие болса
облысында гармоникалық
деп аталады, егер ол осы облыста үздіксіз жеке туындылары екінші ретке дейін қамтылатын және қанағаттандырылатын осы облыстағы Лаплас теңдеуі мына түрде ие болса
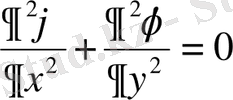 .
.
Егер
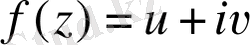 функциясы
функциясы
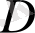 облысының кейбір бөлігінде аналитикалық болса, онда оның
облысының кейбір бөлігінде аналитикалық болса, онда оның
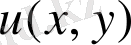 нақты бөлігі және
нақты бөлігі және
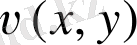 саналы бөлігі осы облыста гармоникалық функция болады.
саналы бөлігі осы облыста гармоникалық функция болады.
Бірақ, егер
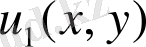 және
және
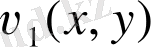 кез келген екі гармоникалық функция болса, онда
кез келген екі гармоникалық функция болса, онда
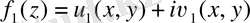 функциясы аналитикалық функция болуы міндетті емес:
функциясы аналитикалық функция болуы міндетті емес:
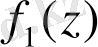 аналитикалық үшін
аналитикалық үшін
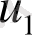 және
және
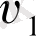 функциялары қосымша Коши - Риман шартын қанағаттандыру керек.
функциялары қосымша Коши - Риман шартын қанағаттандыру керек.
Гармоникалық екі функция (2) шартты қанағаттандырса, гармоникалық функцияның жіктелген жұбы (жұп функцияның реті сақталған) деп аталады.
117. Келесі функциялардың гармоникалық болатынын көрсету керек:
a)
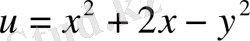 ;
;
б)
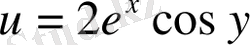 ;
;
в)
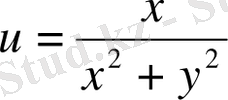 ;
;
г)
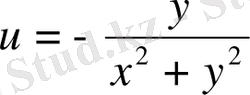 ;
;
д)
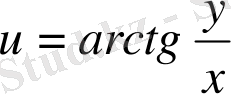 ;
;
е)
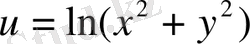 .
.
118.
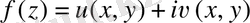 аналитикалық функциясының нақты және саналы бөлігі келесі функциялар бола ала ма:
аналитикалық функциясының нақты және саналы бөлігі келесі функциялар бола ала ма:
a)
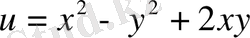 ;
;
б)
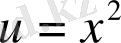 ;
;
в)
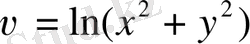 ;
;
г)
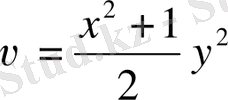 .
.
119.
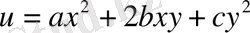 үшмүшесі қандай жағдайда гармоникалық функция болады?
үшмүшесі қандай жағдайда гармоникалық функция болады?
Келесі мысалдарда берілген
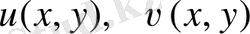 жұптары гармоникалық функциялар. Осылардың ішінен гармоникалық функцияның жіктелген жұбын тап.
жұптары гармоникалық функциялар. Осылардың ішінен гармоникалық функцияның жіктелген жұбын тап.
120.
а)
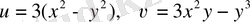 ;
;
б)
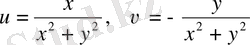 ;
;
в)
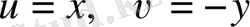 ;
;
г)
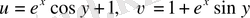 .
.
121.
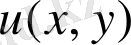 -
-
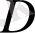 облысында гармоникалық функция болсын, оның үзіліссіз жеке туындысы кез келген ретте болсын.
облысында гармоникалық функция болсын, оның үзіліссіз жеке туындысы кез келген ретте болсын.
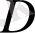 облысында соңғылары да гармоникалық функция болатындығын көрсету керек.
облысында соңғылары да гармоникалық функция болатындығын көрсету керек.
122.
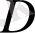 облысында
облысында
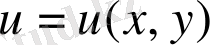 функциясы гармоникалық болсын.
функциясы гармоникалық болсын.
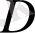 облысында
облысында
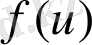 функциясы гармоникалық болатын барлық
функциясы гармоникалық болатын барлық
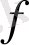 функциясын табу керек.
функциясын табу керек.
123.
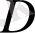 облысында
облысында
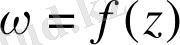 аналитикалық функция болсын.
аналитикалық функция болсын.
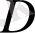 облысында
облысында
а)
 ; б)
; б)
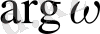 ; в)
; в)
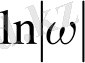
қай функция гармоникалық болады?
124.
 облысында гармоникалық көбейтіндінің жіктелуі
облысында гармоникалық көбейтіндінің жіктелуі
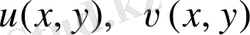 функцияларының
функцияларының
 облысында гармоникалық болатынын дәлелдеу керек.
облысында гармоникалық болатынын дәлелдеу керек.
125.
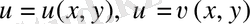 жіктелген жұп
жіктелген жұп
 облысында гармоникалық болсын.
облысында гармоникалық болсын.
 облысында келесі жұп функциялардың қайсысы жіктелген гармоникалық функция:
облысында келесі жұп функциялардың қайсысы жіктелген гармоникалық функция:
a)
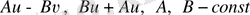 ;
;
б)
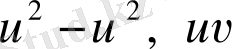 ;
;
в)
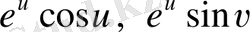 ?
?
Мысал 6.
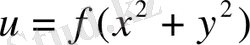 түріндегі тұрақты емес барлық гармоникалық функцияны табу керек.
түріндегі тұрақты емес барлық гармоникалық функцияны табу керек.
Шешімі. Ізделінді функция гармоникалық болуы қажет, өйткені олар мына Лаплас теңдеуін қанағаттандыруы тиіс
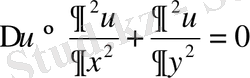 (7)
(7)
Берілген функцияны (7) теңдеумен ауыстырамыз. Бұл үшін оның екінші ретті туындысын табу қажет.
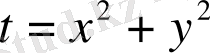 болсын. Онда
болсын. Онда
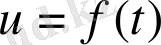 болады, мұндағы
болады, мұндағы
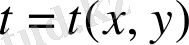 . Шарт бойынша күрделі функцияларды дифференциалдап, мынаған келеміз
. Шарт бойынша күрделі функцияларды дифференциалдап, мынаған келеміз
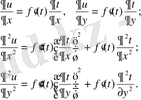
Соңғы екі теңдеуді қосу арқылы мынаған келеміз
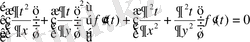
немесе
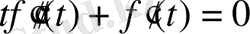 .
.
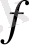 функциясын табу үшін Эйлер теңдеуін аламыз
функциясын табу үшін Эйлер теңдеуін аламыз
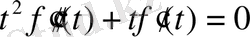
жалпы шешім мына функция
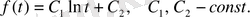
Осылайша, ізделінді гармоникалық функция мына түрге ие
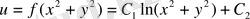 .
.
Келесі тапсырмаларда барлық көрсетілген түрлердің гармоникалық функцияларын табу керек:
126.
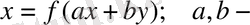 тұрақтылар.
тұрақтылар.
127.
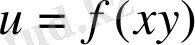
128.
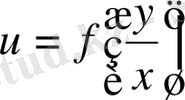 .
.
129.
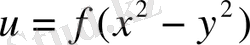 .
.
130.
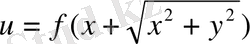 .
.
131.
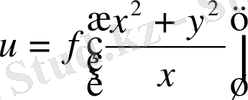 .
.
Модульдің геометриялық мағынасы және туындының дәлелдері
 нүктесінде
нүктесінде
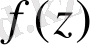 функциясы аналитикалық болсын және
функциясы аналитикалық болсын және
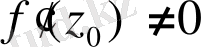 . Бұдан
. Бұдан
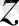 жазықтығынан
жазықтығынан
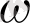 жазықтығына
жазықтығына
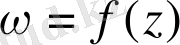 функциясын бейнелегенде
функциясын бейнелегенде
 нүктесінде
нүктесінде
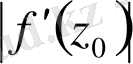 созылу коэффициентіне тең; дәлірек айтқанда:
созылу коэффициентіне тең; дәлірек айтқанда:
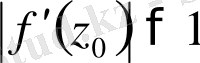 кезінде созылу,
кезінде созылу,
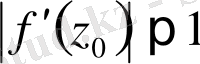 - қысылу болады.
- қысылу болады.
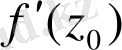 геометриялық туындының дәлелдері бұрышқа тең,
геометриялық туындының дәлелдері бұрышқа тең,
 нүктесін,
нүктесін,
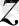 кез келген тегіс қисыққа қатысты бұру қажет, нүктеге
кез келген тегіс қисыққа қатысты бұру қажет, нүктеге
 нүктесі арқылы өтетін
нүктесі арқылы өтетін
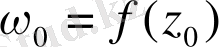 тәуелді бағыт алу үшін
тәуелді бағыт алу үшін
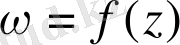 бейнелеген кезде бұл қисықтың кескініне
бейнелеген кезде бұл қисықтың кескініне
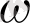 . Егер
. Егер
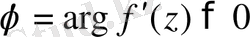 болса, онда бұрылу сағат тіліне қарама-қарсы өтетінін ескерсек,
болса, онда бұрылу сағат тіліне қарама-қарсы өтетінін ескерсек,
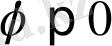 сағат тілімен бағыттас.
сағат тілімен бағыттас.
Мысал 7.
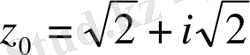 нүктесінде
нүктесінде
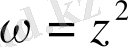 бейнелеуінде созылу коэффициентін және бұрылу бұрышын табу қажет.
бейнелеуінде созылу коэффициентін және бұрылу бұрышын табу қажет.
Шешімі.
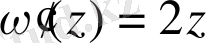 болса, онда
болса, онда
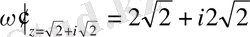 .
.
Күрделі санның алгебралық формасынан
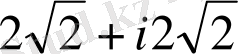 тригонометриялық түрге өтуінен мынаған келеміз
тригонометриялық түрге өтуінен мынаған келеміз
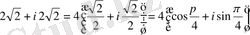 .
.
Бұдан,
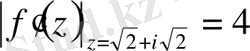
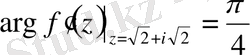 ,
,
демек созылу коэффициенті
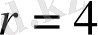 , ал бұрылу бұрышы
, ал бұрылу бұрышы
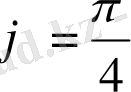 .
.
Берілген нүктеде берілген
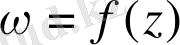 кескіндері үшін
кескіндері үшін
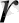 созылу коэффициенті мен
созылу коэффициенті мен
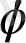 бұрылу бұрышын табу қажет:
бұрылу бұрышын табу қажет:
132.
a)
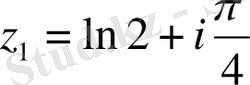 және
және
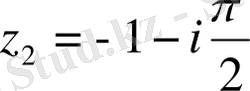 нүктелерінде
нүктелерінде
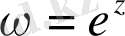 ;
;
б)
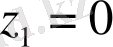 және
және
 нүктелерінде
нүктелерінде
 ;
;
в)
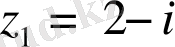 және
және
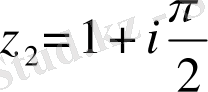 нүктелерінде
нүктелерінде
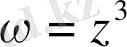 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz