Көрсеткіштік, логарифмдік және тригонометриялық теңсіздіктер: теория, шешу әдістері, мысалдар мен тест тапсырмалары


Мазмұны
- Көрсеткіштік теңсіздіктерТеориялық сұрақтарТест-тапсырмаларБақылау тапсырмаларыҰлттық бірыңғай тестілеуде берілген тапсырмаларЖауабы
- Логарифмдік теңсіздіктерТеориялық сұрақтарТест-тапсырмаларБақылау тапсырмаларыҰлттық бірыңғай тестілеуде берілген тапсырмаларЖауабы
- Тригонометриялық теңсіздіктерТеориялық сұрақтарТест-тапсырмаларБақылау тапсырмаларыҰлттық бірыңғай тестілеуде берілген тапсырмаларЖауабы
- Кері тригонометриялық функциялары бар теңсіздіктерТеориялық сұрақтарТест-тапсырмаларБақылау тапсырмаларыЖауабы
§1 Көрсеткіштік теңсіздіктер
Көрсеткіштік теңсіздіктің түрлері мен оларды шешу тәсілдерін қарастырудан бұрын ең алдымен көрсеткіштік функциялардың қасиеттерін, көрсеткіштік теңдеулердің қарапайым түрлерін шешу тәсілдерін білу қажет.
Көрсеткіштік теңсіздіктерді шешу тәсілдері негізінен көрсеткіштік теңдеулерді шешудің әдіс амалдарымен сабақтасып жатады.
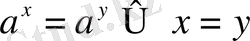
тұжырымдамасына сүйеніп, көрсеткіштік теңсіздіктерде де негізін түсіріп жазуға болады, бірақ
1° егер
 және
және
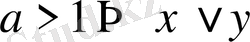 ;
;
2° егер
 және
және
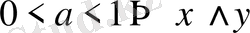
болады, мұндағы ∨ белгісі >, <, ≥, ≤ төрт белгінің біреуі ретінде түсінеміз деп айтылған.
Ал ∧ белгісі берілген белгіге қарама-қарсы белгі деген сөз. Демек, көрсеткіштік теңсіздіктегі өрнектердің негіздері бірдей болса, негіздерін түсіріп жазуға болады, бірақ негізі бірден үлкен болса, теңсіздік мағынасы сақталынады.
Ал негізі бірден кіші болса, қарама-қарсыға өзгереді.
Мысалы.
1)
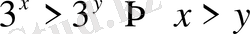 себебі негізі бірден үлкен
себебі негізі бірден үлкен
болады
2)
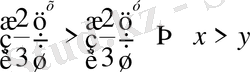 себебі негізі бірден
себебі негізі бірден
кіші сан.
Бұл тақырыпты талдауды көрсеткіштік теңсіздіктердің қарапайым дербес түрлерін шешуден бастайық:
І
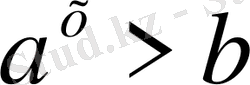 (≥) түрлеріндегі теңсіздік,
мұнда
а
>0 және
а
≠1 (үлкен және кіші емес (≥) екі жағдайды бірдей қарастырамыз) :
(≥) түрлеріндегі теңсіздік,
мұнда
а
>0 және
а
≠1 (үлкен және кіші емес (≥) екі жағдайды бірдей қарастырамыз) :
1) Егер
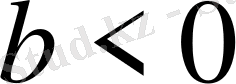 немесе
немесе
 болса, онда теңсіздіктің шешімі кез келген сан болады яғни
х
∈R;
болса, онда теңсіздіктің шешімі кез келген сан болады яғни
х
∈R;
2) Егер
 болса, онда
b
-ның қабылдайтын мәндеріне байланысты және негізіне байланысты бірнеше дербес жағдайларына тоқталайық:
болса, онда
b
-ның қабылдайтын мәндеріне байланысты және негізіне байланысты бірнеше дербес жағдайларына тоқталайық:
а)
 және
және
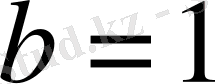 болсын, онда
болсын, онда
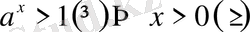 ;
;
б)
 және
және
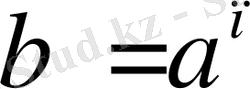 болсын, онда
болсын, онда
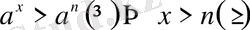 ;
;
в)
 және
b
кез келген сан, онда
және
b
кез келген сан, онда
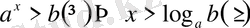 ;
;
г)
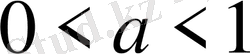 және
және
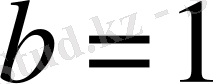 болсын, онда
болсын, онда
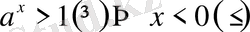 ;
;
д)
 және
және
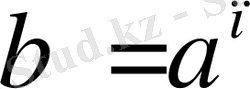 болса, онда
болса, онда
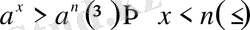 ;
;
е)
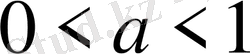 және кез келген
b
саны үшін
және кез келген
b
саны үшін
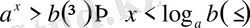 болады.
болады.
Демек көрсеткіштік өрнектің негізі бірден үлкен болса, негізін түсіргенде теңсіздік мағынасы сақталынады, ал негізі бірден кіші болса, онда теңсіздік мағынасы қарама-қарсыға өзгеретіндігін үнемі есте ұстаған жөн.
Мысалдар. Теңсіздіктерді шешіңіз
1)
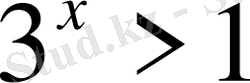
Шығарылуы. а =3 негізі бірден үлкен b =1, демек х >0.
2)

Шығарылуы. b =-9 теріс сан, демек х ∈R .
3)
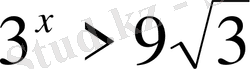
Шығарылуы.
а
=3,
b
=
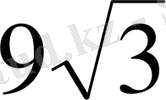 бірақ, ол да 3-негізіне келтірімді
бірақ, ол да 3-негізіне келтірімді
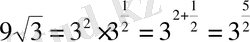 ,
,
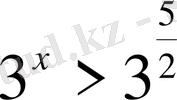 =>
=>
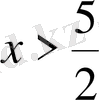 .
.
4)
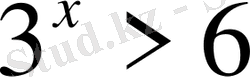
Шығарылуы.
а
=3,
b
=6 бірақ, 6 саны 3 негізіне келтірілмейді, демек
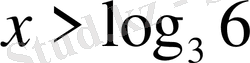 .
.
5)
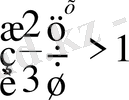
Шығарылуы.
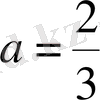 ,
b
=1 негізі бірден кіші
х
<0.
,
b
=1 негізі бірден кіші
х
<0.
6)
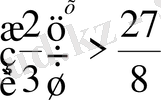
Шығарылуы.
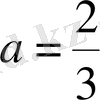 ,
,
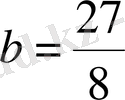 , негіздерін бірдей түрге келтіріміз
, негіздерін бірдей түрге келтіріміз
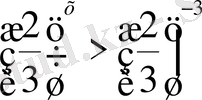 , негіздері бірден кіші,
х
<-3.
, негіздері бірден кіші,
х
<-3.
7)
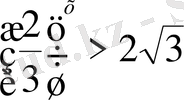
Шығарылуы.
Сандық шамалары ұқсас болғанымен бірдей негізге келтірілмейді, демек жауап логарифм арқылы өрнектеледі
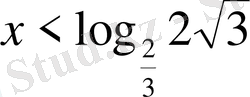 .
.
8)
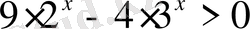
Шығарылуы.
Көрсеткіштік өрнектердің негіздері әртүрлі, бірақ
 екенін ескерсек теңсіздіктің екі жағын да
екенін ескерсек теңсіздіктің екі жағын да
 бөлеміз.
бөлеміз.
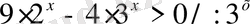
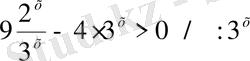
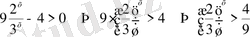
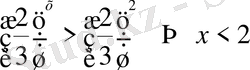
Біз жоғарыдағы мысалдарда тек үлкен (>) жағдайын қарастырдық, дәл осы санды кіші емес (≥) жағдайы да есептелінеді.
Мысалы. Теңсіздікті шешіңіз
9)
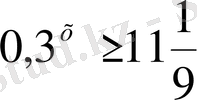
Шығарылуы.
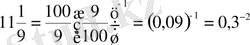 .
.
Демек
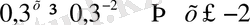 .
.
10)
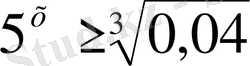
Шығарылуы.
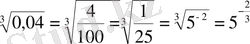 .
.
Демек
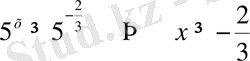 .
.
11)
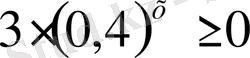
Шығарылуы. Теңсіздіктің екі жағында 3-ке қысқартамыз.
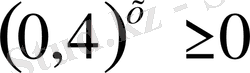 , яғни
, яғни
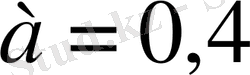 ,
b
=0, бұдан шешім кез келген сан деген қортындыға келеміз.
,
b
=0, бұдан шешім кез келген сан деген қортындыға келеміз.
Табылған теңсіздіктер шешімдерінің дұрыстығына көз жеткізу үшін, қарастырылып отырған аралықтан кез келген санды айнымалының орнына қойғанда, дұрыс мағыналы сандық теңсіздік алыныды.
Мысалы.
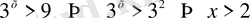
2-ден үлкен кез келген сан теңсіздікті қанағаттандырады
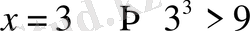 немесе
немесе
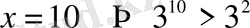
керісінше х =2 немесе одан кіші сан болса, онда теңсіздік мағынасы болмайды.
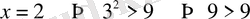 олай болуы мүмкін емес.
олай болуы мүмкін емес.
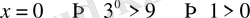 бұрыс теңсіздік.
бұрыс теңсіздік.
II
 (≤) түріндегі теңсіздік (
а
>0,
а
≠1)
(≤) түріндегі теңсіздік (
а
>0,
а
≠1)
Бұл түрдегі теңсіздік (I) түрдегімен қарама-қарсы мағынада болғандықтан, шешім де қарама-қарсы мағынада жазылады.
- Егерb<0 немесеb=0 болса, онда теңсіздіктің шешімі болмайды.
- Егерb>0, ал көрсеткіштік өрнектің негізі бірден үлкен болса, негіздері түсірілгенде теңсіздік мағынасы сақталынады, негізі бірден кіші болса, негіздері түсірілгенде таңба қарама-қарсыға өзгеруіне сүйенеміз.
11)
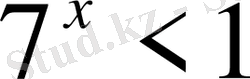
Шығарылуы. а =7, b =1 => х >0.
12)
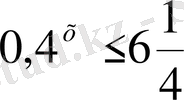
Шығарылуы.
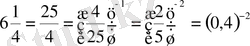
 .
.
13)
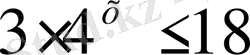
Шығарылуы.
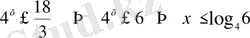 .
.
14)
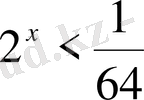
Шығарылуы
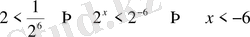 .
.
III
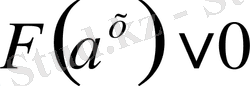 немесе
немесе
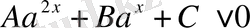 түріндегі теңсіздіктер,
түріндегі теңсіздіктер,
 деп белгілеп жаңа айнымалы енгізу арқылы қарапайым стандартты түрдегі теңсіздіктерге келтіріледі.
деп белгілеп жаңа айнымалы енгізу арқылы қарапайым стандартты түрдегі теңсіздіктерге келтіріледі.
Мысалы. Теңсіздіктерді шешіңіз
15)
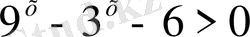
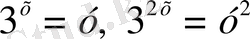 деп белгілеп,
деп белгілеп,
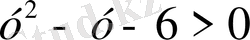 квадрат теңсіздігін аламыз.
квадрат теңсіздігін аламыз.
D
=25,
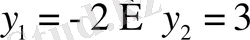 онда оның шешімі
онда оның шешімі
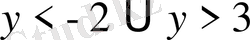 арқылы өрнектелінеді.
арқылы өрнектелінеді.
Бастапқы айнымалаға қайта көшсек,
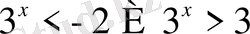 . Бірінші теңсіздіктің шешімі жоқ, екіншіде
х
>1.
. Бірінші теңсіздіктің шешімі жоқ, екіншіде
х
>1.
Жауап: (1; +∞) .
16)
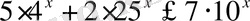
Шығарылуы.
Көрсеткіштік өрнек 4, 25, 10 үш түрлі негізде берілген, сондықтан бір негізге келтіру үшін, теңсіздіктің екі жағын да
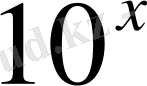 -бөлеміз. Нәтижесінде
-бөлеміз. Нәтижесінде
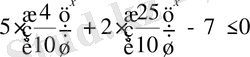 теңсіздігінен
теңсіздігінен
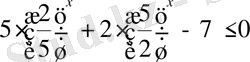 аламыз.
аламыз.
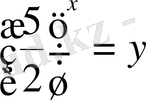 деп белгілесек,
деп белгілесек,
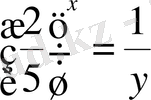 болады.
болады.
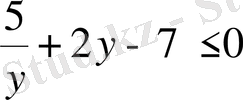 ,
,
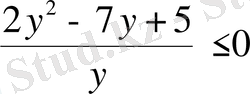 .
.
Бөлшек бөлімі әрқашанда оң мәнді екенін ескеріп
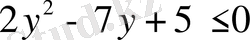 теңсіздігін аламыз.
теңсіздігін аламыз.
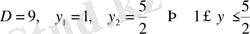 у
айнымалысын бастапқы өрнекпен қайта алмастырсақ
у
айнымалысын бастапқы өрнекпен қайта алмастырсақ
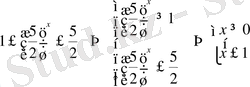 .
.
Жауап
 .
.
17) Теңсіздікті шешіңіз
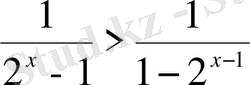
Шығарылуы.
 деп белгілесек
деп белгілесек
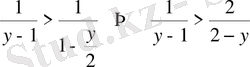 теңсіздігін аламыз.
теңсіздігін аламыз.
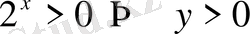 екенін ескеріп, теңсіздіктер жүйесін аламыз
екенін ескеріп, теңсіздіктер жүйесін аламыз
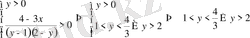
Бастапқы айнымалыға қайта көшсек
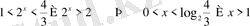 .
.
Жауап
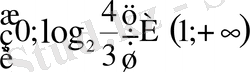 .
.
IV
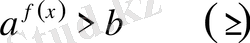 түріндегі теңсіздік
түріндегі теңсіздік
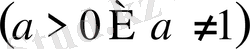 ,
мұндағы
,
мұндағы
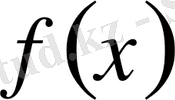 кез келген рационал функция.
кез келген рационал функция.
- Егернемесеболса, онда тесңсіздіктің шешіміфункциясының анықталу облысымен сәйкес келеді.
- Егерболса, көрсеткіштік өрнектің негізіне баса назар аударамыз
а)
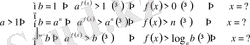
б)
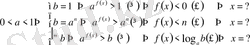
Мысалдар . Теңсіздіктерді шешіңіз
17)
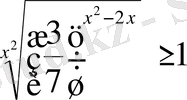
Шығарылуы.
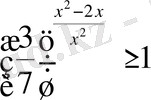 негізі бірден кіші, демек негіздерін түсіріп жазғанда теңсіздік таңбасы қарама-қарсыға өзгереді
негізі бірден кіші, демек негіздерін түсіріп жазғанда теңсіздік таңбасы қарама-қарсыға өзгереді
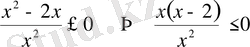 .
.
Аралықтар тәсілі арқылы шешімін жазамыз. Жауап
 .
.
18)
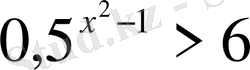
Шығарылуы.
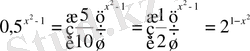
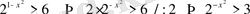
2 мен 3 бірдей негізге келтірілмейді, демек 2 негізінде логарифмдейміз
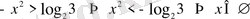 .
.
19) а)
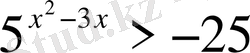
Шығарылуы.
Теңсіздіктің оң жағы теріс сан. Демек, шешім
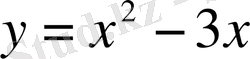 функциясының анықталу облысымен сәйкес келеді.
функциясының анықталу облысымен сәйкес келеді.
б)
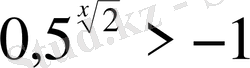
Шығарылуы.
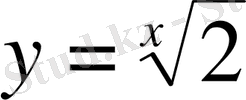 функциясының анықталу облысы
функциясының анықталу облысы
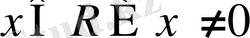 .
.
в)
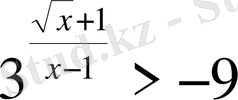
Шығарылуы.
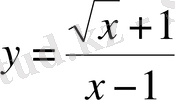 функциясының анықталу облысы
функциясының анықталу облысы
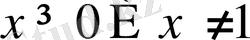 .
.
Жауап
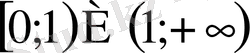 .
.
V
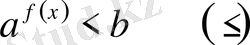 түріндегі теңсіздіктер
кез келген рационал функция.
түріндегі теңсіздіктер
кез келген рационал функция.
1) Егер
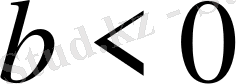 немесе
немесе
 болса, онда теңсіздіктің шешімі болмайды.
болса, онда теңсіздіктің шешімі болмайды.
2) Егер
 болса, көрсеткіштік өрнектің негізіне баса назар аударамыз.
болса, көрсеткіштік өрнектің негізіне баса назар аударамыз.
а)
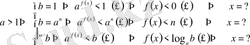
б)
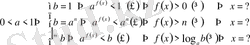
Мысалдар. Теңсіздіктерді шешіңіздер
20)
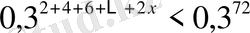
Шығарылуы.
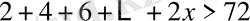 теңсіздіктің сол жағындағы қосынды арифметикалық прогрессияның мүшелерінің қосындысын береді.
теңсіздіктің сол жағындағы қосынды арифметикалық прогрессияның мүшелерінің қосындысын береді.
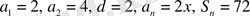 .
.
Бұдан
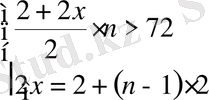 жүйені аламыз.
жүйені аламыз.
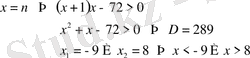
Прогрессия мүшелерінің саны оң санмен өрнектелінетіндіктен жауап
 .
.
21)
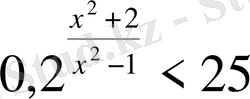
Шығарылуы.
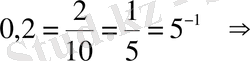
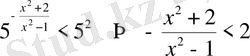
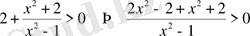
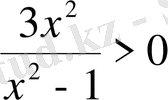 . Жауап
. Жауап
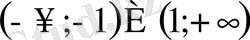 .
.
VІ
 түріндегі теңсіздіктер
түріндегі теңсіздіктер
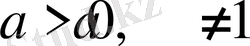 және
және
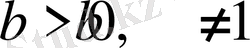 мұндағы
мұндағы
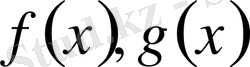 - рационал функциялар.
- рационал функциялар.
1) а мен в сандары бірдей негізге келтірілетін болса, келтіріп, негіздерін түсіріп жазамыз
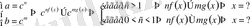 Мысал.
Теңсіздікті шешіңіз
Мысал.
Теңсіздікті шешіңіз
22)
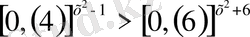
Шығарылуы. Негіздері әртүрлі, сондықтан түрлендіріп бірдей түрге келтіруге тырысамыз. Екіншіден 0, (4) және 0, (6) периодты ондық бөлшектер, демек
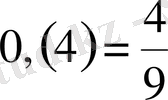 және
және
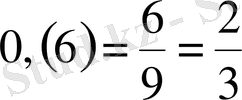 .
.
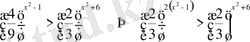 .
.
Өрнектердің негіздері бірдей және бірден кіші болғандықтан негіздерін түсіріп, теңсіздік таңбасын қарама-қарсыға өзгертіп жазамыз
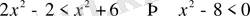 .
.
Жауап
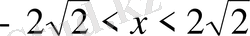 .
.
23)
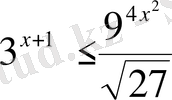
Шығарылуы.
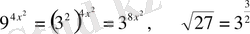
нәтижесінде
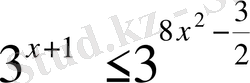 . Негізі бірден үлкен, демек негіздерін түсіріп жазғанда, теңсіздік мағынасы сақталынды
. Негізі бірден үлкен, демек негіздерін түсіріп жазғанда, теңсіздік мағынасы сақталынды
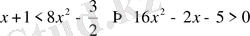 ,
,
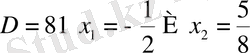 .
.
Жауап
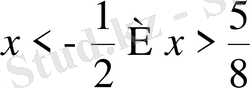 .
.
VІІ
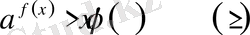 түріндегі теңсіздік,
мұндағы
түріндегі теңсіздік,
мұндағы
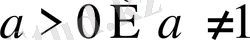 ,
,
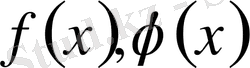 кез келген элементар функциялар.
кез келген элементар функциялар.
Бұл тұрғыдағы теңсіздіктерді шешу үшін көрсеткіштік функцияның қасиеттеріне сүйеніп, зерттеулер жүргіземіз.
1)
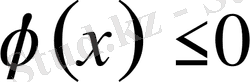 онда бастапқы теңсіздік шешімі
онда бастапқы теңсіздік шешімі
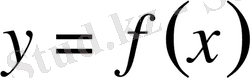 функциясының анықталу облысының қиылысуы болады.
функциясының анықталу облысының қиылысуы болады.
2)
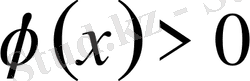 онда, көрсеткіштік өрнектің негізіне тәуелді теңсіздік аламыз және
онда, көрсеткіштік өрнектің негізіне тәуелді теңсіздік аламыз және
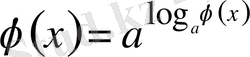 теңдігімен алмастырамыз. Нәтижесінде
теңдігімен алмастырамыз. Нәтижесінде
егер
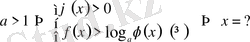
егер
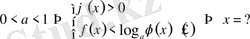
теңсіздіктер жүйесін шешеміз.
Мысалы . Теңсіздікті шешіңіз
24)
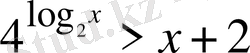
Шығарылуы.
1)
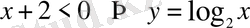 функциясының анықталу облысы
функциясының анықталу облысы
 , демек
, демек
 .
.
2)
 болсын, онда
болсын, онда
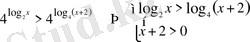
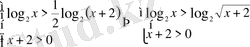
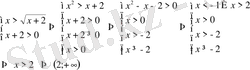 Жауап
Жауап
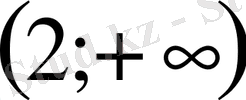 .
.
2-тәсіл.
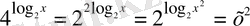 екенін ескерсек, берілген теңсіздік
екенін ескерсек, берілген теңсіздік
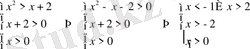 теңсіздіктер жүйесінің шешімі
теңсіздіктер жүйесінің шешімі
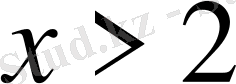 .
.
VІІІ
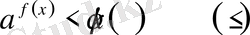 түріндегі теңсіздіктер.
Бұл жағдайда
түріндегі теңсіздіктер.
Бұл жағдайда
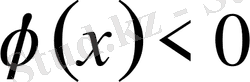 болуы мүмкін емес, себебі шешім болмайды. Демек теңсіздік
болуы мүмкін емес, себебі шешім болмайды. Демек теңсіздік
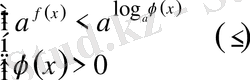 теңсіздіктер жүйесіне келтіріледі.
теңсіздіктер жүйесіне келтіріледі.
Мысал . Теңсіздікті шешіңіз
25)
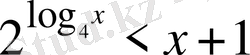
Шығарылуы.
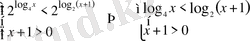
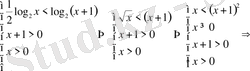
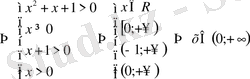
ІХ
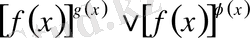 түріндегі теңсіздіктер,
мұнда
түріндегі теңсіздіктер,
мұнда
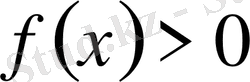 және
және
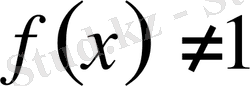 .
.
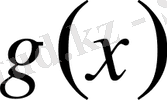 және
және
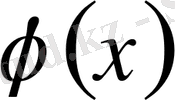 кез келген элементар функциялар. Бұл түрдегі теңсіздіктер төменгі екі системаға жіктелінеді.
кез келген элементар функциялар. Бұл түрдегі теңсіздіктер төменгі екі системаға жіктелінеді.
1)
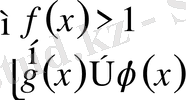 және 2)
және 2)
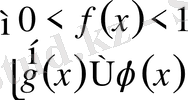
осы жүйелердің шешімі бастапқы теңсіздіктің шешімі болады.
Мысалдар. Теңсіздіктерді шешіңіз
26)
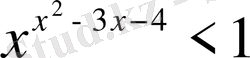
Шығарылуы.
1)
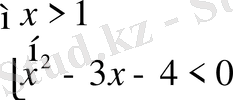 және 2)
және 2)
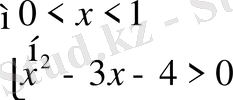
Әрбір жүйені жеке-жеке шешеміз:
1)
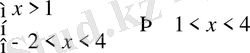 ;
;
2)
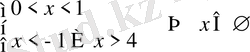 .
.
Жауап
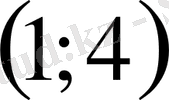 .
.
27)
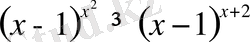
Шығарылуы.
1)
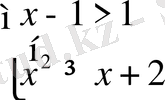 және 2)
және 2)
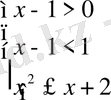 .
.
Әрбір жүйені жеке-жеке шешеміз
1)
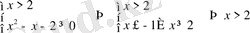 ;
;
2)
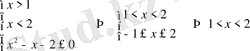 .
.
Жауап
 .
.
Көрсеткіштік теңсіздіктерді шешуде оларды түрлендіріп, стнадартты түрге келтірумен қатар, басқа да әдіс-тәсілдерді қолдана білген тиімді:
а) аралықтар тәсілі:
Берілген трансценденттік өрнектерді теңсіздіктің бір жағына шығарып, көбейткіштерге жіктейміз.
Әрбір көбейткішті нольге теңестіру арқылы, берілген теңсіздіктің анықталу облысындағы нольдерін тауып, сол нүктелер арқылы анықталу облысын белгілі бір аралықтарға бөлеміз. Әрбір аралықта өрнектің таңбасын анықтаймыз. Таңбалар қисығын жүргіземіз. Тапсырма шартына сәйкес қажетті аралықты, штрихтау арқылы белгілеп, жауабын анықтаймыз.
Мысалы. Теңсіздікті шешіңіз
28)
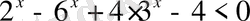
Шығырылуы.
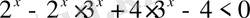
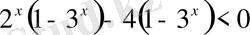
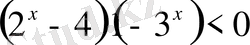 .
.
Демек
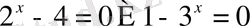
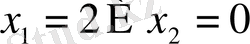

Жауап
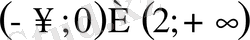 .
.
29) Теңсіздікті шешіңіз
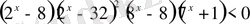
Шығарылуы.
Әрбір көбейткішті нөлге теңестіру арқылы, өрнектің мәндерін табамыз. Олар
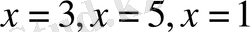 . Демек, сан өсі
. Демек, сан өсі
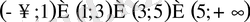 аралықтарына бөлінеді. Әрбір аралықта өрнектің таңбасын анықтаймыз, яғни
аралықтарына бөлінеді. Әрбір аралықта өрнектің таңбасын анықтаймыз, яғни

Жауап
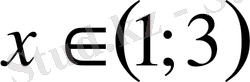 .
.
б) графиктік тәсіл:
Қайсыбір жағдайларда бұл тәсілдің тиімділігі айқын сезіледі. Ол үшін координаталар жазықтығына теңсіздіктегі қарапайым функциялардың графиктерін салып, олардың қисықтары бойындағы теңсіздік шартын қанағаттандыратын нүктелер жиынын, жауап ретінде көрсетеміз.
Мысалы. Теңсіздікті шешіңіз
30)
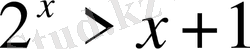
Шығарылуы.
Координаталар жазықтығына
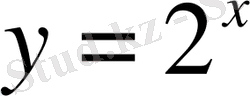 және
және
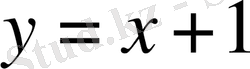 функцияларының графиктерін саламыз
функцияларының графиктерін саламыз
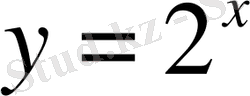
2 - сурет
Бұдан байқағанымыз
 нүктесінен басқа абциссаның барлық мәндері үшін
нүктесінен басқа абциссаның барлық мәндері үшін
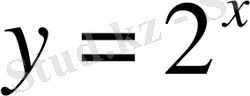 функциясының графигі
функциясының графигі
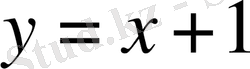 функциясының графигінен жоғары орналасқан. Демек
функциясының графигінен жоғары орналасқан. Демек
 нүктесінен басқа барлық нүктелер теңсіздік шешімі болады. Жауап
нүктесінен басқа барлық нүктелер теңсіздік шешімі болады. Жауап
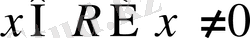 .
.
31) Теңсіздікті шешіңіз
 .
.
Шығарылуы.
Көрсеткіштік теңдеулер тақырыбындағы бірінші суреттегі
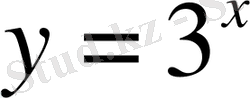 және
және
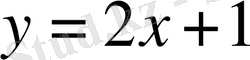 функциялар графиктерінің орналасуына назар аударсақ,
функциялар графиктерінің орналасуына назар аударсақ,
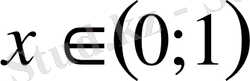 аралығында ғана
аралығында ғана
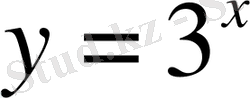 функциясының графигі
функциясының графигі
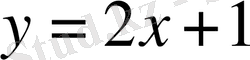 түзуінен төмен орналасады. Демек жауап
түзуінен төмен орналасады. Демек жауап
 .
.
1. 1 Қайталауға арналған сұрақтар
- Көрсеткіштік теңдеулер мен теңсіздіктерді шешуде қандай сабақтастық бар?
- Қарапайым түрдегі көрсеткіштік теңсіздіктер қалай шешіледі?
- Қандай жағдайларда көрсеткіштік теңсіздіктерге жаңа айнымалы енгізу керек?
- Негіздері бірдей түрге келтірілмесе көрсеткіштік теңсіздікті қалай шешуге болады?
- жәнетеңсіздіктерін шешу тәсілдерінде қандай айырмашылықтар бар?
- түріндегі теңсіздіктердегі- функциялары қандай шарттарды қанағаттандыруы керек.
- теңсіздігіндеболса теңсіздік шешімі қалай табылады?
- Көрсеткіштік теңсіздіктерді графиктік тәсілдер мен шешу алгоритімін еске түсіріңіз.
- Көрсеткіштік теңсіздіктердің шешімдерінің дұрыс, бұрыс табылғандығын қалай тексеруге болады?
- Біртекті көрсеткіштік теңсіздіктерді шешу тәсілдерін айтыңыз.
- а- параметрінің қандай шешіміинтервалы болады?
- теңсіздігінің кез келгенпсаны үшін орындалатынын дәлелдеңіз.
1. 2 Тест тапсырмалар
- Теңсіздікті шешіңіз
А)
 В)
В)
 С)
С)
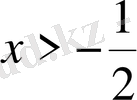 D)
D)
 Е)
Е)

- Теңсіздікті шешіңіз
А)
 В)
В)
 С)
С)
 D)
D)
 Е)
Е)
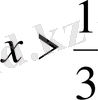
- Теңсіздікті шешіңіз
А)
 В)
В)
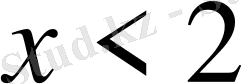 С)
С)
 D)
D)
 Е)
Е)

- Теңсіздікті шешіңіз
А)
 В)
В)
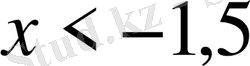 С)
С)
 D)
D)
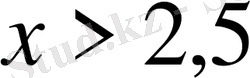 Е)
Е)

- Теңсіздікті шешіңіз
А)
 В)
В)
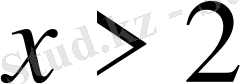 С)
С)
 D)
D)
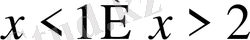 Е)
Е)

- Теңсіздікті шешіңіз
А)
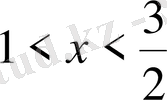 В)
В)
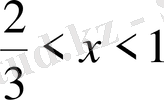 С)
С)
 D)
D)
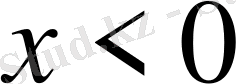 Е)
Е)

- Теңсіздікті шешіңіз
А)
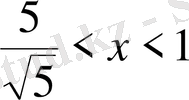 В)
В)
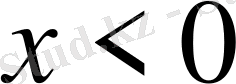 С)
С)
 D)
D)
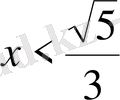 Е)
Е)

- Теңсіздікті шешіңіз
А)
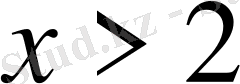 В)
В)
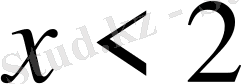 С)
С)
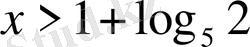 D)
D)
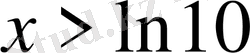 Е)
Е)
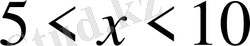
- Теңсіздікті шешіңіз
А)
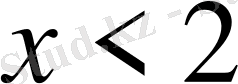 В)
В)
 С)
С)
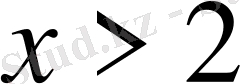 D)
D)
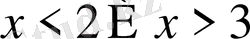 Е)
Е)
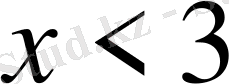
- теңсіздігін шешкенде төмендегі тәсілдердің қайсысын пайдаланған тиімді
А) графиктік В) аралықтар
С) жаңа айнымалы енгізіп, ықшамдаймыз
D)
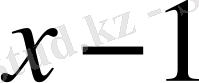 өрнегіне теңсіздіктің екі жағын да бөлу арқылы
өрнегіне теңсіздіктің екі жағын да бөлу арқылы
Е)
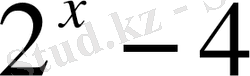 өрнегіне теңсіздіктің екі жағын да бөлу арқылы
өрнегіне теңсіздіктің екі жағын да бөлу арқылы
- теңсіздігін шешкенде төмендегі тәсілдердің қайсысымен шығарған тиімді
А) негіздерін түсіріп, сызықты теңсіздікке келтіру нәтижесінде
В) ұқсас мүшелерін біріктіріп, стандартты түрге келтіру
С) жаңа айнымалы енгізу арқылы квадрат теңсіздікке келтіреміз
D) 2-ге бөліп жібереміз
Е) 2 - негізде логарифмдейміз
- Теңсіздікті шешіңіз
А)
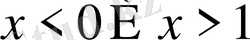 В)
В)
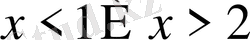 С)
С)
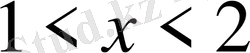
D)
 Е)
Е)

- Теңсіздікті шешіңіз
А)
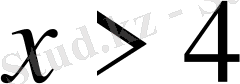 В)
В)
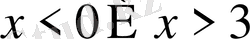 С)
С)
 D)
D)
 Е)
Е)

- Теңсіздікті шешіңіз
А)
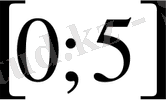 В)
В)
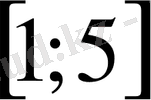 С)
С)
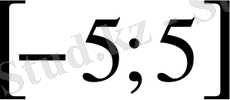 D)
D)
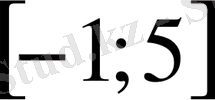 Е)
Е)
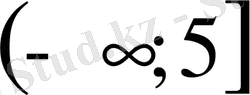
- Теңсіздікті шешіңіз
А)
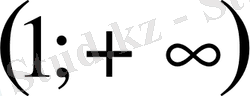 В)
В)
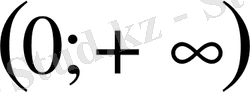 С)
С)
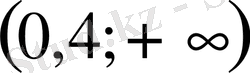
D)
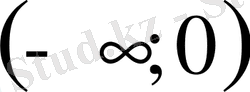 Е)
Е)
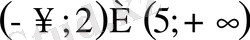
- Теңсіздікті шешіңіз
А)
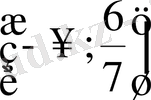 В)
В)
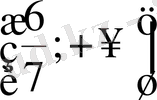 С)
С)
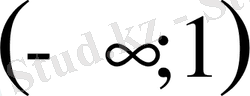 D)
D)
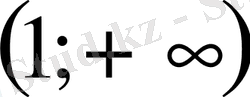 Е)
Е)
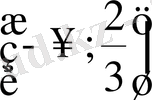
- Теңсіздікті шешіңіз
А)
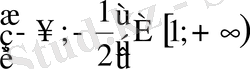 В)
В)
 С)
С)
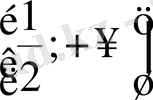
D)
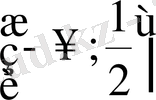 Е)
Е)
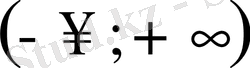
- теңсіздігін төмендегі сандардың қайсысы қанағаттандырады
А) 1 В)
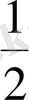 С) 2 D) 0 Е) -1
С) 2 D) 0 Е) -1
- теңсіздігін төмендегі тәсілдердің қайсысымен шығарған тиімді
А) х -дәрежеге шығарамыз да түбір деп құтыламыз
В) теңсіздіктің екі жағын да көрсеткіштік өрнектердің біреуіне бөлеміз
С) бір негізге оңай келтіріледі
D) квадтаттаймыз
Е) әрбір қосылғышты нольге теңестіреміз
- теңсіздігінің қанша бүтін шешімі бар?
А) шексіз көп В) екі С) төрт
D) сегіз Е) бүтін шешімі жоқ
- Теңсіздікті шешіңіз
А)
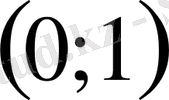 В)
В)
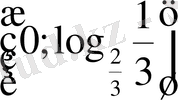 С)
С)
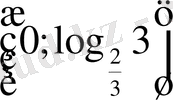
D)
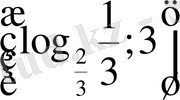 Е)
Е)
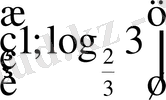
- Теңсіздікті шешіңіз
À)
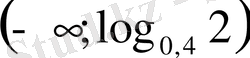 В)
В)
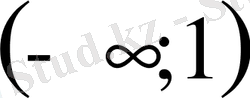 С)
С)
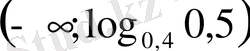
D)
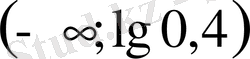 Е)
Е)
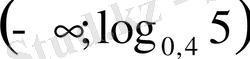
- Теңсіздікті шешіңіз
À)
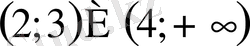 В)
В)
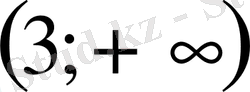 С)
С)
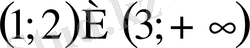
D)
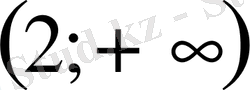 Е)
Е)
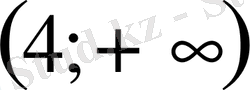
- теңсіздігін тәсілдердің қайсысымен шығарған тиімді
А) ортақ бөлгішке келтіріп, ықшамдап, көбейткішке жіктеу
В) жаңа айнымалы енгізу арқылы
С) аралықтар тәсілімен
D) теңсіздіктің оң, сол жақтарын жеке-жеке шығарып, ортақ шешімін табу
Е) графиктік тәсіл
- Теңсіздікті шешіңіз
А)
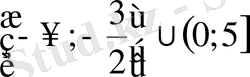 В)
В)
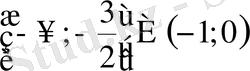
С)
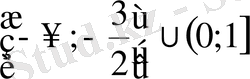 D)
D)
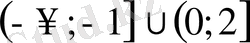
Е)
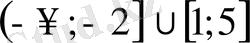
1. 3 Бақылау тапсырмалары
Теңсіздіктерді шешіңіз:
- ;
- ;
- ;
- ;
- ;
- теңсіздігінің жалғыз ғана шешімі болатынапараметрінің барлық мәндерін табыңыз.
- теңсіздігінің тек қана екі шешімі болатынапараметрінің барлық мәндерін табыңыз. Ол шешімдерді табыңыз.
- теңсіздіктер жүйесінің шешімдер жиынынүктесіне қарағанда симметриялы болатынbпараметрінің барлық мәндерін табыңыз.
- Теңсіздіктерді шешіңіз
- а- параметрінің әрбір мәні үшінтеңсіздігін қанағаттандыратынх-тің барлық мәндерін табыңыз.
1. 4 Ұлттық бірыңғай тестілеуде қолданылған тапсырмалар
Теңсіздіктерді шешіңіз:
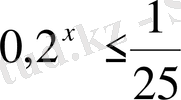
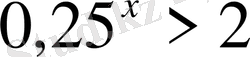
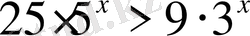
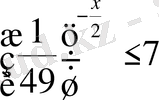
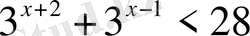
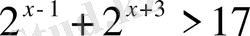
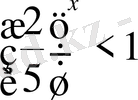
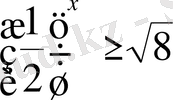
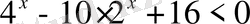
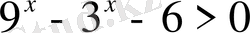
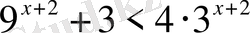
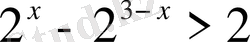
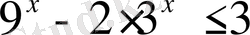
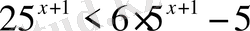
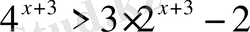
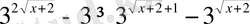
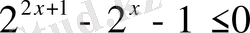
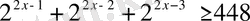
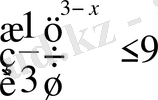
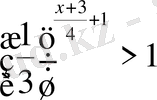
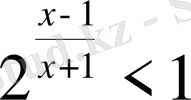
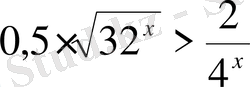
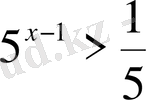
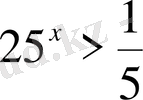
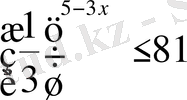
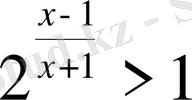
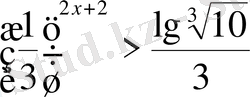
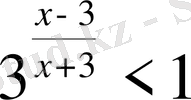
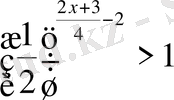
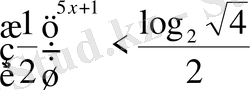
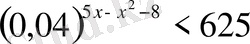
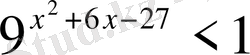

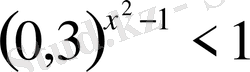
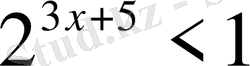
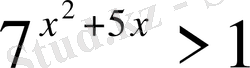
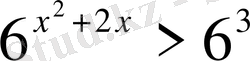
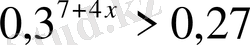
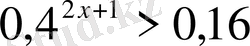
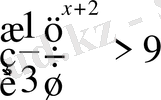
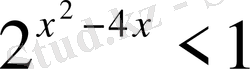
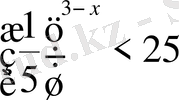
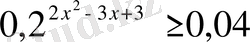
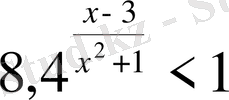
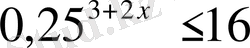 ,
х
ең үлкен бүтін шешімін тап
,
х
ең үлкен бүтін шешімін тап
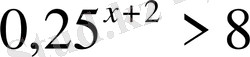 ,
х
ең үлкен бүтін шешімін тап
,
х
ең үлкен бүтін шешімін тап
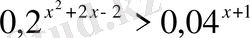
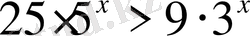
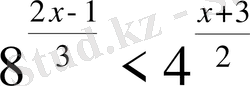
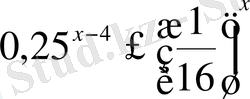
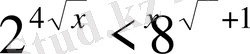
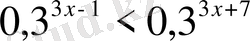
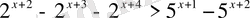
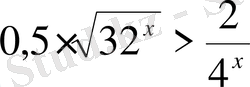
Теңсіздіктер жүйелерін шешіңіз:
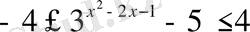
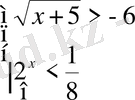
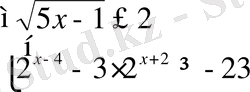
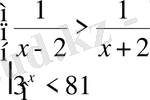
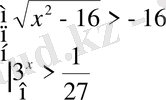
Жауабы
1. 2 Тест тапсырмалары
1. 3 Бақылау тапсырмалары
1) 2; 2) -2; 3)
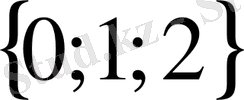 ; 4)
; 4)
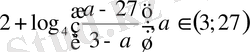 ; 5)
; 5)
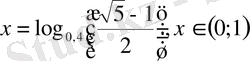 ; 6) 3; 7)
; 6) 3; 7)
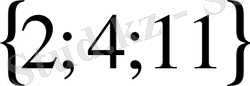 ; 8)
; 8)
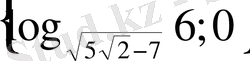 ; 9) 1, 5; 10)
; 9) 1, 5; 10)
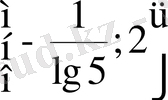 ; 11)
; 11)
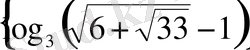 ; 12)
; 12)
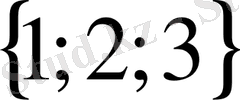 ; 13)
; 13)
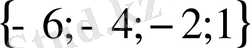 ; 14) 3; 15) 1; 16)
; 14) 3; 15) 1; 16)
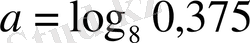 және
және
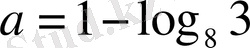 мәндерінде берілген теңдеудің бір түбірі екіншісінен 3 есе үлкен болады; 17)
мәндерінде берілген теңдеудің бір түбірі екіншісінен 3 есе үлкен болады; 17)
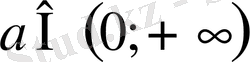 , теңдеуінің жалғыз ғана шешімі болады; 18) егер
, теңдеуінің жалғыз ғана шешімі болады; 18) егер
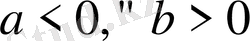 үшін немесе
үшін немесе
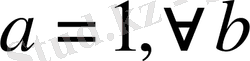 үшін теңдеудің шешімі болмайды.
үшін теңдеудің шешімі болмайды.
§ 2 Логарифмдік теңсіздіктер
Айнымалы таңба логарифм таңбасы астында немесе негізінде болып келетін теңсіздікті логарифмдік теңсіздік деп айтамыз.
Мысалы.
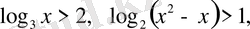
т. с. с.
Логарифмдік теңсіздіктерді шешу логарифмдік функциялардың қасиеттері мен логарифмдік теңдеулерді шешу тәсілдерімен сабақтасып жатады.
Сонымен қатар логарифмдік теңсіздіктердің шешімі көрсеткіштік теңсіздіктер секілді, логарифмнің негізіне тәуелді. Егер логаримдік өрнектің негізі бірден кіші болса, логаримді түсіріп жазғанда теңсіздік таңбасы қарама-қарсыға өзгереді, ал негізі бірден үлкен болса таңба сақталынады.
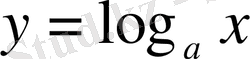 функциясының негізі бірден үлкен болса, ол - өспелі, ал бірден кіші болса - кемімелі болатындығынан:
функциясының негізі бірден үлкен болса, ол - өспелі, ал бірден кіші болса - кемімелі болатындығынан:
егер
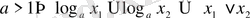 ;
;
егер
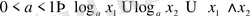 .
.
Логарифмдік теңсіздіктерге қатысты тұжырымдамалар аламыз.
Енді логаримдік теңсіздіктерді шешуді оның ең қарапайым түрлерінен бастайық:
І
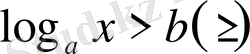 - түріндегі теңсіздік,
мұнда
- түріндегі теңсіздік,
мұнда
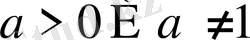 ,
b
- кез келген нақты сан.
,
b
- кез келген нақты сан.
Негізіне қатысты екі жағдайда қарастырамыз:
егер
 болса, онда
болса, онда
 ;
;
егер
 болса, онда шешім
болса, онда шешім
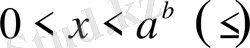 теңсіздіктері арқылы өрнектелінеді.
теңсіздіктері арқылы өрнектелінеді.
Мысалы. Теңсіздіктерді шешіңіз.
1)
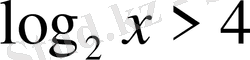 . Шығарылуы.
. Шығарылуы.
 - бірден үлкен, демек
- бірден үлкен, демек
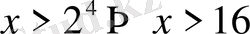 .
.
2)
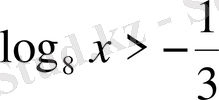 . Шығарылуы.
. Шығарылуы.
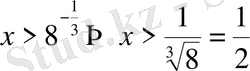 .
.
3)
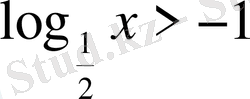 . Шығарылуы.
. Шығарылуы.
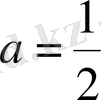 - бірден кіші, олай болса шешім
- бірден кіші, олай болса шешім
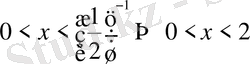 .
.
4)
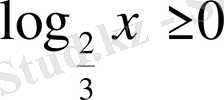 .
.
Шығарылуы.
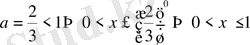 .
.
5)
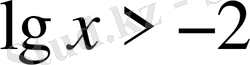 . Шығарылуы.
. Шығарылуы.
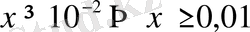 .
.
ІІ
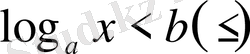 - түріндегі теңсіздік
шешімі (І) түрдегі теңсіздіктің қарама-қарсы жағдайы, яғни:
- түріндегі теңсіздік
шешімі (І) түрдегі теңсіздіктің қарама-қарсы жағдайы, яғни:
егер
 болса, онда
болса, онда
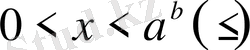 ;
;
егер
 болса, онда
болса, онда
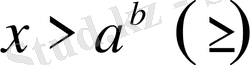 .
.
Мысалы. Теңсіздіктерді шешіңіз:
6)
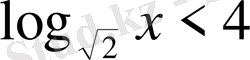 . Шығарылуы.
. Шығарылуы.
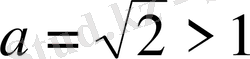 , демек
, демек
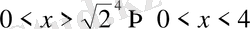 .
.
7)
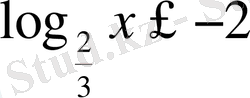 . Шығарылуы.
. Шығарылуы.
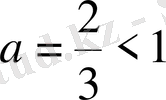 , демек таңба қарам-қарсыға өзгереді, яғни
, демек таңба қарам-қарсыға өзгереді, яғни
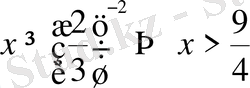 .
.
ІІІ
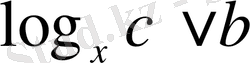 - түріндегі теңсіздік.
Мұнда
- түріндегі теңсіздік.
Мұнда
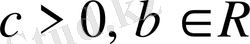 .
.
Айнымалы логаримнің негізінде болғандықтан, оның шешімі
 және
және
 жағдайларға тәуелді. Демек логаримдік теңдік, теңсіздіктер жүйесіне келтіріледі:
жағдайларға тәуелді. Демек логаримдік теңдік, теңсіздіктер жүйесіне келтіріледі:
1)
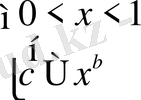 және 2)
және 2)
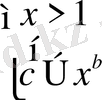
Міне осы жүйелердің шешімі бастапқы теңсіздіктің шешімі болмақ.
Ескерту.
 - теңсіздіктің төрт белгісінің бірі, ал
- теңсіздіктің төрт белгісінің бірі, ал
 - теңсіздік мағынасының қарама-қарсыға өзгергендігін көрсетеді.
- теңсіздік мағынасының қарама-қарсыға өзгергендігін көрсетеді.
Мысалы. Теңсіздіктерді шешіңіз:
8)
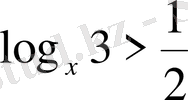 .
.
Шығарылуы. 1)
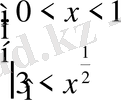 және 2)
және 2)
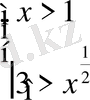 .
.
Әрбір жүйені жеке-жеке шешеміз.
1)
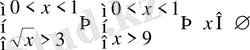 ;
;
2)
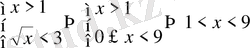 .
.
Жауап:
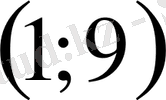 .
.
9)
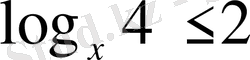 .
.
Шығарылуы. 1)
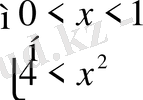 және 2)
және 2)
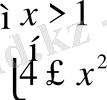 .
.
Теңсіздіктер жүйелерін шешеміз.
1)
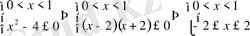 , ортақ жауап
, ортақ жауап
 ;
;
2)
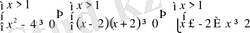 ортақ жауап
ортақ жауап
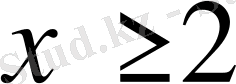 .
.
Сонда берілген теңсіздік шешімі
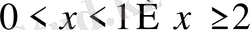
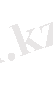 болады.
болады.
ІV
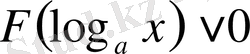 немесе
немесе
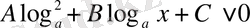 түріндегі теңсіздіктер
түріндегі теңсіздіктер
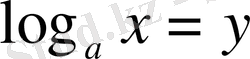 жаңа айнымалы еңгізу арқылы, қарапайым стандартты түрдегі теңсіздіктерге келтіріледі.
жаңа айнымалы еңгізу арқылы, қарапайым стандартты түрдегі теңсіздіктерге келтіріледі.
Мысалы. Теңсіздіктерді шешіңіз:
10)
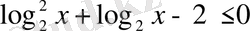 . Шығарылуы.
. Шығарылуы.
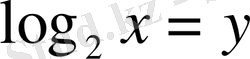 деп белгілейміз. Сонда
деп белгілейміз. Сонда
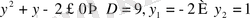 . Бұдан
. Бұдан
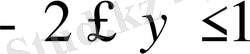 немесе
немесе
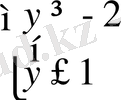 .
.
х айнымалысына қайта көшсек
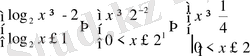 .
.
Жауап:
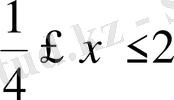 .
.
11)
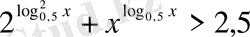 .
.
Шығарылуы.
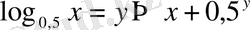 - белгілейміз. Бұдан
- белгілейміз. Бұдан
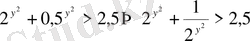 .
.
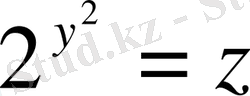 тағы белгілеу енгіземіз. Сонда
тағы белгілеу енгіземіз. Сонда
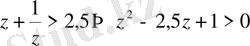 .
.
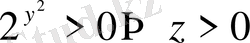 болғандықтан, квадрат теңсіздікке келтіріледі.
болғандықтан, квадрат теңсіздікке келтіріледі.
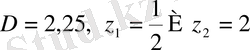 . Бұдан
. Бұдан
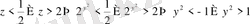 . Бірінші теңсіздіктің шешімі жоқ, екіншісінен
. Бірінші теңсіздіктің шешімі жоқ, екіншісінен
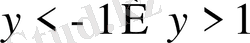 аламыз.
у
-те көмекші белгісіз, оны да
х
айнымалысына тәуелді өрнекпен қайта алмастырсақ
аламыз.
у
-те көмекші белгісіз, оны да
х
айнымалысына тәуелді өрнекпен қайта алмастырсақ
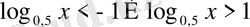 логарифмдік теңсіздіктер жиынтығын аламыз. Жауап
логарифмдік теңсіздіктер жиынтығын аламыз. Жауап
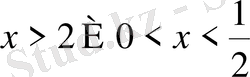 .
.
V а)
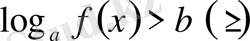 - түріндегі теңсіздік.
- түріндегі теңсіздік.
Егер
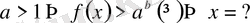 ;
;
Егер
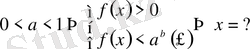 .
.
б)
- түріндегі теңсіздік.
Егер
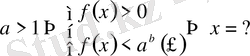 ;
;
Егер
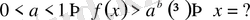 .
.
Бұл түрдегі логарифмдік теңсіздіктерді шешу барысында логарифм таңбасы ішіндегі
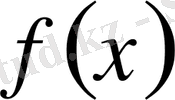 функциясының оң мәнді болуын ескерген жөн.
функциясының оң мәнді болуын ескерген жөн.
Мысалы. Теңсіздіктерді шешіңіз:
12)
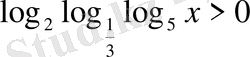 .
.
Шығарылуы.
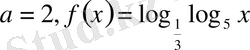 -тен түсінеміз. Бұдан
-тен түсінеміз. Бұдан
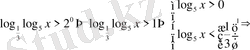
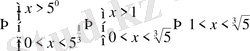 .
.
13)
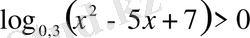 . Шығарылуы.
. Шығарылуы.
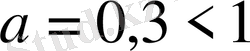 ,
,
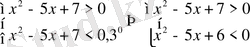 . Бірінші квадрат теңсіздік шешімі бүкіл сан осі, екіншісінікі
. Бірінші квадрат теңсіздік шешімі бүкіл сан осі, екіншісінікі
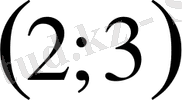 аралығы.
аралығы.
Жауап
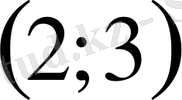
VІ
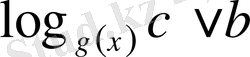 - түріндегі теңсіздік.
Мұнда
- түріндегі теңсіздік.
Мұнда
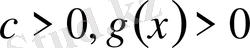 және
және
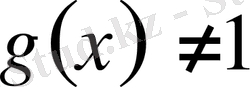 . Айнымалы шама логарифмнің негізінде болғандықтан екі түрлі жағдай қарастырылады:
. Айнымалы шама логарифмнің негізінде болғандықтан екі түрлі жағдай қарастырылады:
1)
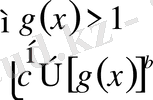 және 2)
және 2)
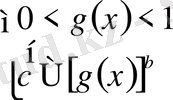 .
.
Осы теңсіздіктер жүйелерінің шешімдері бастапқы теңсіздіктің шешімі болады.
Мысалы. Теңсіздікті шешіңіз:
14)
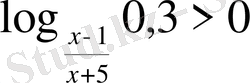 .
.
Шығарылуы. 1)
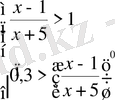 және 2)
және 2)
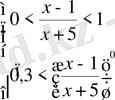 .
.
Әрбір теңсіздіктер жүйсін жеке шешеміз.
1)
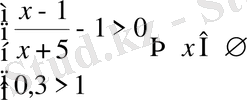 , себебі екінші теңсіздіктің мағынасы жоқ;
, себебі екінші теңсіздіктің мағынасы жоқ;
2)
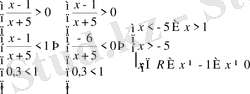 .
.
Жауап
 .
.
15)
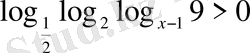 . Шығарылуы.
. Шығарылуы.
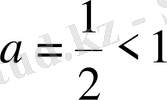 және
және
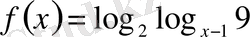 .
.
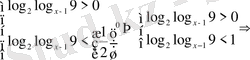
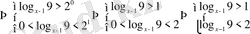 қарастырылып отырған түрдегі теңсіздіктер жүйесіне келтірдік. Бұдан 1)
қарастырылып отырған түрдегі теңсіздіктер жүйесіне келтірдік. Бұдан 1)
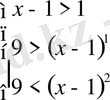 және 2)
және 2)
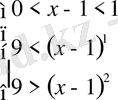 .
.
Әрбір жүйені жеке шешеміз.
1)
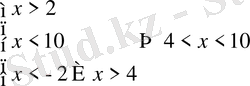 ;
;
2)
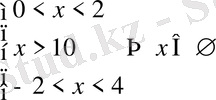 .
.
Жауап
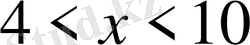 .
.
VІІ
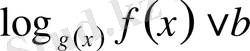 - түріндегі теңсіздік.
Мұнда
- түріндегі теңсіздік.
Мұнда
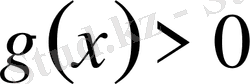 және
және
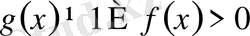 . Бұл тұрғыдағы теңсіздіктердің шешімі де теңсіздіктер жүйесіне келтіру арқылы шешіледі:
. Бұл тұрғыдағы теңсіздіктердің шешімі де теңсіздіктер жүйесіне келтіру арқылы шешіледі:
1)
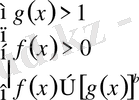 және 2)
және 2)
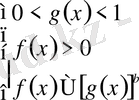 .
.
Осы теңсіздіктер жүйелерінің шешімдері бастапқы теңсіздіктің шешімі болады.
Мысалы. Теңсіздікті шешіңіз:
16)
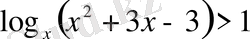 . Шығарылуы.
. Шығарылуы.
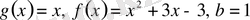 . Ережеге сүйенсек:
. Ережеге сүйенсек:
1)
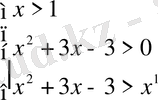 және 2)
және 2)
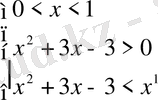 .
.
Енді бұл теңсіздіктер жүйелерінің логарифмдерге қатысы жоқ. Әрқайсысын жеке шешеміз.
1)
 . Бұл жүйенің шешімі
. Бұл жүйенің шешімі
 ;
;
2)
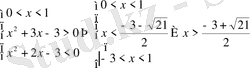 .
.
Еікінші теңсіздіктер жүйесінің шешімі
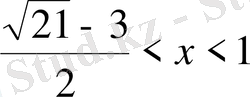
Жауап
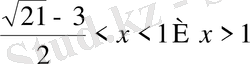 .
.
VІІІ
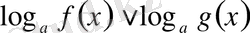 - түріндегі теңсіздік.
- түріндегі теңсіздік.
Егер
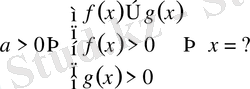
Егер
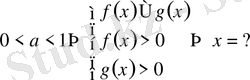
Мысалы. Теңсіздікті шешіңіз:
17)
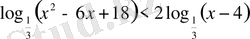 .
.
Шығарылуы.
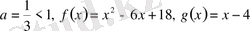 . Логарифмнің мағынасы болуы үшін бұл функциялар оң болуы қажет. Демек
. Логарифмнің мағынасы болуы үшін бұл функциялар оң болуы қажет. Демек
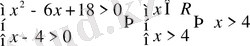 . Негізі бірден кіші болғандықтан теңсіздіктің мағынасы, негіздерін түсіргенде қарама қарсы өзгереді
. Негізі бірден кіші болғандықтан теңсіздіктің мағынасы, негіздерін түсіргенде қарама қарсы өзгереді
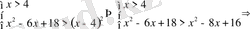
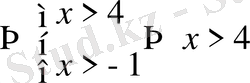 .
.
18)
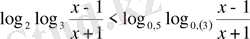 .
.
Шығарылуы. Сыртқы логарифмдердің негіздерін бірдей түрге келтіреміз
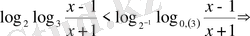
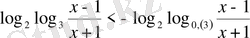
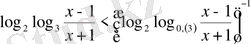
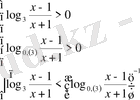
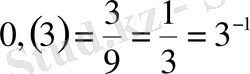 , яғни негіздерін бірдей түрге келтіреміз. Үшінші теңсіздікті жеке қарастырайық
, яғни негіздерін бірдей түрге келтіреміз. Үшінші теңсіздікті жеке қарастырайық
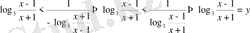 деп белгілесек
деп белгілесек
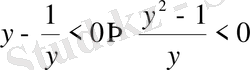
у
айнымалысын қайта алмастырсақ
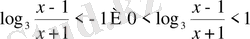 теңсіздіктер жүйесін аламыз. Тапсырманы аяқтау оқырманға міндеттелінеді. Жауап
теңсіздіктер жүйесін аламыз. Тапсырманы аяқтау оқырманға міндеттелінеді. Жауап
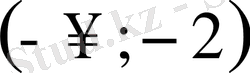 .
.
Ескерту.
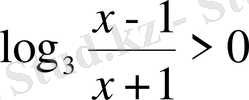 екендігін ескеріп бірінші теңсіздікті қарастырмаса да болады.
екендігін ескеріп бірінші теңсіздікті қарастырмаса да болады.
ІХ
 - түріндегі теңсіздік.
Мұнда
- түріндегі теңсіздік.
Мұнда
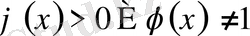 және
және
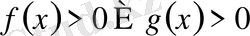 кез келген функциялар.
кез келген функциялар.
1)
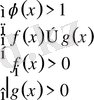 және 2)
және 2)
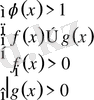 .
.
Осы теңсіздіктер жүйелерінің шешімі берілген теңсіздіктің шешімі болады.
Мысалы. Теңсіздікті шешіңіз:
19)
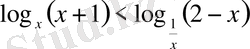 .
.
Шығарылуы.
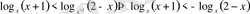
.
Бұл теңсіздікті шешпес бұрын, берілген теңсіздіктің анықтау облысын (мүмкін мәндер облысын) табайық, ол теңсіздікті шешу жолын жеңілдетеді
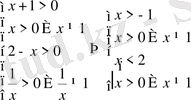 .
.
Демек теңсіздік шешімі
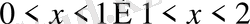 аралығында ғана жатуы керек. Сонымен
аралығында ғана жатуы керек. Сонымен
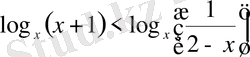
1)
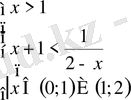 және 2)
және 2)
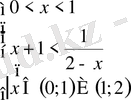 .
.
Тапсырманы аяқтау оқырманға міндеттелінеді.
Жауап
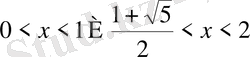 .
.
20) Қайсыбір жағдайларда теңсіздіктерді жалпыға ортақ тәсілдермен шығару мүмкін бола бермейді. Есеп шартына байланысты ой қорытылып, жауабы анықталынады.
Мысал. Теңсіздікті шешіңіз:
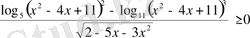 .
.
Шығарылуы. Бөлшек оң мән қабылдайды. Егер оның алымындағы және бөліміндегі өрнектердің таңбалары бірдей болса, ал берілген өрнектің бөлімі
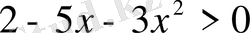 болса, әрқашанда оң мәнді болады. Демек теңсіздіктің анықталу облысы
болса, әрқашанда оң мәнді болады. Демек теңсіздіктің анықталу облысы
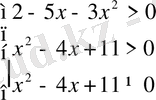 теңсіздіктер жүйесінің ортақ шешімі
теңсіздіктер жүйесінің ортақ шешімі
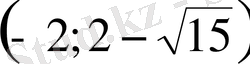 болады.
болады.
Бұдан қарастырып отырған облыста
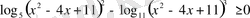 шешімін тапсақ жеткілікті. Бірақ бұл теңсіздікті бір негізге келтіріп, ережеге сәйкес шығару көп уақытты, ұзақ есептеулерді қажет етеді. Сондықтан қосындыдағы әрбір өрнектің теңсіздіктің анықталу облысындағы таңбаларын анықтайық, яғни
шешімін тапсақ жеткілікті. Бірақ бұл теңсіздікті бір негізге келтіріп, ережеге сәйкес шығару көп уақытты, ұзақ есептеулерді қажет етеді. Сондықтан қосындыдағы әрбір өрнектің теңсіздіктің анықталу облысындағы таңбаларын анықтайық, яғни
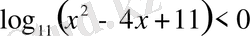 теңсіздігінің шешімі қандай аралықта жататынын қарастырайық.
теңсіздігінің шешімі қандай аралықта жататынын қарастырайық.
Онда
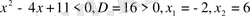 . Демек
. Демек
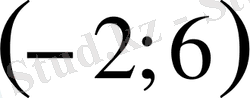 аралығында қарастырып отырған өрнек теріс мән қабылдайды. Ал
аралығында қарастырып отырған өрнек теріс мән қабылдайды. Ал
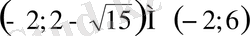 жиыншасы болып келеді. Яғни
жиыншасы болып келеді. Яғни
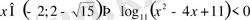 . Енді
. Енді
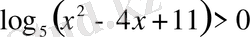 болатынын көрсетсек, жеткілікті
болатынын көрсетсек, жеткілікті
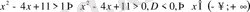 , бұдан
, бұдан
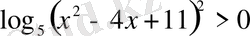 , кез келген
х
үшін, оң мәнді.
, кез келген
х
үшін, оң мәнді.
Бұдан бастапқы теңсіздіктің шешімі
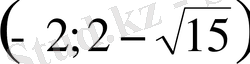 аралығы деген қорытындыға келеміз.
аралығы деген қорытындыға келеміз.
Аралас типтегі өрнектерден тұратын теңсіздіктерді шешу барысында аралықтар (интервалдар) тәсілін қалданған да тиімді.
Ол үшін берілген өрнектің анықталу облысында берілген өрнектің алымы мен бөлімінің таңбаларын анықтап қажетті аралықты, іріктеп аламыз.
Мысал. Теңсіздікті шешіңіз:
21)
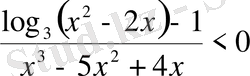 .
.
Шығарылуы. Теңсіздіктің анықталу облысы
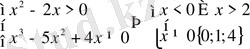 ,
,
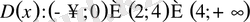 .
.
Міне осы облыста өрнектің таңбасын анықтайық. Ол үшін бөлшектің алымы мен бөлімінің ноль нүктелері арқылы әрбір аралықтағы таңбаларын зерттейміз.
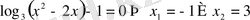

Бізге қажетті бөлшектің теріс болатын мәндері, демек бөлшектің алымы мен бөліміндегі өрнектердің таңбалары әртүрлі болуы керек.
Жауап
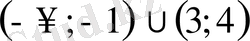 .
.
2. 1. Қайталауға арналған сұрақтар
- Ең қарапайым логаримдік теңсіздіктердің шешімі қалай жазылады?
- Белгісіз шама логаримдік өрнектің негізінде болған жағдайда теңсіздік қалай шешіледі?
- Логаримдік теңсіздіктерге қандай жағдайларда жаңа айнымалы енгіземіз.
- болған жағдайда, теңсіздік шешімін қалай табамыз?
- Логарифмдік теңсіздіктерді шешуге аралықтар тәсілін қолдануға бола ма? Болатын болса, негізгі қағида не болып есептелінеді?
2. 2 Тестік тапсырмалар
1. Төмендегі сандарды қайсысы теңсіздікті қанағаттандырады
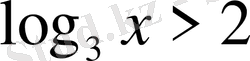
А) 3 В) 9 С) 10 D) 1 Е)

2. Төмендегі сандардың қайсысы теңсіздіктің шешімі бола алады?
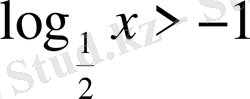
А) 0 В)
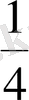 С) 4 D) 3 Е) -2
С) 4 D) 3 Е) -2
3. Сандық өрнектерің ең үлкенін көрсетіңіз
А)
 В)
В)
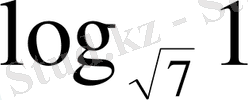 С)
С)
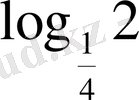 D)
D)
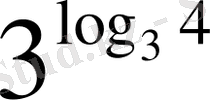 Е)
Е)
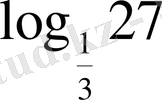
4. Теңсіздікті шешіңіз
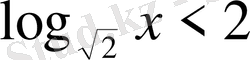
А)
 В)
В)
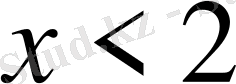 С)
С)
 D)
D)
 Е)
Е)

5. Теңсіздікті шешіңіз
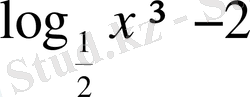
А)
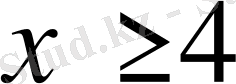 В)
В)
 С)
С)
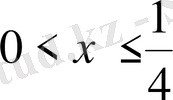 D)
D)
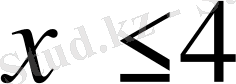 Е)
Е)

6. Теңсіздікті шешіңіз
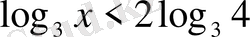
А)
 В)
В)
 С)
С)
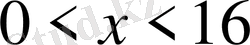
D)
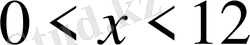 Е)
Е)

7. Теңсіздікті шешіңіз
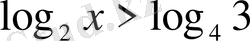
А)
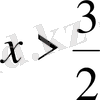 В)
В)
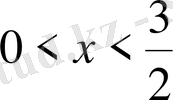 С)
С)
 D)
D)
 Е)
Е)

8. Теңсіздікті шешіңіз x>9
А)
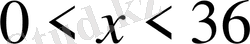 В)
В)
 С)
С)

D)
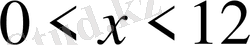 Е)
Е)
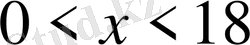
9. Теңсіздікті шешіңіз
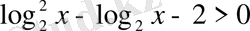
А)
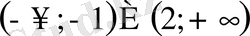 В)
В)
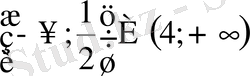
С)
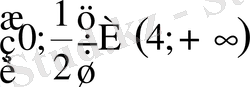 D)
D)
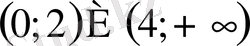 Е)
Е)
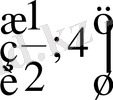
10. Теңсіздікті шешіңіз
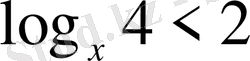
А)
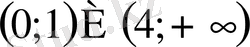 В)
В)
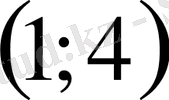 С)
С)
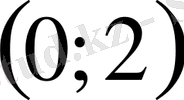
D)
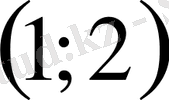 Е)
Е)
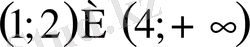
11. Теңсіздікті шешіңіз
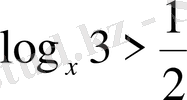
А)
 В)
В)
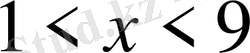 С)
С)
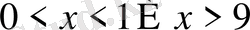
D)
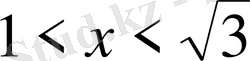 Е)
Е)
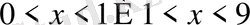
12. Теңсіздікті шешіңіз
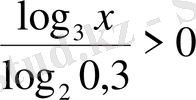
А)
 В)
В)
 С)
С)
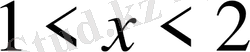 D)
D)
 Е)
Е)

13. Теңсіздікті шешіңіз
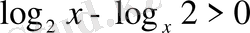
А)
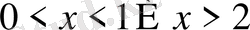 В)
В)
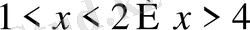
С)
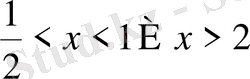 D)
D)
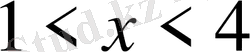 Е)
Е)

14. Теңсіздікті шешіңіз
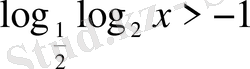
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz