Көрсеткіштік және логарифмдік теңдеулер: түрлері, шешу тәсілдері және тапсырмалар


ІІ Бөлім. Трансцендентті теңдеулер
§1 Көрсеткіштік теңдеулер
Трансцендентті теңдеулер деп айнымалы трансцендентті функциялар арқылы өрнектелінген немесе алгебралық емес теңдеулерді айтамыз. Бұндай теңдеулерге көрсеткіштік, логарифмдік, тригонометриялық және кері тригонометриялық теңдеулер жатады.
Біз бұл бөлімде трансцендентті теңдеулерді шешудің негізгі тәсілдерін қарастырамыз.
Айнымалы алгебралық өрнектің немесе тұрақты бір шаманың дәреже көрсеткішінде болып келетін теңдеулерді - көрсеткіштік теңдеулер деп атаймыз.
Көрсеткіштік теңдеулерді шешу негізінен дәреженің қасиеттеріне сүйенеді. Негіздері бірдей және оң, бірден өзгеше екі көрсеткіштік функция өзара тең болады, сонда тек сонда ғана егер олардың дәреже көрсеткіштері өзара тең болса, яғни
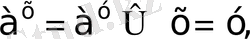

Сонымен қатар көрсеткіштік теңдеулерді шешуде көрсеткіштік функцияның қасиеттері де жиі қолданылады.
Көрсеткішті теңдеулерді шешудің жалпыға ортақ ережесі жоқ, бірақ элементар математиканың әдіс-тәсілдерімен шығарылатын теңдеулер топтамасын жиі кездестіруге болады.
Енді көрсеткіштік теңдеулердің негізгі түрлерін шешу тәсілдерін қарастырайық
І
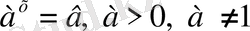 түріндегі теңдеу. Мұнда
түріндегі теңдеу. Мұнда
 кез келген бір тұрақты шама, бірақ теңдеу шешімі осы тұрақтының мәніне тәуелді.
кез келген бір тұрақты шама, бірақ теңдеу шешімі осы тұрақтының мәніне тәуелді.
1) Егер
 теріс сан
теріс сан
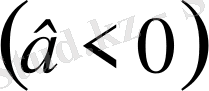 немесе нольге тең болса
немесе нольге тең болса
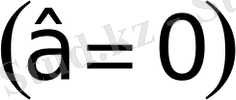 , онда теңдеудің шешімі болмайды.
, онда теңдеудің шешімі болмайды.
2) Егер
 оң сан болса
оң сан болса
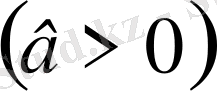 болса, теңдеудің жалғыз ғана шешімі болады.
болса, теңдеудің жалғыз ғана шешімі болады.
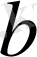 -ның қабылдайтын мәндерінің дербес жағдайын қарастырайық.
-ның қабылдайтын мәндерінің дербес жағдайын қарастырайық.
а)
 =1 болсын, онда
=1 болсын, онда
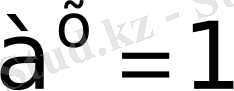 түріндегі теңдеудің шешімі
түріндегі теңдеудің шешімі
 болады;
болады;
б)
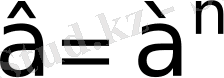 яғни
яғни
 саны
саны
 негіздегі бір санға тең болсын, онда
негіздегі бір санға тең болсын, онда
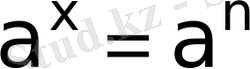 теңдеуінің шешімі
теңдеуінің шешімі
 болады;
болады;
в)
 саны бірден өзгеше және негізі
саны бірден өзгеше және негізі
 арқылы өрнектелетін санға келтірілмесін, онда
арқылы өрнектелетін санға келтірілмесін, онда
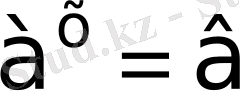 теңдеуінің шешімі
теңдеуінің шешімі
 саны болады.
саны болады.
Мысалы . Теңдеулерді шешіңіз
1)
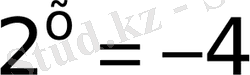
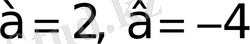 бірақ
бірақ
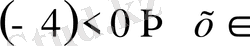 Ш
Ш
2)
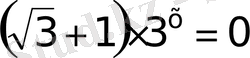
Бірінші көбейткіш
 айнымалысына тәуелсіз, әрі нольден өзгеше шама бұдан
айнымалысына тәуелсіз, әрі нольден өзгеше шама бұдан
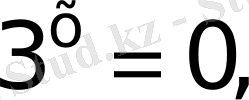 бірақ көрсеткіштік функция әрқашанда оң мәнді қабылдайды
бірақ көрсеткіштік функция әрқашанда оң мәнді қабылдайды
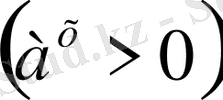 демек ол айнымалының кез келген мәнде нольге тең бола алмайды
демек ол айнымалының кез келген мәнде нольге тең бола алмайды
 Ш
Ш
3)
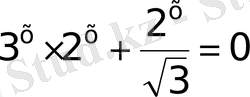
 - ортақ көбейткіш, жақша сыртына шығарсақ, теңдеу көбейткіштерге жіктелінеді
- ортақ көбейткіш, жақша сыртына шығарсақ, теңдеу көбейткіштерге жіктелінеді
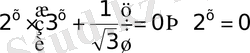

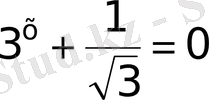
а)
 Ш
Ш
б)
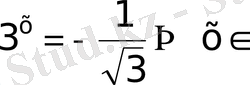 Ш
Ш
Бұдан теңдеудің шешімі жоқ деген қорытындыға келеміз.
4)
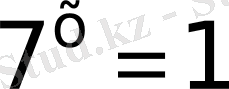
Дәреженің қасиетіне сүйенсек
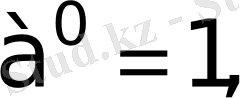 бұдан
бұдан
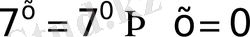
5)
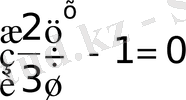
Айнымалысы бар өрнекті теңдіктің бір жағына қалдырып қалғанын қарама қарсы таңбамен екінші жағын өткіземіз
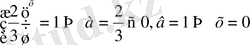
6)
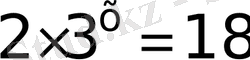
Теңдіктің екі жағын да 2-ге бөлеміз
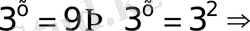 негіздері бірдей, дәреже көрсеткіштерін теңестіреміз
негіздері бірдей, дәреже көрсеткіштерін теңестіреміз

7)
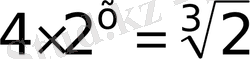
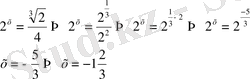
8)
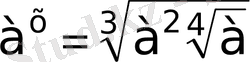
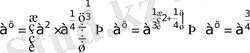

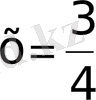
9)
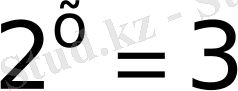
2 мен 3 ешқашанда бірдей, ортақ негізге келмейді, демек
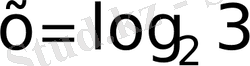
10)

10 саны 5-ке тәуелді болғанымен негізі 5 болатын сан арқылы өрнектелінбейді демек

ІІ
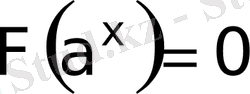 түріндегі теңдеу
түріндегі теңдеу
Дербес жағдайда
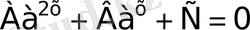
түріндегі теңдеулер, жиі кездеседі.
Мұнда А, В, С -
const
және
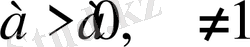
Бұл түрдегі теңдеулер
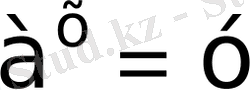 алмастыруы арқылы,
алмастыруы арқылы,
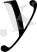 айнымалысына тәуелді қарапайым теңдеуге келтіріледі.
айнымалысына тәуелді қарапайым теңдеуге келтіріледі.
Көмекші белгісіздің табылған мәндерін орнына қойсақ, бастапқы теңдеуге эквивалентті теңдеулер аламыз.
Мысалы. Теңдеулерді шешіңіз
11)
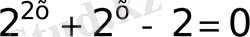
Бұл теңдеуде негіздері бірдей екен деп, оларды түсіріп жазуға болмайды
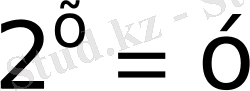 деп белгілесек
деп белгілесек
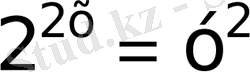 болады.
болады.
Бұдан
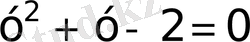 квадрат теңдеу аламыз
квадрат теңдеу аламыз


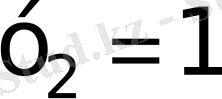 Орнына қайта қойсақ
Орнына қайта қойсақ
а)
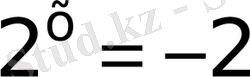 және б)
және б)
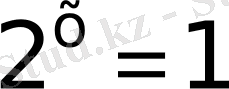
яғни берілген теңдеу екі қарапайым теңдеуге жіктелінді.
Біріншісінің шешімі жоқ, екіншісінен
 . Жауап
. Жауап

12)
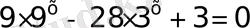
Айнымалыға тәуелді өрнектердің негіздері әртүрлі, бірақ олар бірдей негізге келтірілетінін оңай байқауға болады, яғни
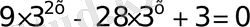 теңдеуін аламыз
теңдеуін аламыз
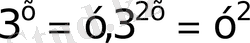 десек
десек
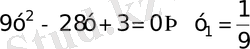

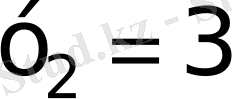
а)
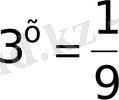 және б)
және б)
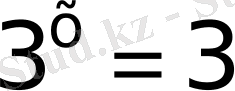 . Жауап
. Жауап
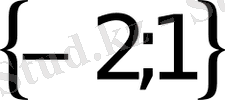
13)
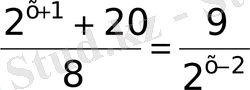
 -і бар өрнектердің негіздері бірдей болғанмен, дәреже көрсеткіштері әр түрлі яғни түрлендіріп, мүмкін болса бірдей түрге келтіреміз
-і бар өрнектердің негіздері бірдей болғанмен, дәреже көрсеткіштері әр түрлі яғни түрлендіріп, мүмкін болса бірдей түрге келтіреміз
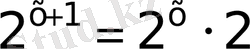

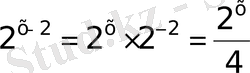
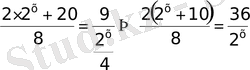
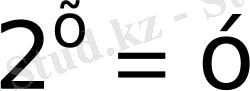 деп белгілеп, теңдіктің сол жағын 2-ге қысқартсақ
деп белгілеп, теңдіктің сол жағын 2-ге қысқартсақ
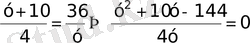
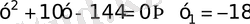

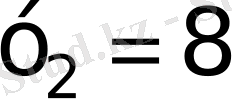
а)
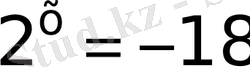
 б)
б)
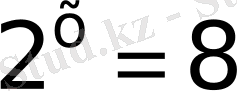 жауап
жауап

ІІІ Біртекті көрсеткіштік теңдеулерді шешу
1)
 түріндегі теңдеу мұнда
түріндегі теңдеу мұнда
 - оң және бірден өзгеше сандар,
- оң және бірден өзгеше сандар,
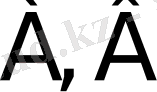 -
const.
-
const.
Егер
 мен
мен
 сандары бірдей негізге келтірілмейтін болса, теңдіктің екі жағын да не
сандары бірдей негізге келтірілмейтін болса, теңдіктің екі жағын да не
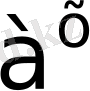 , немесе
, немесе
 бөлеміз. Нәтижесінде
бөлеміз. Нәтижесінде
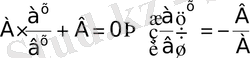
түріне келтіріледі.
Мысалдар Теңдеуді шешіңіз
14)
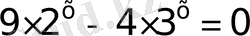
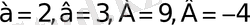 -ке тең 2 мен 3 сандарын бірдей негізге келтіру мүмкін емес, бірақ теңдеу біртекті.
-ке тең 2 мен 3 сандарын бірдей негізге келтіру мүмкін емес, бірақ теңдеу біртекті.
Барлық қосылғыштың дәреже корсеткіштері өзара тең. Демек теңдіктің екі жағын да
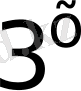 бөлеміз
бөлеміз
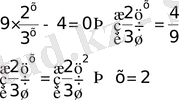
15)
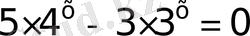
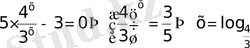
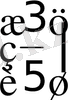
16)
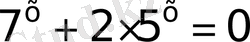
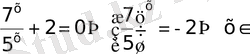 Ш
Ш
17)
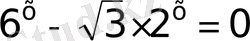
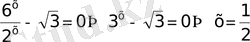
2)
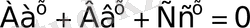 түріндегі теңдеу де біртекті теңдеу болып есептелінеді.
түріндегі теңдеу де біртекті теңдеу болып есептелінеді.
Мұнда да негіздері оң, әрі бірден өзгеше сандар
 -
const
.
-
const
.
Бұндай теңдеулер үшін көпшілік жағдайда
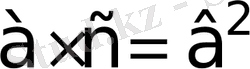 теңдігі орындалады. Теңдіктің екі жағын да
теңдігі орындалады. Теңдіктің екі жағын да
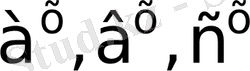 өрнектерінің біреуіне бөлеміз. Сонда
өрнектерінің біреуіне бөлеміз. Сонда
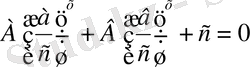 теңдеуіне келеді. Одан кейін көмекші белгісіз еңгізу арқылы квадрат теңдеу аламыз.
теңдеуіне келеді. Одан кейін көмекші белгісіз еңгізу арқылы квадрат теңдеу аламыз.
Мысалы Теңдеулерді шешіңіз
18)
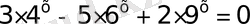
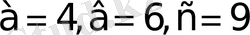 және
және
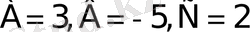 -ге тең,
-ге тең,
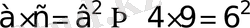 Теңдеу біртекті, демек теңдіктің екі жағын да
Теңдеу біртекті, демек теңдіктің екі жағын да
 бөлеміз.
бөлеміз.
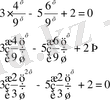
Есепті аяқтау оқырманға жүктелінеді. Жауап

19)
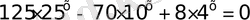
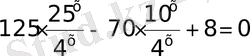
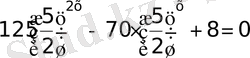
Есепті аяқтау оқырманға жүктеледі. Жауап
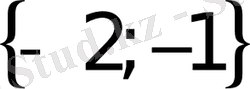
ІV
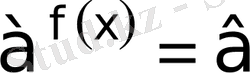 Equation. 3 түріндегі теңдеу.
Equation. 3 түріндегі теңдеу.
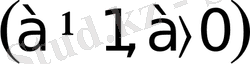 Equation. 3 Мұнда
Equation. 3 Мұнда
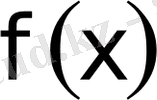 Equation. 3 кез келген рационал функция
Equation. 3 кез келген рационал функция
 Equation. 3 -нақты сан.
Equation. 3 -нақты сан.
1) егер
 Equation. 3 теріс сан немесе нольге тең болса, онда теңдеудің шешімі болмайды;
Equation. 3 теріс сан немесе нольге тең болса, онда теңдеудің шешімі болмайды;
2) егер
 Equation. 3 оң сан болса, онда оның шешімін табу үшін бірнеше дербес жағдайда қарастырамыз
Equation. 3 оң сан болса, онда оның шешімін табу үшін бірнеше дербес жағдайда қарастырамыз
а)
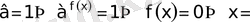 Equation. 3 ?
Equation. 3 ?
б)
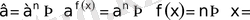 Equation. 3 ?
Equation. 3 ?
в) кез келген
 Equation. 3 үшін
Equation. 3 үшін
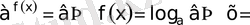 Equation. 3 ?
Equation. 3 ?
Мысалдар. Теңдеулерді шешіңіз
20)
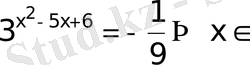 Ш
Ш
- Ш
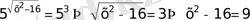
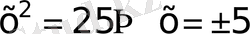
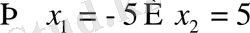
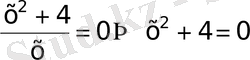 ∪
∪

 Ш
Ш
Теңдіктің сол жағындағы өрнекті бір негізге келтіріп, дәрежесінің қасиетіне сүйеніп ықшамдаймыз
а)
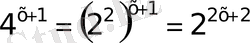
б)
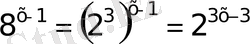
в)
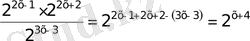
г)
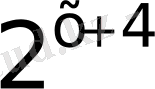
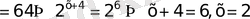
25)
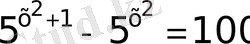
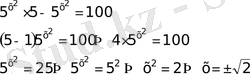
26)
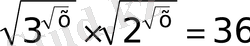
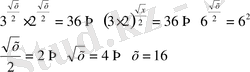
27)
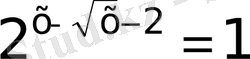
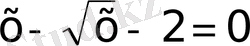
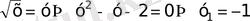

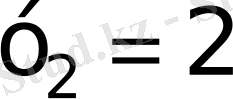
а)
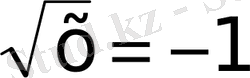
 б)
б)
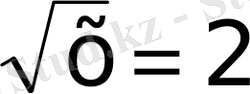 жауап
жауап

28)
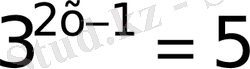
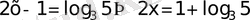
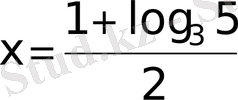
29)
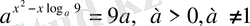
Бір қарағанда, негіздерінің арасында ұқсастық болғанымен, бірдей емес демек дәреже көрсеткіштеріндегі айнымалыны логарифм арқылы өрнектейміз
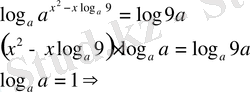
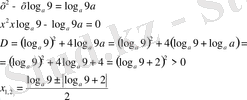
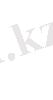 жауаптың
жауаптың
 параметрінің мәндеріне тәуелділігін көрсету оқырманға жүктелінеді.
параметрінің мәндеріне тәуелділігін көрсету оқырманға жүктелінеді.
30)
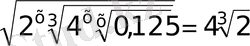
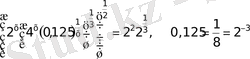
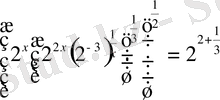

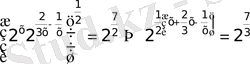
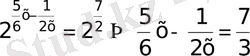
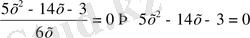
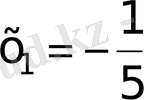

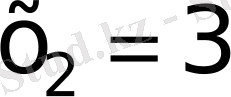
V
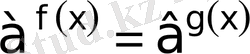 . 3 түріндегі теңдеуді
. 3 түріндегі теңдеуді
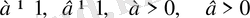 . 3
. 3
Мұнда
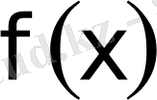 . 3 және
. 3 және
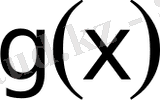 . 3 кез келген рационал функциялар.
. 3 кез келген рационал функциялар.
Бұл түрдегі теңдеулерді көпшілік жағдайда негіздері бірдей түрге келтіріледі
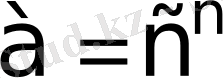 және
және
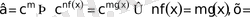 ?
?
Мысалдар. Теңдеулерді шешіңіз
31)
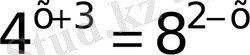
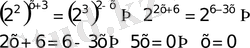
32)
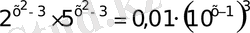
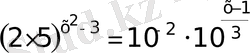
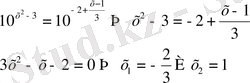
Егер теңдеудегі көрсеткіштік өрнектер бір негізге келтірілмейтін болса теңдіктің екі жағында кез келген бір
 негізінде логарифмдейміз
негізінде логарифмдейміз
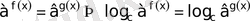
Бұдан логарифмнің қасиетіне сүйеніп, дәреже көрсеткіштерін түсіріп жазамыз
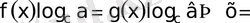 ?
?
Мысалы. Теңдеуді шешіңіз
33)
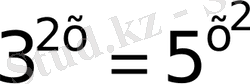
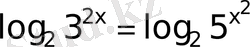
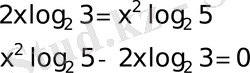
Толымсыз квадрат теңдеу
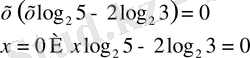
а)
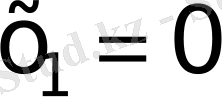
б)
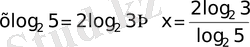
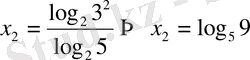
VІ
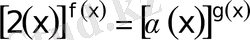 . 3 түріндегі теңдеу.
. 3 түріндегі теңдеу.
Мұнда
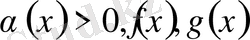 . 3 кез келген рационал функциялар.
. 3 кез келген рационал функциялар.
Теңдеудің бұндай түрлерін теңдіктің екі жағын да бірдей негізге логарифмдеу арқылы шығарамыз нәтижесінде
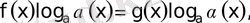 . 3 демек теңдеу
. 3 демек теңдеу
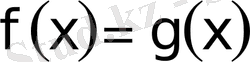 . 3 және
. 3 және
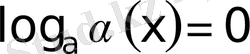 . 3 теңдеулер жиынтығына эквивалентті болады.
. 3 теңдеулер жиынтығына эквивалентті болады.
Мысалдар. Теңдеулерді шешіңіз
34)
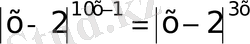
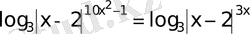
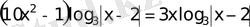
а)
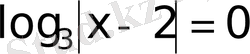 және б)
және б)
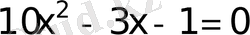
Бірінші теңдеудің түбірлері

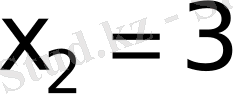 екінші теңдеудің түбірлері
екінші теңдеудің түбірлері
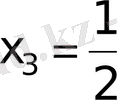 ,
,
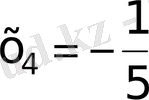 Жауап
Жауап
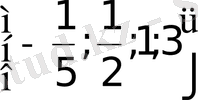
35)
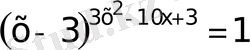
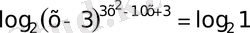
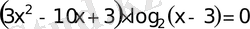
а)
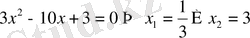
Бірақ
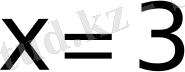 бөтен түбір себебі теңдеудің анықталу облысы
бөтен түбір себебі теңдеудің анықталу облысы
 немесе оған тексеру нәтижесінде де көз жеткізуге болады
немесе оған тексеру нәтижесінде де көз жеткізуге болады
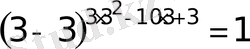
0
0
=1
 0
0
- анықталмайды;
0
0
- анықталмайды;
б)
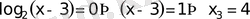 жауап
жауап
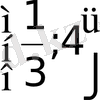
Логарифмдік теңдеулердің негізгі түрлерін келесі параграфтарға қарастырамыз, бірақ көрсеткіштік функция мен логарифмдік функциялар өзара кері функциялар болғандықтан, көптеген теңдеулер шешу барысында, олар бір-бірін толықтырып отырады. Сондықтан логарифмдік өрнектердің қатысынсыз тақырыпты толық ашып көрсету мүмкін емес.
Қайсыбір түсініксіз тужырымдамалар мен өрнектер кездессе, келесі параграфтағы тапсырмаларды талдаудан кейін қайта оралып, талдаған тиімдірек болар еді.
36)
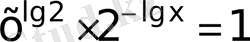
Теңдеудің анықталу облысы
 .
.
Теңдеуді оң негізінде логарифмдейміз
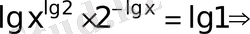
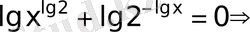

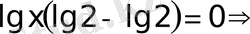
 жауап
жауап
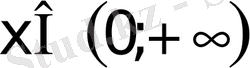
VІІ
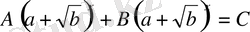 түріндегі теңдеу,
түріндегі теңдеу,
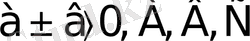 -
соnst
. Бұл түрдегі теңдеулер үшін
-
соnst
. Бұл түрдегі теңдеулер үшін
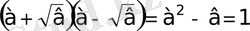 (*)
(*)
теңдігі орындалады, яғни
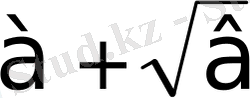 және
және
 сандары өзара кері сандар. Сондықтан
сандары өзара кері сандар. Сондықтан
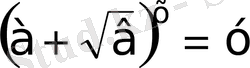 деп белгілесек
деп белгілесек
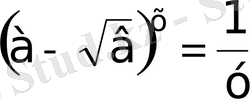 болады, демек теңдеу
болады, демек теңдеу
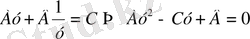 квадрат теңдеуге келтіріледі.
квадрат теңдеуге келтіріледі.
Мысал. Теңдеуді шешіңіз
37)
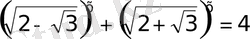
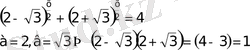
яғни олар өзара кері сандар
 . 3 деп белгілесек
. 3 деп белгілесек
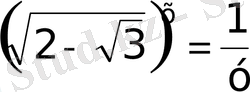 . 3
. 3
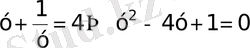

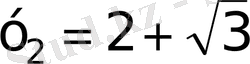
а)
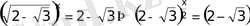
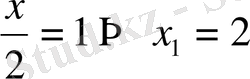
б)
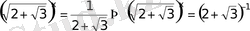
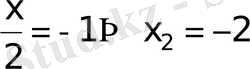 жауап
жауап
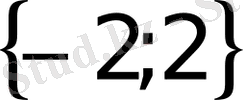
VІІІ
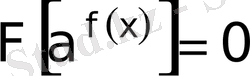 . 3 түріндегі теңдеу
. 3 түріндегі теңдеу
Егер берілген теңдеу айнымалы бір ғана көрсеткіштің өрнек арқылы берілсе,
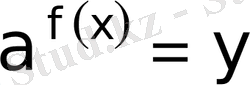 . 3 де көмекші белгісіз белгілеп теңдеуді ықшамдап шешіп бастапқы айнымалыға қайта көшеміз. Нәтижесінде бастапқы теңдеуге пара-пар теңдеулер жиынтығын аламыз.
. 3 де көмекші белгісіз белгілеп теңдеуді ықшамдап шешіп бастапқы айнымалыға қайта көшеміз. Нәтижесінде бастапқы теңдеуге пара-пар теңдеулер жиынтығын аламыз.
Мысалдар. Теңдеулерді шешіңіз
38)
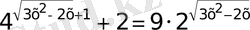 . 3
. 3
Біз басты назарды, көрсеткіштік өрнектерге аударамыз
а) олардың негіздерін бірдей түрге келтіреміз;
б) дәреже көрсеткіштерін бірдей түрге келтіреміз;
в) көмекші белгісіз еңгіземіз
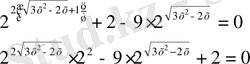
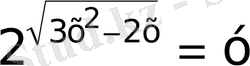 деп белгілесек
деп белгілесек
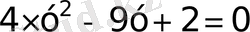 квадрат теңдеуін аламыз
квадрат теңдеуін аламыз
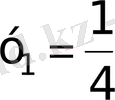 және
және
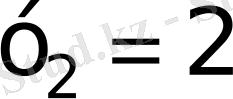
а)
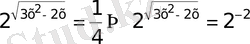 . 3
. 3
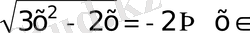 . 3Ш (шешімі жоқ)
. 3Ш (шешімі жоқ)
б)
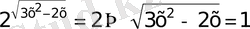 . 3
. 3
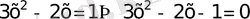
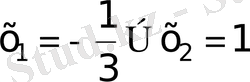 жауап
жауап
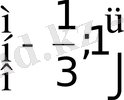
39)
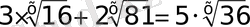
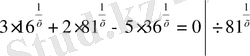
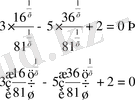
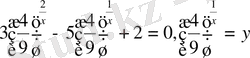 Equation. 3 деп белгілесек
Equation. 3 деп белгілесек
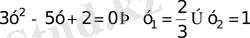 . 3, бұдан
. 3, бұдан
а)
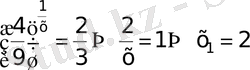 . 3
. 3
б)
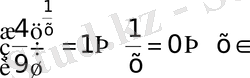 . 3Ш. Жауап
. 3Ш. Жауап
 . 3
. 3
Көрсеткіштік теңдеулердің қайсыбір түрін шешкенде, тек сол теңдеудің өзіне тән ерекшеліктерін ескере отырып, қажетті түрлендірулер жасаймыз.
Мысал. Теңдеуді шешіңіз
40)
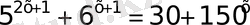 . 3
. 3
Теңдеудегі көрсеткіштік өрнектердің негіздері әртүрлі, сонымен қатар 5 пен 6 бір негізге ешқашанда келмейді және теңдеу біртектіде емес

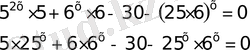
Берілген теңдеудегі үш түрлі негізден екі түрлі негізге көшірдік.
Енді қосылғыштарды топтастырып көбейткішке жіктейік
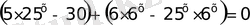
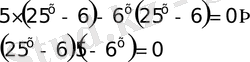
а)
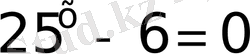
 б)
б)
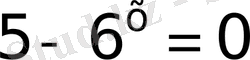
жауап

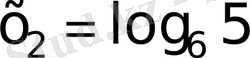
41)
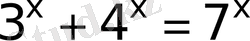
Біртекті теңдеу, бірақ қосылғыштарды бір негізге келтіру мүмкін емес, тек айнымалыға бірнеше мән беріп, тексеру нәтижесінде ғана теңдеудің шешімінің
 екендігінде көз жеткізуге болады.
екендігінде көз жеткізуге болады.
ІX
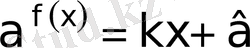 түріндегі теңдеу, айнымалының мәндерін іріктеп, таңдап алу нәтижесінде немесе графиктік тәсілдің көмегімен шешіледі. Ол үшін
түріндегі теңдеу, айнымалының мәндерін іріктеп, таңдап алу нәтижесінде немесе графиктік тәсілдің көмегімен шешіледі. Ол үшін
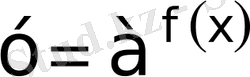 және
және
 функцияларының графиктерін бір координата жазықтығында саламыз. Олардың қиылысу нүктесі, теңдеудің шешімі болады.
функцияларының графиктерін бір координата жазықтығында саламыз. Олардың қиылысу нүктесі, теңдеудің шешімі болады.
Мысалы. Теңдеуді шешіңіз
42)

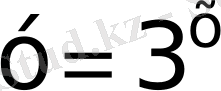 және
және
 функцияларының графиктерін салып, олардың қиылысу нүктелерін анықтайық
функцияларының графиктерін салып, олардың қиылысу нүктелерін анықтайық
 а)
а)
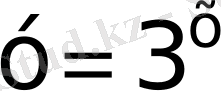
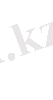
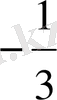
б)

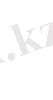 -1
-1
Функциялардың мәндерінің х= 0 және x= 1 нүктелерінде теңесетіндігін байқаймыз, яғни бастапқы теңдеу түбірлері х= 0, x= 1
Қайталауға арналған сұрақтар
- Бүтін көрсеткішті дәреженің қасиеттерін атаңыз
- Бөлшек корсеткішті дәреже қасиеттерін атаңыз
- Көрсеткіштік функция және оның басты қасиеттерін атаңыз
- aх=bтүріндегі теңдеудіңb-ның қандай мәнінде
а) шешімі болмайды
б) жалғыз ғана шешімі болады
в) екі немесе одан да көп шешімдері болуы мүмкін бе?
- Біртекті көрсеткіштік теңдеулерді шешу тәсілін еске түсіріңіз
- Көрсеткіштік теңдеулерге логарифмдеу тәсілін қай кезде қолдануға болады?
- түріндегі теңдеулерді шешу тәртібін айтыңыз
- Көрсеткіштік теңдеулерде көмекші айнымалыны қандай жағдайда еңгізуге болады?
- Графиктік тәсілді қандай жағдайда қолдануға болады?
- а-ның қандай мәніндетеңдеуінің жалғыз ғана шешімі болады?
Тест тапсырмалар
- Есептеңіз
А)
 В) 5 С) 25 D) 125 Е) 625
В) 5 С) 25 D) 125 Е) 625
- Өрнекті ықшамдаңыз
А)
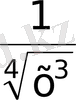 В)
В)
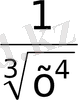 С)
С)
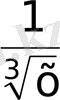 D)
D)
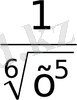 Е)
Е)
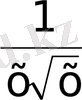
- - сандарының өсу бағытында орналастырыңыз
А)
 В)
В)
 С)
С)

D)
 Е)
Е)

- Теңдеуді шешіңіз
А)
 В) -4, 8 С) -1 D)
В) -4, 8 С) -1 D)
 Е) log
5
2
Е) log
5
2
- Теңдеуді шешіңіз 9х+32х+1=0
А) 0 В)
 С) -5 D) 1 Е)
С) -5 D) 1 Е)
 Ш
Ш
- Теңдеуді шешіңіз 2х3х+1=81
А) 4, 5 В) 2 С) log
2
9 D) log
6
27 Е)
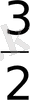 . 3
. 3
- Теңдеуді шешіңіз 32х+3х=12
А)
 В) 1 С) log
3
4 D)
В) 1 С) log
3
4 D)
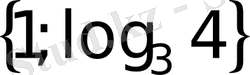 Е)
Е)
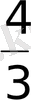
- Теңдеуді шешіңіз 2х+2х+1+2х+2+2х+3=30
А) 0 В) 8 С) 4 D) 2 Е) 1
- 4х+6х=2у9х
А) (1; -2) В) 1 С)
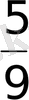 D) 0 Е)
D) 0 Е)
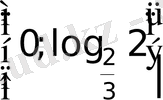
- Теңдеуді шешіңіз 2х+1Һ5х=200
А) 3 В) 2 С) 1 D) log 2 10 Е) log 5 10
- Теңдеуді шешіңіз
А) 1 В) 2 С) 0 D) -2 Е) -1
- Теңдеуді шешіңіз 52х-7х+35Һ52х-35Һ7х=0. 3
А) 2 В) 1 С) 0 D) -1 Е) log 25 7
- 3х=x+7 теңдеудің төмендегі тәсілдердің қайсысымен шығарған тиімді
А) Анықтамаға сүйеніп
В) Көмекші белгісіз еңгізу
С) Логарифмдеу
D) Графиктік тәсіл
Е) Әрбір қосылғышты жеке-жеке нольге теңестіріп
- Теңдеуді шешіңіз
А)
 В)
В)
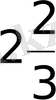 С) 1, 5 D) -0, 5 Е) 0, 25
С) 1, 5 D) -0, 5 Е) 0, 25
- Теңдеудің түбірлері көрсетілген аралықтың қайсысында жатады
А) (0; 3) В) (-1; 5) С) (-2; 4) D) (-2; 3) Е) (-1; 1)
- Теңдеуді шешіңіз 525456… 52х=0, 04-28
А) 9 В) 7 С) 5 D) 6 Е) 8
- Теңдеуді шешіңіз
А)
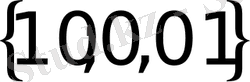 В)
В)
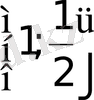 С)
С)
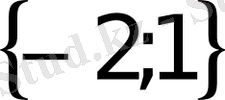 D)
D)
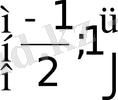 Е) 1
Е) 1
- Теңдеуді шешіңіз 52х-1= 73-х
А)
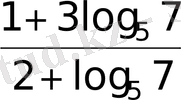 В)
В)
 С)
С)
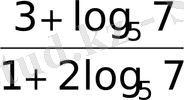
D)
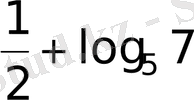 Е)
Е)
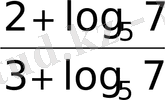
- Теңдеуді шешіңіз
А) lg3 В) lg27 С) 3 D)
 Е)
Е)
 Ш
Ш
- Теңдеуді шешіңіз
А) 1 В)
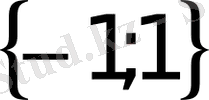 С) 2 D)
С) 2 D)
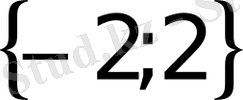 Е)
Е)
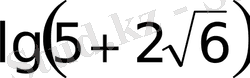
Бақылау тапсырмалары
Теңдеулерді шешіңіз
- теңдеуніңа-ның қандай мәндерінде шешімі бар?
- теңдеуінің жалғыз ғана шешімі бар: оны тауып, оң ба, теріс пе, бірден үлкен бе, кіші ме екенін анықтаңыз
- сандарыа-ның қандай мәнінде, оң мүшелі қайсыбір арифметикалық прогрессияның мүшелері болады?
- Теңдеуді шешіңіз
- Теңдеуді шешіңіз
- Теңдеуді шешіңіз
- Теңдеуді шешіңіз
- Теңдеуді шешіңіз
- Теңдеуді шешіңіз
- Теңдеуді шешіңіз
- Теңдеуді шешіңіз
- Теңдеуді шешіңіз
§2 Логарифмдік теңдеулер
Логарифмдік теңдеу деп айнымалы логарифм белгісінің астында немесе логарифмнің негізінде болатын теңдеулерді айтамыз.
Мысалы
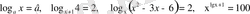 т. с. с.
т. с. с.
Логарифмдік теңдеулерді шешуде негізінен логарифмнің анықтамасына, қасиеттеріне сүйенеміз.
Сондықтан тақырыпты талдамас бұрын логарифм және логарифмдік функцияның қасиеттерін қайталауды оқырманға жүктейміз.
Көрсеткіштік теңдеулер секілді логарифмдік теңдеулерді шешудің жалпыға ортақ ережесі жоқ, бірақ оларды қарапайым тәсілдермен шығарылатын бірнеше түрге топтастыруға болады.
Логарифмдік теңдеулерді шешу барысында бөтен түбірдің пайда болуы мүмкін сондықтан теңдеудің анықталу облысын тапқан немесе табылған түбірлерді бастапқы теңдеуге қойып тексеріп отырған дұрыс. Логарифмдік теңдеулерді шешуде көпшілік жағдайда төмендегі тәсілдер қолданылады:
- Логарифмнің анықтамасына сүйене логарифмдік белгіден құтылу
а)
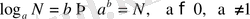 ;
;
б)
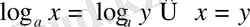 егер
x
>0,
y
>0;
егер
x
>0,
y
>0;
- Көмекші белгісіз еңгізу;
- Теңдіктің екі жағын да логарифмдеу;
- Графиктік тәсіл;
- Мүмкін мәндерді біртіндеп қойып, тексеріп, іріктеп, таңдап алу;
- Әрбір теңдеудің өзіне тән ерекшеліктері негізінде жасанды әдіс амалдар қолдану.
Келтірілген әдіс амалдардың құрылымымен өткен тақырыптарда танысқанбыз.
Енді логарифмдік теңдеудің дербес түрлеріне тоқталайық.
І 1)
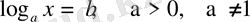 түріндегі теңдеудің шешімі
түріндегі теңдеудің шешімі
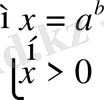 жүйеден анықталынады. Мұнда
x
>0 теңсіздігінің шешімі теңдеудің анықталу облысы болады.
жүйеден анықталынады. Мұнда
x
>0 теңсіздігінің шешімі теңдеудің анықталу облысы болады.
2)
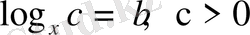 түріндегі теңдеудің шешімі
түріндегі теңдеудің шешімі
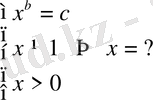 мұнда
мұнда
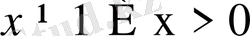 теңсіздіктері логарифмнің анықтамасынан туындайды, яғни логарифмнің негізі бірден өзгеше және оң сан болуы қажет.
теңсіздіктері логарифмнің анықтамасынан туындайды, яғни логарифмнің негізі бірден өзгеше және оң сан болуы қажет.
3)
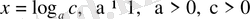 - түріндегі теңдеу, логарифмдік теңдеу емес, бірақ көпшілік жағдайда логарифмнің қасиеттері негізінде ықшамдалып, шығарылады.
- түріндегі теңдеу, логарифмдік теңдеу емес, бірақ көпшілік жағдайда логарифмнің қасиеттері негізінде ықшамдалып, шығарылады.
Мысалдар. Теңдеулерді шешіңіз
Бірақ логарифм астындағы сан оң сан болуы қажет, бұдан х =-2 бөтен түбір. Жауап х =2
Логарифмнің негізі оң сан болуы қажет, яғни х =-2 бөтен түбір. Жауап х =2.
6)
 - бөтен түбір. Жауап
- бөтен түбір. Жауап
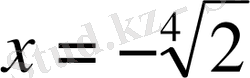 немесе яғни теңдеудің анықталу облысын табатын болсақ
немесе яғни теңдеудің анықталу облысын табатын болсақ
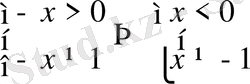
Табылған шешім
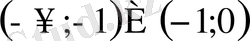 аралығында жатуы қажет. Бұл шартты екінші түбір қанағаттандырады.
аралығында жатуы қажет. Бұл шартты екінші түбір қанағаттандырады.
7)
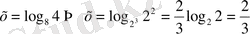
8)
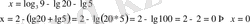
9)
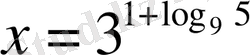

10)
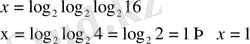
ІІ
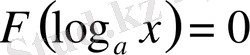 немесе
немесе
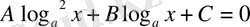 түріндегі теңдеулер.
түріндегі теңдеулер.
Мұнда F (*) кез келген күрделі рационал функция, A, B, C - const
Егер теңдеудегі айнымалыны өзінің құрамында ұстайтын логарифмдік өрнектердің негіздері де, логарифм астындағы шамалары да бірдей болса, көмекші белгісіз еңгізу нәтижесінде теңдеуді ықшамдайық, яғни
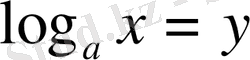 деп белгілсек
деп белгілсек
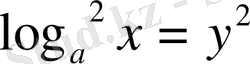 болады. Бұдан
болады. Бұдан
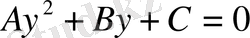 квадрат теңдеуді шешіп, табылған мәндерін пайдаланып, бастапқы айнымалыға қайта көшсек, берілген теңдеуге эквивалентті теңдеулер аламыз.
квадрат теңдеуді шешіп, табылған мәндерін пайдаланып, бастапқы айнымалыға қайта көшсек, берілген теңдеуге эквивалентті теңдеулер аламыз.
Мысалдар. Теңдеулерді шешіңіз
11)
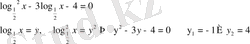
а)
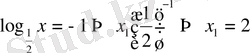
б)
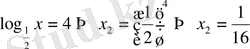 Жауап
Жауап
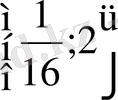
12)
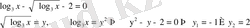 Equation. 3
Equation. 3
а)
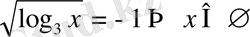 Equation. 3
Equation. 3
б)
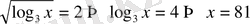 Equation. 3
Equation. 3
13)
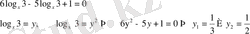 Equation. 3
Equation. 3
а)
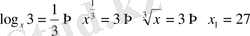 Equation. 3
Equation. 3
б)
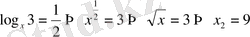 Equation. 3 Жауап
Equation. 3 Жауап
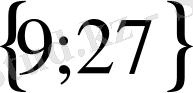 Equation. 3
Equation. 3
ІІІ
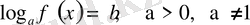 Equation. 3 - түріндегі теңдеу.
Equation. 3 - түріндегі теңдеу.
Теңдеудің анықталу облысы
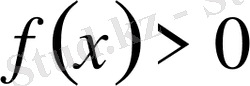 Equation. 3 теңсіздігінің шешімі болады. Бұл түрдегі теңдеудің шешімі
Equation. 3 теңсіздігінің шешімі болады. Бұл түрдегі теңдеудің шешімі
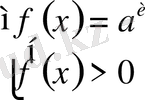 Equation. 3 жүйесінің шешімі болады немесе
Equation. 3 жүйесінің шешімі болады немесе
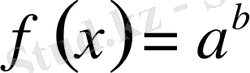 Equation. 3 теңдеуінің түбірін тауып бастапқы теңдеудің анықталу облысына жататынын не жатпайтынын анықтаса жеткілікті.
Equation. 3 теңдеуінің түбірін тауып бастапқы теңдеудің анықталу облысына жататынын не жатпайтынын анықтаса жеткілікті.
Мысалдар. Теңдеулерді шешіңіз
Екі түбір де теңдеуді қанағаттандырады.
15)
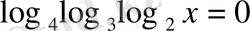 Бұл мысалда
Бұл мысалда
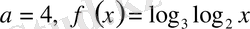 деп түсінеміз, демек
деп түсінеміз, демек

Бұдан
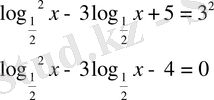
Тапсырманы аяқтау оқырманға жүктелінеді. Жауап
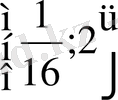
ІV
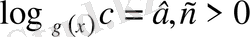 Equation. 3 түріндегі теңдеу. Мұнда
Equation. 3 түріндегі теңдеу. Мұнда
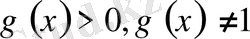 Equation. 3 рационал функция.
Equation. 3 рационал функция.
Бұл теңдеудің шешімі
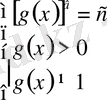 Equation. 3 жүйесінің шешімімен пара-пар немесе
Equation. 3 жүйесінің шешімімен пара-пар немесе
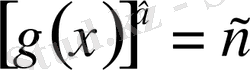 Equation. 3 теңдеуінің түбірлерін тауып, олардың ішінен бастапқы теңдеуді іріктеп алса жеткілікті.
Equation. 3 теңдеуінің түбірлерін тауып, олардың ішінен бастапқы теңдеуді іріктеп алса жеткілікті.
Мысалдар. Теңдеулерді шешіңіз
Бірінші түбір бөтен түбір, себебі х =-1-де логарифмдік өрнектің негізі теріс мән қабылдайды. Жауап х =3.
18)
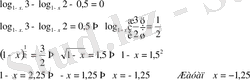
19)
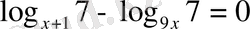
Логарифмдік теңдеулерді шешуде басты назарды негізіне аударамыз, егер негіздері әртүрлі болса, қажетті түрлендірулер жасап бірдей түрге келтіреміз. Берілген теңдеуде логарифмдік өрнектердің негіздері әртүрлі, демек
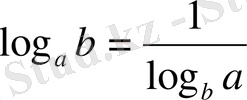
формуласына сүйеніп, теңдеудегі логарифмдік өрнектерді 7 негізіне көшіреміз
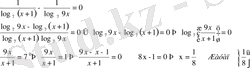
V
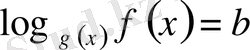 түріндегі теңдеу, мұнда
түріндегі теңдеу, мұнда
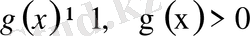 және
және
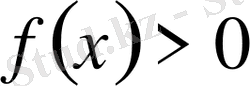 рационал функциялар. Бұл теңдеудің шешімі
рационал функциялар. Бұл теңдеудің шешімі
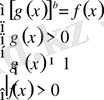
жүйенің шешімімен анықталынады.
20)
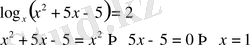
Бірақ табылған түбір теңдеуді қанағаттандырмайды, себебі
 және
және
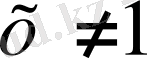 болуы қажет, яғни
х
=1 бөтен түбір. Жауап
болуы қажет, яғни
х
=1 бөтен түбір. Жауап

21)
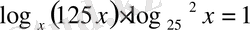
Логарифмдік өрнектердің негіздері әртүрлі
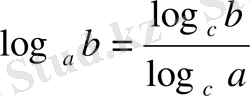
бір негізден екінші негізге көшу формуласына сүйеніп, логарифмдік өрнектерді 5 негізіне көшірейік
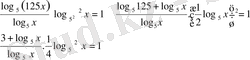
Есепті аяқтау оқырманға жүктелінеді.
VІ
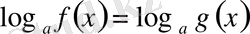 түріндегі теңдеу. Мұнда
түріндегі теңдеу. Мұнда
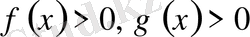 Equation. 3 оң мәнді рационал функциялар. Бұл теңдеу
Equation. 3 оң мәнді рационал функциялар. Бұл теңдеу
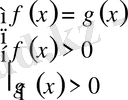 Equation. 3 жүйеге келтіріледі.
Equation. 3 жүйеге келтіріледі.
Мысалдар. Теңдеулерді шешіңіз
22)
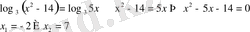 Equation. 3
Equation. 3
Бірінші түбір бөтен түбір. Жауап

23)
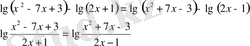
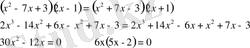
а)
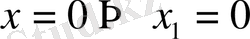 б)
б)
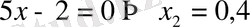
Екі түбір де берілген теңдеуді қанағаттандырмайды.
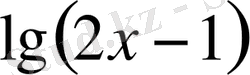 - өрнегіндегі логарифм астындағы шама
х
=0 және
х
=0, 4 мәндеріне теріс санға тең болады, демек олар бөтен түбір. Жауап
- өрнегіндегі логарифм астындағы шама
х
=0 және
х
=0, 4 мәндеріне теріс санға тең болады, демек олар бөтен түбір. Жауап

VІІ
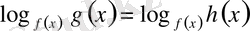 түріндегі теңдеу
түріндегі теңдеу
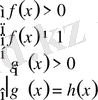 немесе
немесе
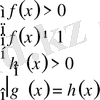
жүйелерінің біріне пара-пар немесе логарифмнің негіздері бірдей болғандықтан логарифм астындағы өрнектерді теңестіріп, алынған теңдеуді шешіп, нәәижесін тексереміз.
Мысалы. Теңдеуді шешіңіз
24)
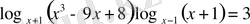
Негіздері әртүрлі, екінші көбейткіштегі логарифмде
х
+1 негізіне көшеміз
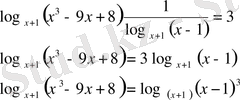
Бұдан
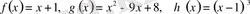 . Теңсіздіктер жүйесін шешкеннен теңдеуді шешіп, нәтижесін тексерген тиімдірек, яғни
. Теңсіздіктер жүйесін шешкеннен теңдеуді шешіп, нәтижесін тексерген тиімдірек, яғни
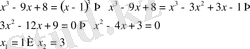
тексерейік
х
=1 бөтен түбір. Жауап
 Equation. 3
Equation. 3
VІІІ
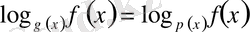 Equation. 3 түріндегі теңдеу.
Equation. 3 түріндегі теңдеу.
Негіздері әртүрлі, бірақ логарифм астындағы өрнектер бірдей. Бүл теңдеу
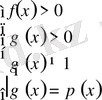 Equation. 3 немесе
Equation. 3 немесе
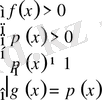 Equation. 3
Equation. 3
теңдеулер жүйесінің біріне пара-пар, яғни
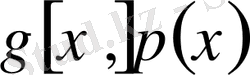 Equation. 3 функцияларының қайсысы қарапайым, соған тәуелді жүйені қарастырамыз.
Equation. 3 функцияларының қайсысы қарапайым, соған тәуелді жүйені қарастырамыз.
Мысалы. Теңдеуді шешіңіз
25)
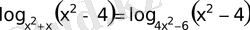
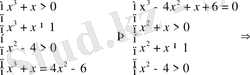
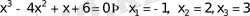
Табылған түбірлердің ішінен жүйені тек х =3 қанағаттандырады. Жауап х =3.
ІX
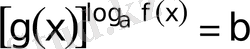 түріндегі теңдеу.
түріндегі теңдеу.
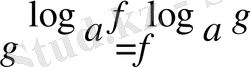
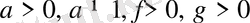 формуласының көмегімен немесе теңдіктің екі жағын да
формуласының көмегімен немесе теңдіктің екі жағын да
 негізде логарифмдеу арқылы шығарылады, яғни
негізде логарифмдеу арқылы шығарылады, яғни
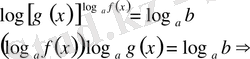 х
-ті тауып нәтижесін тексереміз.
х
-ті тауып нәтижесін тексереміз.
Мысалдар. Теңдеулерді шешіңіз
26)
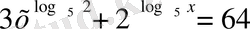
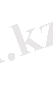
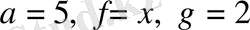
Теңдеудің анықталу облысы
 , осы облыста
, осы облыста
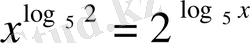
Бұдан берілген теңдеу
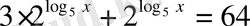 Equation. 3 теңдеуіне пара-пар
Equation. 3 теңдеуіне пара-пар
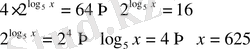
Табылған түбір теңдеудің анықталу облысында жатады. Яғни жауап х =625.
- Теңдіктің екі жағын да 10 негізде логарифмдейміз
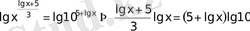
Тапсырманы аяқтау оқырманға жүктелінеді.
Жауап
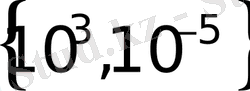 .
.
Қайсыбір (ІX) түрдегі теңдеулер көмекші белгісіз енгізу тәсілімен де оңай шешіледі.
Мысал. Теңдеуді шешіңіз
- Equation. 3 деп белгілесек, х=6уболады. Бұдан
у 1 =-1 және у 2 =1
а)
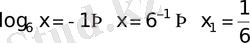
б)
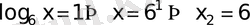 Жауап
Жауап
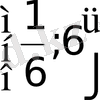
Кейде (ІX) түріндегі теңдеулерді логарифмдік тепе-теңдіктерге сүйеніп шешуге болады, бірақ бұл жағдайларда бөтен түбірдің пайда болмауын қатаң қадағалау керек.
Мысал. Теңдеуді шешіңіз
Берілген теңдеудің анықталу облысы
х
>0 және
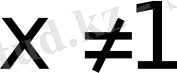 теңсіздіктер жүйесінен тұрады.
теңсіздіктер жүйесінен тұрады.
 формуласына сүйеніп,
формуласына сүйеніп,
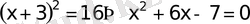 теңдеуін аламыз. Бұдан
теңдеуін аламыз. Бұдан
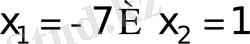 . Бұл екі түбір де теңдеудің анықталу облысында жатпайды, демек
. Бұл екі түбір де теңдеудің анықталу облысында жатпайды, демек
 .
.
X 1)
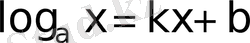 немесе
немесе
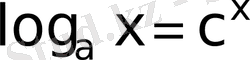 түріндегі теңдеулер.
түріндегі теңдеулер.
Мұнда
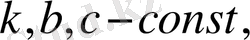
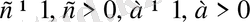 .
.
Екі монотонды өспелінемесе кемімелі функциялардың теңдігінен алынған теңдеулерді.
а)
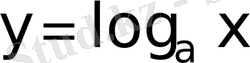 Equation. 3 және
Equation. 3 және
 Equation. 3 немесе
Equation. 3 немесе
б)
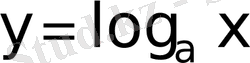 Equation. 3 және
Equation. 3 және
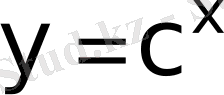 Equation. 3
Equation. 3
функцияларының графиктерінің қиылысу нүктелерін табу арқылы немесе теңдеуді қанағаттандыратын мүмкін мәндерді біртіндеп қойып, тексеріп, таңдап алу нәтижесінде шешеміз.
Мысал. Теңдеуді шешіңіз
30)
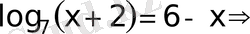 Equation. 3 Жауап
х
=5.
Equation. 3 Жауап
х
=5.
Теңдеудің басқа түбірі жоқ. Себебі
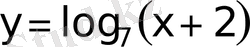 Equation. 3 -өспелі, ал
Equation. 3 -өспелі, ал
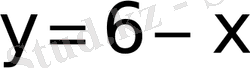 Equation. 3 кемімелі функция, сондықтан олар тек бір ғана нүктеде қиылысады.
Equation. 3 кемімелі функция, сондықтан олар тек бір ғана нүктеде қиылысады.
ҚҚайсыбір теңдеулерді өзіне тән ерекшеліктерді негізінде түрлендіріп, стандартты түрге келтіреміз.
Мысалдар. Теңдеулерді шешіңіз
- егер
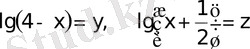 деп белгілесек
деп белгілесек
 екі айнымалыға тәуелді біртекті теңдеу
екі айнымалыға тәуелді біртекті теңдеу
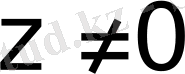 деп, теңдіктің екі жағын
деп, теңдіктің екі жағын
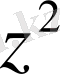 -қа бөлсек, нәтижесінде квадрат теңдеу аламыз немесе көбейткіштерге жіктесек
-қа бөлсек, нәтижесінде квадрат теңдеу аламыз немесе көбейткіштерге жіктесек
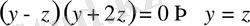 және
және
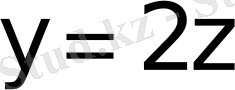 теңдеулерін аламыз.
теңдеулерін аламыз.
Тапсырманы аяқтау оқырманға жүктелінеді.
Жауап
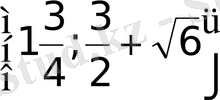
 өрнегіне қатысты квадрат теңдеу ретінде қарастырайық, яғни
өрнегіне қатысты квадрат теңдеу ретінде қарастырайық, яғни
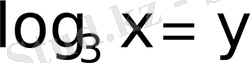 деп белгілесек
деп белгілесек
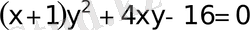 квадрат теңдеу аламыз.
квадрат теңдеу аламыз.
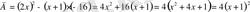 >
>

Демек теңдеудің екі түбірі болады
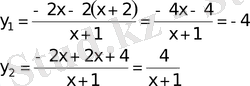
у
айнымалысын табылған мәндермен алмастырсақ, берілген теңдеу
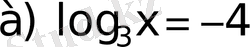 және
және
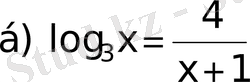 теңдеулеріне жіктелінеді.
теңдеулеріне жіктелінеді.
Тапсырманы аяқтау оқырманға жүктелінеді.
Жауап
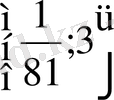
Қайталауға арналған сұрақтар
- Логарифм және оның бастапқы қасиеттерін айтыңыз
- Логарифмді функция және қасиеттерін еске түсіріңіз
- Логарифмдік өрнектерде бір негізден екінші негізге көшу үшін қандай формулалар қолданылады?
- Логарифмдік теңдеу дегеніміз не?
- түріндегі теңдеудің тәуелділігін сипаттаңыз.
- теңдеуініңшексіз көп шешімі болуы мүмкін бе?
- Логарифмдік теңдеулерде көмекші айнымалыны қай жағдайда енгіземіз?
- жәнетеңдеулерінің анықталу облысы қалай табылады?
- Логарифмдік теңдеулерді шешудің негізгі тәсілдерін атаңыз.
- Теңдеу қандай түрде берілсе, логарифмдеу тәсілін қолданамыз?
- Логарифмдік теңдеулерде бөтен түбірді қалай анықтаймыз?
- таңбалары нені білдіреді?
Тест тапсырмалар
- Есептеңіз
А)
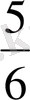 В)
В)
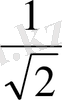 С)
С)
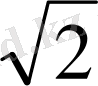 D)
D)
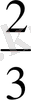 Е)
Е)
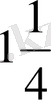
- Есептеңіз
А)
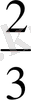 В)
В)
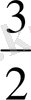 С) 3 D) 2 Е) 1
С) 3 D) 2 Е) 1
- Есептеңіз
А)
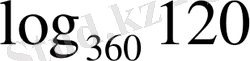 В)
В)
 С)
С)
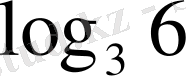 D)
D)
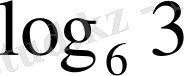 Е)
Е)
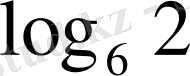
4) Есептеңіз
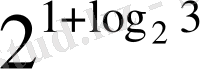
А) 5 В) 6 С) 4 D) 8 Е)
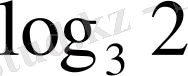
- Есептеңіз
А)
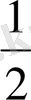 В) 3 С) 2 D) 1 Е) 0
В) 3 С) 2 D) 1 Е) 0
- Теңдеуді шешіңіз
А)
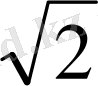 В) 4 С) 16 D) 8 Е)
В) 4 С) 16 D) 8 Е)
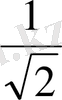
- Теңдеуді шешіңіз
А)
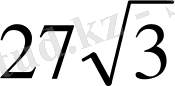 В) 9 С)
В) 9 С)
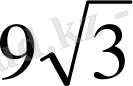 D) 243 Е) 81
D) 243 Е) 81
- Теңдеуді шешіңіз
А) -2 В)
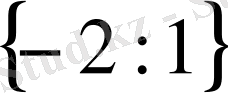 С) 1 D)
С) 1 D)
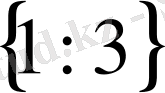 Е)
Е)
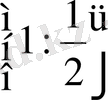
- Теңдеуді шешіңіз
А)
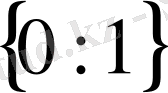 В)
В)
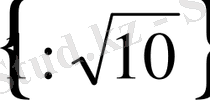 С)
С)
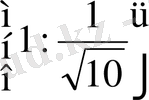 D)
D)
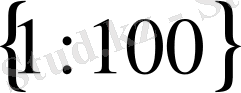 Е) 1
Е) 1
- Теңдеуді шешіңіз
А)
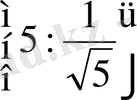 В)
В)
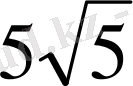 С) 5 D)
С) 5 D)
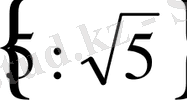 Е)
Е)
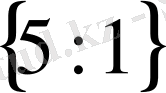
- теңдеуінің түбірі төмендегі сандар жиынының қайсысына жатады?
А) натурал сан В) бөтін теріс сан С) Бөлшек сан
D) иррационал сан Е) нольге тең
- теңдеуінің түбірі көрсетілген аралықтардың қайсысында жатады?
А)
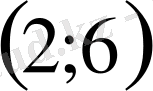 В)
В)
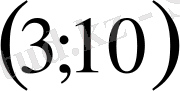 С)
С)
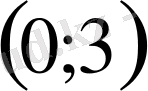 D)
D)
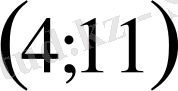 Е)
Е)
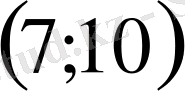
- Теңдеуді шешіңіз
А)
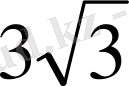 В)
В)
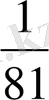 С) 243 D) 27 Е) 81
С) 243 D) 27 Е) 81
- Теңдеуді шешіңіз
А)
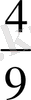 В)
В)
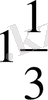 С)
С)
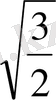 D)
D)
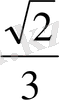 Е)
Е)
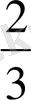
- Теңдеуді шешіңіз
А)
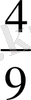 В)
В)
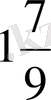 С)
С)
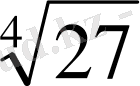 D)
D)
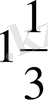 Е)
Е)
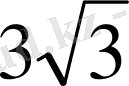
- Теңдеуді шешіңіз
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz