Регрессиялық динамикалық модельдер: стохастық регрессорлар, құралдық өзгергіштер және лагалары үлестірілген модельдерді бағалау


13-Лекция. Регрессиялық динамикалық модельдер
Жоспары:
13. 1. Стохастық регрессорлар.
13. 2. Құралдық өзгергіштер әдісі.
13. 3. Лагалары үлестірілген моделдерді бағалау. Ең кіші еселіктің қарапайым әдісі.
Мақсаты: уақытша қатардың регрессорларының ішінде мағыналарын және стохастық регрессорларды түсіну, құралдық өзгергіштер әдісі арқылы есептер шығару, лагалары үлестірілген модельдерді бағалау және ең кіші еселіктің қарапайым әдісін анықтау болып табылады.
Тақырып бойынша негізгі ұғымдар: Регрессор, стохастық регрессорлар, құралдық өзгергіштер әдісі, лагтық модель, ковариация, уақытша стационарлық қатар, авторегрестік модель, корреляциялық модель, дисперсия, вариация.
Стохастық регрессорлар.
Y=Xβ+ε (13. 1)
Xj - өзгермелілердің мағыналарын алдын-ала таңдаймыз да, осыдан шыққан Y мағыналарын бақылаймыз. Уақытша қатар жағдайында, регрессорлары уақытша трендты, циклдік және маусымдық компоненттерді ұсынатын, түсіндірмелі өзгергіштер де, айқын кездейсоқ емес.
Егер, уақытша қатардың регрессорларының ішінде мағыналарының өзі уақытша қатарды құрайтын өзгергіштер болса, олардың детерминделуі туралы болжау сәйкестікке келмейді. Сондықтан уақытша қатар моделіндегі (t=1, . . . , n; j=1, . . . , p) бақылауларын кездейсоқ өлшемдер деп есептеу керек.
Бұл жағдайда регрессорлар мен ε регрессор қателері арасындағы корреляциялық қатынасы туралы сұрақ туындайды. Осыған бағалау қорытындысы сандық және сапалық жағынан да тәуелді.
xtj және yt - уақытша стационарлық қатар, яғни барлық xt кездейсоқ өлшемдер бірдей үлестіруге тең (және yt -де) .
Қарапайымдылық үшін, бір X регрессоры ғана бар деп алып, яғни модель келесі түрге ие:
yt = α + βxt + εt (13. 2)
(13. 2) теңдігінің екі бөлігінің де xt кездейсоқ өлшемінің ковариациясын қарастырайық:
Cov(x t, y t ) = βCov(x t , x t ) + Cov(x t , ε)
Cov(x t , x t ) = D(x t ) - ескере келіп, келесіні аламыз:
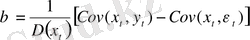 (13. 3)
(13. 3)
(хt, yt - стационарлық қатар болғандықтан, (12. 3) теңдігінің оң жақ бөлігіне жататын коварияция, t-ның барлық мағыналарына сәйкес келеді) . Бұл коварияцияның ішінара бағалауларын қарастырайық:

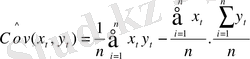
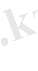 (13. 4)
(13. 4)
(13. 4) және (13. 4) салыстыра келе, β параметрлерін бағалаудың келесідей өрнегін аламыз:

немесе, мұндағы yt = βxt + εt деп алып, келесіні табамыз:
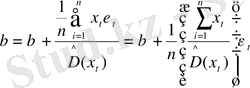 (13. 5)
(13. 5)
Бөлек үш жағдайды қарастырайық:
1. Х регрессорлары мен ε регрессиясы корреляциялық қатынаста болмаған , яғни барлық s үшін бас коварияция Cov (xs, εt), t = 1, . . . , n.
Бұл жағдайда (13. 5) шығатыны:
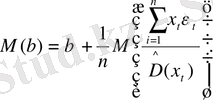
Бұдан өзгеше емес матрицаның күшіне қарай Х және ε және М(ε) = 0, осыдан алатынымыз:
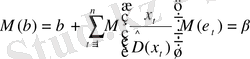 (13. 6)
(13. 6)
яғни b бағалауы бұл жағдайда жылжымаған болып табылады.
Бұл бағалау сонымен қатар тыңғылықты болып табылады. Коварияцияны ішінара бағалау көлемі шексіз артса ықтималдық жағынан оның бас мағынасына сай келеді. Сонымен қатар екі кездейсоқ өлшемнің қатынасының ықтималдық жөнінен шегі олардың шегінің қатынастарына тең, яғни
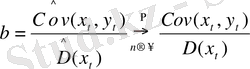
бірақ Cov (xs, εt) болса, онда (13. 3) шығатыны
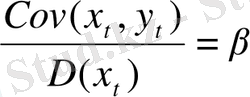 .
.
2. Х регрессорларының мағыналары ε регрессорларының қателерімен берілген уақытта корреляциялық қатынаста болмаған, бірақ регрессия қателерімен ертерек уақытта t - τ корреляциялық қатынаста болған.
Бұл жағдайда (13. 2) бағалауы тыңғылықты болып қалады: дәлелдеуі дәл жоғарыда көрсетілгендей, бірақ жылжымалы емес болмайды.
3. Хt регрессорларының мағынасы εt қателерімен корреляциялық қатынаста .
Бұл жағдайда, тыңғылықтылық және жылжымалы еместікті дәлелдеудің қажеті жоқ. Егер сұрыптау көлемі шексіз артқанымен бірге D(xt) ішінара дисперсиясы шексіз өссе, тыңғылықтылық сақталуы мүмкін, бірақ бұл жағдайда әр нақты міндет жеке талдауды қажет етеді.
Сонымен, егер стохатикалық регресорлары бар модель кездезсе,
Y=Xβ+ε
онда β параметрлерінің ең кіші еселік әдісімен алынған бағалауы:
жылжымалы емес және тыңғылықты , егер түсіндірмелі өзгергіштер және регрессия қателері корреляциялық қатынаста болмаса;
тыңғылықты, бірақ жылжымалы, егер түсіндірмелі өзгергіштер ертерек уақыттағы регрессия қателерімен корреляциялық қатынаста болса, бірақ бірдей уақытта корреляциялық қатынаста болмаса;
жылжымалы және тыңғылықты емес, егер түсіндірмелі өзгергіштер мен регрессия қателерімен корреляциялық қатынаста бірдей уақытта болса;
Регрессорлар мен регрессия қателерінің арасында жиі кездесетін корреляциялық қатынастарының екі себебін қарастырамыз:
1. ε кездейсоқ мүшесіне де регрессорлар мағынасын қалыптастыратын факторлар әсер етеді.
Мысалы, регрессиялық моделде кездесетін U өзгергішін алсақ
yt = α + βxt + γut + vt
xt = λ + δut + ξt
γ және δ коэффиценттері нолден біршама өзгешеленеді. (Қарапайымдылық үшін кездейсоқ өлшем ретінде алынған тек бір ғана Х регрессоры бар деп аламыз) .
U бақыланатын мағынасы жоқ деп алып, келесі моделді қарастырамыз:
yt = α + βxt + εt.
Бұл жағдайда Х регрессорларының және регрессия қателерінің ε (Cov(X, ε) = γδ Cov (U, U) ) корреляциялық қатынастарын күтеміз.
Келесі моделді мысалды қарастырайық.
А поселкесінде екі түрлі шикізат өндіріледі I және II. Шикізат В қаласына жеткізіліп, мұнда зауытта өнім өндіріліп, өндіруші-фирмаға Х бағасымен сатылады. Бұл өнімнен фирма ақырғы тауар әзірлеп аудан орталығына Y бағамен сатылады. Бірінші және екінші түрлі тауар бағалары өзгеріп, уақытша Z1 және Z2 қатарын құрайды.
Өндіруші фирма Y және Х бағаларының арасында тәуелділік орнату мақсатында келесідей регресстік модельді қарастырады
yt = α + βxt + εt
Эксперименталды берілгенге ең кіші еселік әдісін қолдану келесі нәтижені береді:
yt = 13, 64 + 1, 415 xt, d = 2, 14, R²= 0, 96. (13. 7)
(4, 82) (0, 01)
Алынған нәтиже қаншалықты ақиқатқа сай келеді? Шикізатты В қаласына жеткізу де, және ақырғы тауарды С қаласына жеткізу де тасымалдауға байланысты, яғни жанар жағар майға кеткен шығын, жүргізушілер жалақысы, жолдардың күйі т. б. факторларға байланысты Х бағасын қалыптастыруда, және Y ақырғы тауар бағасын, яғни моделдің регрессия қателерінің көлеміне әсер етеді. Сонымен, регрессорлар мен регрессия қателері корреляциялық қатынаста болып табылады, жәнеде ең кіші еселік әдісімен алынған бағалаулар, тыңғылықсыз болып табылады.
2 . Регрессорларды өлшеудегі қателер . Хj регрессорын өлшеуде М(utj) =0 шартын қанағаттандыратын Uj кездейсоқ қатесі жіберілген болса, өңдеуге хtj бақылаудың ақиқат мағынасы емес, бұрмаланғаны түседі
(хtj) * = хtj + utj .
Моделді бағалауда факт жүзінде регрессиясы қарастырылады:
Y = Xβ + v.
Дәл осы теңдіктен біз β бағасын аламыз.
Ал шындығында да,
Y = Xβ + ε = (X* - U) β + ε = X*β + (ε - Uβ)
яғни v = ε - Uβ, осыдан шығатыны факт жүзінде қарастырылған моделде Х* регрессия мағыналары мен v кездейсоқ мүше арасында корреляция бар: Cov(X*, v) = - Cov(U, U) β.
Көрсетілген регресорлар мен регрессия қателерінің арасындағы корреляциялық қатынастың екі түрлі себебінің математикалық мәні бірдей.
Құралдық өзгергіштер әдісі.
Бұл әдістің негізгі ойы (13. 1) теңдігіндегі ε корреляциялық қатынасқа түспейтін, ал Хj тығыз корреляциялық қатынасқа түсетін Zj(j=1, . . . , l ) жаңа өзгергіштерді таңдап алу болып табылады. {Zj} өзгергіштің жиынтығы ε корреляциялық қатынасқа түспейтін регрессорлардан және басқа да өлшемдерден тұрады. {Zj} өзгергіштердің саны регрессорлардың бастапқы санынан айырмашылығы болуы мүмкін.
Мұндай өзгергіштер Z1, . . . , Zе құралдық деп аталады.
Олар (13. 1) моделінің β параметрінің тыңғылықты бағалауын құруға мүмкіндік береді. Ондай бағалау келесі түрдегідей:
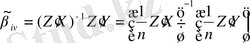
 (13. 8)
(13. 8)
Мұндағы Z, X, Y - өзгергіштердің бақылау мағыналарының матрицасы.
Егер жұптық модель қарастырылса, және жалғыз Х өзгергіші жалғыз құралдық өзгергішпен алмастырылса, онда (13. 8) формуласы келесі түрге ие болады:
 (13. 9)
(13. 9)
Егер zt қатары - стационарлық болса, бұдан кездейсоқ zt өлшемдері біркелкі үлестірілген болса, онда (13. 9) формуласы келесі түрде жазылады.
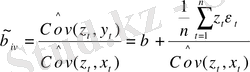 (13. 10)
(13. 10)
Z пен ε корреляциялық қатынасқа түспейтіндіктен, (13. 10) теңдігі β̃iv тыңғылықты болып табылады. Сонымен қатар (13. 10) теңдігінен β̃iv бағалауының жылжымалы еместігі шықпайды. Бұл бағалау минималды коварияцияға да ие емес. Негізінде β̃iv айқын Z тәуелді. Минималды коварияцияға ие болған бағалау, жалғыз болып табылады.
Ең жақсы құралдық өзгергішті қалай таңдауға болады деген сұрақ туындайды, яғни β̃iv бағалауы ең кіші коварияцияға ие өзгергішін таңдау. Бұл міндетті шешудің негізі болып, келесі теорема табылады.
Теорема. Сұрыптау көлеміні шексіз артса, р-мөлшерлі β̃iv кездейсоқ өлшемін үлестіру β қалыпты математикалық күту мен коварияциялық матрицаға, (RR) ˉ¹ пропорционалды матрицаға, мұндағы R - Z құралдық өзгергіш пен Х бастапқы өзгергіш арасындағы корреляционды матрицаға ұмытылады.
Мұндағы р - бастапқы регрессор саны; l - құралдық өзгергіштер саны
( l ≥ р ) ; R матрицасы l *p өлшеміне ие;
Сонымен, Х бастапқы өзгергіштер мен Z құралдық өзгергіштер неғұрлым тығыз корреляциялық қатынаста болса, соғұрлым β̃iv бағалаудың тиімділігі артады. Бірақ бұл жағдайда Cov (Z, ε) = 0 шарты орындалуы тиіс. Осыдан шығатын оптималды құралдық өзгергіш болып, келесі түрдегі өзгергіштер табылады:
Z*j = Xj - Мε(Xj), j = 1, . . . , р.
Мұндағы Х, Z - р-мөлшерлі кездейсоқ өлшемдер.
Бірақ кездейсоқ Z* кездейсоқ өлшемі бақыланбайды . Сонымен осыдан жақсы құралдық өзгергіштер жиынтығы жоқ .
Анық экономикалық мәні бар, {Zj} құралдық өзгергіштердің жеке дара жиынтығы бар, олардың саны р - Xj бастапқы регрессор санынан артық болуы мүмкін. {Z} кеңістігіндегі Xj регрессорларының X̃j проекциясын қарастырайық. Ол үшін келесі түрегі регрессияны жүзеге асыру керек
Xj = Zγ + ν
бұл барлық Xj регрессорлары үшін, және X̃j түсіндірмелі мағынасы үшін
X̃j = Zγ̃ = Z (Z'Z) ˉ¹Z'Xj (13. 11)
X̃j өзгергіші регрессия қателерімен корреляциялық қатынасқа түспейді, себебі құралдық өзгергіш арқылы сызықтық Z1, . . . , Ze сызықтық арқылы түсіндіріледі. X̃j жаңа құралдық өзгергіш ретінде қарастырамыз.
Проекция қасиеттеріне сай X̃'X = X̃' X̃, сонымен β̃iv бағалауы келесі түрді қабылдайды:
β̃iv = (X̃' X̃) ˉ¹ X̃'Y (13. 12)
яғни Y = X̃β + ε моделіннің ең кіші еселік әдісі арқылы алынған бағалауына сай келеді.
Баяндалған әрекет екі адымдық ең кіші еселік әдісі деп аталады. Мұнда ең кіші еселік әдісі екі рет қолданылады: алдымен Х регрессорларының жиынтығын алу үшін, β параметрінің бағалауын алу үшін.
(13. 11) -ді (13. 12) -ге қойып, Z бастапқы құралдық өзгергішінің екі адымдық ең кіші еселік әдісі арқылы бағаланған өрнегін аламыз:
β̃iv = (X'Z(Z'Z) 'Z'X) ˉ¹X'Z(Z'Z) ˉ¹Z'Y (13. 13)
Екі адымдық ең кіші еселік әдісі көбіне компьютерлік регрессиялық пакеттерде кеңінен таралған.
Лагалары үлестірілген моделдерді бағалау. Ең кіші еселіктің қарапайым әдісі.
Жоғарыда айтылғандай, уақытша қатар моделінде жиі түсіндірмелі өзгергіштердің мағыналары олардың алдыңғы уақыттағы мағыналарына байланысты деп айтқанбыз.
Авторегрестік модель деп р және q қатарларының лагалары үлестірілген келесідей түрдегі модель аталады:
yt = α + β0xt + β1xt-p + . . . + γ1yt-1 + . . . + γqyt-q +εt. (13. 14)
Бұндай жағдайда yt-τ және εt арасында корреляциялық қатынас болады.
Дәл осы моделдердің көбіне тәжірибелік мағынасы бар және регрессор мен регрессиялық қателер арасындағы пайда болатын дәл осындай корреляция экономикалық қосымшаларында кездеседі. Тәжірибеде (0, 1) қатарлы ADL моделі жиі пайда болады, яғни келесі түрдегі модель:
yt = α+βxt+γyt-1+εt (13. 15)
AR (1) қатарлы авторегрессорлық процеске, εt регрессиясының қателерімен және МА (1) бірінші қатарлы өтпелі орташаның заңына тәуелді:
εt=ρεt-1+ξt; (13. 16)
εt=ξt+ρξt-1. (13. 17)
Екі жағдайда да ξt - тәуелсіз, бірдей үлестірілген кездейсоқ нолдік математикалық тосуы және σ² дисперсиясы бар өлшемдер.
(13. 15) моделінен бастайық. Қарапайымдылық үшін (13. 15) теңдігінде Х регрессоры жоқ деп алып, яғни yt-1 өзгергіш лага жалғыз түсіндірмелі өзгергіш болып табылады деп алсақ, модель келесі түрге ие:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz