Электрохимия. Электролит ерітінділері

Мазмұны

1. Активтік және активтік коэффициент . . . 2Активтік коэффициенттің концентрацияға тәуелділігі. Иондық күш . . . 6Күшті электролиттердің Дебай-Гюккель теориясы . . . 8Дебай-Гюккель теориясының теңдеулері. Активтік коэффициентінің анықталуы . . . 10
2. Электролиттердің электрөткізгіштігі . . . 16
3. Тасымалдау саны . . . 20
4. Пайдаланған әдебиеттер . . . 28

Электрохимия. Электролит ерітінділері.

Мақсаты: Активтілік коэффициентін, электр өткізгіштікті және ауысу сандарын есептеуді үйрену.

Тапсырмалар:
*активтілік коэффициентін;
*электр өткізгіштікті;
*ауысу сандарын есептеу.

1. Активтік және активтік коэффициент.

Идеал ерітінділердің теңдеулеріне қысым орнына ұшқыштықты (немесе фугитивтікті), концентрация орнына активтікті қойса (Льюистің активтік теориясы бойынша), ол теңдеулерді реал ерітінділердің қасиеттерін сипаттауға қолдануға болатындығы белгілі. Әлсіз электролиттердің диссоциациялану константасы теңдеуіндегі (1) концентрация орнына активтікті қойсақ:

K=C _H3O ⁺ ∙ C _CH3COO ^- /C _CH3COOH (1)

K _a = (a ₊ ∙ a _- ) / a _a (2)

Мұнда a ₊ және a _- - катион және анион активтіктері. a _a - электролиттің диссоциацияға ұшырамаған молекулаларының активтігі. Осы (2) -теңдеу арқылы есептелген диссоциациялану константасының мәні реал ерітінділер (күшті электролиттер және әлсіз электролиттердің жоғары концентрациялы ерітіндісі) үшін тұрақты шама болады. Активтік пен концентрацияның айырмашылығы реал ерітіндінің идеал ерітіндіден айырмашылығын көрсетеді. Электролит ерітіндісінде иондар арасында және ион мен еріткіш арасында байқалатын әр түрлі әрекеттестіктердің нәтижесінде ерітіндідегі барлық бөлшектердің саны бастапқы ерітілген молекулалар санынан басқаша болады. Бастапқы еріген молекулалар санын аналитикалық концентрация көрсетсе, ерітіндідегі бөлшектердің нақты санын активті концентрация (активтік) көрсетеді. Осыған байланысты реал ерітіндінің қасиеті (бөлшектердің нақты санымен анықталатындықтан) идеал ерітінді қасиетінен ауытқиды. Ауытқудың шамасын активтік коэффициент көрсетеді. Льюис теориясы бойынша, ерітіндінің активтігі аналитикалық концентрациясын активтік коэффициентке көбейткенге тең:

a _C =ɣ _C ∙C; a _m =ɣ _m ∙m; a _N =ɣ _N ∙N (3)

Мұнда ɣ _C - мольдік, ɣ _m - молялдық, ɣ _N - рационалдық активтік коэффициенттері; С - мольдік, m - молялдық, N - мольдік үлеспен алынған концентрациялар.

Сөйтіп, активтік пен концентрацияның бір-бірінен айырмашылығын көрсететін шама активтік коэффициент болып табылады.

Активтік коэффициент заттың бір молінің реал ерітіндіден идеал ерітіндіге көшуі үшін жұмсалатын энергияның (жұмыстың) өлшемі. Электролит ерітінділерінің идеал ерітіндіден ауытқуы бөлшектер арасындағы әрекеттесу күштерінің энергиясымен анықталатындықтан, активтік коэффициент пен осы энергия арасындағы байланыс жалпы термодинамикалық заңдылықтардан шығады. Мысалы, берілген ионның реал ерітіндідегі химиялық потенциалы:

µ _i = µ _i ⁰ +RTlna _i = µ _i ⁰ +RTlnC _i +RTlnɣ _i ,

идеал ерітіндідегі потенциалы:

µ _i ^ud =µ _i ⁰ +RTlnC _i

Осыдан

µ _i - µ _i ^ud =RTlnɣ _i ,

немесе

lnɣ _i =(µ _i - µ _i ^ud ) / RT (4)

Ал

µ _i - µ _i ^ud = g _i ^* , (5)

g _i ^* - берілген ионның ертіндіде өз айналасындағы бөлшектермен әрекеттесу энергиясы. (4) және (5) - теңдеулерден

lnɣ _i = g _i ^* / RT (6)

Бұл (6) - теңдеу ерітіндіде әрекеттесу күштері артқан сайын оның идеал ерітіндіден ауытқуы да артып, активтік коэффициенттің мәні 1-ден көп өзгеше болатынын көрсетеді.

Активтік пен активтік коэффициентті әрбір жеке ион үшін анықтауға болмайды. Себебі активтікті анықтайтын теңдеулер жеке ионның емес, ерітіндідегі барлық иондардың (катиондар және аниондар) активтіктерінің көбейтіндісі арқылы жазылады. Сол себепті орташа иондық активтік а _+- және орташа иондық активтік коэффициенті ɣ _+- дейтін ұғымдар енгізілді. Егер берілген электролиттің ерітіндісінде катиондар саны ν ₊ , аниондар саны ν _- болса, ерітіндінің орташа иондық активтігі мына формуламен өрнектеледі:

a _± =(a ₊ ^ν+ ∙ a _- ^ν- ) ^1/ν , (ν= ν ₊ + ν _- ) (7)

Демек, орташа иондық активтік дегеніміз ерітіндідегі барлық иондар активтіктерінің геометриялық орта шамасы. Бинарлы электролит үшін (7) - теңдеу мына түрде жазылады:

a _± =(a ₊ ∙ a _- ) ^1/2 = $\sqrt{a_{+} \bullet a_{-}}$ $\sqrt{a_{+} \bullet a_{-}}$ (8)

Электролиттің орташа иондық активтік коэффициенті де дәл осылай анықталады:

ɣ _± =(ɣ ₊ ^ν+ ∙ ɣ _- ^ν- ) ^1/ν , (9)

бинарлы электролит үшін:

ɣ _± =(ɣ ₊ ∙ ɣ _- ) ^1/2 = $\sqrt{ɣ_{+} \bullet ɣ_{-}}$ $\sqrt{ɣ_{+} \bullet ɣ_{-}}$ (10)

Жоғарыда айтылғандарды концентрация үшін де қолдануға болады. Ерітіндінің орташа молярлық концентрациясы:

m _± =[( ν ₊ m ₊ ) ^ν+ ( ν _- ∙ m _- ) ^ν- ] ^1/ν , (11)

ал бинарлы электролит үшін:

m _± =(m ₊ ∙ m _- ) ^1/2 = $\sqrt{m_{+} \bullet m_{-}}$ $\sqrt{m_{+} \bullet m_{-}}$ (12)

Сонда орташа иондық активтік:

a _± =m _± ∙ ɣ _± =[( ν ₊ m ₊ ) ^ν+ ( ν _- m _- ) ^ν- ] ^1/ν (ɣ ₊ ^ν+ , m ∙ ɣ _- ^ν- , m) ^1/ν (13)

бинарлы электролит үшін:

a _± = $\sqrt{m_{+}ɣ_{+}\ \bullet \ m_{-}\ ɣ_{-}\ \ \ \ }$ $\sqrt{m_{+}ɣ_{+}\ \bullet \ m_{-}\ ɣ_{-}\ \ \ \ }$ (14)

Электролит ерітіндісінің активтігі оның концентрациясы мен орташа активтік коэффициент арқылы былай жазылады:

a _C =C∙ ɣ _± , _C ; a _m =m∙ ɣ _± , _m ; ; a _N =N∙ ɣ _± , _N (15)

Шексіз сұйылтылған ерітіндіде бөлшектер арасындағы әрекеттесулер өте әлсіз болатындықтан, мұндай ерітіндіде ионның активтігі концентрациясына теңесіп, активтік коэффициент 1-ге тең болады:

(a _C C) _{C 0} ; (a _m m) _{m 0} ; (a _N N) _{N 0} (16)

және

(ɣ _C =ɣ _m =ɣ _N 1) _{C, m, N 0}

Сөйтіп шексіз сұйылтылған (немесе өте төмен концентрациялы ерітінділер үшін ɣ _C , ɣ _m және ɣ _N мәндерінің айырмасы өте аз, сондықтан кейбір есептеу жұмыстарында ɣ _C =ɣ _m =ɣ _N = ɣ деп алынады.

Ерітінділер үшін стандартты күй ретінде шексіз сұйылтылған ерітінді күйін алуға болады. Бірақ шексіз сұйылтылған ерітіндінің концентрациясы анықталмайтын шама, сондықтан ерітінділердің стандартты күйі ретінде концентрациясы, активтігі және активтік коэффициенті бірге тең деп есептелетін жорамал ерітінді алынады. Стандартты ерітінді ретінде алынған біл мольді (С=1) немесе бір молялды (m=1) ерітіндінің активтігі және активтік коэффициенті бірге тең деп есептеледі. Ал егер ерітіндінің құрамы мольдік үлеспен берілсе, онда стандартты ерітінді үшін N=1, a _N =1 және ɣ _N =1. Электролиттің катионы мен анионының стандартты активтіктерінің көбейтіндісі бірге тең, яғни

a ₊ ^ν+ , _станд. ∙ a _- ^ν- , _станд. =1 (17)

деп алынса, онда электролиттің жалпы активтігінің теңдеуі былай жазылады:

a= a ₊ ^ν+ ∙ a _- ^ν- = a _± ^ν , (18)

бинарлы электролит үшін

a=a ² _± , (19)

тернарлы электролит үшін a=a ³ _± , т. с. с.

Бұл (19) -теңдеу толық және жартылай диссоциацияланатын электролиттерге қолданылады. Егер активтік бірге тең болмаса (а≠1), электролиттің жалпы активтігі (а) оның диссоциацияға ұшырамаған молекулаларының активтігіне (а _а ) теңеседі.

Активтік коэффициент арқылы диссоциациялану константасының [(2) -теңдеу] былай жазылады:

K _a =(C _+ɣ+ ∙ C _-ɣ- ) /(C _aɣa ) =[(C ₊ ∙ C _- ) / C _a ] ∙ [(ɣ ₊ ∙ ɣ _- ) / ɣ _a ], (20)

осыдан

K _a =K _C ∙ (ɣ ₊ ∙ ɣ _- ) / ɣ _a , (21)

K _a - термодинамикалық диссоциациялану константасы, ал K _C - классикалық диссоциациялану константасы деп аталады. Мысалы, сірке қышқылының диссоциациялану константасының теңдеуін [(1) -теңдеу] активтік коэффициент арқылы былай жазуға болады:

K _a =[C _H3O ⁺ ∙ C _CH3COO ^- ) /C _CH3COOH ] x[(ɣC _H3O ⁺ ∙ ɣC _CH3COO ^- ) /ɣC _CH3COOH ],

осыдан

K _a =K _C ∙[(ɣ _H3O ⁺ ∙ ɣ _CH3COO ^- ) /ɣ _CH3COOH ], (22)

немесе

pK _a =pK - 2lgɣ ± (CH ₃ COOH) +lgɣCH ₃ COOH (23)

Зарядсыз бөлшектердің (молекула) активтік коэффициенті ионның активтік коэффициентіне қарағанда ерітіндінің концентрациясы өзгергенде өте аз өзгеретіндіктен, және орташа концентрациялы ерітінділер үшін 1-ге жуық болатындықтан (23) -теңдеуді шамамен мына түрде жазуға болады:

pK _a =pK-2lgɣ ± (CH ₃ COOH) (24)

Жоғарыдағы (20) -(24) -теңдеулер диссоциациялану константасының концентрация (К _С ) және (К _а ) арқылы алынған мәндерінің бір-бірімен байланысын көрсетеді. Басқа да химиялық тепе-теңдіктердің идеал және реал ерітінділердегі мәндерінің байланысын дәл осылай көрсетуге болады. Мысалы, сутектік көрсеткіш (рН) реал ерітіндіде сутегі ионы активтігінің теріс ондық логарифміне тең:

pH _a =-lga _H ⁺ (25)

Ал a _H ⁺ =ɣ _H ⁺ ∙ C _H ⁺ , олай болса

pH _a =pH-lgɣ _H ⁺ (26)

Алынған (26) - теңдеу тек сұйылтылған ерітінділерге қолданылады (жоғары концентрациялы ерітінділер үшін иондардың активтік коэффициенттері белгісіз) .

1. 1. Активтік коэффициенттің концентрацияға тәуелділігі. Иондық күш.

Электролит ерітіндісінің активтігі, бейэлектролит заттардың активтігі сияқты, ерітіндінің әр түрлі термодинамикалық қасиеттері (мысалы, ерітіндінің бу қысымы, қату температурасының төмендеуі, электролиттің екі еріткіш арасында таралуы, т. б. ) арқылы анықталады. Сонымен қатар, тек электролиттердің активтігі мен активтік коэффициенттерін анықтау үшін қолданылатын арнайы әдіс - электрқозғаушы күш әдісі бар.

Әр түрлі әдіспен анықталғанына қарамастан активтік коэффициенттің мәні берілген электролит үшін берілген концентрацияда тұрақты болады. 1-кестеде KCl ерітіндісінің әр түрлі концентрациясы үшін үш түрлі жолмен анықталған активтік коэффициенттердің мәндері келтірілген; мұнда ɣ±, 1 - ерітіндінің бу қысымы, ɣ±, 2 - қату температурасының төмендеуі, ɣ±, 3 - электрқозғаушы күші бойынша анықталған активтік коэффициенттер.

(1-кесте)

KCl ерітіндісінің әр түрлі әдіспен

анықталған активтік коэффициенттері

Барлық электролиттер үшін олардың шексіз сұйылтылған ерітінділерінің активтік коэффициенті бірге тең. Ерітіндінің концентрациясы өскенде алғашында активтік коэффициент азайып минимал мәнге жетіп, содан соң қайтадан өседі. Ең жоғары концентрацияларда тіпті бірден көп болуы мүмкін. Төменде MnCl ₂ ерітіндісі үшін әр түрлі концентрациясындағы активтік коэффициенттің мәндері берілген:

Активтік коэффициенттің концентрацияға байланысты өзгеруі иондар арасындағы әрекеттесу күштерімен анықталады. Шынында да, шексіз сұйылтылған ерітіндіде иондар өте аз болатындықтан олардың ара қашықтықтары үлкен, яғни бір-біріне тигізетін әсерлері жоқтың қасы. Бұл кезде ерітінді идеал жүйеге ұқсап, активтігі концентрациясымен теңесіп, активтік коэффициент 1-ге теңеседі (1 және 2-суреттер) .

1-сурет 2-сурет

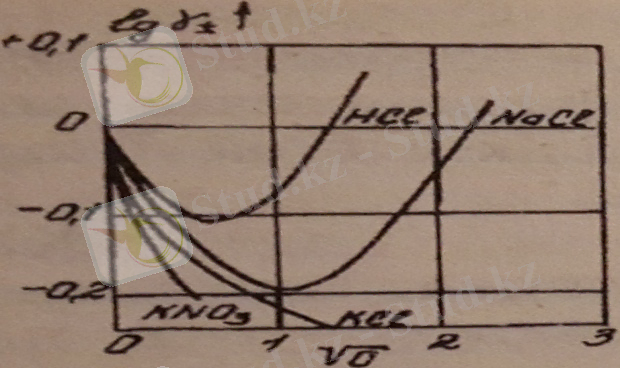
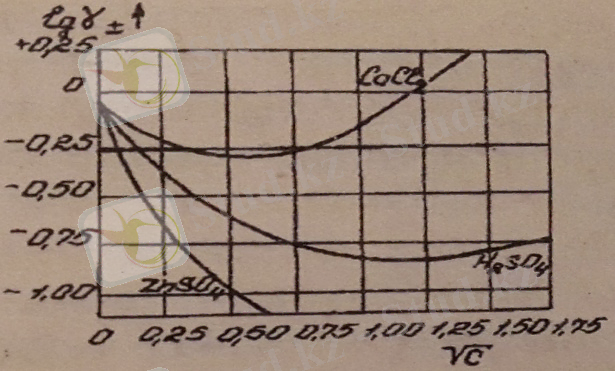
Концентрацияның өсуімен иондар арасы жақындап, олардың бір-біріне тартылыс күштері арта бастайды да, активтік коэффициент бірден төмендейді (а<с) . Концентрацияның белгілі бір мәнінде тартылыс күшімен қатар тербеліс күштері пайда болады. Тартылыс күші мен тербеліс күші теңескен кезде күштер бір-бірін жойып, жүйе идеал жүйеге ұқсайды, активтік коэффициент қайтадан 1-ге тең болады. Концентрацияның өте жоғары мәндерінде тербеліс күші тартылыс күшінен артып, активтік коэффициент 1-ден көп болады (a>c) .

Активтік пен активтік коэффициенттің концентрацияға тәуелділігін зерттеу барысында Льюис және Рендалл бірнеше эмпирикалық заңдылықтар мен ережелерді тапты. Концентрациясы төмен ерітінділерде электролиттің орташа иондық активтік коэффициенті тек иондардың валенттіліктерімен ғана анықталатыны белгілі болды (иондардың қасиеті мен табиғатына тәуелсіз) . Мысалы, калий бромиді, KBr , натрий нитраты NaNO ₃ және тұз қышқылының HCl төмен концентрациялы ерітінділерінің орташа иондық активтік өте сұйылтылған ерітіндіде әр түрлі электролиттердің қоспасы болатын болса, мұндай ерітіндінің орташа иондық активтік коэффициенті ерітіндідегі барлық иондардың тек концентрациялары және валенттіліктерімен анықталып, электролиттердің табиғаттарына тәуелсіз болатындығы белгілі болды.
Осыған байланысты Льюис пен Рендалл ғылымға ерітінділердің иондық күші деген ұғым енгізді. Ерітіндінің иондық күші (I) деп ерітіндідегі барлық ионның (катионның және анионның) концентрациясы мен заряд квадратының көбейтінділерінің жарты қосындысын айтады:

I=(1/2) ∑C _i Z _i ² (27)

Бұл теңдеуден 1-1 валентті электролиттер ерітіндісінің иондық күші ерітіндінің концентрациясына тең, ал басқа типті электролиттер үшін үлкен болатынын көреміз. Мысалы, 2-2 валентті күшті электролиттің С мольдік ерітіндісінің (α=1, C ₊ =C _- =C) иондық күші концентрациясынан 4 есе көп:

I=(1/2) (C∙2 ² +C∙2 ² ) =4∙C

Сонымен қатар, күшті электролиттердің сұйылтылған ерітінділері үшін орташа иондық активтік коэффициенттің логарифмі ерітіндінің иондық күшіне сызықты тәуелділікте болатыны белгілі болды:

lgɣ _± =h $\sqrt{I}$ $\sqrt{I}$ (28)

мұнда h - эмпирикалық тұрақты. Концентрациясы жоғары ерітінділерге (28) -теңдеу қолданылмайды.

2. Күшті электролиттердің Дебай-Гюккель теориясы.

Аррениустың электролиттік диссоциация теориясы тек әлсіз электролиттердің өте сұйық ерітінділеріне қолданылады. Өйткені бұл теория электролит ерітінділерінде болатын ион-ион, ион-молекула арасындағы әрекеттесулерді ескермей, электролит ерітіндісін идеал газдардың қоспасы тәрізді деп қарастырады. Ал электролиттердің термодинамикалық теориясы болса, ол электролит ерітінділерінің идеал ерітіндіден ауытқуын активтік коэффициент арқылы жалпы түрде сипаттағанымен, ауытқудың нақты себептерін, оның қандай күштердің әсерінен болатынын ашып көрсетпейтін формальды теория. Тек XX ғасырдың басында (1923ж) Дебай және Гюккель күшті электролиттердің электростатикалық теориясын ұсынды.

Дебай-Гюккель теориясы мынадай екі жағдайға негізделген: а) күшті электролиттер ерітіндіде толығымен диссоциацияланады (α=1) ; б) күшті электролиттердің идеал ерітіндіден ауытқуы иондар арасындағы электростатикалық күштердің әсерінен болады.

Күшті электролиттер диссоциацияға толық ұшырайтындықтан ерітіндіде иондар көп болып, олардың арасындағы электростатикалық тартылыс не тебіліс күштері күшті болады. Ал әлсіз электролиттердің сұйылтылған ерітінділерінде иондар өте аз болатындықтан олар бір-бірінен үлкен ара қашықтықта орналасып, өзара әсерлері өте аз болады. Осыған байланысты Аррениустың электролиттік диссоциация теориясы әлсіз электролиттердің қасиеттерін жақсы сипаттайды. Иондардың электростатикалық күштің әсерінен бір-біріне тартылуы олардың жеке бөлшек ретінде қозғалысын бәсеңдетеді. Бұл жағдайда күшті электролиттің активтігі оның аналитикалық концентрациясынан кем болады, демек термодинамикалық қасиеттерінің шамасы идеал ерітіндімен салыстырғанда азаяды. Егер де иондардың тартылу күштерінен тебілу күштері артық болса, ерітіндінің активтігі аналитикалық концентрациясынан көп болып, термодинамикалық қасиеттерінің шамасы идеал ерітіндіге қарағанда өседі.

Дебай-Гюккельдің күшті электролиттер теориясы бойынша, электролит ерітіндісінде иондардың орналасуы олардың кристалл торындағы орналасуынан басқаша болады. Индия ғалымы Гхоштың пікірі бойынша (1918-1920ж. ), иондардың кристалдағы орналасу реті ерітіндіде де сақталады делінген. Бірақ ерітінділер құрылысын зерттеудегі көптеген тәжірибелік деректер Гхош пікіріне қайшы келеді. Бұл қайшылықтың басты себебі ерітіндідегі бөлшектердің жылу қозғалыстарын ескермеу болып табылады. Еріткіш молекулаларының жылу қозғалысының әсерінен электролит иондарының кристалл тордағы ретті орналасуы ерітіндіде бұзылып, иондар ерітінді көлемінде шашырап орналасуға тырысады. Екінші жағынан, иондар ерітіндіде электростатикалық күштің әсерінен, керісінше, ретті орналасуға тырысады. Сөйтіп иондардың ерітіндіде орналасуы қарама - қарсы бағытталған осы екі күштің шамаларымен анықталады.

Дебай-Гюккель теориясында ерітіндіде әр ионның төңірегіне электростатикалық күштің әсерінен оған қарама - қарсы зарядталған иондар тартылып шар тәріздес сфера жасай орналасады деп қарастырылады (3-сурет) .

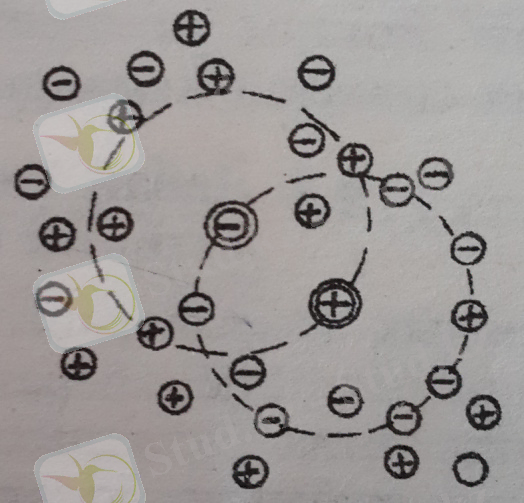
3-сурет

Ерітіндіде иондардың тербелмелі қозғалыстарынан гөрі ілгерілемелі қозғалыстары күштірек иондар бір ионның сферасынан екінші ионның сферасына ауысып, басқа иондармен орын алмастырып отырады. Осындай статистикалық сфераны иондық атмосфера деп атайды. Атмосферадағы кез келген ион орталық ион бола алады, оның төңірегіне де қарсы зарядталған иондардан иондық атмосфера түзіледі. Иондық атмосферада қарсы зарядталған иондармен қатар аттас зарядталған иондар да болады, бірақ қарсы зарядталған иондар көбірек болатындықтан орталық ионның зарядынан иондық атмосфераның заряды артық болады. Иондық атмосфераның түзілуі, оның құрамы мен заряды Максвелл-Больцманның статистикалық заңдарына бағынады. Иондық атмосфераға бір иондар келіп жатса, екінші бір иондар кетіп жатады. Сондықтан да иондық атмосфераның заряды, размері және басқа қасиеттері тұрақты болмай, уақытқа байланысты өзгеріп отырады, олардың тек статистикалық орта мәндері қарастырылады.

Күшті электролиттердің Дебай-Гюккель теориясы электролит ерітіндісінің идеал ерітіндіден ауытқу себебін ерітіндіде иондық атмосфераның түзілуімен, оның размері және зарядының тығыздығымен байланыстыра қарастырады. Иондар арасындағы электростатикалық күштің энергиясы (∆G _эл. ) ретінде иондық атмосфера мен орталық ионның бір-біріне тартылыс күшінің энергиясы алынады.

Сөйтіп күшті электролиттердің Дебай-Гюккель теориясында электролит ерітіндісінде әсер ететін электростатикалық күштер ғана қарастырылады; иондардың еріткіштің молекуласымен әрекеттесуі (сольваттану, гидраттану, т. б. ) мүлде ескерілмейді. Сондықтан да бұл теория күшті электролиттердің электростатикалық теориясы деп аталады. Теория ионның зарядынан басқа қасиеттерін (құрылысы, табиғаты, поляризациясы, т. б. ) есепке алмайды. Ерітіндідегі химиялық күштерді мүлде қарастырмайтындықтан Дебай-Гюккель теориясы физикалық және шектелген теория болып саналады. Бұл теория күшті электролиттердің сұйылтылған ерітінділеріне жақсы қолданылады. Концентрация жоғарылаған сайын бөлшектер арасында химиялық күштердің әсері артатындықтан жоғары концентрациялы ерітінділерді электростатикалық теория сипаттай алмайды.

3. Дебай-Гюккель теориясының теңдеулері. Активтік коэффициентінің анықталуы.

Иондық атмосфераның энергиясы электрлік энергия, сондықтан ол иондық атмосфераның электр зарядының тығыздығы мен потенциалына байланысты. Иондық атмосфераның түзілуі статистикалық құбылыс болатындықтан зарядтардың дискретті таралуын ескермей, заряд тығыздығының (ρ) орташа мәні мен оған сәйкес потенциалдың (ψ) орташа мәні арасындағы байланысты Пуассон теңдеуімен көрсетуге болады:

$\nabla^{2}\psi = ( - 4\pi/D) \rho$ $\nabla^{2}\psi = ( - 4\pi/D) \rho$ , (29)

Мұнда $\pi = 3, 1416;$ $\pi = 3, 1416;$ D - диэлектрлік тұрақты; $\nabla^{2}$ $\nabla^{2}$ - Лаплас операторы, ол тік бұрышты координаталық жүйеде:

$\nabla^{2} = \partial^{2}/\partial x^{2} + \partial^{2}/\partial y^{2} + \partial^{2}/\partial z^{}$ $\nabla^{2} = \partial^{2}/\partial x^{2} + \partial^{2}/\partial y^{2} + \partial^{2}/\partial z^{}$ (30)

Пуассон теңдеуінде екі белгісіз шама бар, олар $\rho\ және\ \psi.$ $\rho\ және\ \psi.$ Бұл шамаларды анықтау үшін олардың байланысын беретін екінші бір теңдеу қажет.

Больцманның статистикалық заңдарын қолданып иондық атмосфераның кез келген нүктесіндегі зарядтың тығыздығын анықтасақ:

$\rho = ( - e^{2}/kT) \sum z_{i}^{2}n_{i}\psi$ $\rho = ( - e^{2}/kT) \sum z_{i}^{2}n_{i}\psi$ (31)

мұнда k - Больцман тұрақтысы; z _i - иондардың заряды; n _i - 1 см ³ көлемдегі иондар саны. Пуассон теңдеуіне ρ мәнін (31) теңдеуден алып қойсақ:

$\nabla^{2}\psi = \left( \frac{4\pi e^{2}}{DkT} \right) \sum z_{i}^{2}n_{i}\psi,$ $\nabla^{2}\psi = \left( \frac{4\pi e^{2}}{DkT} \right) \sum z_{i}^{2}n_{i}\psi,$ (32)

немесе

$\nabla^{2}\psi = \chi^{2}\psi, \$ $\nabla^{2}\psi = \chi^{2}\psi, \$ (33)

мұнда

$\chi = \lbrack(4\pi e^{2}/DkT) \sum z_{i}^{2}n_{i}\psi\rbrack$ $\chi = \lbrack(4\pi e^{2}/DkT) \sum z_{i}^{2}n_{i}\psi\rbrack$ ^1/2 (34)

Бұл теңдеудегі 𝟀, дәлірек айтсақ 1/𝟀 - иондық атмосфераның қалыңдығын, демек эффективтік радиусын беретін, электролиттер теориясы үшін өте маңызды шама; ол ұзындық өлшемдерімен өлшенеді. Бұл шаманың мәні температураға, еріткіштің диэлектрлік тұрақтысына, иондардың зарядтары мен мөлшерлеріне тәуелді және иондардың термодинамикалық қасиеттерімен тығыз байланысты. Иондардың санын (n _i ) олардың концентрациясына (С) айналдырып [C=(n _i /N _A ) ∙1000 моль/л], (34) - теңдеуді былай жазайық:

$\frac{1}{\chi = \sqrt{(DkT \bullet 1000) /(4\pi e^{2}N_{A\ \sum z_{i}^{2}} \bullet C) }}$ $\frac{1}{\chi = \sqrt{(DkT \bullet 1000) /(4\pi e^{2}N_{A\ \sum z_{i}^{2}} \bullet C) }}$ (35)

Енді концентрациядан (35) - теңдеу бойынша иондық күшке (I) көшсек:

$\frac{1}{\chi = \sqrt{(DkT \bullet 1000) /(8\pi e^{2}N_{A\ }I) }}$ $\frac{1}{\chi = \sqrt{(DkT \bullet 1000) /(8\pi e^{2}N_{A\ }I) }}$ (36)

Теңдеудегі тұрақты шамалардың мәндерін қойсақ: (37)

$\frac{1}{\chi = \sqrt{\begin{array}{r} (1, 3805 \bullet 10^{- 16}10^{3}DT) /\lbrack 8 \bullet 3, 1416\left( 4, 8025 \bullet 10^{- 10}) ^{2} \times 6, 023 \bullet 10^{23} \bullet I \right\rbrack = \\ = 1, 9885 \bullet 10^{- 10}\sqrt{\frac{DT}{I}\ \ } \end{array}}}$

... жалғасы

Электролиз. Электрхимиялық өнеркәсіптердің даму және толық жетілдіру жолдары

Электролиз

Гальваникалық элемент

Электролит ерітінділердегі ионды ассоциация

Электрохимия жаңа дамып жатқан ғылым

Ерітіндінің концентрациясы еріген зат шамасының ерітінді шамасына қатынасы

ЭЛЕКТРОМЕТАЛЛУРГИЯЛЫҚ ҮРДІСТЕР ТЕОРИЯСЫ

Электр доғалық пісіру

Түсті металдарды және темірді өндірістік айнымалы токпен поляризациялау арқылы олардың бейорганикалық қосылыстарын синтездеу

Темір-аммоний ашудасын алудың электрохимиялық технологиясының негіздерін жасау

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс