Уақыт қатары (динамикалық қатарлар): талдау әдістері мен болжам жасау


9-Лекция. Уақыт қатарының талдауы мен болжамдары
(Динамикалық қатарлар)
Жоспары:
9. 1. Уақыт қатары туралы түсінік, уақыт қатарының түрлері.
9. 2. Уақыт қатарының көрсеткіштері.
9. 3. Уақыт қатарын талдау тәсілдері.
9. 4. Динамикалық қатарларда негізгі үрдістерді айқындау әдістері.
9. 5. Маусымдық ауытқуларды талдау.
9. 6. Тренд негізінде болжам жасау.
Мақсаты: Қоғамдық құбылыстар мен үрдістердің уақытқа байланысты өзгеруін зерттеу. Ол үшін, динамикалық қатарларды құру, оларды талдау арқылы жүзеге асырылады. Уақыт қатарының талдауы мен болжауы арқылы статистикалық көрсеткіштердің уақыт бойынша орналасқан мәндерін айқындау және де белгілі бір көрсеткіштің өсу қарқынын, көрсеткіш үлесінің өзгерісін сипаттау.
Тақырып бойынша негізгі ұғымдар: Уақыт қатары, динамикалық қатарлар, Қатар деңгейі, уақыт көрсеткіші, абсолютті шамалар, қатысты шамалар, орташа шамалар, мезеттік және интервалды қатар, Толық және орта қатарлар, абсолютті өсім, өсу қарқыны, өсім қарқыны, өсім қарқынының 1 пайыздық абсолютті мәні, базалық және тізбекті әдіс, өсу коэффициенті, даму үрдісі немесе тренд, парабола теңдеуі, маусымдық ауытқу, маусымдық индекс, экстраполяция, интерполяция, сенімділік интервалы.
Динамикалық қатарлар туралы түсінік
Статистиканың негізгі міндеттерінің бірі - қоғамдық қүбылыстар мен үдерістердің уақытқа байланысты өзгеруін зерттеу. Бұл міндет динамикалық қатарларды құру, оларды талдау арқылы жүзеге асырылады.
Динамикалық қатар деп статистикалық көрсеткіштердің уақыт бойынша орналасқан мәндерін айтады. Динамикалық қатарлар екі элементтен тұрады:
- қатар деңгейі
- уақыт көрсеткіші
Құбылыстың шамасын, мөлшерін сипаттайтын көрсеткіштің белгілі бір уақыттағы сандық мәнін қатардың деңгейі дейді. Уақыт көрсеткіші арқылы күн, ай, тоқсан, жыл сияқты уақыт бірліктері анықталады. Динамикалық қатарларды кесте түрінде былай көрсетуге болады:
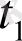
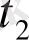
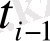
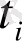
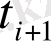
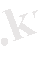
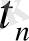
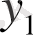
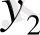
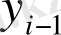
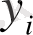
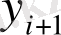
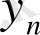
мұндағы,
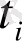 - уақыт көрсеткіші;
- уақыт көрсеткіші;
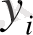 -
қатар деңгейі.
-
қатар деңгейі.
Динамикалық қатарлардың түрін мынадай белгілер бойынша анықтайды:
1. Қатар деңгейінің қандай шама арқылы өрнектелгеніне байланысты динамикалық қатарларды былай жіктейді:
- абсолютті шамалардың динамикалық қатарлары;
- қатысты шамалардың динамикалық қатарлары;
- орташа шамалардың динамикалық қатарлары.
Осы аталған қатарлардың ішінде абсолютті шамалардың динамикалық қатарлары құбылыстардың дамуын мейілінше толық сипаттайды. Мысалы, жалпы шығарылған өнімнің, бөлшек тауар айналымының динамикасын абсолютті шамалар арқылы өрнектейді. 9. 2-кестеде ҚР жалпы ұлттық табысының динамикасы көрсетілген.
9. 2-кесте ҚР жалпы ұлттық табысы
Қатысты шамалардың динамикалық қатарлары арқылы белгілі бір көрсеткіштің өсу қарқынын, көрсеткіш үлесінің өзгерісін, құрылымдық өзгерістерді сипаттауға болады. Мысалы, жан басына шаққандағы жалпы шығарылған өнім динамикасын, тауар айналымы құрылымындағы динамикалық өзгерістерді талдау үшін қатысты шамалардың динамикалық қатарлары қарастырылады. Төменде келтірілген 9. 3-кестеде ҚР жалпы ішкі өнімінің құрылымы ақырғы пайдалану әдісі бойынша есептелген.
9. 3-кесте ҚР жалпы ішкі өнімінің құрылымы, %
61, 1
30, 1
8, 8
55, 9
33, 4
10, 7
56, 1
37, 2
6, 7
59, 0
32, 8
8, 2
Орташа шамалардың динамикалық қатарлары құбылыс деңгейінің өзгерісін көрсету үшін қолданылады. Мұндай катарлардың мысалы ретінде халықтың жылдық орташа санының, экономика салаларындағы орташа жалақының динамикасын келтіруге болады (9. 4-кесте) .
9. 4-кесте Қазақстандағы орташа айлық атаулы жалақы динамикасы
2. Уақыт көрсеткіші бойынша динамикалық қатарлар екіге бөлінеді:
- мезеттік (мезгілдік)
- интервалды
Мезеттік қатарда қатар деңгейі құбылысты белгілі бір уақыт мезетіне (мысалы, айдың, тоқсанның, жылдың басындағы мәліметтер) байланысты сипаттайды. Төменде берілген Қазақстан халқының саны туралы мәліметтер мезеттік динамикалық қатардың мысалы болады.
9. 5-кесте Қазақстан Республикасы халқының саны
(мың адам)
Интервалды динамикальщ қатарда қатар деңгейі құбылысты белгілі бір уақыт аралығына (айлар, жылдар) байланысты көрсетеді (9. 6-кесте) .
9. 6-кесте Қазақстан Республикасынын жалпы ішкі өнімінің динамикасы
3. Даталар немесе интервалдар аралығына байланысты динамикалық қатарлар толық және орта болып бөлінеді. Толық динамикалық қатарларда уақыт мезеті немесе уақыт аралығы бірдей интервалмен беріледі (9. 7-кесте) .
9. 7-кесте Қазақстандағы экономикалық тұрғыдан белсенді халық динамикасы
Ал орта қатарларда бірдей интервал сақталмайды (9. 8-кесте) .
ҚР жалпы ішкі өнімінің нақты көлем индексі
7. 8-кесте ҚР жалпы ішкі өнімінің нақты көлем индексі
Динамикалық қатарлар мынадай талаптарға сай құрылуы қажет:
- дамуды кезеңдерге бөлу, яғни зерттелетін құбылысты уақытбойынша біртекті кезеңдерге бөлу. Мұндай бөлу әр кезеңкөрсеткішінің даму заңдылығын айқындауға мүмкіндікбереді.
- қатар деңгейлерінің салыстырмалы болуын қамтамасыз ету. Бұл талап бойынша қатар деңгейін анықтайтын көрсеткіштердіесептеу үшін бірдей әдіс, бірдей өлшем бірліктері, бірдейаумақтық шекаралар қолдануы тиіс. Сол сияқты әр деңгейдегібақылау объектілері де бірдей болуы қажет.
- қатар деңгейлерінің хронологиялық тәртіппен жүйелі түрдеанықтау, яғни уақыт интервалының шамасы зерттелетінқұбылыстың даму қарқындылығына сай анықталуы керек.
Статистикада динамикалық қатарларды мынадай міндеттерді шешу үшін қолданады.
- құбылыстың әр түрлі уақыттағы деңгейін сипаттайтын көрсеткіштерді анықтау;
- құбылыстың уақытқа байланысты өзгеру қарқындылығын сипаттайтын көрсеткіштерді анықтау;
- құбылыстың даму үрдісін айқындау;
- құбылыстың кезеңдік, маусымдық ауытқуларын зерттеу;
- құбылыс дамуына болжам жасау.
Осы міндеттерді шешу үшін алдымен динамикалық қатардың көрсеткіштер жүйесі анықталады.
Динамикалық қатар көрсеткіштері
Құбылыстардың динамикасын зерттеп, талдау үшін динамикалық қатарларлардың мынадай негізгі 4 көрсеткішін есептейді:
- абсолютті өсім
- өсу қарқыны
- өсім қарқыны
- өсім қарқынының 1%-ның абсолютті мэні
Бұл көрсеткіштерді есептеу динамикалық қатар деңгейлерін бір-бірімен салыстыруға негізделген. Жоғарыда аталған динамика көрсеткіштерінің алғашқы үшеуін базалық және тізбекті әдіспен анықгайды. Салыстыру негізі базалық әдісті қолданғанда тұрақты, ал тізбекті әдісте өзгермелі болады (9. 1-сурет) .
Базалык тәсіл
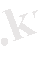
Тізбекті тәсіл
9. 1-сурет. Динамикалық қатар көрсеткіштерін базалық және тізбекті әдіспен есептеу үлгісі
Абсолютті өсім белгілі бір уақыт аралығында қатар деңгейлерінің қанша бірлікке өскенін немесе кемігенін көрсетеді. Бұл көрсеткішті базалық әдіс бойынша былай есептейді:
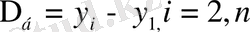 (9. 1)
(9. 1)
мұндағы,
 б
- базалық абсолютті өсім;
б
- базалық абсолютті өсім;
y і - көрсеткіштің ағымдағы мерзімдегі мәні;
у 1 - көрсеткіштің базалық мерзімдегі мәні.
Базалық әдіспен есептелген абсолютті өсім қарастырып отырған деңгейдің базалық (бастапқы) деңгеймен салыстырғанда қалай өзгергенін көрсетеді.
Тізбекті әдіспен абсолютті өсімді мына формуламен анықтайды:
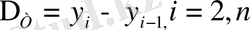 (9. 2)
(9. 2)
мұндағы,
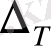 - тізбекті абсолютті өсім;
- тізбекті абсолютті өсім;
y
 -
ағымдағы мерзім алдындағы мерзімдегі көрсеткіштің деңгейі.
-
ағымдағы мерзім алдындағы мерзімдегі көрсеткіштің деңгейі.
Базалық және тізбекті әдіспен есептелген абсолютті өсімдердің арасында мынадай байланыс болады:
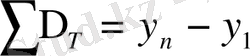 , (9. 3)
, (9. 3)
яғни, тізбекті абсолютті өсімдердің қосындысы қатардың соңғы деңгейінің базалық абсолютті өсіміне тең болады. Абсолютті өсім таңбасы оң да, теріс те болуы мүмкін.
Өсу қарқыны қатар деңгейлерінің өзгеру қарқындылығын сипаттайды. Бұл көрсеткіш салыстырылатын деңгейдің базалық деңгейден неше есе артық екенін немесе салыстырылатын деңгей базалық деңгейдің неше пайызын құрайтынын көрсетеді. Өсу қарқыны коэффициент немесе пайызбен өлшенеді. Деңгейлерді салыстыру нәтижесін коэффициент түрінде анықтағанда өзгеру қарқындылығын өсу коэффициенті дейді.
Өсу қарқынын (өсу коэффициентін) абсолютті өсім сияқты базалық және тізбекті әдіспен есептейді. Базалық өсу коэффициентін анықтау үшін ағымдағы мерзімдегі деңгейді базалык мерзім деңгейіне бөледі:
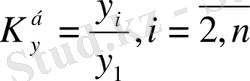 ; (9. 4)
; (9. 4)
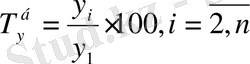 ; (9. 5)
; (9. 5)
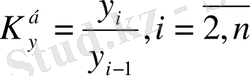 ; (9. 6)
; (9. 6)
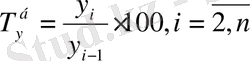 ; (9. 7)
; (9. 7)
Базалық және тізбекті әдіспен есептелген өсу қарқындарының арасындағы өзара байланысты мынадай формуламен көрсетуге болады:
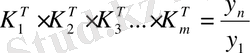 ; (9. 8)
; (9. 8)
яғни, тізбекті әдіспен анықталған өсу коэффициенттерінің көбейтіндісі сол мерзімдегі базалық әдіспен есептелген өсу коэффициентіне тең.
Өсу қарқынының мәні әрқашан оң сан болады. Егер өсу қарқыны 100%-ге тең болса, бұл деңгей мәні өзгермегенін көрсетеді. Егер өсу қарқыны 100 пайыздан артық болса, ол қатар деңгейінің жоғарлағанын, ал 100 пайыздан кем болса, қатар деңгейінің төмендегенін көрсетеді.
Өсім қарқыны деп абсолютті өсімнің базалық деңгейге немесе алдыңғы мерзім деңгейіне қатынасын айтады. Бұл көрсеткіш салыстырылатын деңгейдің базалық деңгеймен салыстырғанда неше пайызға өскенін немесе кемігенін білдіреді. Егер өсу қарқыны әрқашан тек оң сан болса, өсім қарқыны оң, теріс, нөлге тең болуы мүмкін.
Базалық әдіспен өсім қарқынын былай анықтайды :
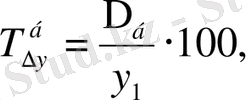 (9. 9)
(9. 9)
мұндағы, Т
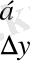 - базалық әдіспен есептелген өсім қарқыны;
- базалық әдіспен есептелген өсім қарқыны;
 б
- базалық абсолютті өсім;
б
- базалық абсолютті өсім;
Ал тізбекті әдісті қолданғанда бұл көрсеткішті мына формуламен есептейді:
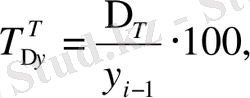 (9. 10)
(9. 10)
мұндағы,
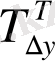 - тізбекті әдіспен есептелген өсім қарқыны;
- тізбекті әдіспен есептелген өсім қарқыны;
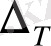 - тізбекті абсолютті өсім;
- тізбекті абсолютті өсім;
Өсім қарқынын есептейтін формулаларды түрлендіру арқылы өсу қарқыны мен өсім қарқынының арасындағы байланысты көрсететін мынадай формуланы қорытып шығаруға болады:
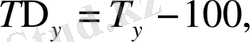 (9. 11)
(9. 11)
яғни, өсім қарқыны өсу қарқынынан 100 пайызды шегергеннен кейінгіқалдыққа тең.
Өсім қарқынының 1 пайызының абсолютті мәні тізбекті тәсілмен есептелген абсолютті өсімнің өсім қарқынына қатынасын көрсетеді.
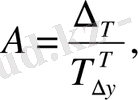 (9. 12)
(9. 12)
мұндағы, А - өсім қарқынының 1 пайызының абсолютті мәні.
Өсім қарқынының 1 пайызының абсолютті мәнін өсім қарқынын бағалау үшін қолданады. Бұл көрсеткіш өсім қарқынының 1 пайызына қандай абсолютті мән сәйкес келетінін білдіреді.
Математикалық түрлендірулер жасау арқылы бұл формуланы да өзгертіп, мынадай түрге келтіруге болады:
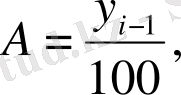 (9. 13)
(9. 13)
Динамикалық қатардың негізгі көрсеткіштерін есептеу формулалары қолдануға тиімді болу үшін жинақталып, 9. 9-кестеде көрсетілген.
9. 9-кесте Динамикалық қатардын негізгі корсеткіштерін есептеу формулалары
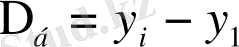
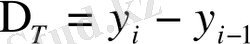
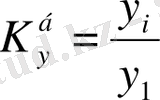
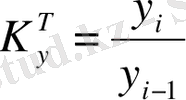
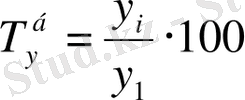
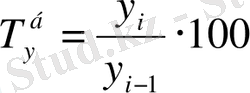
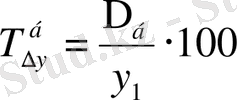
немесе
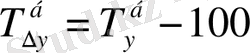
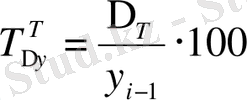
немесе
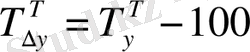
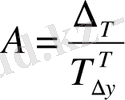 немесе
немесе
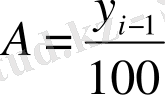
Динамикалық қатарларда орта көрсеткіштерді есептеу .
Динамикалық қатар сипаттамасы ретінде қатардың орташа деңгейі У орт алуға болады. Ол орташа хронологиялық деп аталады. Интервалдық қатарда тұрақты периодты абсолюттік шамалардың орташа деңгейі арифметикалық орта шама болады. Мысалы,
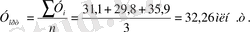 (9. 14)
(9. 14)
Әр түрлі динамикалық қатарлар үшін орта мәні әр түрлі әдіспен есептеледі. Моменттік қатар үшін аз ғана өзгешелік бар. Бірдей моменттік аралыққа бөлінген п деңгейлі қатар үшін мына формула қолданылады:
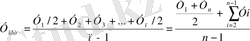 (9. 15)
(9. 15)
Бұл орта шама статистикада моменттік қатарлар үшін хронологиялық орта мән болып есептелінеді.
Егер момент араларындағы уақыт бірлігі әр түрлі болғанда, оны әр момент үшін орташа арифметикалық формуламен есептеуге болады.
 (9. 16)
(9. 16)
Мысалы, 2005 ж. қоймадағы тауар қалдықтарының мәліметтері келесі кестеде көрсетілген
Кесте 9. 10. Қоймадағы тауарлық қалдықтар туралы мәліметтер
Онда 2005ж. орташа 1 айдағы тауарлық қалдық мынаған тең болды:
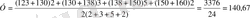
Қатардың орташа абсолюттік өсімшесі жеке тізбектелген өсімше тәріздес арифметикалық орта мән формуласымен есептеледі.
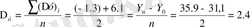
Динамикалық қатарларда орташа өсу қарқынын есептеуге ерекше мән беріледі. Көп жағдайда орташа өсу қарқыны алдыңғысына қатысты әр периодта тізбектелген өсу қарқынынан тұратын орташа геометриялық түрінде есептелінеді

немесе
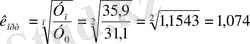
Сонымен қатар, өсу деңгейінің орта коэффициентін есептегенде шеткі деңгейлерге ғана мән бермей, кейде деңгейдің барлық сомасына да мән берген дұрыс. Мысалы, инвестиция енгізу, тұрғын үй аудандарын іске қосу, автомобильдік жолдар құрылысын жасау сияқты мәселеге келгенде, бұл жерде тек шеткі деңгейді ғана емес, анализ жасалған периодтың сомасы шығатын орташа өсу қарқынын анықтаған жөн. Бұдан орта мән параболалық деп аталады және төмендегідей формуламен есептелінеді:
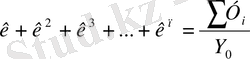 (9. 17)
(9. 17)
Мысалы, берілген 17 кесте бойынша берілген 2005-2010ж. іске қосылған тұрғын үй аудандарының орташа өсу коэффициентін анықтау керек.
Кесте 9. 11 - Тұрғын үй аудандары көлемі
Алдымен орташа өсу қарқынын анықтаймыз
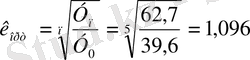
яғни жыл сайын тұрғын үйлерді іске қосу 9, 6% өседі. Жылдық өсу қарқынын есептеу үшін іске қосылған тұрғын үйлердің бүкіл периодтағы сомалар қосындысын есептеп алып формулаға қоямыз.

п=5 болғанда 6, 66-ге жақын мәнді аламыз және ол к=1, 095 немесе Т=109, 5% шамаларына сәйкес келеді. Бұл тұрғын үйдің жылдық іске қосылуы орташа мәнмен 9, 5% өсіп отырады дегенді білдіреді.
Маусымдық ауытқуларды талдау.
Көптеген экономикалық кұбылыстардың тоқсандық немесе айлық мәліметтерін қарастырғанда, олардың дамуында жыл мезгілдеріне байланысты болатын ауыткулар байқалады. Мұндай ауытқуларды маусымдың ауыткулар немесе маусымдық толқындар дейді. Мысалы, жаз айларында электр энергиясын өндір кемиді, жазғы киімдерге сұраныс көбейеді, жеміс-жидектер көп сатылады, т. с. с. Маусымдық ауытқулардың ауыл шаруашылығы, құрылыс, көлік, туризм, т. б. экономика салаларындағы атқаратын рөлі жоғары. Экономика салалары бір-бірімен байланысты болғандықтан, маусымдық ауытқулар жалпы экономикалық дамуға өз ықпалын тигізеді. Жұмыс күші, материалдық ресурстар, өндіріс қуаты біркелкі , маусымдық ауытқулар экономикалық әрекет нәтижесіне кері әсер етеді. Маусымдық ауытқулар климаттық жағдайларға, әр түрлі экономикалық факторларға байланысты болады.
Әдетте маусымдық ауытқулар жыл сайын қайталаньш отырады. Маусымдық ауытқуларды айқындау және өлшеу үшін мынадай әдістер қолданылады:
- маусымдық индекстер;
- гармониялық талдау
Маусымдық индекстер деп жылдың әр айының нақты деңгейінің орташа деңгейге қатынасын айтады:
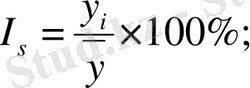
Маусымдық ауытқуларды бірнеше жылдың айлық немесе тоқсандық мәліметтері бойынша зерттейді. Бірнеше жылдың мәліметтері маусымдық ауытқуларға бір жыл ішінде болған кездейсоқ факторлар әсер етпеу үшін және тұрақты маусымдық толқынды айқындау үшін қажет. Әдетте зерттелетін құбылыстың даму заңдылығын айқындау үшін үш жылдың мәліметтері алынады. Мұндай жағдайда маусымдық индексті мына формуламен есептейді:
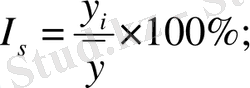
Маусымдық индекс:
Үш жыл деңгейлерінің арифметикалық орташа арқылы анықтайды:
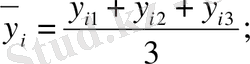
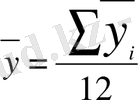
Жалпы орташа деңгей:
Тренд негізінде болжам жасау.
Динамикалық қатарларды талдау нәтижесінде алынған мәліметтер құбылыстың болашақта қалай дамитынына болжам жасауға мүмкіндік береді. Статистикалық болжам өткен мерзімде байқалған даму заңдылығы болжам жасалатын мерзімде де сақталады деген жорамалға негізделеді. Мұндай болжам экстраполяция деп аталады. Болжам дәлдігі болжамдау мерзіміне байланысты болады. Болжам жасалатын мерзім неғұрлым қысқа соғұрлым жоғары болады, себебі құбылыстың даму шартгары қысқа мерзімде айтарлықтай өзгеріп үлгермейді. Сондықтан болжам жасалатын мерзімді тренд есептелетін база ұзақтығының үштен бір бөлігінен асырмаған дұрыс. Экстраполяция әдісі арқылы болжамның екі түрін жасауға болады:
- нүктелі;
- интервалды.
Нүктелік болжам көрсеткіш деңгейінің болжам жасалатын мерзімдегі нақты сандық мәнін анықтауды білдіреді, ал интервалды болжам деңгейдің сандық мәндерінің диапазонын, интервалын анықтауды көздейді. Болжам жасау негізі ретінде қандай бастапқы мәліметтер алынғанына байланысты экстраполяцияның мынадай әдістері қолданылады:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz