Коши интегралдық формуласы және интегралдарды есептеу мысалдары


Кошидің интегралдық формуласы
Егер
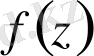 функциясы
функциясы
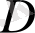 облысында аналитикалық, сонымен қатар С тұйық контурымен және сол контурда шектелген болса, онда төмендегі Коши интегралдық формуласы дұрыс болады
облысында аналитикалық, сонымен қатар С тұйық контурымен және сол контурда шектелген болса, онда төмендегі Коши интегралдық формуласы дұрыс болады
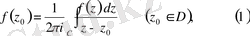
С контуры бар жерде Dобласы әрқашан сол жақта қалады.
Кошидің интегралдық формуласы арқылы кейбір интегралдарды есептеуге болады.
Мысал 1. Интегралды есептеңіз
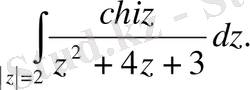
Шешуі.
Ішкі ортада
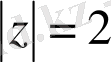 түбірдің бөлімі нүктесінде нөлге айналады. (1) формуланы қолдану үшін интегралды келесі түрде жазып аламыз:
түбірдің бөлімі нүктесінде нөлге айналады. (1) формуланы қолдану үшін интегралды келесі түрде жазып аламыз:
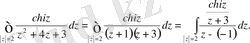
Мұндағы
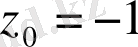 және
және
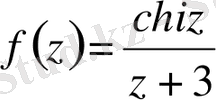 функциясы
функциясы
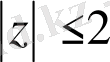 ортада аналитикалық болып саналады. Сондықтан
ортада аналитикалық болып саналады. Сондықтан
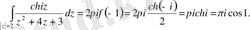
Мысал 2.
Коши интегралдық формуласын қолданып,
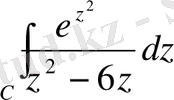 интегралды есептеңіз, егер
интегралды есептеңіз, егер
1)
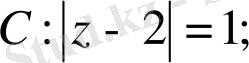 2)
2)
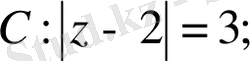 3)
3)
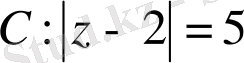 тең болса.
тең болса.
Шешуі.
1) Тұйық облыста
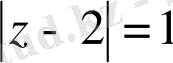 шектелген, интеграл астындағы функция аналитикалық, сондықтан Коши теоремасы өз күшінде
шектелген, интеграл астындағы функция аналитикалық, сондықтан Коши теоремасы өз күшінде
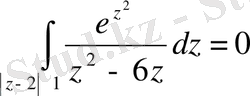
2) Облыс ішінде
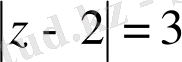 шектелген,
шектелген,
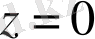 бір нүктесі табылады және бөлшектің бөлімі нөлге айналады. Интегралды келесі түрде жазып аламыз
бір нүктесі табылады және бөлшектің бөлімі нөлге айналады. Интегралды келесі түрде жазып аламыз
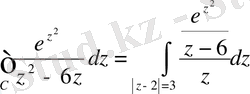 .
.
Бұл облыста
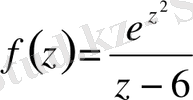 функциясы аналитикалық. Коши
функциясы аналитикалық. Коши
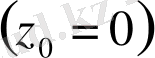 интегралдық формуласын қолданып, мынаны аламыз
интегралдық формуласын қолданып, мынаны аламыз
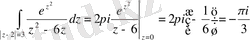 .
.
3)
 шектелген облыста екі нүкте бар олар
шектелген облыста екі нүкте бар олар
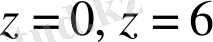 , осы нүктелерде интеграл астындағы өрнектің мәні нөлге тең болады. (1) формуланы қолдануға болмайды. Бқл жағдайда интегралды табу үшін былай жасауға болады.
, осы нүктелерде интеграл астындағы өрнектің мәні нөлге тең болады. (1) формуланы қолдануға болмайды. Бқл жағдайда интегралды табу үшін былай жасауға болады.
Бірінші әдіс.
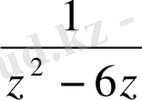 бөлшекті қарапайым түрге келтіреміз. Сонда
бөлшекті қарапайым түрге келтіреміз. Сонда
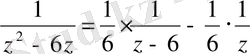 .
.
Интегралға қоя отырып, алатынымыз
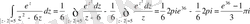 .
.
Екінші әдіс.
Центрі
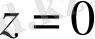 және
және
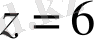 нүтелерінде жататын
нүтелерінде жататын
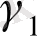 және
және
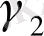 шеңберлерін сызып алып, олардың радиустары өте кіші, бір -бірімен қиылыспайтын және
шеңберлерін сызып алып, олардың радиустары өте кіші, бір -бірімен қиылыспайтын және
 шеңберде толығымен жататындай етіп тұрғызуымыз қажет (6 - сурет) .
шеңберде толығымен жататындай етіп тұрғызуымыз қажет (6 - сурет) .
Үш өлшемді облыста
 шеңберімен шектелген
шеңберімен шектелген
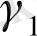 және
және
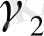 интеграл астындағы функция барлық жерде аналитикалық болып саналады. Коши теоремасы бойынша көпөлшемді облыстар үшін
интеграл астындағы функция барлық жерде аналитикалық болып саналады. Коши теоремасы бойынша көпөлшемді облыстар үшін
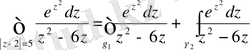
Оң жақтағы әрбір интеграл үшін (1) Кошидің интегралдық формуласын қолдана аламыз. Нәтижесінде

аламыз.
Кошидің интегралдық формуласын қолданып келесі интегралдардың барлығын есептеңіз (барлық шеңбердің бағытын сағат тіліне қарама - қарсы деп алыңыз) :
175.
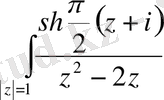 176.
176.
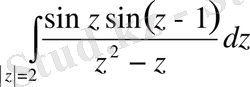
Егер
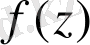 функциясы
функциясы
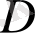 облысында және оның
облысында және оның
 шекарасында аналитикалық болса, онда кез келген натурал
шекарасында аналитикалық болса, онда кез келген натурал
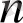 үшін мына формуланы қолдануға болады
үшін мына формуланы қолдануға болады
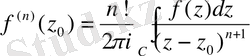 , (2)
, (2)
мұндағы
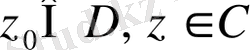 . (2) формуланы кейбір интегралдарды есептеу үшін қолдануға болады.
. (2) формуланы кейбір интегралдарды есептеу үшін қолдануға болады.
Мысал 3.
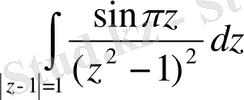 интегралын есепте.
интегралын есепте.
Шешуі.
Интегралдағы астындағы
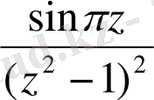 функциясы
функциясы
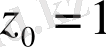 нүктесінен басқа, барлық
нүктесінен басқа, барлық
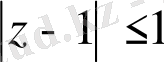 облысында аналитикалық болып табылады.
облысында аналитикалық болып табылады.
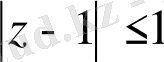 шеңберінде аналитикалық болатын интеграл белгісінің астындағы
шеңберінде аналитикалық болатын интеграл белгісінің астындағы
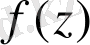 функциясын таңдап аламыз. Ол үшін интеграл астындағы функцияны мына түрде жазып аламыз
функциясын таңдап аламыз. Ол үшін интеграл астындағы функцияны мына түрде жазып аламыз
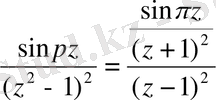 ,
,
және
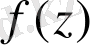 ретінде
ретінде
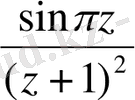 аламыз. (2) формула бойынша
аламыз. (2) формула бойынша
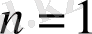 деп болжап, мынаған келеміз
деп болжап, мынаған келеміз
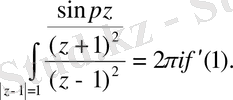
Туындыларды тапсақ
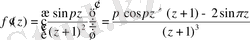 .
.
Бұдан
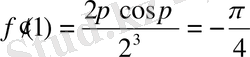 .
.
Демек,
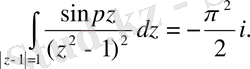
Мысал 4.
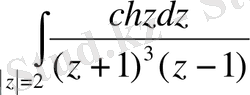 интегралын есепте.
интегралын есепте.
Шешуі.
Бірінші тәсіл.
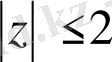 шеңберінің ішінде жатқан интеграл астындағы бөлінгіш
шеңберінің ішінде жатқан интеграл астындағы бөлінгіш
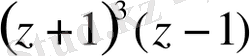 функциясы мына екі
функциясы мына екі
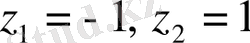 нүктесінде нөлге айналады. Функцияны қарапайым бөлшектерге жіктесек
нүктесінде нөлге айналады. Функцияны қарапайым бөлшектерге жіктесек
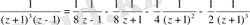 .
.
Интегралдың сызықтылығын пайдаланып, мынаған келеміз
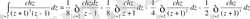 .
.
Бірінші екі интегралға (1) Коши интеграл формуласын қолданамыз:
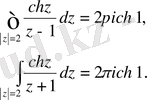
Үшінші және төртінші интегралды (2) формуланың көмегімен есептейміз:
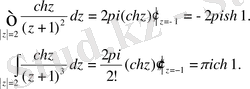
Соңында мынаған келеміз
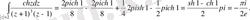
Екінші тәсіл.
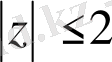 шеңберінде толығымен жататын және шеңберлер өзара қиылыспайтындай радиусы кіші
шеңберінде толығымен жататын және шеңберлер өзара қиылыспайтындай радиусы кіші
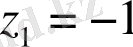 және
және
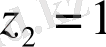 нүктелері центр болатын
нүктелері центр болатын
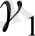 және
және
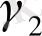 шеңберлерін саламыз.
шеңберлерін саламыз.
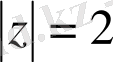 шеңберінде шектелген, үшөлшемді, интеграл астындағы
шеңберінде шектелген, үшөлшемді, интеграл астындағы
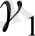 және
және
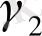 функциялар барлық жерде аналитикалық болады. Коши теоремасы бойынша көпөлшемді облыстар үшін
функциялар барлық жерде аналитикалық болады. Коши теоремасы бойынша көпөлшемді облыстар үшін
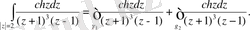 (3)
(3)
(3) -тің бірінші интегралының оң жақ бөлігіне (2) формуланы қолданып, интеграл астындағы функцияны алдын - ала мына түрде ұсынамыз
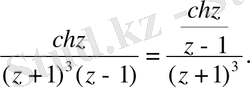
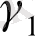 -дің ішкі облысында
-дің ішкі облысында
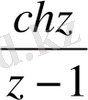 функциясы аналитикалық болып табылады, сондықтан (2) формула бойынша
функциясы аналитикалық болып табылады, сондықтан (2) формула бойынша
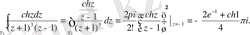
(3) - тің екінші интегралының оң жақ бөлігіне Кошидің (1) интегралдық формуласын қолданамыз
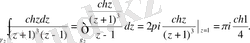
Ең соңында мынаған келеміз
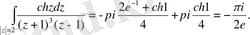
Келесі интегралдарды есептеңіз:
177.
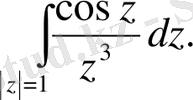 178.
178.
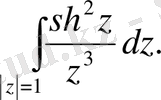
179.
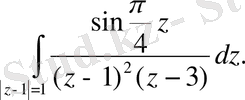 180.
180.
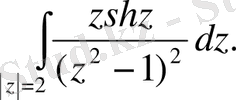
181.
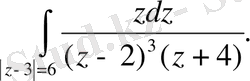 182.
182.
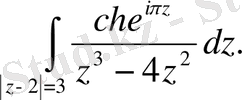
183.
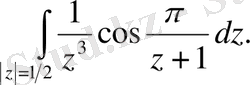 184.
184.
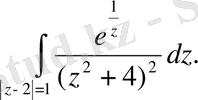
185.
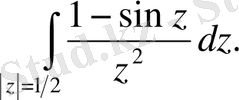 186.
186.
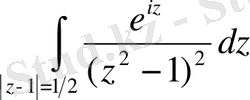
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz