Мектептегі тригонометриялық теңдеулер мен теңсіздіктер және олардың жүйелерін оқыту әдістемесі


Қазақстан Республикасының Білім және ғылым министрлігі
Академик Е. А. Бөкетов атындағы Қарағанды мемлекеттік университеті
Математика және Ақпараттық технологиялар факультеті
Математика және информатика әдістемесін оқыту кафедрасы
«Мектептің үдерісінің ұйымдастырудың инновациялық технологиялары» пәні бойынша
КУРСТЫҚ ЖҰМЫС
Тақырыбы: «Тригонометриялық теңдеулер мен теңсіздіктер, олардың жүйелерін оқыту әдістемесі»
Мамандық: 5B010900 - «Математика»
Орындаған: М-301 тобының студенті
Рысқұл Б. С.
Тексерген: аға оқытушы
Шегирова Д. К.
Қарағанды 2018
Мазмұны
КІРІСПЕ
Қазақстан Республикасы білім және ғылым министрлігінің нұсқалығына сәйкес, егер біз Қазақстан экономикасын, мәдениетін дамытып, жоғары дамыған елдердің қатарына жеткіземіз десек, онда бірінші орында білімді дамытуға тиіспіз. Ол үшін Қазақстанды болашақта өрге жетелейтін білікті мамандар даярлап, Отанына адал қызмет ететін азамат тәрбиелеп шығаруымыз керек. Қазіргі кезде осы мақсаттарды жүзеге асыру үшін жалпы білім беретін орындарға қойылған талаптар қатаңдалып, күннен күнге өсуде. Соның ішінде мектеп курсындағы гуманитарлық пәндер арасында математиканы оқыту үлкен іскерлікті қажет етеді. Мектепте математиканы оқыту - онымен тығыз байланыста жүретін пәндерді меңгеруге, күнделікті тұрмысқа қажетті біліктілік пен дағдыны қалыптастыруға және математиканы тереңдетіп оқытуға тиіс. Математиканы тереңдетіп оқыту - оқушының математикаға тұрақты қызығушылығын тудырып, олардың математикалық қабілеттілігін дер кезінде анықтап, дамуына ықпал етеді де жоғарғы оқу орнына түсуге дайындық мәселелерін шешеді. Оқушылардың математикалық даму әрежесі олардың есеп шығару қабілеттілігінен көрінеді. Кез - келген қиын есепті шығару оқушылардың үлкен еңбекті талап етеді. Мұғалімнің міндеті баланың бойындағы қасиеттерді ояту болып табылады.
Ол үшін мұғалімнің үздіксіз ізденуін, әдістемелік - теориялық білімін жүйелі көтеріп отыруын, терең толғауын, оқушылардың психологиясын зерттеп, тақырып ерекшелігін жете талдай білуін қажет етеді. Әсіресе бұл талаптар жоғары сыныптарда күшейе түседі. Соның ішінде 10 - сыныпта оқытылатын тригонометрия тақырыбының өзі үлкен бір тарау болып келеді. Тригонометриялық функциялар негізгі үш параграфтан тұрады. Соның ішінде біз тригонометриялық теңдеулер, теңсіздіктер және олардың жүйелерін шешу әдістерін қарастырамыз. Бұлардың ішіндегі тригонометриялық теңдеулер, теңсіздіктер тақырыбы өте күрделі. Оқушылар тригонометриялық теңдеулер мен теңсіздіктерді шешкенде үлкен қиындықтарға кездеседі. Сол себепті де мен өзімнің курстық жұмысымның тақырыбын Тригонометриялық теңдеуле теңсіздіктер және олардың жүйелерін шешу жолдары деген тақырыпқа арнадым. Курстық жұмысымды жазу барысында мынандай мақсат, міндеттер қойдым.
Мақсаты:
Жалпы тригонометриялық теңдеулердің, теңсіздіктердің түрлерін және олардың шешу жолдарын ашып көрсету.
Міндеті:
1. Тригонометриялық теңдеулердің, теңсіздіктердің шешу жолдарын көрсету. 2. Тригонометриялық теңдеулерді және теңсіздіктерді шешкенде ыңғайлы әрі оңай жолын таңдауға үйрету.
1 Тригонометриялық теңдеулер
1. 1 Қарапайым тригонометриялық теңдеулерді шешу
Анықтама . Құрамында белгісіз айнымалыға тәуелді тригонометриялық теңдеулер деп атайды.
Тригонометриялық теңдеулерді шешуді негізінен мынадай қарапайым тригонометриялық теңдеулерге келтіріп алып шешеді:
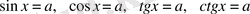 . Енді осы теңдеулерді шешу тәсілдерін қарастырайық.
. Енді осы теңдеулерді шешу тәсілдерін қарастырайық.
- теңдеуі. Егерболса, онда бұл теңдеудің екі шешімі бар:жәнеАлболғандықтан, бұл шешімдерді сәйкесжәненемесе оларды біріктіріп, түрінде жазуға болады. Мұндаболатынын ескерсек, онда берілген теңдеудің шешімін
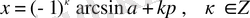 (1)
(1)
түрінде жазамыз. Егер
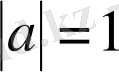 немесе
немесе
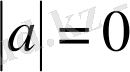 болса, онда (1) формуладан төмендегідей дербес жағдайлардағы формулаларды аламыз:
болса, онда (1) формуладан төмендегідей дербес жағдайлардағы формулаларды аламыз:
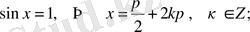
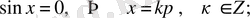 (2)
(2)
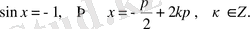
- теңдеуі. Оның шешімдері
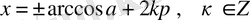 (3)
(3)
түрінде жазылады. Мұны 42-суретте көрсетілгендей етіп дәлелдеуге болады. Формуланың дербес жағдайлары (
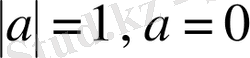 ) :
) :
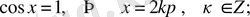 (4)
(4)
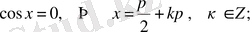
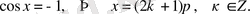
- теңдеуінің шешімдері
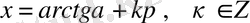
- теңдеуінің шешімдері
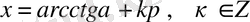
- мысал. теңдеуін шешу қажет.
Шешуі . Берілген теңдеуді 2-ге бөліп, оны
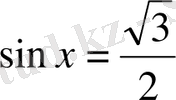 түрінде жазамыз. Онда (1) формула бойынша
түрінде жазамыз. Онда (1) формула бойынша
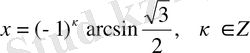 болады. Ал
болады. Ал
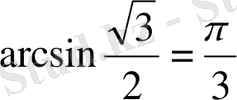
екенін ескерсек, онда берілген теңдеуінің шешімі
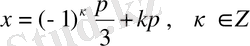 түрінде жазылады.
түрінде жазылады.
1. 2 Тригонометриялық теңдеулерді шешу әдістері
Тригонометриялық өрнектерден құралған теңдеулерді тригонометриялық теңдеулер деп атайды. Жалпы, тригонометриялық теңдеулерді түрлендірулер арқылы қарапайым тригонометриялық теңдеулерге келтіріп шешеді. Ал тригонометриялық теңдеулерді қарапайым теңдеулерге келтірудің жиі қолданылатын бірнеше әдісі бар. Енді осы әдістерге мысалдар келтіру арқылы тоқталып өтейік.

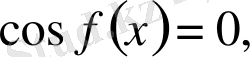 түріндегі теңдеулер. Мұнда
түріндегі теңдеулер. Мұнда
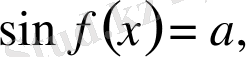
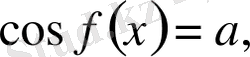
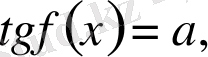
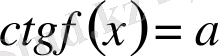 теңдеулер мен
теңдеулер мен
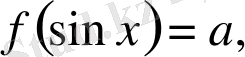
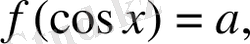
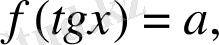
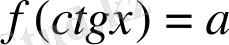 теңдеулерін шешу әдістерін қарастырамыз.
теңдеулерін шешу әдістерін қарастырамыз.
Мысал.
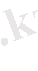
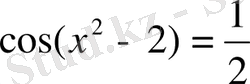 теңдеуінің нақты шешімдерін табу қажет.
теңдеуінің нақты шешімдерін табу қажет.
Шешуі: Жоғарыда айтылғандай, бұл теңдеудің шешуі
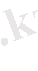
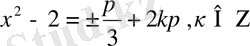
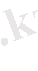 немесе
немесе
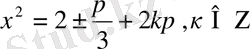 теңдеуін шешуге келіп тіреледі.
теңдеуін шешуге келіп тіреледі.
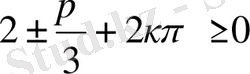 шарты
шарты
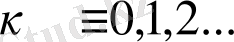 болғанда ғана орындалады.
болғанда ғана орындалады.
Онда берілген теңдеудің шешімдері
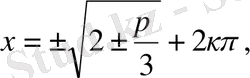
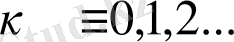 түрінде жазылады.
түрінде жазылады.
Жауабы:
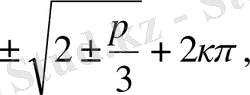
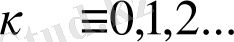 .
.
Біртекті теңдеулер.
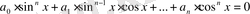 түріндегі теңдеулерді
түріндегі теңдеулерді
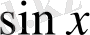 пен қатысты
пен қатысты
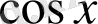 -ке
біртеті теңдеулер
деп атайды. Мұнда
-ке
біртеті теңдеулер
деп атайды. Мұнда
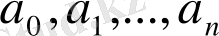 - берілген нақты сандар
- берілген нақты сандар
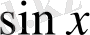 және
және
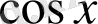 -тің әрбір қосылғыштағы пен дәрежелерінің қосындысы
-тің әрбір қосылғыштағы пен дәрежелерінің қосындысы
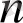 -ге тең. Бұл теңдеуді,
-ге тең. Бұл теңдеуді,
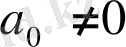 болған жағдайда
болған жағдайда
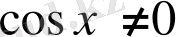 болатынын ескере отырып,
болатынын ескере отырып,
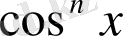 -ке бөлу арылы
-ке бөлу арылы
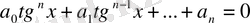 теңдеуіне келтіреміз. Ал
теңдеуіне келтіреміз. Ал
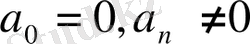 болған жағдайда бұл теңдеуді
болған жағдайда бұл теңдеуді
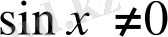 бөлу керек.
бөлу керек.
Мысал.
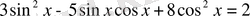 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі:
 қолдана отырып, берілген теңдеуді
қолдана отырып, берілген теңдеуді
 немесе
немесе
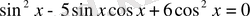 түріне келтіреміз. Енді бұл теңдеуді
түріне келтіреміз. Енді бұл теңдеуді
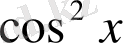 - ке бөлу арқылы (мұнда
- ке бөлу арқылы (мұнда
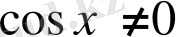 )
)
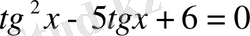 түрінде жазамыз. Осыдан
түрінде жазамыз. Осыдан
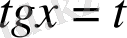 деп алсақ, онда
деп алсақ, онда
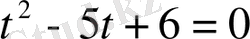 квадрат теңдеуі шығады. Оның түбірлері
квадрат теңдеуі шығады. Оның түбірлері
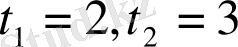 болғандықтан,
болғандықтан,
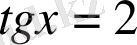 және
және
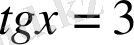 қарапайым тригометриялық теңдеулерін шешу керек:
қарапайым тригометриялық теңдеулерін шешу керек:
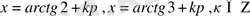 .
.
Қосымша бұрыш енгізу әдісі.
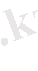
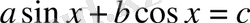 (7)
(7)
Түріндегі теңдеулерді шешудің ең тиімдң әдісі - ол қосымша бұрыш енгәу әдісі. Егер
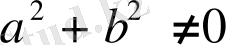 болса, онда (7) теңдеуді
болса, онда (7) теңдеуді
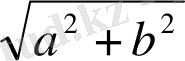 санына бөлеміз:
санына бөлеміз:
Мұнда
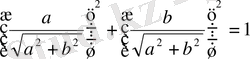 болғандықтан,
болғандықтан,
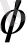 бұрышы табылып,
бұрышы табылып,
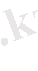
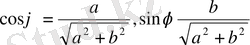 теңдіктері орындалады.
теңдіктері орындалады.
Онда берлен теңдеуді
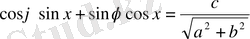
немесе
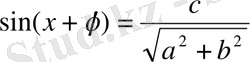 (8)
(8)
түрінде жазамыз. Егер
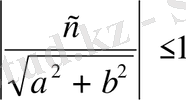 немесе
немесе
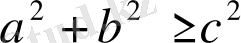 болса ғана, (8) теңдеудің шешімдері болады және ол
болса ғана, (8) теңдеудің шешімдері болады және ол
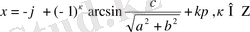 түрінде жазылады. Мұнда
түрінде жазылады. Мұнда
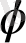 -дің
-дің
орнына
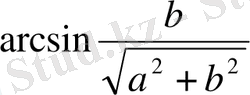 және
және
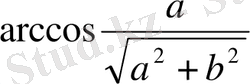 мәндерінің кез келгенін алуға болады және
мәндерінің кез келгенін алуға болады және
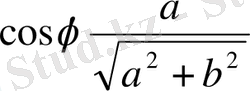 және
және
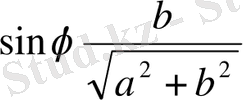 белгілеулрінің орнына
белгілеулрінің орнына
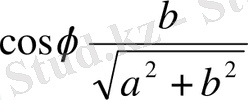 және
және
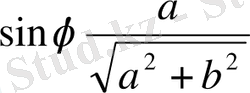 белгілеулерін де қолдануға болады.
белгілеулерін де қолдануға болады.
Белгісізді алмастыру әдісі
Егер берілген тригонометриялық теңдеуді түрлендірулер арқылы
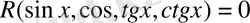 түріне келтірсек, мұнда R -рационал функция, онда
түріне келтірсек, мұнда R -рационал функция, онда
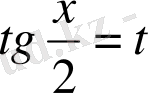 әмбебап алмастыруын қолданылады:
әмбебап алмастыруын қолданылады:
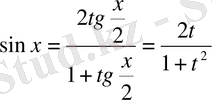
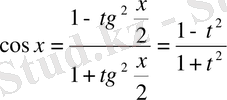
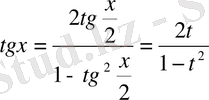
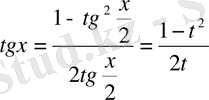
Мысал.
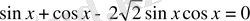 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі:
 деп алып, берілген теңдеуді
деп алып, берілген теңдеуді
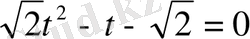 түріне келтіреміз. Оның түбірлері:
түріне келтіреміз. Оның түбірлері:
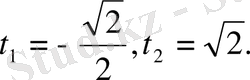 Онда
Онда
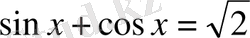 және
және
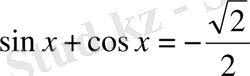 теңдеулерін шешу қажет. 3-пункте көрсетілген қосымша бұрыштар енгізу әдісімен соңғы теңдеулердің шешімдерін анытау қиын емес.
теңдеулерін шешу қажет. 3-пункте көрсетілген қосымша бұрыштар енгізу әдісімен соңғы теңдеулердің шешімдерін анытау қиын емес.
Жауабы:
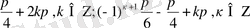
Көбейткіштерге жіктеу әдісі.
Мысал.
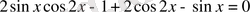 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі:
Теңдеуідің сол жақ бөлігін топтап, оны былай жызамыз:
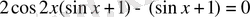 немесе
немесе
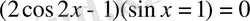 . Бұл теңдеу мынадай екі теңдеуге жіктеледі:
. Бұл теңдеу мынадай екі теңдеуге жіктеледі:
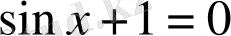 және
және
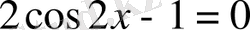
Жауабы:
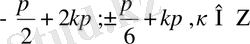
Теңдеудің оң жақ және сол жақ бөліктерін бағалау әдісі.
Алдын ала теңдеудің оң жақ және сол жақ бөліктерін бағалау арқылы оның түбірлері бар болатынын немесе жоқ болатыын анықтауға болады. Осыған мысал қарастырайық.
Мысал.
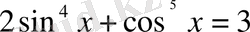 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі:
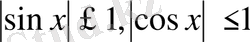 болғандықтан,
болғандықтан,
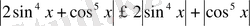 болса, онда
болса, онда
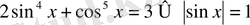 және
және
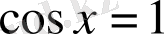 болған ғана теңдіу орындалады. Ал
болған ғана теңдіу орындалады. Ал
 болғандықтан,
болғандықтан,
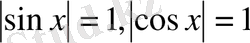 теңдіктері жүйесі орындалатындай
теңдіктері жүйесі орындалатындай
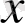 -тің мәнін табу мүмкін емес. Сондықтан берілген теңдеудің шешімі жоқ. Жауабы:
-тің мәнін табу мүмкін емес. Сондықтан берілген теңдеудің шешімі жоқ. Жауабы:

1. 3 Тригонометриялық теңдеулер жүйесін шешу
Біз мұнда теңдеулер жүйесін шешудің жалпы ережелеріне сүйене отырып, тригонометриялық теңдеулердің кейбір жиі кездесетін түрлеріне тоқталамыз.
1.
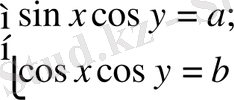
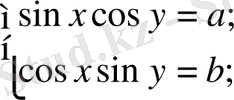
түріндегі жүйелер.
Бұл жүйеледі шешу үшін олардың бір теңдеуіне екіншісіне қосып, азайту арқылы.
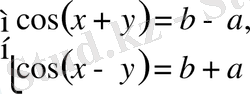 және
және
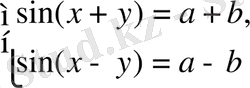 жүйелеріне келтіріп аламыз. Әрине, бұл жүйелердің нақты шешімдері бар болуы үшін
жүйелеріне келтіріп аламыз. Әрине, бұл жүйелердің нақты шешімдері бар болуы үшін
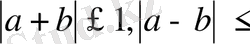 1 теңсіздіктерінің орындалуы қажетті және жеткілікті. Енді мысалдар қарастырайық.
1 теңсіздіктерінің орындалуы қажетті және жеткілікті. Енді мысалдар қарастырайық.
1-мысал.
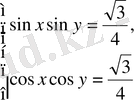 жүйесін шешу қажет.
жүйесін шешу қажет.
Шешуі: Жоғарыда айтылғандай, бұл жүйені:
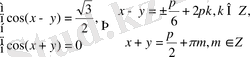 түрінде жазамыз. Осыдан
түрінде жазамыз. Осыдан
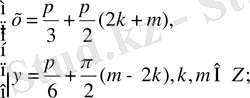
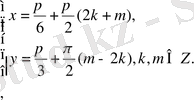
Жауабы:
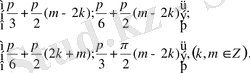
2.
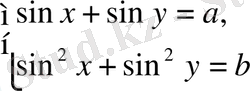 түріндегі жүйелер.
түріндегі жүйелер.
Оларды
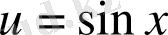 ,
,
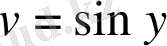 белгілеулері арқылы
белгілеулері арқылы
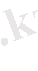
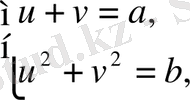

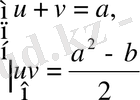
алгебралық жүйелерге келтіріп шешеміз.
2-мысал.
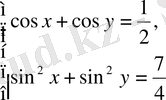 жүйесін шешу қажет.
жүйесін шешу қажет.
Шешуі:
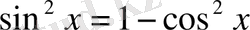 формуласын қолдана отырып, бұл жүйені
формуласын қолдана отырып, бұл жүйені
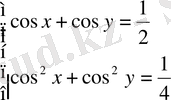
Түріне келтіріп, белгілеулері арқылы
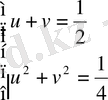 немесе
немесе
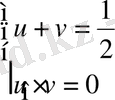 түріне келтіреміз.
түріне келтіреміз.
Осыдан,
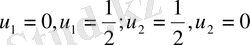 Яғни
Яғни
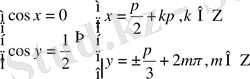 және
және
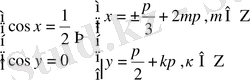
Жауабы:
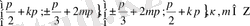
3.
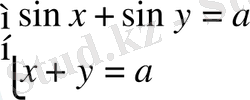 (3)
(3)
түріндегі жүйелер.
Оларды шешу үшін бірінші теңдеуін көбейтіндіге түрлендіреміз:
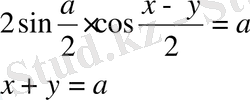 Онда бұл жүйені
Онда бұл жүйені
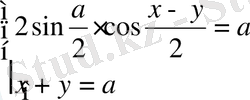 түрінде жазуға болады. Мұнда екі түрлі жағдай орындалуы мүмкін.
түрінде жазуға болады. Мұнда екі түрлі жағдай орындалуы мүмкін.
а)
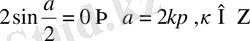 Онда
Онда
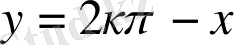
Сондықтан (3) жүйенің бірінші теңдеуінен
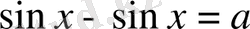 болатындығы шығады. Яғни тек
болатындығы шығады. Яғни тек
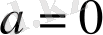 болғанда ғана (3) жүйенің шешімі бар және бұл жүйе
болғанда ғана (3) жүйенің шешімі бар және бұл жүйе
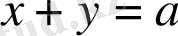 теңдеуімен мәндес.
теңдеуімен мәндес.
ә) Eгер
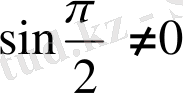 болса, онда
болса, онда
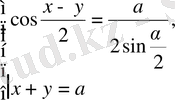
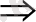
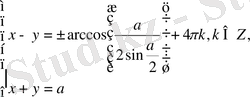
Oсыдан,
 әрине, бұл жағдайда жүйенің шешімі бар болуы үшін
әрине, бұл жағдайда жүйенің шешімі бар болуы үшін
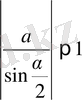 теңсіздігінің орындалуы қажет. Ал бұл шарт орындалмаған жағдайда жүйенің шешімі болмайды.
теңсіздігінің орындалуы қажет. Ал бұл шарт орындалмаған жағдайда жүйенің шешімі болмайды.
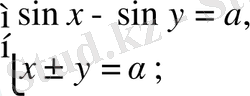
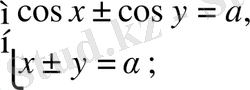
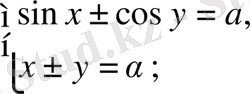 жүйелері де осы сияқты шешіледі.
жүйелері де осы сияқты шешіледі.
4-мысал:
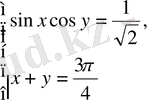
жүйесін шешу қажет.
Шешуі: Жоғарыда айтылғандай, бұл жүйені
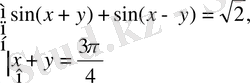

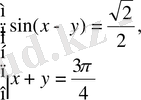
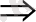
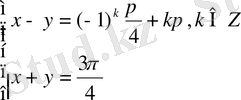
түрінде жазамыз. Осыдан
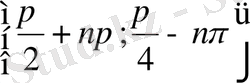 ,
,
Осы әдістерді қолдана отырып, төмендегідей жүйелерді шешуге болады:
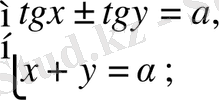
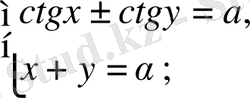
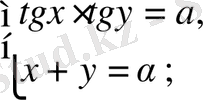
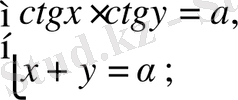
4.
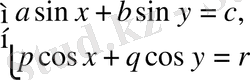
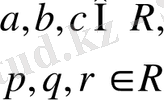 түріндегі жүйелер.
түріндегі жүйелер.
Оларды шешу үшін,
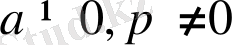 болғанда
болғанда
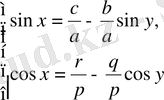
түрінде жазып, екі теңеуді де квадраттап, қоссақ, онда
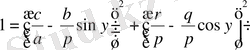 , бұл теңдеу у-ке ғана тәуелді.
, бұл теңдеу у-ке ғана тәуелді.
5-мысал.
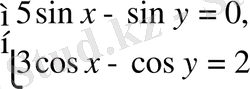 жүйесін шешу керек.
жүйесін шешу керек.
Шешуі.
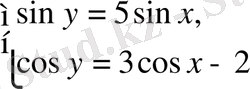
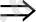
 теңдеуін аламыз. Осыдан
теңдеуін аламыз. Осыдан
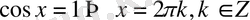 . Aл
. Aл
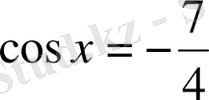 теңдеуінің шешімі жоқ. Онда
теңдеуінің шешімі жоқ. Онда
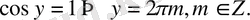
Жауабы:
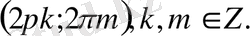
2 Тригонометриялық теңсіздіктер
2. 1 Тригонометриялық функциялардың графиктері мен қасиеттері
Енді әрбір тригонометриялық функциялардың графигін салуға тоқталайық.
1
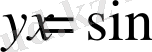 функциясын қарастырамыз
функциясын қарастырамыз
Функцияның:
1) анықталу облысы
барлық нақты сандар жиыны, яғни

2) мәндер жиыны
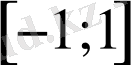 кесіндісі, яғни
кесіндісі, яғни

3)
 , функция периодты, оның ең кіші оң периоды 2п .
, функция периодты, оның ең кіші оң периоды 2п .
4) функция тақ, өйткені
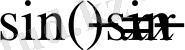 .
.
5)
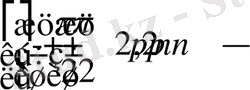 кесінділерінде функция бірсарынды өспелі,
кесінділерінде функция бірсарынды өспелі,
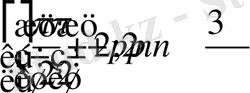 кесінділерінде бірсарынды кемімелі.
кесінділерінде бірсарынды кемімелі.
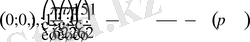 нүктелерінің координаталық жазықтыққа түсіріп
нүктелерінің координаталық жазықтыққа түсіріп
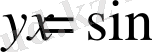 функциясының
функциясының
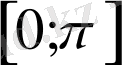 кесіндісінің графигін саламыз (4-сурет) .
кесіндісінің графигін саламыз (4-сурет) .
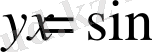 функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық. Осы қасиетті пайдаланып,
функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық. Осы қасиетті пайдаланып,
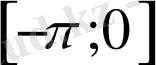 аралығында графикті жалғастырамыз. Сонда,
аралығында графикті жалғастырамыз. Сонда,
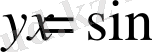 функциясының
функциясының
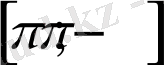 кесіндісіндегі графигін аламыз
кесіндісіндегі графигін аламыз
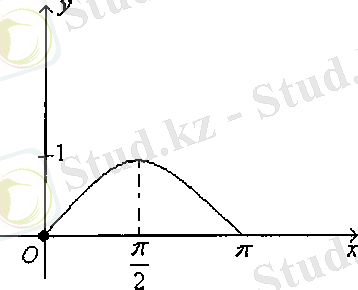
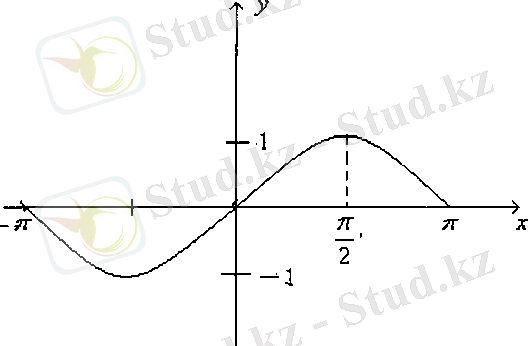
Сурет 1 Сурет 2
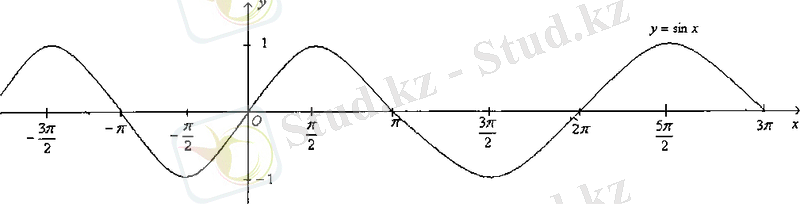 Демек,
Демек,
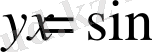 функциясының толық бір период ішіндегі графигін салдық. Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функция графигін салуға болады.
функциясының толық бір период ішіндегі графигін салдық. Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функция графигін салуға болады.
Сурет 3
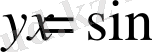 функциясының графигін синусоида қисығы деп атайды.
функциясының графигін синусоида қисығы деп атайды.
2
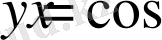 Функциясын қарастырамыз.
Функциясын қарастырамыз.
Функцияның:
1) анықталу облысы -барлықнақты сандар жиыны, яғни .
2) мәндер жиыны
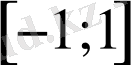 кесіндісі, яғни
кесіндісі, яғни

3)
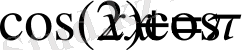 , функция периодты, ең кіші оң периоды 2π .
, функция периодты, ең кіші оң периоды 2π .
4) функция жұп, өйткені
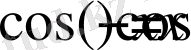
5)
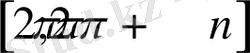 ,
,
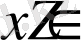 кесінділерінде бірсарынды кемімелі және
кесінділерінде бірсарынды кемімелі және
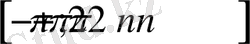
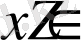 кесінділерінде бірсарынды өспелі функция.
кесінділерінде бірсарынды өспелі функция.
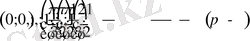 нүктелерін координаталық жазықтықта белгілеп,
функциясының
нүктелерін координаталық жазықтықта белгілеп,
функциясының
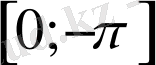 кесіндідегі графигін саламыз (7-сурет) .
кесіндідегі графигін саламыз (7-сурет) .
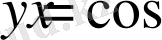 функциясы жүп функция болгандықтан, оның графигі ордината осіне қарағанда симметриялы қисық. Осы қасиетті пайдаланып,
функциясы жүп функция болгандықтан, оның графигі ордината осіне қарағанда симметриялы қисық. Осы қасиетті пайдаланып,
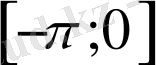 аралығында графикті жалғастырамыз. Сонда,
аралығында графикті жалғастырамыз. Сонда,
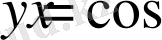 функциясының
функциясының
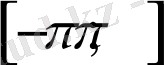 кесіндісіндегі графигін аламыз.
кесіндісіндегі графигін аламыз.
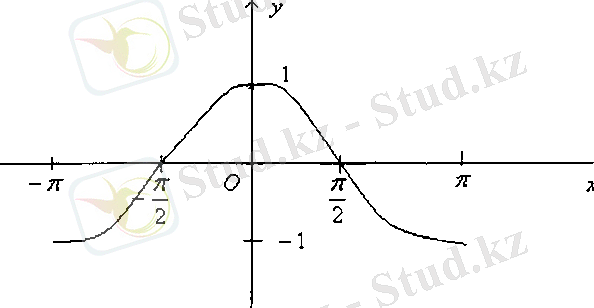
Сурет 4 Сурет 5
Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функцияның графигін салуға болады (8-сурет) .
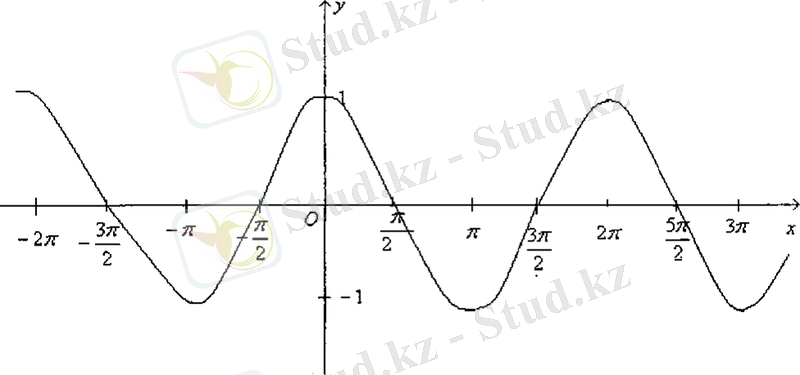
Сурет 6
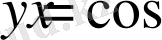 функциясының графигін косинусоида қисығы деп атайды.
функциясының графигін косинусоида қисығы деп атайды.
Сонымен қатар
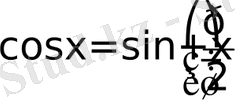 екенін ескеріп
екенін ескеріп
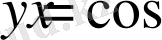 функциясының графигін
функциясының графигін
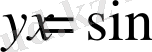 функциясының графигінен Ох осінің бойымен
функциясының графигінен Ох осінің бойымен
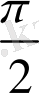 қашықтығына теріс бағытта параллель көшіру арқылы да алуға болады.
қашықтығына теріс бағытта параллель көшіру арқылы да алуға болады.
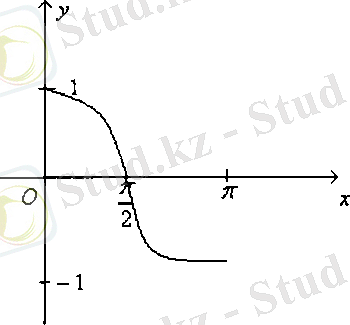
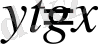 Функциясын қарастырайық.
Функциясын қарастырайық.
Функцияның:
- Анықталу облысыжиынынан басқа барлық нақты сандар
- Мәндер жиыны - барлық нақты сандар жиыны, яғни
- функция периодты π саны;
- функция тақ, өйткені
- , интервалдарында функция бірсарынды өспелі.
Енді функциясының графигін салайық.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz