Иррационал теңдеулер мен теңсіздіктер және олардың жүйелерін оқыту әдістемесі


Ирроционал теңдеулер мен теңсіздіктер, олардың жүйелерін оқыту əдістемесі
Жоспар
Кіріспе . . . 31. Ирроционал теңдеулер мен теңсіздіктердің мәні мен мазмұны
1. 1 Ирроционалдылық ғылымның қалыптасуы және тарихы . . . 5
1. 2 Ирроционалдық теңдеулер мен теңсіздіктерді анықтау . . . 7
2. Ирроционалды теңдеулер жүйелерін оқыту əдістемесі
2. 1 Ирроционалды теңдеулер мен теңсіздіктерді шешу әдісі . . . 9
2. 2 Стандартты формалардың иррационалдық теңдеулерін шешу . . . 12
Қорытынды . . . 21
Пайдаланған әдебиеттер . . . 23
Кіріспе
Курстық жұмыстың өзектілігі. Қоғамымыздың қазіргі даму қарқыны елімізде барлық салада түбегейлі өзгерістер енгізуді қажет етеді, ал бұл өзгерістерді енгізу мамандардың кәсіби даярлығының сапасының жоғары болуын талап етуде. Педагогикалық ғылымның басты міндеті - студенттерді кәсіби даярлау жүйесін жасау, оны жетілдіру құралдарын негіздеу.
Жоғары оқу орнында мұғалімді кәсіби даярлау жүйесі қоғамдық-саяси, арнайы, психологиялық-педагогикалық және әдістемелік дайындығын қамтиды.
«Мұғалім - әртүрлі типтегі жалпы білім беретін мектептерде оқушылармен оқу және тәрбие жұмысын жүргізетін маман». Мұғалім оқушыларды оқыту сапасына, олардың білім және тәрбие деңгейіне жауапты екендігі белгілі. Мұғалімнің жұмысы оның жеке тұлғасының негізгі сапаларының кәсіби іс-әрекетінің сипатына сай келген жағдайда ғана табысты болады. Мұғалім мектеп оқушысының негізгі құзырлылығын қалыптастыруға бағытталған оқу-тәрбие іс-әрекеттерін орындайды. Қазақстан Республикасының 12 жылдық білім беру жүйесі бойынша құжаттарда білім беру саясатының басым бағыттарының бірі ретінде қоғам мен мемлекет, жеке тұлғаның болашақтағы қажеттіліктеріне білім берудің барлық компоненттерін сәйкестендіру және заманауи білім сапасымен қамтамасыз ету керек екендігі көрсетілген.
Мектеп математика курсында оқушылар үшін игерілуі қиын тақырыптардың бірі ирроционал теңдеулер мен теңсіздіктер және оларды шешу. Бұл тақырыпты мұғалім жетік біліп қана қоймай, оқушыларға түсінікті, жүйелі тапсырмалар ретімен ұсынуы керек.
Курстық жұмыстың мақсаты мен міндеттері: Орта мектепте өтілетін ирроционал теңдеулер мен теңсіздіктер жан-жақты қарастырып, оны бір жүйеге келтіру мәселесін, әсіресе теориялық материалды толық меңгере отырып, берік практикалық дағды қалыптастыру мәселелерін қарастырдық.
Ирроционал теңдеулер мен теңсіздіктер теориясы оқушылардың ойлау қабілетін дамыта алатындай өз алдына ғылыми - педагогикалық маңызы бар орта мектептегі негізгі оқу материалы болып есептеледі. Ол оқушыларды айқын және дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады.
Курыстық жұмыстың құрылымы: Курыстық жұмыс кіріспе бөлімнен және үш тараудан, сонымен бірге қорытынды және пайдаланған әдебиеттер тізімінен тұрады.
1. Ирроционал теңдеулер мен теңсіздіктердің мәні мен мазмұны
1. 1 Ирроционалдылық ғылымның қалыптасуы және тарихы
«Рационал» сөзі латынамерикалық «коэффициент» сөзінен алынған. Өзгеше сандардың қатынасын білдіретін сандар ежелгі уақытта иррационалды сандар деп аталған. Бастапқыда Теодор Киренан рационал және ирроционал терминдерін симметриялы және ассиметриялылық деген болатын. V-VI ғасырларда Роман авторлары Капелла мен Кассиодор бұл терминдерді латын тіліне аударып, рационалды және иррационалды сөздермен ауыстырды. 6-шы ғасырдың бірінші жартысында рим жазушысы Боэтиус тағы бір «сметалық» (комменсурабилис) термині енгізілді.
Классикалық дәуірдің ежелгі грек математиктері тек ұтымды сандарды (өте бүтін сандар, бөлшек және оң) пайдаланды.
Үндістан, Таяу Шығыс математиктері алгебра, тригонометрия және астрономия ғылымдарын дамытты, алайда ирроционал шамаларсыз оларды толық зеріттеу мүмкін емес болатын . Ирроционал мәнін гректер «Alogos», мысалы, шаршы түбірі, ал еуропалықтар болса араб сөзінен латын тіліндегі surdus сөзіне аударды . Surdus сөзі XII ғасырдың ортасында еуропаның қараңғы(саңырау) кезінде алғашқы рет қолданылады. Белгілі аудармашы Герард Кремон математикалық атауларды араб тілінен латын латын тіліне аударды, содан кейін итальяндық математик Леонардо Фабоначий және басқа да еуропалық математиктер XVIII ғасырға дейін аударды. Жеке ғалымдар, негізінен итальяндық математик Рафаэль Вомбелли және нидерландық математик Саймон Стевин иррроционал сан ұғымын рационал сан ұғымына теңестірді. Стевин былай деп жазды: « абустырдық және ирроционалдық мәндер болмаған, бірақ бұл сандар арасында бір үйлесім бар, бұл сандар арасындағы үйлесімді біз күндіз түні ойлауымыз керек»
Бомбелли мен Стивен мен Таяу Шығыстағы елдердің көптеген ғалымдары өздерінің жазбаларында иррационалды сандарды толыққанды алгебра нысандары ретінде пайдаланды. Оның үстіне, Омар Хайям 12 ғасырдың басында Евклидтің «Принципі» туралы түсініктеме беру және Еудокстың қарым-қатынасының жалпы теориясын зерттеген кезде, санның ұғымын теориялық жағынан оң санға дейін кеңейтеді. Сол бағытта 13 ғасырдағы ұлы математик Ат-Туси көп нәрсе жасады.
Заманауи оқу құралдарында иррационалды сандарды анықтау негізі әл-Каши, Стивен және Декарттың сегменттерді өлшеуге және шексіз ондық фракциялардың идеясына негізделген. Дегенмен, нақты сандардың қасиеттері мен олардың толық теориясын негіздеу XIX ғасырда ғана дамыды.
Иррационал теңдеу - деп белгісіздері рационал таңбасы астында немесе бөлшек дәрежеге шығарған амалдардың таңбасы астында болып келген теңдеулерді айтады. Мұндай теңдеулердің негізгі қасиеттерін еске түсірейік.
Теңдеуге енетін барлық жұп дәрежелі түбірлер арифметикалық түбірлер, яғни түбір астында тұрған өрнектер тек теріс емес мәндер үшін анықталған, ал түбірдің өзі тек теріс емес мәндер ғана қабылдайды.
Теңдеуге енетін барлық тақ дәрежелі түбірлер түбір таңбасы астында тұрған өрнектің кез-келген нақты мәндерінде анықталған, түбір таңбасы астында тұрған өрнектің таңбасына қарай теріс таңбалы емес мәндерді де, теріс таңбалы мәндерді де қабылдай береді.
Иррационал теңдеу - белгісізі,
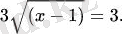 яғни айнымалы шамасы радикал таңбасының астында болатын теңдеу, мысалы, {\displaystyle ~3{\sqrt {\left(x-1\right) }}=3. }
яғни айнымалы шамасы радикал таңбасының астында болатын теңдеу, мысалы, {\displaystyle ~3{\sqrt {\left(x-1\right) }}=3. }
 . Мұны шешу үшін тендеудің екі жағын үшінші дәрежеге шығарамыз, сонда {\displaystyle ~x-1=3^{3}; x-1=27, x=28}иррационал теңдеулерді әдетте радикалдардан арылту тәсілімен шешеді. Бұл үшін тендеудің екі жақ бөлігінде тендеу рационал өрнек пайда болатындай тәсілмендәрежелеу керек. Кейде бұл жайтты бірнеше рет қайталауға тура келеді. Осы түрлендірулер нәтижесінде алгебралық теңдеу (бүтін немесе бөлшек), жалпы алғанда, бастапқы берілген теңдеуге мәндес (эквивалентті) болмай қалады. Көбінесе берілген теңдеудің салдары пайда болады. Тендеуді қанағаттандырмайтын шешімді бөгде шешім ретінде ескермейтін боламыз. Бірақ та теңдеудің екі жақ бөлігі тақ дәрежеге дәрежеленген болса, онда жаңа теңдеу бастапқы теңдеуге мәндес (эквивалентті) болады. Мына тендеулер жүбы мәндес болмайды:
. Мұны шешу үшін тендеудің екі жағын үшінші дәрежеге шығарамыз, сонда {\displaystyle ~x-1=3^{3}; x-1=27, x=28}иррационал теңдеулерді әдетте радикалдардан арылту тәсілімен шешеді. Бұл үшін тендеудің екі жақ бөлігінде тендеу рационал өрнек пайда болатындай тәсілмендәрежелеу керек. Кейде бұл жайтты бірнеше рет қайталауға тура келеді. Осы түрлендірулер нәтижесінде алгебралық теңдеу (бүтін немесе бөлшек), жалпы алғанда, бастапқы берілген теңдеуге мәндес (эквивалентті) болмай қалады. Көбінесе берілген теңдеудің салдары пайда болады. Тендеуді қанағаттандырмайтын шешімді бөгде шешім ретінде ескермейтін боламыз. Бірақ та теңдеудің екі жақ бөлігі тақ дәрежеге дәрежеленген болса, онда жаңа теңдеу бастапқы теңдеуге мәндес (эквивалентті) болады. Мына тендеулер жүбы мәндес болмайды:
- A•B=CжәнеAB=C\sqrt{A} \bullet \sqrt{B} = C\ және\ \sqrt{AB} = C
- AB=CжәнеAB=C\frac{\sqrt{A}}{\sqrt{B}} = C\ және\ \sqrt{\frac{A}{B}} = C\
{\displaystyle ~{\sqrt {A}}={\sqrt {B}}Осы өрнектердің оң жағындағы теңдеулерінің бір мезгілде {\displaystyle ~A<0} және {\displaystyle ~B<0} болған жағдайдағы шешімдері сол жақгағы тендеулердің шешімдері болмайды.
1. 2 Ирроционалдық теңдеулер мен теңсіздіктерді анықтау
Иррациоиал теңдеуді шешуде қолданылатын негізгі әдістер теңдеудің екі жағын да бірдей белгілі бір дәрежеге шығару; белгісізді ауыстыру; теңдеудің екі жағын да бірдей белгілі бір функцияға көбейту; теңдеуге енетін функцияның қасиетін және олардың графиктерін пайдалану. Көрсетілген әдістерді қолданып, кейбір түрлендірулер жасағанда, мысалы, теңдеудің екі жағын да бірдей жұп дәрежеге шығарғанда, берілген теңдеудің түбірлерінен басқа, бөгде түбірлердің пайда болатындығын ескертеміз. Сондықтан теңдеуді шығарып болған соң, бөгде түбірлерден құтылу әдістерін қарастыруымыз керек. Әдетте оны тексеру әдісі арқылы жүргізеді. Сондықтан да тексеру иррационал теңдеулерді шешудің бір кезеңі болып табылады.
Теңдеудің екі жақ бөлігін n-ші дәрежеге шығарып шешу әдісі белгілі f(x) =g ⁿ(x) теңдеуін аламыз;
Соңғы теңдеуді шешіп, табылған түбірлерді берілген теңдеуге қойып тексереміз. Иррационал теңдеудің екі жақ бөлігін бірдей дәрежеге шығарған кезде шыққан теңдеу, кейбір жағдайда, берілген теңдеуге мәндес болмайды. Сондықтан айнымалының табылған мәндерін міндетті түрде тексеру қажет.
Теңдеуді қанағаттандыратын түбірлерді теңдеу түбірлері деп атаймыз. Қанағаттандырмайтын түбірлер теңдеудің “бөгде түбірлері” деп аталады
1. Теңдеудің екі жағын бірдей дәрежеге шығару тәсілі.
1-мысал.
Шешуі: Радикалы бар өрнекті теңдіктің сол жағында қалдырып, теңдеудің қалған мүшелерін теңдіктің оң жағына шығарамыз. Сонда
Теңдеудің екі жақ бөлігін квадраттаймыз: . Осыдан немесе Соңғы теңдеудің түбірлері және .
Табылған -тің мәндерін берілген теңдеуге қойып, теңдіктің орындалатынын тексереміз:
- x1=3x_{1} = 3түбірінxx-тің орнына қойсақ, 3+3•3+7=73 + \sqrt{3 \bullet 3 + 7} = 7, 3+4=7; 7=7, 3 + 4 = 7; 7 = 7, яғни теңдік орындалады.
- x2=14x_{2} = 14, яғни14+3•14+7=7; 14+7=7; 21≠7; 14 + \sqrt{3 \bullet 14 + 7} = 7; 14 + 7 = 7; 21 \neq 7;
2-мысал: теңдеуін шешейік.
Шешуі. ; .
- Eкінші рет квадраттаймыз:144(x−1) =(29−x) 2, 144x−144=841−58x+x2, x2−202x+985=0. x1=5жәнеx2=197144(x - 1) = (29 - x) ^{2}, \ \ 144x - 144 = 841 - 58x + x^{2}, \ \ \ x^{2} - 202x + 985 = 0. \ \ x_{1} = 5\ және\ x_{2} = 197
Тексеру жүргізіп; берілген теңдеудің түбірі болатынын, ал бөгде түбір екенін аламыз. Жауабы: 5.
3-мысал:
4-мысал:
5-мысал: Тексеру арқылы бөгде түбірді анықтаймыз. Жауабы: .
2. Иррационал теңдеуді жаңа айнымалы енгізу арқылы шешу.
1-мысал: теңдеуін шешейік.
Шешуі. болады. Осыны ескерсек, теңдеуін аламыз. Шыққан бөлшек-рационал теңдеуді бүтін теңдеуге келтіреміз: бұдан .
Түбірлерді ескерсек, және теңдеулерін аламыз. Енді шыққан теңдеулерді шешеміз.
1.
2.
Тексеру: үшін
Екі түбір де теңдеуді қанағаттындырады.
Жауабы: 1, 1 ; -2, 8.
2. Ирроционалды теңдеулер жүйелерін оқыту əдістемесі
2. 1 Ирроционалды теңдеулер мен теңсіздіктерді шешу әдісі
Осы теңсіздіктерді шешкен кезде теңсіздіктердің теңсіздікті тең дәрежеде шығара алатындығын еске түсіру керек.
теңбе-тең теңсіздік.
Мысал-1: Теңсіздікті шешіңіз:
Шешуі:
Аралық әдіс арқылы жүйенің үшінші теңсіздігін шешеміз:

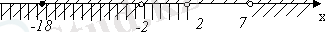
Жауабқа үш теңсіздіктің қиылысқан жерін аламыз:
Жауабы: .
Мысал-2:
Ответ: х³1.
Мысал-3:
немесе
себебі


Жауабы:
2. 2 Стандартты формалардың иррационалдық теңдеулерін шешу
Стандартты нысанның иррационалды теңдеулерін келесі ережені қолдана отырып шешуге болады:
Стандартты формалардың иррационалдық теңдеулерін шешу:
а) Теңдеуді шешіңіз
Шешімі.
2x - 1 = x 2 - 4x + 4,
x 2 - 6x + 5 = 0,
x 1 = 5,
x 2 = 1 - қарапайым түбір.
Тексеру:
х = 5,
х = 1,
Жауабы: 5 \
б) Теңдеуді шешу:
Шешуі:
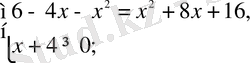
Жауабы: -1
В) Теңдеуді шешу:
х - 1 =
Шешуі:
х - 1 =
х 3 - 3х 2 + 3х - 1 = х 2 - х - 1,
х 3 - 4х 2 + 4х = 0,
х(х 2 - 4х + 4) = 0,
х = 0 немесе х 2 - 4х + 4 = 0,
(х - 2) 2 = 0,
х = 2
Жауабы: 0; 2.
г) Теңдеуді шешіңіз х -
Шешімі.
х -
х + 4 =
х 2 + 8х + 16 = 25х - 50,
х 2 - 17х + 66 = 0,
х 1 = 11,
х 2 = 6
Тексерy: х = 11, 11 -
х=6,
6-
0=0 Жауабы: 6; 11.
Аралас формалардың иррационалдық теңдеулерін шешу: • модуль белгісі бар иррационалды теңдеулер:
а) Теңдеуді шешіңіз
Шешімі.
Радикалдың нөлін ескере отырып, бұл теңдеу екі жүйеге тең:
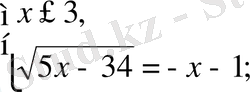

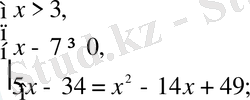
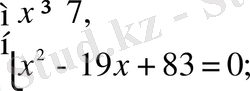

жауабы:
б) Теңдеуді шешіңіз
шешімі

Радикалдың нөлін ескере отырып, бұл теңдеу екі жүйеге тең:
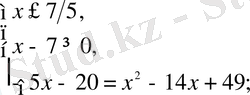
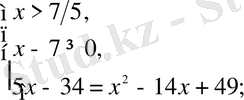
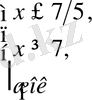
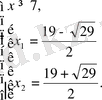
жауабы:
Итерациялық емес экспоненттік теңдеулер:
а) Теңдеуді шешіңіз
Шешімі.
ММЖ:
Енді керсінше ауытырамыз:
жауабы: 3
б) Теңдеуді шешіңіз
Шешімі.
Біз барлық дәрежені бір негізде азайтамыз 2:
бұл теңдеу мына теңдеуге тең:
Жауабы: 0, 7
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz