Типтік динамикалық буындардың жиіліктік сипаттамаларын есептеу және құру

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІ
Жәңгір хан атындағы Батыс Қазақстан аграрлық-техникалық университеті

КУРСТЫҚ ЖҰМЫС
Автоматты басқару теориясы
2-нұсқа

Тапсырған: ПС-31 топ студенті
Бакытжанова Айжан
Тексерген: а.о Джапарова Д.А

Орал-2014

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...3
1. Типтік динамикалық буындардың жиіліктік сипаттамаларын есептеу және құру ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...4
2. Жүйенің жиіліктік сипаттамаларын есептеу және құру ... ... ... ... ... ... ...9
0.1 Михайлов өлшемі бойынша тұрақтылықты анықтау ... ... ... ... ... ... ...1 3
0.2 Тұрақтылық алгебралық Гурвиц критерийі ... ... ... ... ... ... .. ... ... ... ... .14
0.3 Вышнеградский критерийсі бойынша тұрақтылықты анықтау ... ... .17
1. Тербеліс буынын табу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...18
2. Автоматты реттеу жүйесінің жиіліктік сипаттамаларын есептеу
мен құру ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...22
3. Сызықтық жүйелер тұрақтылығының анализі (ӨЖ -2) ... ... ... ... ... ... .26
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...31
Қолданылған әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... .32

Кіріспе

Басқару деп қандай - да бір үрдісті жүзеге асыруға бағытталған әсерлердің жиынтығын немесе нақты бір мақсатқа жету үрдістерінің тобын айтамыз.
Басқару техникалық жүйелер, тірі ағзалар және әлеуметтік жүйелер (экономикалық,әкімшілік, әскери) үшін қажет. Мұнда техникалық жүйелерді басқару қарастырылады.
Автоматты деп тікелей адамның қатысуымен жүзеге асырылатын басқаруды айтамыз.
Автоматты басқару жүйесі деп қандай да бір үрдісті жүзеге асыру үшін арналған құрылғылардың жиынтығын немесе тікелей адамның қатысуысыз үрдістер тобын айтамыз.
Мұндай жүйелерде адам тек қана алдыңғы қосу импульстік бере алады. Көп жағдайларда осы бастапқы импульстің өзі де автоматтың құрылғыларымен беріледі.
Автоматты реттеу жүйелері аса алуан түрлі және әртүрлі функцияларды орындай алады:автоматты қосу, тоқтау және машиналар мен механизмдердің реверсивтеу; кез - келген параметрді (жылдамдық, бағыттар, қысым, температура, тығыздық, кернеу және т.б.) берілген деңгейде автоматты түрде ұстап тұру; қандай да бір параметрдің берілген программа бойынша автоматты өзгеруі; уақыт бойынша еркін өзгеретін қандай да бір параметрді автоматты түрде көрсету (слежение).
бір немесе бірнеше параметрлерді максималды немесе минималды деңгейде автоматты түрде ұстап тұру үрдістің тиімді режимде автоматты енгізілуі.

1 Типтік динамикалық буындардың жиіліктік сипаттамаларын есептеу және құру

Жиіліктік сипаттамалар (ЖС) автоматты реттеу жүйелерін (АРЖ) анализдеу және синтездеу кезінде кең пайдаланылады. Типтік динамикалық буындардың (ТДБ) және жүйелердің жиіліктік сипаттамаларының өрнектері беріліс функциялардан (БФ) алынуы мүмкін. Ол үшін операторлық түрде жазылған беріліс функцияларында 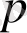операторы 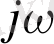ауыстырылады.
Сызықтық ТДБ немесе АРЖ кірісіне гармоникалық әсер берген кезде:

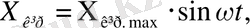(1)

ауыспалы процесс біткен кезде, шығыс сипаттаманың да түрі периодтық функция болады:
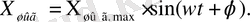(2)

Бұл функция кіріс функциясынан амплитуда және фаза бойынша ерекшеленеді, бірақ жиіліктері бірдей болады. Осы кезде ТДБ немесе АРЖ еріксіз тербеліс режимінде болады [1].

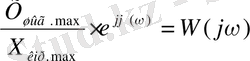(3)

қатынасы ТДБ немесе АРЖ комплексті күшейту коэффициенті деп аталады. Ол комплексті жиіліктік функциядан көрініс табады.
Осылайша шығыс шамасын комплексті жиілік функциясына кіріс шамасының көбейтіндісі деп алуға болады, яғни:

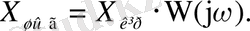(4)

W(j) өрнегін нақты P () және жорамал Q() бөліктеріне бөлуге болады:

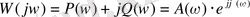(5)

мұнда: P(), Q(), A(), () - бойынша полиномдар.
Жиілік өзгерген кезде амплитуда A() және фаза () өзгереді. Олардың соңы комплексті айнымалы жазықтығында қисықты суреттейді. Ол қисық ТДБ немесе тұйық (жабық) АРЖ - ың амплитуда - фазалық жиіліктік сипаттамасы (АФЖС).

1- кесте. ТДБ-дың динамикалық параметрлерінің мәндері

Нұсқа.

Инерциялы буын
Инерция-
сыз буын
Интеграл-даушы буын
Дифференциа-лдаушы буын
Тербеліс буын

W(p)=
W (p) = K
W (p) =
W (p) = Kдp
W(p)=

2
2,8
1,2
4,0
0,4
1,8
1,0
1,2
0,2

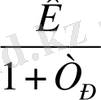
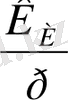
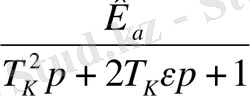
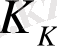
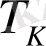
Сонымен, жиілік өзгерген кезде P, Q, A, шамалары да өзгереді. Сондықтан осы шамалар үшін де жиіліктік сипаттамаларды құруға болады. Осыған сәйкес:
P() - нақты жиіліктік сипаттама (НЖС);
Q() - жорамал жиіліктік сипаттама (ЖЖС);
Aж () - амплитудалық жиіліктік сипаттама (АЖС);
ж () - фазалық жиіліктік сипаттама (ФЖС).

Сипаттамалар арасындағы қатынас төмендегідей өрнектермен анықталады:

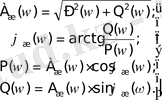(6)

Осындай сипаттамалар тұйық (жабық), ашық жүйелер үшін және ТДБ үшін алынуы мүмкін.
Жиіліктік сипаттамалар жүйенің дифференциалды теңдеулерін есептемеуге мүмкіндік береді. ЖС - ның түрі бойынша жүйенің тұрақтылығы, бірқатар сапа көрсеткіштері туралы білуге болады. Сондай - ақ ЖС бойынша, берілген динамикалық көрсеткіштерді алу үшін, жүйені түзету амалдарын (құралдарын) анықтауға болады.
2-нұсқа бойынша беріліс функциясы 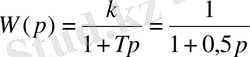болатын инерциялық буынның ЖС - ын құру қажет.
Осы буынның барлық ЖС - ның өрнегін анықтаймыз. Ол үшін беріліс функциясында Лаплас 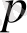операторын 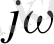- ға ауыстырамыз.
Онда:
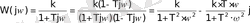. (7)
Бұл өрнектен аламыз:

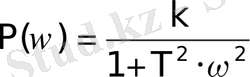- НЖС;
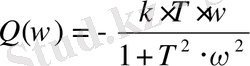- ЖЖС.

(6) өрнегін пайдалана отырып, аламыз:

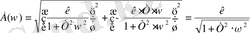- АЖС;
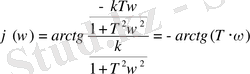- ФЖС.

Жоғарыда алынған өрнектер бойынша ЖС - дың есебін жүргіземіз.
Есептің нәтижелерін, өрнектерге алдын - ала берілген сандық мәндерді қоя отырып: 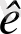=2,8 және T=1,2 с 2 - кестеге енгіземіз.

2-кесте Инерциялы буынның жиіліктік сипаттамаларының есептелген мәндері

ω
0
1
2
3
4
5
6
7
8
9
10
P(ω)=2.81+1.44ω2

2.8
1.15
0.4
0.2
0.1
0.07
0.05
0.04
0.03
0.02
0.021

Q(ω)=-3.36ω1+1.44ω2

0
-1.3
-0.9
-0.7
-0.5
-0.4
-0.3
-0.3
-0.3
-0.2
-0.3
A(ω)=P2ω+Q2(ω)

2.8
1.7
0.9
0.7
0.5
0.4
0.31
0.3
0.3
0.2
0.3
φ(ω)=arctgQP

0°
-55.8°
-73.4°
-82.3°
-85.1°
-90.1°
-91.7°
-94.1°
-90.6°
-95°
-97.2°

Инерциалы буынның жиіліктік сипаттамалыарының графиктері 1, 2, 3, 4 - суреттерде көрсетілген.
Инерциалы буынның АФЖС - ын P() және Q() мәндері бойынша декарт координатында (5 - сурет) A() және () мәндері бойынша поляр координатында құруға болады.

1 - сурет. Нақты жиіліктік сипаттама

2 - сурет. Жорамал жиіліктік сипаттама

3 - сурет. Амплитудалық жиіліктік сипаттама

4 - сурет. Фазалық жиіліктік сипаттама

5 - сурет. Декарт координатында салынған амплитуда - фазалық жиіліктік сипаттама

Басқада ТДБ - дың ЖС - лары жоғарыда берілген әдістеме бойынша құрылады.
Бұл тақырыпты баянды ету үшін студенттер ӨЖ - 1 орындайды [2].

k1=0.5 ;k2=1; kq=1.25 қабылдаймыз:

2. Жүйенің жиіліктік сипаттамаларын есептеу және құру

km; T2M; Tqжәне T1M нұсқа бойынша

Берілген нұсқа үшін сандық мағынаны есептеу арқылы:
km=11.0
T2M=0.65 с
Tq=1.4 с
T1M=0.099 с

Wpраз=k1*k2*kq*kmTq*T2M2p3+Tq-T1M+T 2M2p2+Tq+T1Mp+k2=

=0.5*1*1.25*111.40.652p3+(1.4-0.099 +0.652p2+1=

=6.8750.5915p3+0.5611p2+1.499p+1

p=jω қоямыз, өзгерте отырып мынаны аламыз:

Wjωраз=6.8751-0.5611jω2+j1.499ω-0.5 915ω3; (8)

Бөлгішке байланысты алымы мен бөлімін кешенді санға көбейтеміз және бөлеміз:

1-0.5611jω2+j1.499ω-0.5915ω3

Бұдан алатынымыз:

Wjω=6.8751-0.5611ω2-j1.499ω-0.5915ω 31-0.5611jω22+1.499ω-0.5915ω32 (9)

P ω=6.8751-0.5611ω21-0.5611jω22+1.499 ω-0.5915ω32-толық бөлігі

Qω=-6.875j1.499ω-0.5915ω31-0.5611jω 22+1.499ω-0.5915ω32-жалған бөлігі

ω
0
1
2
3
4
5
6
7
8
9
P(ω)
6.875
2.969
-1.87
-0.188
-0.051
-0.019
-0.009
-0.004
-0.002
-0.001
Q(ω)
0
-6.14
2.617
0.53
0.2
0.09
0.06
0.03
0.02
0.01

3-кесте. Есептеудің қорытындысы

6 - сурет. Нақты жиіліктік сипаттама

7-сурет Жорамал жиіліктік сипаттама

8-сурет Декарт координатында салынған амплитуда - фазалық жиіліктік сипаттама

Жүйенің тұрақтылығын Гурвиц және Михайлов өлшемі бойынша анықтау үшін тұйық ортаға арналған сипаттамалы теңдеуді табу қажет. Алшақ тұрған жүйе үшін алдын-ала тапсыру функциясы алынды.

Wp=6.8750.5915p3+0.5611p2+1.499p+1 (10)

Теріс кері байланысқан тұйықталған АС үшін тапсыру функциясы тең болады:

=6.8750.5915p3+0.5611p2+1.499p+11+6 .8750.5915p3+0.5611p2+1.499p+1=

=6 .8750.5915p3+0.5611p2+1.499p+6.875

мұндағы бөлгіш АС тұйықталған жүйесі үшін сипаттамалы есептеу болып табылады, яғни

Gp=0.5915p3+0.5611p2+1.499p+7.875=0 (11)

2.1 Михайлов өлшемі бойынша тұрақтылықты анықтаймы з

Тұйықталған АС сипаттамалы есептеуіне р операторының орнына jω мәнін қоямыз:
Gpзамк=0.5915p3+0.5611p2+1.499p+7.8 75

Gjωзамк=0.5915(jω)3+0.5611(jω)2+1.4 99jω+7.875

Gjωзамк=6.875-0.5611ω2+jω1.499-0.59 15ω2

Rω=6.875-0.5611ω2-толық бөлігі

Iω=ω1.499-0.5915ω2 - жалған бөлігі
ω Є(0,infinity) шегінде ω әртүрлі мәнін бере отырып, берудің комплексті коэффициентінің годограф нүктесінің R(ω) , J(ω) координатасын табамыз.

4-кесте Михайлов критерийсі бойынша есептеудің қорытындысы

ω
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
R(ω)
7.875
7.314
5.630
2.826
-3.102
-8.15
-14.321
-21.61
-30.03
-39.75
-50.24
-62.015
-74.92
-88.95
-104.105
-120.38
I(ω)
0
0.91
-1.734
-11.47
-31.86
-66.44
-118.77
-192.39
-290.85
-417.71
-576.51
-770.79
-1104.124
-1280.04
-1602.09
-1973.83

9-сурет Михайлов критерийсі бойынша сұлба

2.2 Тұрақтылық алгебралық Гурвиц критерийі

АРЖ дұрыс жұмыс істеу үшін ол, ең алдымен тұрақтылық шарттарын қанағаттандыру керек. Егер тұрақтылық жағдайдан шығарған қобалжу әсері алынған соң, жүйе қайтадан тұрақталған жағдайға қайтып келсе, жүйе тұрақты болады.
Сызықты жүйенің дифференциалдық теңдеудің жалпы шешімі x(t) екі уақыт функцияның қосындысы ретінде берілуі мүмкін:

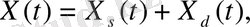(12)

мұндағы 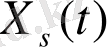- сыртқы әсерден тәуелді, жүйенің еріксіз қозғалысын сипаттайды, ал 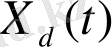- ерікті қозғалысты немесе жүйедегі ауыспалы процесті білдіреді.
Тұрақтылық шарттың математикалық түрде жазылуы дегеніміз - ауыспалы процестің басынан, уақыт шексіздікке ұмтылған кезде, 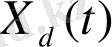нөлге айналу талабы:

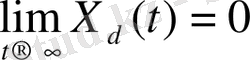(13)

ретті сызықты жүйенің дифференциалды теңдеуінің жалпы шешімі болатын 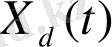функциясы келесі түрге ие [1]:

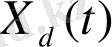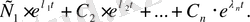= (14)

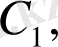
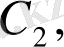
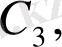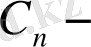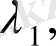
мұнда ..., интегралдау тұрақтылары, ал 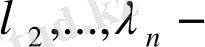басқару жүйесінің сипаттамалық теңдеуінің тең емес түбірлері. (14) өрнегінен көреміз, болғанда, 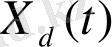нөлге қарай ынталанады егер, сипаттамалық теңдеудің барлық түбірлері теріс нақты бөлікке ие болса.
Сондықтан, АРЖ тұрақтылығы туралы пікір айту үшін сипаттамалық теңдеудің түбірлерін табу қажет емес, өйткені ол, әдетте көп еңбек сіңіруді керек қылатын есептеулермен байланысты. Жанама белгілер болса жеткілікті. Олар, сипаттамалық теңдеуде теріс емес нақты бөлігі бар түбірлер жүйесі жоқтығы туралы мәлімет береді, (нақты түбірлерді нөлдік жорамал бөлігі бар комплекстік түбірлердің дербес жағдайы деп қарастыруға болады). Мұндай белгілер тұрақтылық критерийлері деп аталады.
ретті жүйе үшін сипаттамалық теңдеу дәрежелі көпмүше түріне ие болатыны белгілі [3.4]:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.