Сандық техниканың арифметикалық және логикалық негіздері: екілік кодтау мен логика алгебрасы


МАЗМҰНЫ
КІРІСПЕ
Сандық техника екілік санау жүйесін қолданады, себебі тек екілік түрде көрсетілген сандарды өңдейді. Бірақ екілік сандарды микропроцессорлық техникада қысқа түрде жазу үшін сегіздік және он алтылық санау жүйелерін қолданады.
Санау жүйесі - бұл сандарды сандық символдармен жазу тәсілі. Санау жүйелерін позициялы және позициялы емес деп бөледі. Позициялы емес санау жүйесінде символдың мағынасы, оның санның ішіндегі орнына байланысты емес, ал позициялы санау жүйесінде байланысты.
Екілік арифметика өте жеңіл. Сандық құрылғыларда қолданылатын негізгі арифметикалық операция қосу болып табылады, себебі алуды алынатын санның таңбасын өзгерте отырып қосындыға ауыстырса болады, ал көбейту мен бөлуді - қосу мен алу операцияларына және кейбір логикалық амалдарға. Екілік сандарды арифметикалық қосу немесе алу кезінде екі логикалық 1 бір разрядта орналаса алмайтынын, яғни олар көрші жоғарғы разрядқа бір логикалық 1 ретінде көшетінін есте сақтау қажет.
1 Цифрлық техниканың арифметикалық
1. 1 Екілік кодтар
Атқарар қызметі мен күрделілігі жағынан әртүрлі цифрлық құрылғылардың (логикалық элементтерден бастап есептеу машиналарына дейін) жұмысы екілік санау жүйесінде жүзеге асырылады, яғни олардың кірістеріне түсетін және оның шығыстарынан алынатын ақпарат екілік сан түрінде көрсетіледі.
Цифрлық құрылғыларда пайдаланылатын екілік санау жүйесі позициялық санау жүйесіне жатады. Демек сандарды екілік санау жүйесінде көрсету үшін және оларға арифметикалық операциялар жүргізу үшін, өзімізге таныс, күнделікті пайдаланылатын ондық санау жүйесінің қағидалары пайдаланылады. Сондықтан алда келтірілетін, екілік санау жүйесіне байланысты түсіндірмелер ондық санау жүйесіндегі сәйкесті мәселелерді еске түсіріп, салыстырма қарастырылым арқылы жүргізіледі.
Ондық санау жүйесінде сан жазуға он символ (0 … 9) пайдаланылады (бұл жүйенің ондық санау жүйесі деп аталуы да осыған байланысты) . Бұл символдардың сандағы тұрған орнына байланысты құны (салмағы) белгіленеді: ол санау жүйесі негізінің сәйкесті разряд нөмірінің мәніндегі дәрежесі арқылы анықталады. Сонымен, санның ең кіші разрядындағы (нөлінші разрядтағы) символдың құны бір (10 0 ), келесі разрядтың (бірінші разрядтың) құны он (10 1 ), одан әрі жүз (10 2 ), мың (10 3 ) және с. с. өзгере береді. Разряд құны, мәніне сәйкесті, бірлік, ондық, жүздік, мыңдық деп және с. с. аталады, ал сан разрядында тұрған символ сәйкесті разряд құнының сан құрамына қанша рет кіретіндігін көрсетеді. Келесі мысал арқылы айтылғанды түсіндірейік:
.
Сонымен, келтірілген санның құрамында 7 бірлік, 5 жүздік, 3 мыңдық бар, ал ондық жоқ (0) .
Екілік санау жүйесінде сан жазуға екі символ (0 және 1) пайдаланылады. Разряд құны екінің (яғни санау жүйесі негізінің) сәйкесті разряд нөмірінің мәніндегі дәрежесі арқылы анықталады. Сонымен, санның ең кіші разрядындағы (нөлінші разрядтағы) символдың құны бір (2 0 ), келесі разрядтың (бірінші разрядтың) құны екі (2 1 ), одан әрі төрт (2 2 ), сегіз (2 3 ) және с. с. өзгере береді. Разряд құны бірлік, екілік, төрттік, сегіздік деп және с. с. аталады, ал екілік код разрядында тұрған символ сәйкесті разряд құнының сан құрамына қанша рет кіретіндігін, дәлірек айтқанда, бар-жоқтығын көрсетеді. Айтылғанды келесі мысал суреттейді:
.
Код құрамындағы символдардың 0 және 1 мәнінде ғана болуына байланысты, олар разрядқа сәйкесті құндық мәннің код құрамында бар-жоқтығын көрсетеді. Мысалы, келтірілген мысалдағы кодтың құрамында бірлік, екілік және сегіздік бар (1), ал төрттік жоқ (0) .
1. 2 Ондық сандардың екілік кодтары
Өзімізге үйреншікті ондық сан түріндегі ақпаратты цифрлық құрылғыда өңдеу үшін ол екілік санау жүйесіндегі сәйкесті көрсетілім түріне, яғни екілік кодқа түрлендірілуі керек. Ол үшін түрлендірілетін сан және алынған кезекті бөлінділер екіге (яғни жаңа санау жүйесінің негізіне) тізбелеп бөлінеді де, бөлінді мәні нөл болған кезде бөлу операциялары тоқтатылады; жеке бөлу операцияларында анықталған қалдықтардың шығарылым бағытына қарсы тәртіппен жазылымы осы ондық санның екілік кодын береді. Мысал ретінде ондық санау жүйесіндегі 75 санына сәйкесті екілік кодтың анықталуын көрсетелік:
75 10 = 1001011 2 .
Әрине, көрсетілген тәсілмен кез келген ондық санның сәйкесті екілік кодын анықтауға болады. Бірақ автор бұл тәсілді жеңіл тәсіл деп санамайды: біріншіден, бұндағы тізбелеп жүргізілетін бөлу операциялары ұзақ уақыт алады (мысал ретінде ондық 1000 санының екілік кодын алып көріңіз) ; екіншіден, тізбеленген бөлу операцияларының жүргізілу ұзақтығынан, қателік жіберу ықтималдығы да ұлғая түседі.
Айтылған тәсілдің кемістіктерінен құтылу мақсатында автор ондық санның екілік кодын анықтауға іс жүзінде пайдаланып жүрген өз тәсілдерін ұсынады және оның біріншісін суреттеуге алдыңғы мысалда алынған 75 саны пайдаланылады:
- алдымен алынған ондық санның құрамына кіретін екінің ең жоғарғы дәрежесіндегі санның екілік коды жазылады (64 10 = 2 6 = 1 2 , бұл санды сөз ыңғайлылығы үшін бірінші қадам коды деп аталық) ;
- келесі қадамда түрлендірілетін саннан анықталған бірінші қадам коды алып тасталады да (75 - 64 = 11), қалған санның құрамына кіретін екінің ең жоғарғы дәрежесіндегі сан анықталады (8 10 = 2 3 = 1000 2 , бұл санды екінші қадам коды деп аталық) ;
- осы тәртіппен жалғастыра отырып, ақырында өзімізге жатталымды кішігірім санның кодына жетеміз (11 - 8 = 3, 3 10 = 11 2 ) ;
- алынған бірнеше қадам кодтарын қосу арқылы қажетті код шығарылады:
Сонымен, қосу тәсілі деп аталатын бұл тәсілдің әр қадамында анықталатын кодтардың жазылымы да (1 және бірнеше нөл), олардың ақырында өзара қосылуы да оңай орындалатын операциялар болғандықтан бұл тәсіл арқылы ондық санның екілік кодын анықтау қиын болмайтындығы сөзсіз. Бірақ кейбір жағдайда бұл тәсілді одан әрі жеңілдету мүмкіндігі туады. Мысалы, 1000 санының кодын шығару үшін алдыңғы тәсілді пайдалану алты қадамға созылады (512 + 256 + 128 + 64 + 32 + 8) . Алынған сан 512-ден гөрі 1024-ке (2 10 ) жуық, сондықтан бұл жерде қажетті кодты шығару үшін 1024 санының кодынан 24-тің кодын алу жеңіл болар еді деген ой туады. Бірақ 1024-тің 1 түріндегі екілік кодынан 24 санының 11000 кодын алу тасымал арқылы жүзеге асырылатындықтан бұл оңай операция емес. 1024-тен 1 кемітілген 1023 санының коды болады және одан 23 санының 10111 кодын алу қиын еместігін осы мысалдың келесі суреттемесінен көреміз:
Сонымен, алу тәсілі деп аталатын, екінші тәсіл коды ізделінетін ондық санның екінің нақтылы дәрежелі санынан аздап кем болған кезінде пайдалануға ыңғайлы келеді. Ол келесі тәртіппен жүзеге асырылады:
- алдымен алынған ондық саннан аздап жоғары болатын екінің нақтылы дәрежесі арқылы сипатталатын саннан 1 кемітілген санның коды алынады (ол қатар жазылған бірнеше 1 арқылы жазылады және ондағы 1-дің саны дәреже мәніне тең болады) :
- бастапқы сан мен алынған кодтың ондық мәнінің айырымы анықталып, келесі қадамда екі тәсілдің ыңғайлысын пайдалану арқылы осы санның коды анықталады;
- ақырында бірінші қадам кодынан екінші қадам коды алынып, қажетті код шығарылады.
Кейбір жағдайда ондық санға сәйкесті қажетті код айтылған екі тәсілді кезектеп пайдалану арқылы алынады.
Керісінше жағдайда, яғни берілген екілік код арқылы оған сәйкесті ондық санды анықтау код жазылымындағы 1 символдарының тұрған разрядтарына сәйкесті құндарын қосу арқылы жүзеге асырылады, оны келесі мысал суреттейді:
110110001 2 = 2 8 + 2 7 + 2 5 + 2 4 + 2 0 = 256 + 128 + 32 + 16 + 1 = 433 10 .
Цифрлық құрылғылардың жұмысы екілік сандарға негізделген, бірақ пайдаланушыға мұндай сандармен жұмыс істеу (мысалы, Ассемблер тілінде бағдарлама құру кезінде) оңай жұмыс емес, сондықтан бұндай жағдайда пайдаланушының жұмысын жеңілдету үшін екілік кодтар оналтылық санау жүйесінде көрсетіледі. Жүйенің аталымына сәйкесті бұл жүйеде сан жазуға (немесе көрсетуге) он алты символ пайдаланылады, олар - 1 … 9, A, B, C, D, E, F.
Ондық санның 16-лық жазылымын, әрине, дәстүрлі тәсілмен, яғни түрлендірілетін санды он алтыға бөліп, шығарылған қалдықтарды кері бағытта жазу арқылы анықтауға болады. Бірақ оны жеңілірек келетін тәсілмен анықтауға болады:
- алдымен ондық санның екілік коды анықталады;
- алынған кодтағы символдар кіші разрядынан бастап төрт-төрттен топтарға біріктіріледі;
- әрбір топтың кодына сәйкесті 16-лық символын қою арқылы түрлендірілетін ондық санның 16-лық жазылымы шығарылады.
Айтылғанды келесі мысал арқылы түсіну қиын емес:
.
1. 3 Екілік сандармен арифметикалық операциялар
Екілік сандармен қосу операциясының жүргізілуі позициялық санау жүйесінде қабылданған тәртіппен (яғни ондық санау жүйесіндегі сияқты) жүзеге асырылады, оны келесі мысалмен суреттелік:
Екілік сандар арасындағы алу операциялары бұл сандардың қосымша кодта қосылуы арқылы жүзеге асырылады. Оң таңбалы екілік санның қосымша коды оның тура кодымен бірдей болады, ал теріс таңбалы екілік санның қосымша коды, оның разрядтарының мәнін терістеп, сосын оған бір қосу арқылы алынады. Қосымша кодпен көрсетілген санның ең артқы разрядының мәні оның таңбасын анықтайды: 0 - оң таңба, 1 - теріс таңба. Алу операциясының орындалымын екі мысалмен суреттелік:
Көбейту операциялары цифрлық жүйелерде бағдарламалы тәсілмен немесе арнайы құрылғы (аппаратты көбейткіш) арқылы жүзеге асырылады. Бөлу операциясы туралы да соны айтуға болады.
2 Логикалық функциялар
2. 1 Негізгі функциялар
Цифрлық (логикалық) құрылғылардың кірістері мен шығыстарындағы кернеу мәндері логикалық 0 немесе логикалық 1 деп аталатын екі түрлі деңгейде болады. Логикалық құрылғылардың бұл ерекшелігі оларды жобалау үшін немесе осындай дайын құрылғылардың жұмысын талдау үшін логика алгебрасының (немесе Буль алгебрасының) қағидаларын пайдалануға мүмкіндік береді.
Цифрлық құрылғылардың атқарар қызметі сәйкесті логикалық функциялар арқылы сипатталады. Күрделілігі әртүрлі кез келген логикалық функцияны негізгі логикалық функциялар деп аталатын үш функция арқылы суреттеуге болады, олар - ЕМЕС, НЕМЕСЕ, ЖӘНЕ функциялары. Олардың атқарар қызметін кесте түрінде (ол ақиқаттық кестесі деп аталады) немесе сәйкесті логикалық өрнек арқылы суреттеуге болады.
ЕМЕС функциясы - аргументіне қарсы мәнді шығаратын, бір аргументті функция (2. 1 кестені қараңыз), сондықтан бұл функция инверсия (inversion - терістеу) деп те аталады. Оның аргументі Х деп белгіленген болса, онда бұл функция Y=
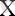 өрнегімен суреттеледі.
өрнегімен суреттеледі.
2. 1 Kесте - Y=
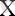 өрнегіндегі функция
өрнегіндегі функция
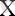

... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz