Гидростатика. Эйлердің тепе-теңдік дифференциалдық теңдеуі

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Гидростатика. Эйлердің тепе-теңдік дифференциалдық теңдеуі.
Тыныштық күйінде тұрған судың ішінен dV көлемі және dx, dy, dz қырлары бар параллелепипед таңдап алайық. Олар ox, oy және oz координаттар осіне паралель орналасқан.

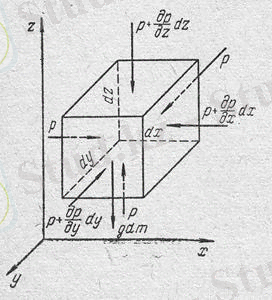
Осы параллелепипедтің тепе-теңдік теңдеулерін күштердің проекциялар теңдеуі түрінде жасайық. Статика қағидаларына сәйкес тепе-теңдіктегі қарапайым (элементарный) көлемге әсер ететін күштердің проекциясының қосындысы 0-ге тең.
Z осіне түсетін проекциялардың қосындысын қарастырайық. Бұл оське күштер проекциялайды: ауырлық, жоғарғы және төменгі қырларға әсер ететін гидростатикалық күштер.
Ауырлық күші оның массасымен dm еркін түсу үдеуінің g көбейтіндісімен көрсетіледі, яғни gdm-ге тең. Z осінің бағыты оң деп санасақ онда проекцияланатын ауырлық күші теріс болады:
-gdm = - gρdV = - ρgdxdydz.
Гидростатикалық қысымның күші төменгі қырға нормаль бойымен әсер етеді және оның Z осіне проекциясы pdxdy-е тең. Егер гидростатикалық қысымның белгілі бір нүктеде Z осімен бағытта өзгеруі dpdz-ке тең болса онда бүкіл dz қабырғаның ұзындығы бойынша ол (dpdz)dz-ке тең. Олай болса параллелепипедтің жоғарғы қырдың гидростатикалық қысымы р+(dpdz)dz-ке тең және гидростатикалық қысымның Z осіне проекциясы -[р+(dpdz)dz]dxdy-ке тең.
Z осіне түсетін барлық күштердің қосындысының проекциясы:
-ρgdxdydz+pdxdy-[р+(dpdz)dz]dxdy=0 .
Жақшаны ашып және қысқартып қойсақ келесі формула аламыз:
-ρgdxdydz+pdxdy-pdxdy-(dpdz)dzdxdy =0.
Параллелепипедтің көлемі dV=dxdydz!=0, онда - ρg-dpdz=0. Ұқсастығына қарай (ауырлық күштің проекциясының болмаған жағдайда), x және y остерге проекциясы тең болады:
-(dpdx)dxdydz=0; -(dрdy)dxdydz=0.
dV=dxdydz!=0 болғандықтан, онда -dрdх=0 және dpdy=0.
Сөйтіп қарапайым параллелепипедтің тепе-теңдік жағдайы келесі теңдеулер жүйесімен анықталады:
-dpdx=0-dpdy=0-ρg-dpdz=0
және Эйлер тепе-теңдік дифференциалды теңдеулер деген атқа ие.
Гидростатиканың негізгі теңдеуі және оның практикалық қолданылуы
Тепе-теңдік дифференциалдық теңдеулерден шығатыны, тепе-теңдікте тұрған сұйықтықтың қысымы тек қана вертикаль б-ша өзгереді. Себебі бұл теңдеулер жүйелерінде жеке туындылар dрdх және dpdy нөлге тең, сондықтан dрdz жеке туынды dpdz-ке ауыстыруға болады: -ρg-dpdz=0.
Теңдеудің екі жағын ρg-е бөліп және түрлендірсек келесі түрге келеді dz+dp(ρg)=0.
Сығылмайтын сұйықтар үшін ρg тұрақты, сондықтан d[z+p(ρg)]=0.
Интеграция нәтижесінде келесі формуланы аламыз
z+p( ρg)=const. (4.8)

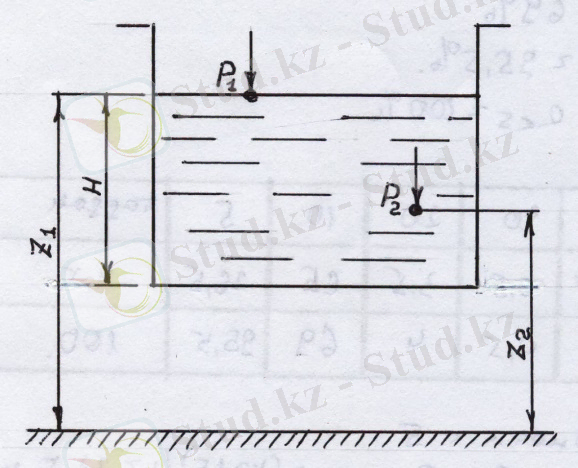
О - О жазықтықтан z1 және z2 ара қашықтықта орналасқа сұйықтықтың екі бөлшегін қарастырайық. Оларға сәйкесінше р1 және р2 қысым әсер етеді. Алдыңғы теңдеудің (4.8) негізінде келесі формула шығаруға болады:
z1+p1( ρg)= z2+p2( ρg). (4.9)
(4.8) немесе (4.9) теңдеуі гидростатиканың негізгі теңдеуі деп саналады. z өлшемі нивелирлік биіктік деп атайды, ал р(ρg) - статикалық немесе пьезометриялық тегеуірін. Демек гидростатиканың негізгі теңдеуін келесі түрде тұжырымдауға болады: тыныштықтағы сұйықтықтың әрбір нүктесі үшін нивелирлік биіктіктің және статикалық тегеуіріннің қосындысы тұрақты болады.
Гидростатиканың негізгі теңдеуінің мүшелері белгілі бір энергетикалық мағынасы бар. Мысалы, z салыстыратын жазықтыққа қатысты нүктенің орналасуынның меншікті потенциалдық энергиясын сипаттайды және геометриялық тегеуірін деп аталады, ал р(ρg) - осы нүктедегі қысымның меншікті потенциалдық энергиясын сипаттайды және статикалық тегеуірін деп аталады. Айтылған энергиялардың қосындысы сұйықтық массасының бірлігіне қатысты жалпы потенциалдық энергияны білдіреді.
Сәйкесінше гидростатиканың негізгі теңдеуі энергия сақталу заңының дербес жағдайы болып табылады: тыныштықтағы сұйықтықтың барлық нүктелерінде меншікті потенциалдық энергия тұрақты болады.
(4.9) теңдеуін келесі түрде жазуға болады
р1+ρgz1=p2+ ρgz2 немесе р1=p2+ ρg(z2-z1). (4.10)
Соңғы теңдеу Паскаль заңын білдіреді. Заңға сәйкес сығылмайтын сұйықтықтың кез келген нүктесінде пайда болатын қысым көлем бойынша барлық нүктелерге бірдей беріледі.
Гидростатиканың негізгі теңдеуі гидравликалық престердің жұмысы негізделген. Олар құрылыс материалдар өндірісінде қолданылады. Мысалы, ағаш-талшықты немесе шыныпластикалық тақтайларды, жартылай құрғақ кірпішті престегенде және т.б. материалдарды өндіру үшін қолданылады. Гидравликалық машиналар (пресстер) әр түрлі құрылыс материалдарды сынау үшін кең қолданады.

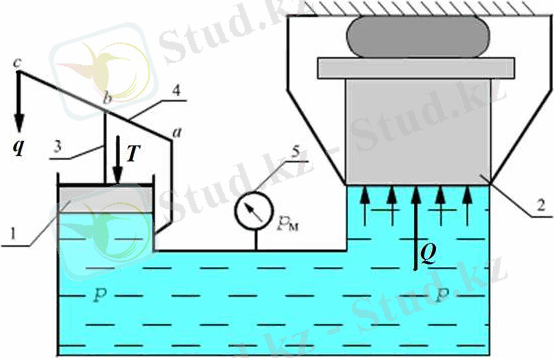
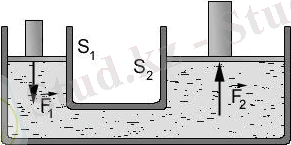
Гидравликалық пресстің принципиалдық сұлбасы
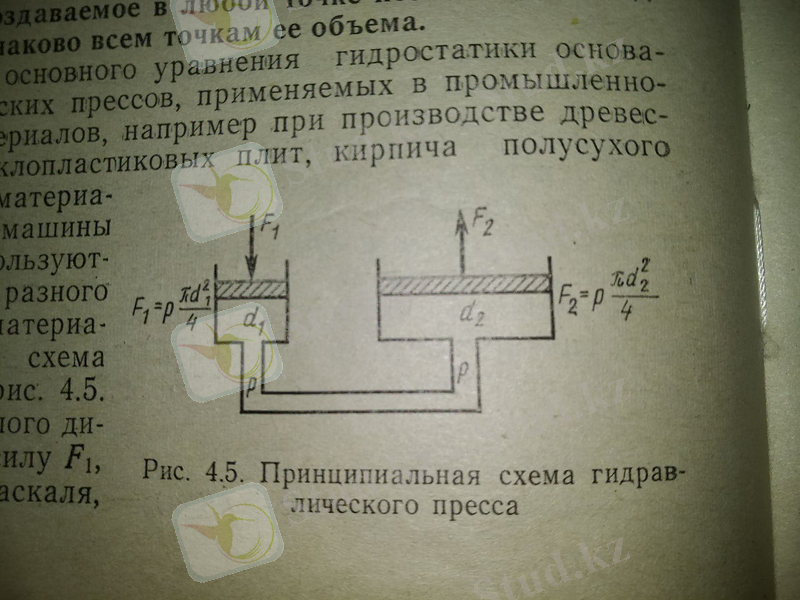
Егер кіші диаметрлі d1 поршеньге F1 күш түсірсек, Паскаль заңына сәйкес екі цилиндрдегі қысым өзара тең болады, ал d2 поршеннің ауданы d1 поршеннің ауданынан қаншалықты үлкен болса d2 диаметрлі поршеньге әсер ететін күш соншалықты үлкен болады, себебі F1=pPId14 және F2=pPId24.
Осындай тәсілмен салыстырмалы кішкентай күштің арқасында d2 диаметрлі поршень мен плитаның арасныда анағұрлым үлкен сығатын күш пайда болады.
Гидродинамика. Негізгі анықтамалар.
Гидродинамикада зерттеудің негізгі объектісі сұйықтықтың ағымы болып табылады, яғни шектететін беттердің арасындағы сұйық массаның ағысы. Ағымның қозғаушы күші қысымдардың айырымы болып табылады.
Сұйықтық қозғалысын 2 түрге бөледі: қалыптасқан және қалыптаспаған қозғалыс. Қалыптасқан қозғалыс дегеніміз сұйықтықтың жылдамдығы оның кез келген нүктесіндегі орын алатын кеңістік уақыт өтуімен өзгермейді. Қалыптаспаған қозғалыс кезінде сұйықтықтың жылдамдығы уақыт өтуімен өлшемі немесе бағыты бойынша өзгереді.
Қимасы тұрақты болып келетін құбырдың ішіндегі сұйықтықтың ағымды қарастырайық. Ағымның тірі қимасы дегеніміз сұйықтықтың қозғалыс бағытына нормальді, ағымның шектеріндегі қима. Егер ағым құбырдың қимасын толығымен алатын болса, ағымның тірі қимасы құбырдың қима ауданымен сәйкес келеді. Құбыр қимасының әрбір нүктесінде сұйықтық бөлшектерінің жылдамдығы бірдей емес: құбыр осінде көбірек болады ал қабырғаларына жақындаған сайын үйкелудің арқасында азайып келеді.
Көптеген жағдайларда ағымдардың әр түрлі нүктелеріндегі жылдамдықтарды анықтау қиындыққа соғады кейбір кезде тіпті мүмкін емес. Сондықтан инженерлік есептеулерде шынайы (локальдық) жылдамдық емес, біршама жалған орташа жылдамдықты Ʋ қолданады. Ол сұйықтықтың көлемдік шығынның V ағымның тірі қимасына S қатынасына тең:
Ʋ=VS
Немесе V= Ʋ*S
Сұйықтықтың массалық шығыны М=ρ*Ʋ*S
Сұйықтықтың массалық жылдамдығы W=ρ*Ʋ
Ағымдар тегеуірінді және тегеуірінсіз болып бөлінеді. Тегеуірінсіз ағымның беті бос болады. Мысалы каналдағы, өзендегі судың ағымы. Тегеуірінді ағым дегеніміз бос беті жоқ, каналдың тірі қимасын түгелдей алатын ағым. Мысалы су құбырындағы (водопровод) су ағымы.
Өндірістік жағдайларда су жылжитын каналдардың қимасы әр қашанда шеңберлі болмайды. Кез келген пішінді каналдардың бойымен сұйықтық қозғалғанда сызықтық өлшем ретінде гидравликалық радиус немесе эквиваленттік диаметрді қабылдайды.
Гидравликалық радиус Rг деп ағымның тірі қимасының ауданы өткізетін каналдың суланған периметірінің қатынасына тең
Rг=SP,
мұндағы S - сұйықтықтың тірі қимасының ауданы, м2
P - каналдың суланған периметірі, м.
Егер сұйықтық қимасы домалақ құбырмен толығымен толтырып жылжитын болса, онда S=PId24 және Р=PId, сондықтан Rг=(PId24)(PId)=d4.
Эквиваленттік диаметр қимасы домалақ құбыр желісінің гипотезалық (болжамдық) диаметіріне тең. Эквиваленттік диаметр ауданның А суланған периметірінің Р қатынасына тең
dэ=d=4*Rг=4AP
a және b жақтары бар тік төртбұрыш қималы канал үшін:
Rг=ab(2a+2b)=ab[2(a+b)],
dэ=4*Rг=2ab(a+b).
dэ және dн диаметрі бар қимасы шеңберлі каналдар үшін:
dэ=4(PIdн22-PIdв22)PIdн+PIdв=dн2 -dв2dн+dв=dн-dв.

Сұйықтықтың ламинарлы және турбулентті қозғалысы.
Эксперименталдық тұрғыдан табиғатта сұйықтың ағысын ламинарлық және турбуленттік деп екіге бөледі. Сұйықтың жеке қабаттары бір-бірімен қарағанда параллель, яғни сұйық қабатта бір-бірімен араласпай қозғалатын болса, онда ағысты ламинарлық ағыс (қатпарлы, ретке келтірілген) деп атайды. Сұйық бөлшектерінің жылдамдығы артып, шекті мәнге жеткенде әр қабаттардың бір-бірімен араласуы сұйықтың турбуленттік ағысы (ретке келтірілмеген) деп атайды.
Турбулентті ағында жылдамдықтың лүпілі болады. Соның арқасында ағын сызығының бойымен қозғалып жатқан бөлшектері көлденең орын ауыстырады. Бұл қарқынды араласуға әкеліп соғады. Сондықтан турбулентті қозғалыстың ламинарлыққа қарағанда энергия шығыны көбірек. Қарқынды лүпіл турбулентті ағымның өлшемі болып табылады. Жылдамдықтың лүпілі лездік жылдамдықтың ағым жылдамдығының орташа мәнінен ауытқуы болып табылады және оны бөлек құрамдас құраушыларға Δx, Δy және Δz ажыратуға болады. Олар турбулентті ағымды сипаттайды.

Ағымның осі б-ша құраушының өзгерісіне тән қасиет лездік жылдамдықтың Ʋ уақытқа тәуелдікті келесі суретте сипатталып көрсетіп тұр:

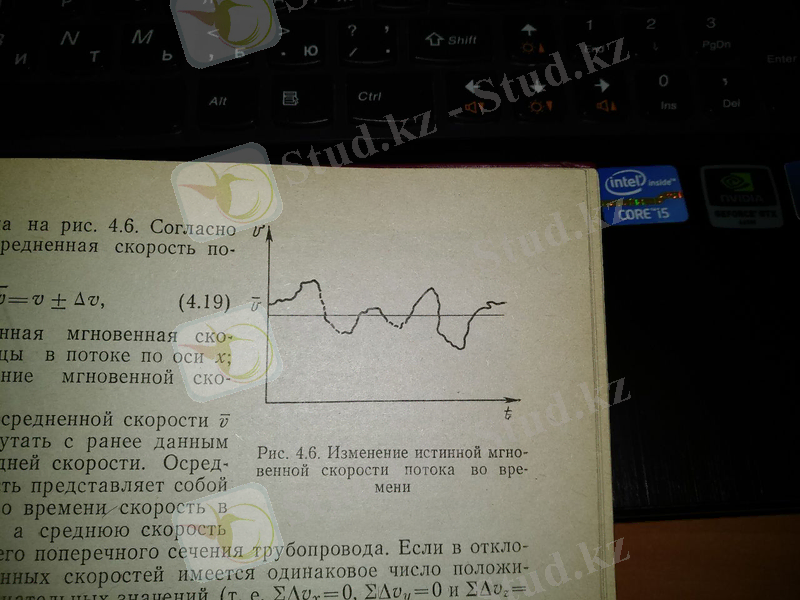
Суретке сәйкес ағымның орташаланған жылдамдығы:
Û=Ʋ+-ΔƲ,
Мұндағы, Ʋ-х осі б-ша бөлшектің шынайы лездік жылдамдығы;
ΔƲ-лездік жылдамдықтың ауытқуы.
Орташаланған жылдамдық Û түсінігін орташа жылдамдық түсінікпен шатастыруға болмайды. Орташаланған жылдамдық бір нүктедегі орташа жылдамдық емес, бұл құбыр желісінің көлденең қимасындағы ағымның орташа жылдамдығы. Егер лездік жылдамдықтың ауытқуында теріс және оң мәндердің саны бірдей болса (яғни ΣΔƲх=0, ΣΔƲу=0, ΣΔƲz=0), ағымның турбуленттігі изотропты деп айтады. Анизотропты турбулентік кезінде лүпілді жылдамдықтың барлық бағытта әр түрлі болады.
Турбулентікті турбулентті қашықтықпен сипаттайды. Ол турбуленттік ағымда бірдей жылдамдықпен қозғалып жатқан нүктелердің арасындағы ең үлкен қашықтықпен анықталады. Турбулентті қашықтық сұйықтың бүкіл көлемінде тұрақты түрде ауысып отырады және турбулентіктің масштабы ретінде қызмет етеді. Ең үлкен мәні ағымның ортасында болады себебі жылдамдық ортасында ең үлкен болады.
Турбулентті қозғалыстың маңызды сипаттамасы турбуленттік тұтқырлық болып табылады. Сұйықтықтың екі бөлшегін қарастырайық. Олар турбулентті ағында Ûх1 және Ûх2 жылдамдықпен қозғалып жатыр. Жылдамдықтың ауытқуы ΔƲх және dy ара қашықтықта орналасқан. 4.5 және 4.6 теңдеулердің негізінде келесі теңдеу шығады:
τн=-ŋd(Ûхdy)=-νρ(dÛхdy).
Ламинарлы ағын үшін бұл жанама кернеу жалғыз болатын еді және сұйықтықтың тұтқырлығын толығымен анықтайтын еді.
Турбулентті ағында х осі бойымен қозғалыстан басқа берілген бөлшектер көлденең қозғалыс жасайды. Бұл жанама кернеудің τт пайда болуын туындайды.
τт=-ŋт(dÛхdy)=-νтρ(dÛхdy).
νт шаманы турбуленттік тұтқырлық деп атайды. Оның кәдімгі тұтқырлықтан айырмашылығы сұйықтықтың қасиеті емес, ағынның параметрлеріне тәуелді - сұйықтықтың жылдамдығына, құбырдың қабырғасына дейінгі ара қашықтығы және т.б.
Ағындағы жанама кернеулердің қосындысы сұйықтықтың тұтқырлығы ретінде анықталады, сонымен қатар ағынның турбуленттілігі ретінде анықталады
τ=τн + τт = -(ŋн + ŋт) dÛхdy.
Турбулентті тұтқырлық құбыр қабырғасы нолінен (қабырғалар ағындағы бөлшектердің көлденең орын ауыстыруын азайтады) ағынның ортасындағы салыстырмалы үлкен өлшемдердің жылдамдық градиентіне пропорционалды өзгереді. Турбуленттілік үлкен болған жағдайда ŋн мәнін ескермеуге болады.
Тәжірибелердің нәтижелеріне сүйене отырып Рейнольдс сұйықтық жылдамдығының тәртібі (режимі) ағынның жылдамдығына, сұйықтықтың тығыздығына және тұтқырлығына, құбырдың диаметіріне тәуелді екендігін орнатқан. Бұл мәндер (өлшемдер) - Рейнольдс критериі Re=Ʋdρŋ деген өлшеусіз кешенге кіреді.
Қозғалыстың ламинарлық режимнен турбуленттік режимге ауысуы критерийдің Reкр ауыспалы мәні кезінде болады. Reкр мәні процестердің әрбір группаға тән. Мысалы, тік құбырдың бойымен ағынның қозғалысы Re=2300 кезінде ламинарлы режим. Ал жетілген турбуленттік режим Re104 кезінде басталады. Ирек түтіктерде (змеевик) сұйықтықтардың қозғалысы үшін Re=f(dD), араластыру үшін Re≈50, тұндыру үшін - 0,2 және т.б.
Эйлердің және Навье-Стокстың дифференциалдық теңдеулері.
Динамиканың негізгі қағидасына сәйкес қозғалыстағы сұйықтықтың көлеміне әсер ететін күштердің проекциясының қосындысы сұйықтықтың массасымен үдеудің көбейтіндісіне тең. Қарапайым параллелепипедтің көлеміндегі сұйықтықтың массасы dm=ρ dxdydz.
Сұйықтықтың Ʋ жылдамдықпен қозғалған кезде оның удеуі dƲdt, ал координаттар осіне проекциясы dƲхdt, dƲydt, dƲzdt. Көлемі dV=dxdydz қарапайым паралелепипедке ауырлық күші және қысым әсер етеді. Бұл күштердің координат остеріне проекциясы келесі болады:
-dpdx*dxdydz; -dpdy*dxdydz; -(ρg*dpdz)*dxdydz;
Ньютонның екінші заңына б-ша (F=ma), динамканың негізгі қағидасына сәйкес,
ρ*dxdydz* dƲхdt=-dpdx*dxdydz;
ρ*dxdydz* dƲydt=-dpdy*dxdydz;
ρ*dxdydz* dƲzdt=-(dpdz+ρg)*dxdydz;
dxdydz қысқартсақ келесі теңдеу шығады
ρ*dƲхdt=-dpdx;
ρ*dƲydt=-dpdy; (4.42)
ρ*dƲzdt=-ρg-dpdz;
(4.42) теңдеулер жүйесі Эйлердің идеалды сұйықтық қозғалысының дифференциалдық теңдеулер болып табылады.
Ағындағы нақты сұйықтықтың қозғалысы кезінде қысым және ауырлық күштерінен басқа үйкеліс күші әсер етеді. Сондықтан (4.42) теңдеуі толықтырылуы қажет.
Тамшылы сұйықтықтың қарапайым көлемінің қозғалысы кезінде жылдамдықтың Ʋх проекциясы көлденең жазықтыққа дейінгі ара қашықтыққа тәуелді. Жанама кернеулер dA бетте паралелепипедтің қырларында пайда болады.
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.