N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді шешу әдістері

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 44 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министірлігі
Ш. Уәлиханов атындағы Көкшетау мемлекеттік университеті ШЖҚ РМК

Тасболат Бекзат

N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифферен-циалдық теңдеулерді шешу әдістері.

ДИПЛОМДЫҚ ЖҰМЫС

Мамандығы 5В010900-Математика

Көкшетау 2018
Қазақстан Республикасы білім және ғылым министірлігі
Ш. Уәлиханов атындағы Көкшетау мемлекеттік университеті ШЖҚ РМК

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді шешу әдістері.

Мамандығы 5В010900-Математика

Орындады: ________________________ Тасболат Б.

Ғылыми жетекші,
п.ғ.к., доцент: ________________________

Қорғауға жіберілді

Кафедра меңгерушісі _________________

Көкшетау 2018

МАЗМҰНЫ

КІРІСПЕ

1 N-ШІ РЕТТІ, КОЭФФИЦИЕНТТЕРІ АЙНЫМАЛЫ БІРТЕКТІ СЫЗЫҚТЫҚ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР

1.1 Жоғары ретті дифференциалдық теңдеулер ... ... ... ... ... ... ... ... ... ... ... ...
1.1.1 Жоғары ретті дифференциалдық теңдеулерді интегралдаудың тәсілдері
1.2 N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

2 N-ШІ РЕТТІ, КОЭФФИЦИЕНТТЕРІ АЙНЫМАЛЫ БІРТЕКТІ СЫЗЫҚТЫҚ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ ӘДІСТЕРІ.

2.1 Дифференциалдық теңдеулерді шешудің жуықтау әдістері ... ... ... ... ... .
2.2 Дифференциалдық теңдеулерді қатарлардың көмегімен жуықтап интегралдау
2.2.1 Дәрежелік қатардың көмегімен дифференциалдық теңдеулерді
интегралдау . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. ... ... ... ... .
2.2.2 Гипергеометриялық теңдеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2.2.3 Бессель теңдеуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. ... ... ...
2.3 N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді жалпыланған Абель формуласын пайдаланып шешу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
2.4 Эйлер теңдеуі ... ... ... ... ... .

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. ... ... ... ...63

ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 64

КІРІСПЕ

Зерттеу тақырыбының өзектілігі:
Механиканың, математикалық физиканың, инженерлік ғылымдардың, сондай-ақ білімнің көптеген салаларын зерттеу дифференциалдық теңдеулерді интегралдауға алып келеді. Ал дифференциалдық теңдеулерді интегралдау түптеп келгенде математикалық анализдің классикалық әрі маңызды сұрақтарының бірі екендігі белгілі.
Болашақ математика пәнінің мұғалімдерін даярлауда пәндер арасындағы сабақтастық пен пәнішілік байланыс өте маңызды. Жоғары оқу орындарында мемлекеттік стандартқа сай математиканың түрлі салаларын оқытуда, оның іс жүзінде қолданылуына айрықша мән беріледі. Айталық, дифференциалдық теңдеулерді шешуді оқып үйренгенде, оның практикалық маңызы ескеріледі және оны шешуде басқа пәндермен байланысы, сабақтастығын білу маңызды. Ол үшін, математиканың барлық тарауларын толық қанды меңгеру керек. Алайда соңғысы, математиканың салаларын толық оқып-меңгеру, математика мамандығында оқитын студенттер үшін де, сағаттардың тапшылығына байланысты, мүмкін болмай отыр. Қазір, бұл мәселелерді шешудің бір жолы ретінде өзіндік жұмыстар, өзіндік оқулар ұсынылуда. Соның бір көрінісі, дипломдық жұмыс болып табылады. Оқу бағдарламасынан тыс қалатын тақырыптарды терең меңгеру үшін, дипломдық жұмыстың тақырыбын N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді шешу әдістері деп таңдадым.
Диплом жұмысының мазмұны n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулердің түрлеріне және олардың шешу әдістеріне арналған.
Жұмыс кіріспеден, негізгі екі тараудан және қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады. Бұл тарауларда жоғары ретті дифференциалдық теңдеулердің толық классификациясы мен n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулер-дің түрлеріне тоқталып және оларды интегралдаудың әдістері туралы баяндалады.
Жұмыстың мақсаты: n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулерді шешу әдістерін көрсету.
Жұмыстың міндеті: n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулердің түрлеріне және оларды шешу әдістеріне байланысты мысалдарға тоқталу.

N-ШІ РЕТТІ, КОЭФФИЦИЕНТТЕРІ АЙНЫМАЛЫ БІРТЕКТІ СЫЗЫҚТЫҚ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР

1.1 Жоғары ретті дифференциалдық теңдеулер
[1]-[3]

Анықтама.
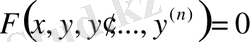(1)
түріндегі теңдеу n - ретті дифференциалдық теңдеу деп аталады, мұндағы x-тәуелсіз айнымалы, ал у=у(х)-ізделінді функция.
Егер (1)-ден n - і туынды табылатын болса, онда

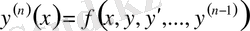(2)

теңдеуі ең жоғары туындысы арқылы шешілген n - ретті дифферен-циалдық теңдеу деп аталады.
Коши есебі:

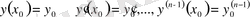(3)

бастапқы шарттарды қанағаттандыратын (2) дифференциалдық теңдеудің шешімін табалық.
Теорема (Коши есебі шешімінің бар және оның жалғыз болуы туралы).

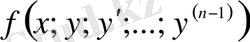функциясы

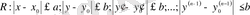
облысында мына екі шартты қанағаттандырсын делік:
1) 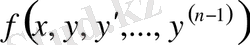функциясы өздерінің аргументтері бойынша үзіліссіз және шенелген:

;

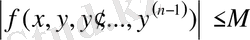2) функция үшін айнымалылары бойынша

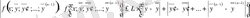
Липшиц шарты орындалады.
Липшиц шарты функциядан айнымалылары бойынша алынған үзіліссіз дербес туындылары бар болғанда ғана орындалады, онда анықталған, өзінің n - і туындыларымен қоса үзіліссіз және (3) бастапқы шарттарды қанағаттандыратын жалғыз 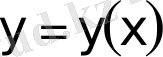шешімі бар болады.
Бұл теореманы жеңілдеу тұжырымдауға болады.
Егер (2) дифференциалдық теңдеудің оң бөлігі үзіліссіз, шенелген және бойынша үзіліссіз дербес туындылары болса, онда Коши есебінің жалғыз шешімі бар болады.
Анықтамалар.

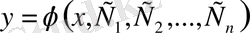
функциясы (2) дифференциалдық теңдеудің жалпы шешімі деп аталады, егер ол:
1) 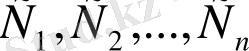-дың кез келген мәндерінде (2) дифференциалдық теңдеуді қанағаттандырады;
2) берілген (3) бастапқы шарттар бойынша 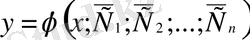функциясы (3) бастапқы шарттарды қанағаттандыратын мынадай 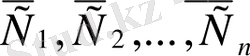-і табуға болады.
Егер жалпы шешімінде 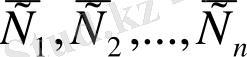-ң нақты мәндері алынатын болса, онда функция дифференциалдық теңдеудің дербес шешімі деп аталады.

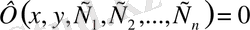
түріндегі қатысы, мұндағы 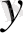айқын берілмеген, (2) дифференциалдық теңдеудің жалпы интегралы деп аталады
(2) теңдеуді интегралдау үшін бастапқы шарттарды қанағаттандыратын жалпы шешімін немесе дербес шешімін табу қажет.

1.1.1 Жоғары ретті дифференциалдық теңдеулерді
интегралдаудың тәсілдері

1. Тәуелсіз айнымалы және жоғары туындысы бар теңдеулер.

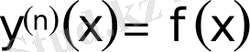
түріндегі теңдеуді қарастырамыз.
Екі бөлігін де 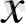бойынша интегралдаймыз:

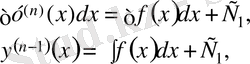
тағы да интегралдаймыз:

.

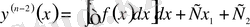Осы тәсілмен n рет интегралдаймыз, сонда

.

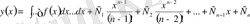1-ші түрдегі n-ретті ДТ тізбектей n рет интегралдау тәсілімен шешіледі.
Мысал.
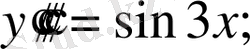теңдеуін шешелік.

;

;

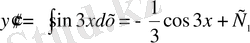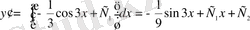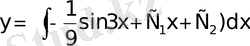
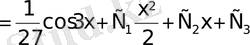
2. у функциясы және оның (k-1)-і ретіне дейінгі туындылары жоқ теңдеулер.

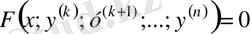
түріндегі ДТ қарастырамыз.
Жаңа айнымалы енгіземіз:

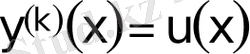, (4)

сонда

u(х) функциясы мен оның алынған туындыларын қарастырылатын (4)
теңдеуге қоямыз, сонда:

.

Сонымен, 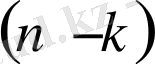- ретті теңдеу алынды, яғни ДТ-ң реті төмендетілді. Жаңа ДТ-ң шешімі

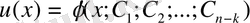
функциясы болсын делік. Мұны (4) теңдеуге қоямыз:

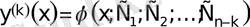
- k ретті дифференциалдық теңдеу аламыз, ал бұл k рет дифферен-циалдау арқылы шешіледі (1-түрдегі теңдеу).
Мысалдар. 1.
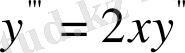үшінші ретті ДТ шешелік.

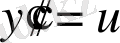ауыстыруын алайық, 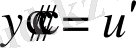. Бұларды теңдеуге қою арқылы

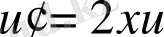бірінші ретті ДТ-і аламыз. Айнымалыларын ажыратамыз:

;

.

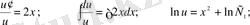
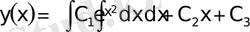Бұл теңдеу квадратурада шешіледі.
2. ;
;
;
;
;

;
;
;

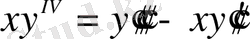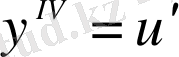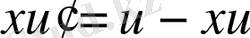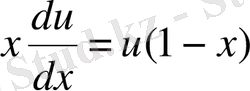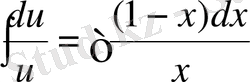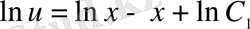бұл теңдеуді бөліктеп үш рет интегралдау арқылы шешу керек (1-түрі)

3. Тәуелсіз айнымалы х-і жоқ теңдеулер.

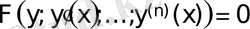
түріндегі теңдеуін қарастырамыз.
Тәуелсіз жаңа айнымалы үшін у-ті аламыз және ауыстыру орындаймыз:

.

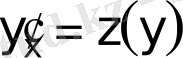Екінші, үшінші және т.б. туындыларын алу үшін осы жаңа функциядан күрделі функция есебінде туынды табамыз:

;

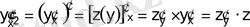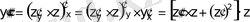
және т.б.
Табылған туындыларды теңдеуге қойып, реті бірге кеміген ДТ аламыз:

.

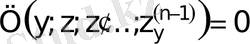Шешімі мына түрде табылды делік:

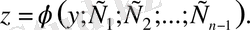
Енді ауыстыруға қайта оралып айнымалылары ажыратылған бірінші ретті ДТ аламыз:

.

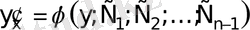Мысал. 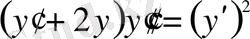ДТ шешелік. Мұнда тәуелсіз айнымалы х жоқ.

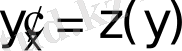ауыстыруын орындаймыз.

;
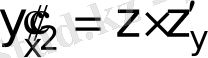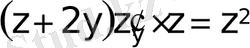- бұл біртекті теңдеу.

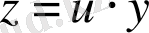- ауыстыруын аламыз,

.
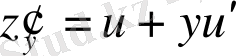Теңдеуге қоямыз:
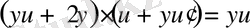. у-і қысқартамыз:

.

;
;
;

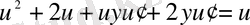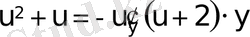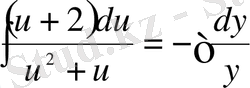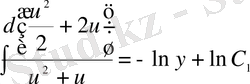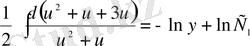- біртекті теңдеудің шешімі

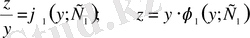
немесе

,
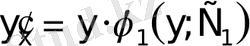ал бұл айнымалысы ажыратылған ДТ.

4. Сол бөлігі толық туынды болып келген теңдеулер.

теңдеуін қарастырамыз және

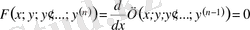
болсын делік. Жаңа дифференциалдық теңдеудің екі бөлігін де интегралдаймыз, сонда
.

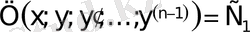ДТ реті бірге төмендеді.
Мысалдар. 1
.
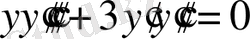Бұл 3-ші түрдегі теңдеуі.
4-ші түрдегі тәсілімен шешіп көрелік.
,
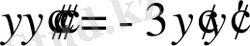екі бөлігін де
-ке бөлеміз:

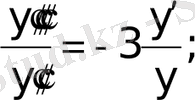
енді интегралдаймыз:

;

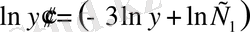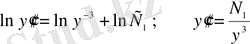- теңдеудің х-і жоқ.
;
;
;
;
;
;
;

;

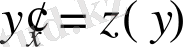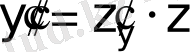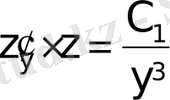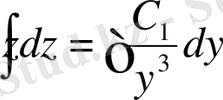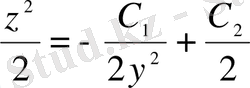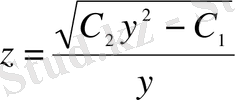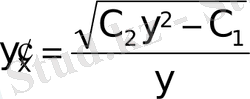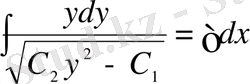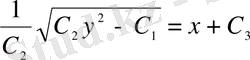
бұл үшінші ретті ДТ жалпы интегралы, сондықтан оның үш еркін тұрақтысы бар.
2. ;

;
;

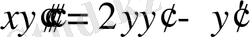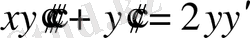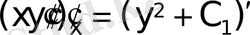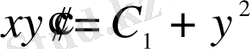бұл ДТ реті бірге төмендеді.

3. .

;

;

;

;

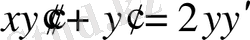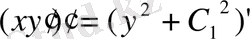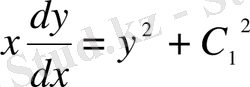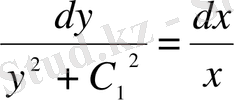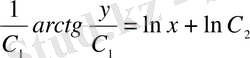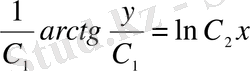- бұл ДТ жалпы интегралы.

1.2 N-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеулер

Анықтама.

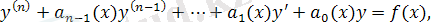(1)

түріндегі дифференциалдық теңдеулер n-ретті сызықтық дифферен-циалдық теңдеулер (СДТ) деп аталады, мұндағы 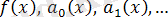. -берілген үздіксіз функциялар.

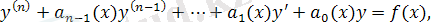(2)

теңдеуі коэффициенттеріне байланысты, тұрақты коэффициентті және айнымалы коэффициентті болып екіге бөлінеді. Оң жағындағы функция 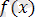0-ге тең болса, біртекті деп, ал 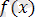0-ге тең болмаса біртекті емес деп аталады. Біздің қарастыратынымыз n-ші ретті, коэффициенттері айнымалы біртекті сызықтық дифференциалдық теңдеу.

операторы

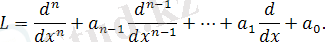(3)

формуласымен айқындалған. Сонда, (1) теңдеуді, мына түрде қайта жаза аламыз:

(4)

операторының сызықты екеніне оңай көз жеткізуге болады:

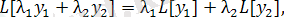(5)

мұндағы λ1 және λ2 -еркін тұрақтылар. Бұл өз кезегінде, егер у1 және у2 функциялары теңдеудің дербес шешімдері болса, онда олардың сызықтық комбинациясы да

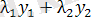
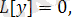(6)

теңдеудің шешімі болады.

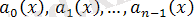функциялары нақты болған жағдайды қарастырамыз. Егер

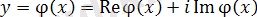(7)

комплекстік функциясы (6) біртекті теңдеудің шешімі болса, онда функцияның нақты және жорымал бөліктері де, (6) теңдеудің шешімі болады.
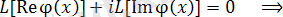
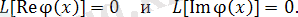
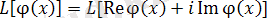Шынында, операторының сызықты болғандықтан және комплекс
сандардың қасиетінен шығады.
(5) теңдеудің барлық шешімдерінің жиыны теңдеудің фундаментальді шешімдер жүйесі деп аталады.
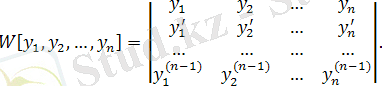Вронский анықтауышы (немесе вронскиан) мына формуламен анықталады:
Теорема. Вронский анықтауышы (а,в) аралығының ең болмағанда бір нүктесінде 0-ге тең болмаса, онда λ1, λ2,.. λn айнымалылары бойынша n сызықтық теңдеулер жүйесін аламыз:

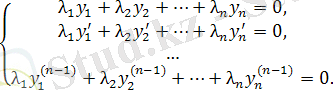
(10)

Крамер теоремасы бойынша, коэффициенттерінен тұратын матрицаның анықтауышы 0-ге тең болмаса, бұл жүйенің шешімі бар және ол жалғыз болады. Мұндай анықтауыш ретінде Вронский анықтауышын айта аламыз, ол теореманың шарты бойынша 0-ге тең емес. Демек берілген жүйенің шешімі жалғыз.

Wy1,y2,..., yn=y1 y2 ...y1 y2...⋯ ... .. ynyn... y1n-1y2n-1 ...ynn-1(11)
1-Мысал.
1,x,x2,..., xn-1 функциялары сызықтық тәуелсіз, себебі, Вронский анықтауышы 0-ге тең емес.

W=1xx2 ...xn-1 012x ...n-1xn-1 00x ...n-1n-2xn-2 ... ... . ... .. 000 ...n-1! =1!*2!*...*n-1!

2-Мысал. ek1x,ek2x, ..., eknx функциялары сызықтық тәуелсіз болады, егер k1, k2, ..., kn коэффициенттері жиынында, бір-біріне тең сандар болмаса.
Шынында, егер анықтауыштың бағаналарынан ортақ көбейткішті шығаратын болсақ, онда

W=k1 ek1x ek2x ...ek1x k2ek2x...⋯ ... .. eknxkneknx... k1n-1ek1xk2n-1ek2x ...knn-1ek2x=

=ek1, k2, ..., knx1 1 ...k1 k2...⋯ ... .. 1kn... k1n-1k2n-1 ...knn-1

Оң жағындағы анықтауыштың мәні, Вандермонд анықтауышы деген атпен мәлім. Ол 0-ге тең емес көбейткіштердің көбейтіндісіне тең:

1=ij=nkj-ki

Теорема (Ly=0 сызықтық біртекті теңдеудің жалпы шешімінің құрылымы туралы) y1,y2,..., yn функциялары n-ші ретті сызықтық біртекті теңдеудің шешімінің фундаментальді жүйесін құрасын. Онда бұл теңдеудің жалпы шешімі мына түрде болады:
y=C1y1+C2y2+...Cnyn
мұндағы, C1, C2, ..., Cn -еркін тұрақтылар.
Дәлелдеу. Берілген оператордың сызықтылығынан,
y=C1y1+C2y2+...Cnyn функциясы Ly=0 жүйесінің шешімі болады. Төмендегі шарттарды қанағаттандыратын Коши есебінің шешімі

yx0=z0y'x0=z0'...yn-1x0=z0n-1 (12)

мұндағы, zx-жүйенің кез келген шешімі.

z0=zx0, z0'=z'xn, z0n-1=zn-1x0 (13)

теңдеуді n-1 рет дифференциалдап, Коши шарттарын тексереміз. Сонда:

C1y1x0+C2y2x0+...+Cnynx0=z0C1y1'x0+ C2y2'x0+...+Cny'nx0=z0'...C1y1n-1x0 +C2y2n-1x0+...+Cnynn-1x0=z0n-1(14)

Табылған n сызықтық теңдеуден және C1, C2, ..., Cn белгісіздеріне байланысты алгебралық жүйе, ал матрица коэффициенттерінен тұратын анықтауышы ол вронскиан, ол теорема шарты бойынша 0-ге тең емес. Олай болса, Крамер теоремасы бойынша бұл жүйе үйлесімді және жалғыз шешімі бар. Дәлелдеу керегі де осы.
Төменде 2-ші ретті айнымалы коэффициентті сызықтық біртекті теңдеудің шешімі туралы теореманы қарастырамыз.
Теорема. Егер y1 x
y''+pxy'+qxy=0
2-ші ретті айнымалы коэффициентті сызықтық біртекті теңдеудің шешімі болса, онда y2x функциясы да оның шешімі болып табылады және ол төмендегіше айқындалады:
y2x=y1xe-Fxdxy12x
мұндағы, Fx px-коэффициентінің алғашқы функцияларының бірі.
Fx=pxdx
Дәлелдеу. Шарты бойынша:

y1''+pxy1'+qxy1≡0

y1x және y2x функциялары сызықтық тәуелсіз болсын, және y2x-де шешімі болғандықтан,
y2''+pxy2'+qxy2≡0

Теңдеудің бірін y2-ге, екіншісін y1-ге көбейтіп, азайтамыз, сонда төмендегі теңдеуді аламыз:

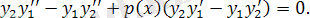
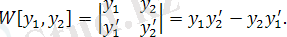Вронскиан құрайық:

Соңғы теңдеуді дифференциалдасақ:
онда берілген теңдеудің түрі төмендегідей:

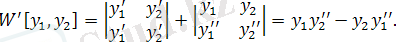
dWW=-pxdx, шешімін табу үшін интегралдаймыз, сонда:
lnW=-pxdx=-Fx
W=e-Fx,
y1y2'-y2y1'=e-Fx,

y1y2'-y2y1'y12=1y12e-Fx,

y2y1''-y1y2''+pxy2y1'-y1y2'=0

Wy1,y2=y1y2y1'y2'=y1y2'-y2y1'

W'y1,y2=y1'y2'y1'y2'+y1y2y1''y2''=y 1y2''-y2y1''.

W'+pxW=0

y2y1'=1y12e-Fx,

y2y1=e-Fxdxy12x,

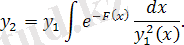
Теорема толық дәлелденді. Осы теоремадан шығатын салдары және оның қолданыстары туралы жұмыстың 2.3 бөлімінде қарастырамыз.

2 N-ШІ РЕТТІ, КОЭФФИЦИЕНТТЕРІ АЙНЫМАЛЫ БІРТЕКТІ СЫЗЫҚТЫҚ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ ӘДІСТЕРІ.

2.1 Дифференциалдық теңдеулерді шешудің жуықтау әдістері

Анық теңдеулердің тек қана бөлек көпсандық емес класы квадратураларда интегралданaды (немесе, аналитикалық жолмен шешіледі). Ғылым мен тәжірибенің қажеттіліктерінен туындаған көптеген теңдеулер элементар функциялар класында немесе квадратуралардада нақты шешілмейді. Сондықтан да мұндай теңдеулердің жуықталған шешімдерін табу туралы есебі туындайды. Дифференциалдық теңдеулердің жуықталған шешімін құру әдісі дифференциалдық теңдеулерді интегралдаудың жуықталған әдісі деп аталады.
Жуықтау әдісі Ньютон мен Эйлер жұмыстарында бастау алды. Қазіргі кезде дифференциалдық теңдеулердің шешімінің жуықталған әдісінің теориясы жеткілікті дамыған және дифференциалдық теңдеулер теориясымен қатар шынайы объектілер мен процесстерді зерттеудің математикалық аппараты болып табылады.
Дифференциалдық теңдеулердің шешімдерінің жуықталған әдісінің теориясы екі бағытта дамыды: дифференциалдық теңдеулерді интегралдау-дың аналитиикалық жуықталған әдісін құруда және дифференциалдық теңдеулердің шешімдерінің сандық әдістерін құруда.
Аналитикалық жуықталған әдістердің кең таралған түрі асимптотикалық әдіс. Олар дәлдік дәрежесі айнымалысы кейбір бастапқы нүктеден тәуелсіз ағымдағы мәнінен жоғары дифференциалдық теңдеулердің жуықталған шешімін құруға мүмкіндік береді.
Дифференциалдық есептердің шешімінің сандық әдісі Эйлер жұмысында бастау алды. Онда бірінші сандық әдіс - Эйлердің сынық әдісі - қалыпты теңдеулер үшін Коши есебінің шешімі. Есептеу математикасының дифференциалдық теңдеулердің шешудің сандық әдісінің теориясы математикалық пәннің негізгі бөлігі болып табылады. Сондықтан мұнда бұл әдістер қарастырылмайды. Қазіргі кезде сандық әдістер күрделі дифференциалдық теңдеулерді шешудің негізгі әдісі болып отыр. Бұл әдістердің рөлі күннен күнге артып келеді, әсіресе кибернетиканың дамуында және есептеу техникасы мен осыған байланысты есептеу процестерін автоматтандыруда, технологияны, өндірістік және басқа да күрделі процесстерді басқару мүмкіндіктерінде.
Мұнда анық теңдеулердің интегралдаудың асимптотикалық әдісінің негізгі түрлерін қарастырамыз. Бұл әдістер функцияларды асимптотикалық жуықтауға негізделеді. Дифференциалдық теңдеулерді шешудің асимптотикасын құруда дәрежелік қатар әдісі (регулярлы және сингулярлы), аздық параметр әдісі (регулярлы және сингулярлы), сонымен қатар дифференциалдық теңдеулердің асимптотикалық әдісі қарастырылады.
Дәрежелік қатар әдісі. Дәрежелік қатар әдісі - бұл дифференциалдық теңдеулердің шешімін дәрежелік қатарға жіктеу немесе айнымалыдан тәуелсіз дәрежелері бойынша көпмүшелікке немесе осы айнымалының кейбір функцияларының дәрежесі бойынша. Берілген дифференциалдық теңдеулерді шешуде дәреженің тегістігіне байланысты регулярлы және сингулярлы әдістер ажыратылады. Осы әдістерді қарастыруға келейік.
Дәрежелік қатардың регулярлы әдісі. -ші ретті айқындалған дифференциалдық теңдеуді қарастырайық:

(1)

және бастапқы немесе қосымша шарттарды

(2).

Егер (1) теңдеу аналитикалық түрде интегралданбаса, онда (1), (2) есептерін шешу мүмкін емес. Сондықтан да мұндай жағдайда (1) теңдеуге жуықталған шешімі кез-келген параметрлерде жататындай етіп интегралдаудың жуықталған әдісін қолдану қажет. Бұл параметрлер есебінде кейіннен қосымша (2) шартты қанағаттандыратын жуықталған шешімдер алынады.
Олай болса, функциясы аналитикалық және айнымалысына тәуелсіз өзгеру және ұйғарылған айнымалының

облыстарында жеткілікті тегіс, көрсетілген (1) теңдеудің жуықталған шешімін құруда дәрежелік қатардың регулярлық әдісі немесе сәйкесінше көпмүшеліктерді қолдануға болады. Мұның негізінде егер (1) теңдеудегі функциясы кейбір нүктесінің аймағында аналитикалық болса, онда теңдеудің шешімі аналитикалық функция болатын нүктесінің аймағы бар болады; егер функциясы көрсетілген аймақта рет үздіксіз дифференциалданса, онда сәйкесінше нүктесінің аймағындағы шешімі рет үздіксіз дифференциалданады. Бірінші жағдайда ізделініп отырған шешім Тейлор қатарына жіктеледі:

, (3)
екінші жағдайда Тейлор формуласымен берілген

(4)
мұндағы

(5)
- Тейлор коэффициенті, -қалдық мүше.
Олай болса, (3) теңдеудің нақты шешімін және (1) теңдеудің жуықталған шешімін

(6)
құру үшін (5) Тейлор коэффициенты есептеу қалды. (3), (4) жіктеу шешімді түзу координаталық жіктеу деп аталады. Ізделінді коэффициенттері коэффициенттерінің алғашқы арқылы өрнектеледі, мұнда коэффициенттерінің алғашқы -нен коэффициенттеріне тәуелділігі (1) теңдеуінің көмегімен анықталады. Шынында да,

(7)

және тағы басқа.
Өзіміз көріп отырғанымыздай, Тейлордың әрбір коэффициенті , алдыңғы коэффициенті арқылы өрнектеледі, ал соңында олардың барлығы коэффициентінен бастап бастапқы коэффициенттері арқылы өрнектеледі, олай болса (1) теңдеудің жалпы шешімінің кезкелген тұрақтысының рөлін ойнайды. (1) сызықтық теңдеуі жағдайында бұл жолмен оның жалпы шешімін құруға болады:

, (8)

мұндағы операторының фундаментальды матрицасы,

,
- теңдеудің дербес шешімі [16].
(1) теңдеудің осылай құрылған шешімін (2) қосымша шартқа қойып, Тейлордың бастапқы коэффициентінен тәуелді теңдеудің соңғы жүйесін аламыз. Алынған жүйені шешіп, осы коэффициенттерді табамыз.
Бұл айтылғандардан көретініміз, берілген әдіс (1) теңдеу үшін Коши есебін құру үшін ыңғайлы, егер (2) бастапқы шарт мына түрда берілсе:

, (9)

ізделінді еркін тұрақтылар берілген, ал қалған барлық Тейлордың коэффициенттері (7) формула бойынша есептелуі мүмкін.
(1)-(2) есептерді шешудің айтылған әдісі дәрежелік қатардың сингулярлы әдісі деп аталады.
№1 есеп. Коши есебінің жуықталған шешімін құр:

.

Мұнда жуықталған шешімді (6) түрінде іздейміз, мысалы -ні қою арқылы, яғни мына түрде

,

Олай болса,

.

(9)-ға сәйкес аламыз, ал (7)-ге сәйкес

Сонда

Өзіміз көріп отырғандай қарапайым теңдеулер жағдайында да Тейлордың коэффициентін құру қиын. Сондықтан да (3) қатардың коэффициенттерін құруда анықталмаған коэффициенттерді табу әдісі тиімдірек. Мұның негізінде (1) теңдеудегі функциясының тегістігі туралы қабылданған болжамдар жалпы шешім нүктесінің аймағында сәйкесті теңдеудің тегістіктің дәрежелері бар болады және бүтін көрсеткішті функциялар жүйесі сызықты тәуелсіз. (1) теңдеуге (3)-ті қойып, мынадай тепе-теңдікті аламыз:

(10)

Бұл теңдіктің оң жағын дәрежесі бойынша Тейлор қатарына жіктеп,

екі дәрежелік қатарды аламыз. Бұл қатарлардың коэффициенттері ізделінді (3) қатардың коэффициенттері болып табылады, мұнда бұл функцияның сол жақ бөлігінде ізделінді (5) қатардың коэффициенті жатады, ал оң жақ бөлігінде табылған . (10) тепе-теңдіктен көрсетілген тәсіл бойынша тепе-теңдіктің коэффициенттерін анықталмаған коэффициенттер әдісі арқылы бірдей дәрежелері бойынша теңестіріп, (7) түріндегі рекуррентті жүйені аламыз.
Анықталмаған коэффициенттер әдісін қолдану дәрежелік қатарлардың әдісін жеңілдетеді, егер мұнда функциясын Тейлор қатарына стандартты жіктеу қолданылса [17].
№2 есеп. Коши есебінің шешімін құру қажет.

Мұнда . Теңдеудің шешімін (5) түрінде іздейміз, яғни

Бұл шешімді теңдеуге қойып, мына тепе-теңдікті аламыз:

Бұл өрнекте коэффициенттерді айнымалысының бірдей дәрежелері бойынша теңестіріп және ізделінді коэффициентіне қатысты рекуррентті теңдеулер жүйесін аламыз.
Бұл жүйеден

яғни болғанда .
Бұдан

.

Қарастырылып отырған есептің нақты шешімінің алынатынын көру қиын емес.
(1) теңдіктегі функциясы аналитикалық емес, ал рет үздіксіз дифференциалданатын болса, (10) тұжырымының орнына осы әдіспен мына тұжырымды аламыз:

(10')

мұндағы - (6) теңдеуінің жуықтатылған шешімі, - қалдық мүше. Бұл жерде функциясын нүктесінде центрімен Тейлор қатарының формуласы түрінде жазып және қалдық мүшелерді қалдырып, көпмүшелердің екі қатардың тұжырымын аламыз. Бұл теңбе-теңдіктен ізделінді коэффициентке қатысты теңдеулер жүйесін аламыз.
Қарастырылып отырған дәрежелік қатардың регулярлы әдісін жалпы түрдегі -ші ретті барынша тегіс функциясымен айқын теңдеулер үшін қолданамыз.

Бұл жағдайда аналитикалық функциясының дәрежелік қатарлар әдісі (1) теңдеудегі секілді компонентті қолданылады, ал функциясының рет үздіксіз дифференциалданатын жағдайында ізделінді жуықтатылған шешімнің компонентін анықталмаған коэффициенттерімен -шы дәрежелі көпмүше ретінде құруға болады.
Бастапқы нүктелер аймағында (1) теңдеудегі функциясы үзілетін жағдайды қарастырайық. Бұл жағдайда теңдеудің шешімін құру үшін жалпыланған дәрежелік қатарлар деп аталатын, ал мұндай қатарлардың көмегімен дифференциалдық теңдеулердің шешімін құру әдісі дәрежелік қатарлардың сингулярлы әдісі деп аталады [18].
Дәрежелік қатарлардың сингулярлы әдісі. функциясы жеткілікті тегіс болғандағы дәрежелік қатардың регулярлы әдісін

(11)

теңдеуіне қолданамыз. Егер бұл орындалмаса, онда ізделінді шешімнің нүктесінде кейбір ерекшелігі бар екенін күту қажет болады. Сондықтан да бұл жағдайда дәрежелік қатардың сингулярлы әдісі қолданылады. Қарапайымдылық үшін (11) скалярлы теңдеуін қарастырайық. Дәрежелік қатардың сингулярлы әдісіне сәйкес (11) теңдеудің шешімін мына түрде іздейміз:
(12)
немесе мына түрде
(13)

(12)-(14)-тегі белгісіз параметрлерді табу үшін белгісіз коэффициенттер әдісі қолданылады. Теңдеу үшін (12)-(14) шешімдерінің формасын оның қойылымынан соң белгісіз параметрлерді анықтауға болатындай етіп таңдап алуға болады.
жағдайын қарастырайық. Дәрежелік қатарлардың сингулярлы әдісі бойынша шешімі айнымалысының теріс дәрежесінің қатары түрінде ізделінеді. Мұдан формальды шешім асимптотикалық қатарларға жинақты немесе жинақсыз болуы мүмкін, яғни

(15)

қатарына немесе жалпыланған асимптотикалық қатарға

(16)

немесе жалпыланған қатар түріне

(17)

(15)-(17) түріндегі қатарлар шешімнің кері координаталы жіктеуі деп аталады.
Аз параметрлер әдісі. Аз параметрлер әдісі параметрлерге тәуелді дифференциалдық теңдеулердің шешімін құру үшін қолданылады. Егер теңдеудің шешімі регулярлы түрде құрылса, онда аз параметрлер әдісі регулярлы деп аталады, кері жағдайда аз параметрлердің сингулярлы әдісі деп аталады.
Аз параметрлердің регулярлы әдісі. Аз параметрлердің регулярлы әдісінің екі вариантын қарастырайық. Бірінші варианттың құрылымын Пуанкаре-Ляпунов құрған, соған сәйкес Ляпунов-Пуанкаре әдісі деп аталады. Екінші вариант теңдеудің шешімінің периодты шешімін құру үшін Крылов-Боголюбов қарастырған, сондықтан да Крылов-Боголюбов әдісі деп аталады.
Ляпунов-Пуанкаре әдісі. Параметрлерге тәуелді

облысында

(1)

теңдеуін қарастырайық және бастапқы шарттарымен берілсін:

(2)

Егер облысында функциясы айнымасылы бойынша аналитикалық болса және D облысында х айнымалысы бойынша үздіксіз болса, онда облысында функциясы аналитикалық болса, онда (1)-(2) есептерінің шешімін параметрі бойынша белгісіз коэффициенттермен - тәуелсіз айнымалы функциялы қатар түрінде іздейміз. Белгісіз коэффициенттерді белгісіз коэффициенттер әдісі көмегімен іздейміз. Аз параметрлер әдісі негізі болып Пуанкаре теоремасы табылады.
(1) скалярлы теңдеуіне және скалярлы аз параметр жағдайына тоқталайық. Онда мынаны аламыз:
, (3)
, (4)
мұндағы - ізделінді коэффициенттер, - белгілі коэффициенттер; функциясын мына түрде береміз:

. (5)

(3) теңдікті (5) және (1)-ге қойып, ал (3) пен (4)-ті (2)-ге қойып, мына тепе-теңдікті аламыз:

, (6)

. (7)

(7) теңбе-теңдіктен ізделінді функциясы үшін бастапқы шартты аламыз:

(8)

(7) теңбе-теңдіктегі коэффициенттерді бірдей дәрежесі бойынша теңестіріп, рекуррентті дифференциалдық теңдеулер жүйесін аламыз:

(9)

Бірінші теңдеу (1) теңдеуі болып табылады, ал қалған теңдеулер ізделінді функциясына қатысты сызықты.
Крылов-Боголюбов әдісі. Дифференциалдық теңдеулердің жуықтатылған периодты шешімдерін Ляпунов-Пуанкаре әдісі бойынша құру периодты емес түріндегі секулярлы деп аталатын мүшелердің туындауы мүмкін. Бұл қосымша зерттеуді талап етеді [19].
Бұл жағдайда аз параметр бойынша жіктеуді құруда Крылов-Боголюбов әдісі қолданылады. Бұл әдістің қарапайым бірінші схемасы Ван дер Поль құрған болатын. Стационарлы квазисызықты теңдеу мысалында Ван дер Польдың әдісін көрсетейік.

(10).

= 0 болғанда туындайтын теңдеуінен нөлдік периодты жуықтауды аламыз:

Ван дер Поль бұл периодты шешімде А амплитуда мен фазасы жай өзгеретін функциялар екенін болжаған және оларды

теңдеуінен табуымыз қажетті.
Бұл әдістің негізі мен дамуын Крылов пен Боголюбов берген, нәтижесінде бұл әдіс Крылов-Боголюбов деп аталды. Бұл әдістің идеясын (10) теңдеуде түсіндіреміз.

= 0 болғанда теңдеудің шешімі мына түрде болады:

,

мұнда A , -фазалық бұрыш, - const. Бұл функциялар теңдеуінің шешімі болып табылады. Сондықтан да болғанда (10) теңдеудің шешімі мына түрде болады:
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.