Лежандр түрлендіруі және мультифрактал спектрі: f(α) мен D_q функцияларының параметрлік байланысы

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 2 бет
Таңдаулыға:

Лежандр түрлендіруі

Енді f ( α ) функциясы мен τ( q ) функциясы арасындағы байланысты табайық. Ол үшін Z ( q, δ ) статистикалық қосындыны есептеуіміз керек . (26) теңдікке ықтималдылық мәнін 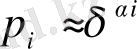қойып, және i бойынша қосындыны, (42) ықтималдық тығыздығы α бойынша интегралдап есептесек, келесі өрнекті аламыз

. (46)

δ өлшемі өте кішкене болғандықтан, бұл интегралға дәрежелік көрсеткіштері qα - f ( α ) минималды болатын (интеграл астындағы функция максимал болады) α ( q ) мәндері басты үлес қосады. Бұл қосылған үлес, интеграл астындағы функцияның максимум нүктесіндегі мәніне пропорционал болатындығы айқын. Ал α ( q ) мәні төмендегі шарттан анықталады

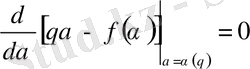. (47)

Минимум шартынан

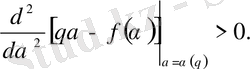(48)

Нәтижесінде α ( q ) тәуелділігі келесі теңдіктен айқын емес түрде анықталады:

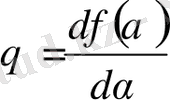(49)

және f ( α ) функциясы барлық жерде дөңес болып келеді

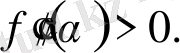(50)

Бұл α ( q ) мәнін (46) интегралға қойып, статистикалық қосындының өрнегін аламыз.

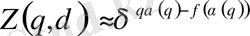. (51)

Бұл f ( α ( q ) ) өлшемі, q дәрежелік көрсеткіштің берілген мәндерінде (46) статистикалық қосындыға басым үлес қосатын, ℒ _α _{(

q

)} ішкі жиынның фракталдық өлшемділігін анықтайды.

(51) және (26) теңдіктерді салыстыра отырып, біз келесі тұжырымға келеміз

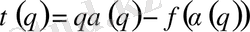. (52)

Осыдан (24) теңдік көмегімен D _q функциясын табуға болады

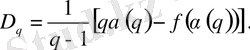(53)

Осылайша, егер біз f ( α ) мультифракталдық спектр функциясын білсек, (49) және (53) теңсіздіктері арқылы D _q функциясын таба аламыз. Және керсінше, D _q біле отырып келесі теңдеудің көмегімен α ( q ) тәуелділігін таба аламыз

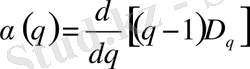(54)

және содан кейін (53) формуладан f ( α ( q ) ) тәуелділігі табылады. Бұл екі теңдеу параметрлік күйде f ( α ) функциясын анықтайды.

(54) қатынасын дәлелдеу үшін (52) теңдеуді α бойынша диференциалдайық

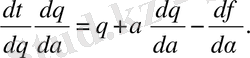(55)

Егер 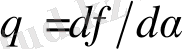екенін ескерсек, және бұл теңдікті қысқартсақ, (54) теңдеуге эквивалентті келесі қатынасты аламыз

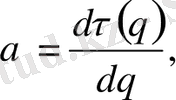(56)

(52) және (56) теңдіктері, 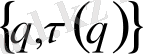және 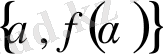айнымалылары арасындағы Лежандр түрлендіруін береді.

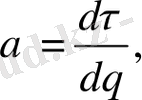
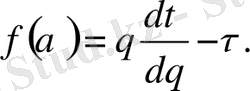(57)

Лежандрдың кері түрлендіруі (49) және (51) формулаларымен анықталады

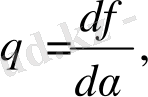
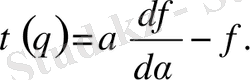(58)

f(α) функциясының қасиеттері

α әртүрлі мәндері үшін f ( α ) функциясын зерттейік. (52) теңдік бойынша 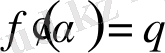, ал q = 0 болған жағдайда f ( α ) функциясының туындысы нөлге айналады. Осыған сәйкес, f ( α ) функциясы кейбір 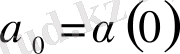нүктесінде өзінің максимуміне ие болады ( f ( α ) функциясы барлық жерде дөңес болады) . Біртекті фрактал үшін D _q = D = const . Сондықтан 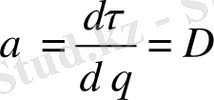және 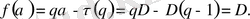Бұл жағдайда ( α, f ( α ) ) жазықтығындағы f ( α ) функциясы тек бір ғана ( D, D ) нүктесінен ғана тұрады.

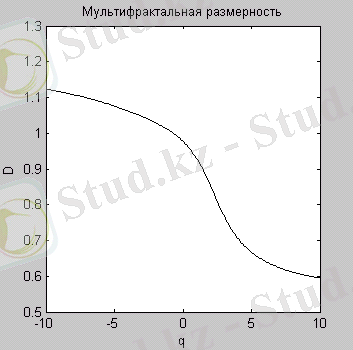
Мысал үшін, D _q жалпыланған фракталдық өлшемділіктің спектрін және f ( α ) функциясын бізге таныс логикалық бейнелу үшін есептейік (12 а сурет) . Төменде осы есептеулерге арналған бағдарлама келтірілген.