Сандар тізбегінің шегі

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

РЕФЕРАТ

Тақырыбы: Сандар тізбегінің шегі

Курс:

Группа:

Орындаған:

Тексерген:

Мазмұны:

1. Нақты сандар тізбегі және оның шегі.

2. Шегі бар тізбектердің қасиеттері.

3. Ақырсыз кішкене және ақырсыз үлкен сандар.

4. Монотонды тізбектер.

Қорытынды

Пайдаланылған әдебиет

Нақты сандар тізбегі және оның шегі.

Нақты сандар жиыны деп барлық- натурал, бүтін, рационал және иррационал сандардан құралған сандар жиының атаймыз. Және бұл жиынды Z әрпімен белгілейміз.

Натурал сандар жиынында анықталған $f$ функциясының мәндерін сан тізбегі немесе тізбек деп атайды.

Анықтама: Шексіз көп эмементке ие болған Х топтың элементтерін нөмерлеп оларды номерлері өсуі бойынша бір қатарға жазғандағы өрнекке тізбек дейіледі. Тізбектің элементері тұрақты сандар болса оған санды тізбек, ал айнымалы болса функцияналдық тізбек дейіледі. Тізбек $\left\{ х_{n} \right\}$ мен белгіленеді.

Мысалдар. 1)

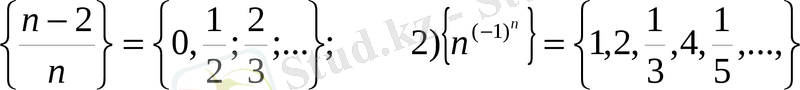
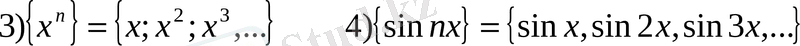
1, 2-сандық тізбектер, 3, 4, функционалдық тізбектер.

Анықтама: Егер бірар n> $N_{e}$ ден бастап тізбектің барлық мүшелері үшін теңсіздігі орындалса онда а санына $\left\{ х_{n} \right\}$ тізбектің шегі деп аталады. Ол 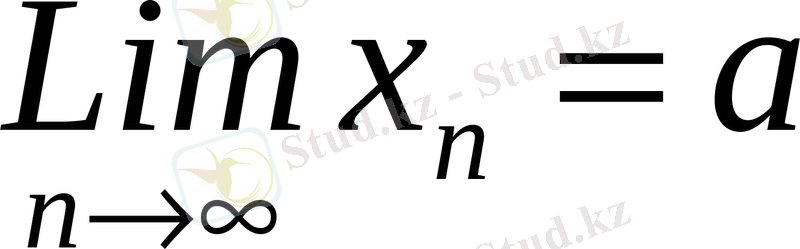немесе $x_{n} \rightarrow a\$ арқылы белгіленеді.

Мысал. 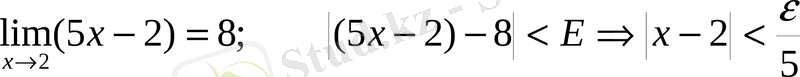теңсіздігін қанағаттандырушы барлық Х тер үшін f(x) =5x-2 нің мәні $\varepsilon$ нен кіші болады.

n артып барған сайын x-тің мәндері a-ның (a-E, a+E) маңайы ішінде a-ға ұмтылады.

Шегі бар тізбектердің қасиеттері.

1. Егер { $x_{n}$ } тізбектің шегі бар болса, онда ол шек жалғыз.

2. Егер $\left\{ x_{n} \right\}$ тізбегі жинақты болса, онда ол тізбек шенелген.

3. Егер $x_{n} \in \lbrack a, b\rbrack\ \ \$ $\lim_{n \rightarrow \infty}{\neq 0 \in \lbrack 0, 1\rbrack}$ lim $x_{n} = c \in \lbrack a, b\rbrack$ $x_{n}\frac{1}{n + 1}, \ \in \lbrack 0, 1\rbrack$

4. Егер 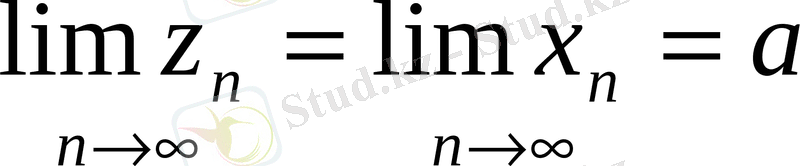болып 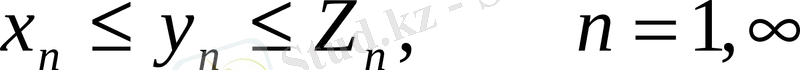болса онда 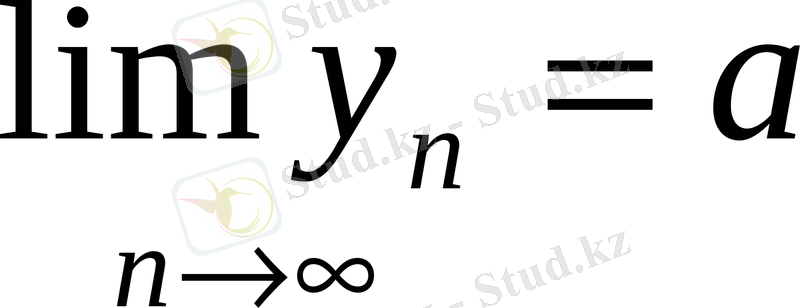болады.

Ақырсыз кішкене және ақырсыз үлкен сандар.

Анықтама. Шегі хх0 де нөлге ұмтылушы (х) ақырсыз кішкене шама деп аталады.

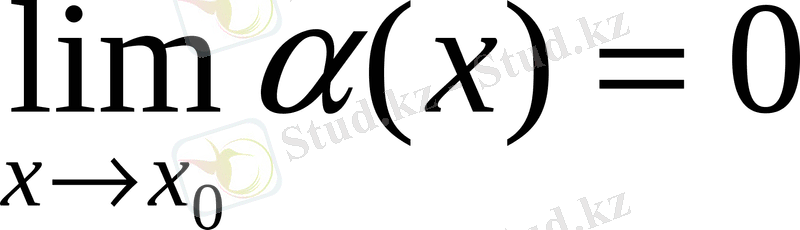
Мысалы: ; ; ; ;

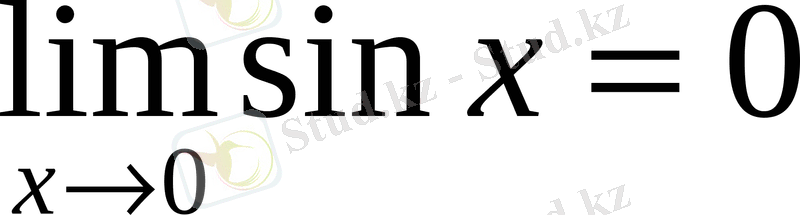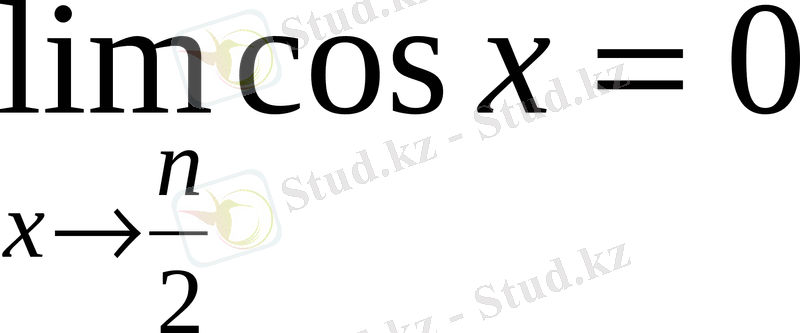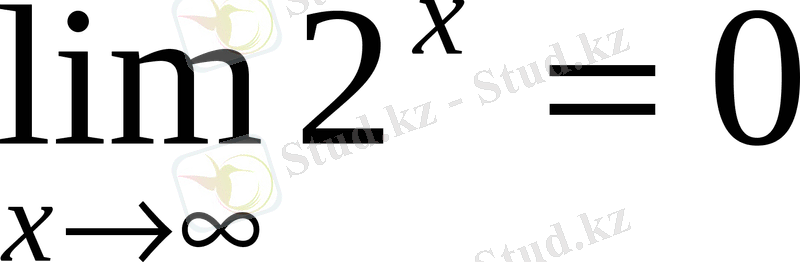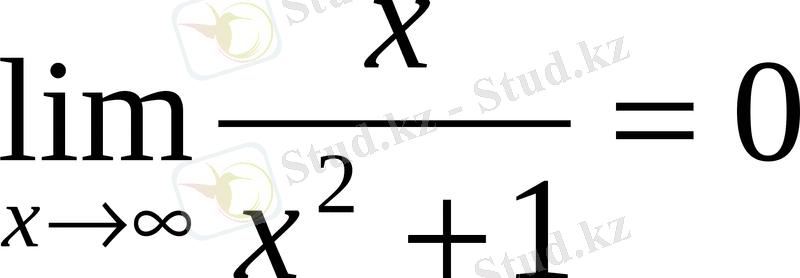Ескерту. Ақырсыз кіші шама әрқандай тұрақты кіші саннанда кіші болады.

Анықтама. Шегі $x \rightarrow x_{0}$ шексіздікке ұмтылғанда f(x) шексіз үлкен шама деп аталады. Немесе әрқандай үлкен санан да үлкен болған шамаға ақырсыз үлкен шама делінеді.

Мысал. ; ;

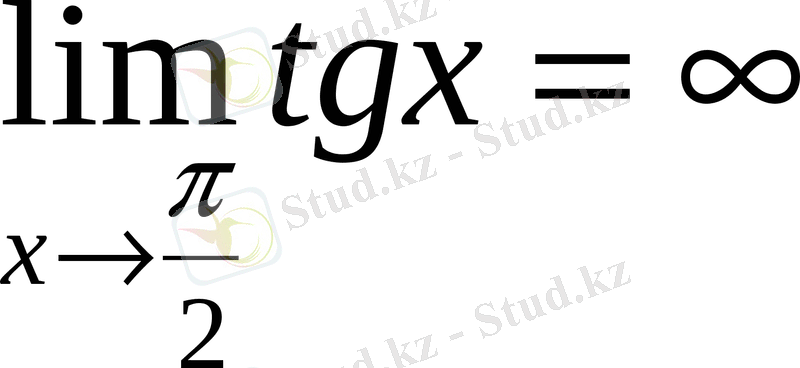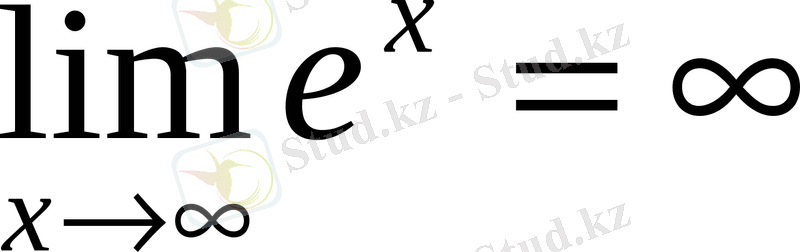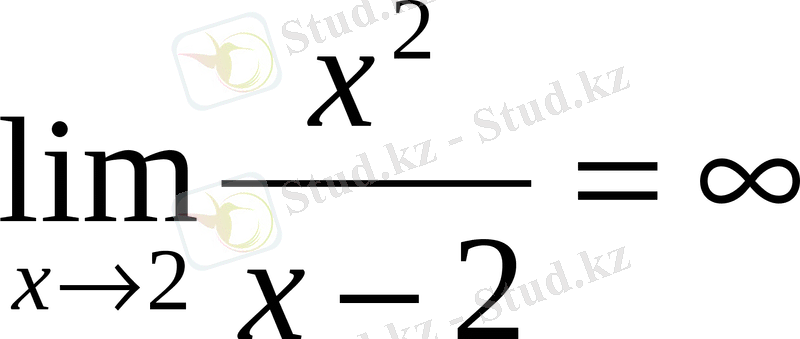
Ақырсыз кіші шамалардың негізгі қасиеттері туралы теоремалар:

1. Егер f(x) функцияның $x \rightarrow x_{0}$ ұмтылғандағы лимиті а-ға тең болып, f(x) шексіз кіші шама f(x) =a+a(x) болса онда теңдігі орындалады.

Мысал,

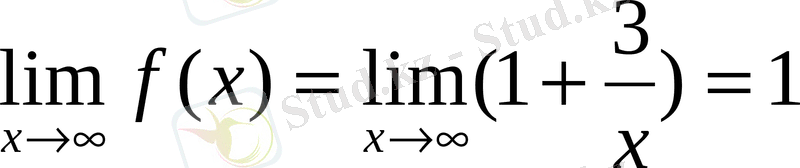
2) Егер d(x) шексіз кіші шама болса онда 1/d(x) шексіз үлкен d(x) =B(x) ақырсыз кіші шама

3) Егер ақырсыз кіші шаманың қосындысыда шексіз кіші шама болады шекті сандағы ақырсыз кіші шамалардың қосындысы шексіз кіші шама болады.

Монотонды тізбектер.

Анықтама. Егер әрбір n (n= 1, 2, . . . ) үшін $x_{n} < x_{n + 1}$ болса, онда {хn} тізбегін өспелі, ал егер болса, онда {хn} тізбегін кемімелі деп атайды.

Егер әрбір n (n=1, 2, . . . ) үшін $\ x_{n} \ll x_{n + 1}$ болса, онда {хn} тізбегін кемімейтін, ал егер $\ x_{n} \gg x_{n + 1}$ болса, онда {хn} тізбегін өспейтін тізбек деп атайды.

Бұл тізбектердің әрқайсысын монотонды деп атайды. Өспелі және кемімелі тізбектерді қатаң монотонды деп те атайды.

Кез келген жоғарыдан (төменнен) шенелген өспелі (кемімелі) тізбектің ақырлы шегі бар.

Монотонды және шенелген тізбектің әрқашанда нақты мәнді шегі бар болады, өйткені онда жиынының супремумы мен инфимумы нақты сан болады.

Қатаң монотонды тізбектердің монотонды тізбектерге қарағанда ерекше қасиеттері бар. Мәселен, монотонды тізбектің мәндерінің бәрі де шегіне тең болуы мүмкін (мысалы, xn ≡1 үшін), ал катаң монотонды тізбектің бірде-бір мәні шегіне тең бола алмайды.

Қорытынды

Шек - математиканың негізгі ұғымдарының бірі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.