Сандық жүйелер: санау жүйелері және логика алгебрасының негіздері


Кіріспе
Қазіргі кездегі мемелекетіміздің алдында тұрған ең негізгі мәселе - қоғамды ақпараттандыру. Бұл мәселені шешу үшін ақпаратты өндеу және беру жабдықтарын қарқынды дамыту қажет. Ақпаратты өндеу және беру процесін сандық сигналды пайдалана отырып іске асыру болады, себебі сандық беру тәсілінің бөгеу тұрақтылығы, дәлдігі жоғары, сонымен қатар басқарылуы қарапайым, автоматтандырылуы жеңіл, иілімділігі және беру сапасының арақашықтықта тәуелсізділігіжоғары.
Техниканың электроника, микроэлектроника саласы қазіргі уақытта ақпаратты жинау мен турлендіру, есептеуіш аппаратурасы, автоматты және автоматтандырылған басқару, энергияны шығару және түрлендіру облыстарындағы әр түрлі мәселелерді шешудегі әмбебап және өте тиімді құрал болып табылады.
Мәселен, өнеркәсіптегі көптеген технологиялық объектінібасқару жүйесі құрылымын қарайық. Бақыланатын шамалар(мысалы, температура, жылдамдық, қысым, т. б. ) туралы ақпарат бар электрлік сигналдар сәйкесті сезгіштер арқылы өнделіп шығарылады да, іріктеліп, сүзіліп және күшейтіліп, и арқылы цифрлық пішінге түрлендірілед. Сосын олар микропроцессорға беріледі. Микропроцессордың орнында компьютер болуы мүмкін. Микропроцессор қалыптастырған сигналдар цифрлі-аналогтық түрлендіргіштер көмегімен аналогтық турге айналдырылып, атқарушы механизидерді басқаратын, тікелей объектілерге әрекет ететін электрондық күштік құрылғыларға қозғалыштар, реттегіштер, т. б) беріледі қарастырылып отырған жүйе аналогтық (үздіксіз) сигналдармен (сүзгілер, күшейткіштер, күштік электрондық құрылғылар) және цифрлық сигналдармен (микропроцессор, компьютер) жұмыс істейтін электрондық құрылғылардан, сондай-ақ.
Сандық құрылғылар түсінігі қазір күнделікті өмірде жиі кездеседі; олар радиоқабылдағыштар, компьютерлер, теледидар, компьютерлер, олардың бәрі де микросхемалардан тұрады. Сандық құрылғылардын сипаттамалары оларды құратын элементтердің көрсеткіштерімен анықталады.
Электрониканың қазіргі кездегі рөлі микропроцессорлық техниканы, компьютерлік технологияны қолдануда, ақпараттықсигналдарды өндеуде жәнеэлектр энаргиясын түрлендіруге арналған күштік шалаөткізгіш аспаптарды пайдалануда өте күшейіп отыр.
1. 1 Санау жүйесіСимволдардың шектеулі жинақтау көмегімен сандар жазу ережелер жиынтығы санау жүйесі деп аталады. Санау жуйелері позиционды және позиционды емес болып болінеді. Позиционды емес жүйеге римдіктер санды белгілеу үшін қолданған жүйе мысал бола алады.
Позиционды санау жүйесінде қолданылатын символдар саны жүйе негізіне тең. Әр символдың салмағы (маңыздылығы) жүйе негізіне бөлінеді және жазылған санда берілген символдың алынатын позициясына тәуелді. Символ позициясының нөмірін разряд деп атайды.
Позиционды санау жүйесі түрлі арифметикалық операцияларды (қосу, азайту, көбейту, бөлу) орындауға ыңғайлы, сондықтан ол сандық және есептеу техникасында негіз болып табылады.
Жалпы жағдайда n-разрядті жағымды N саныпозиционды санау жүйесінде негізімен мына өрнекпен көрсетіледі.
 (1. 1)
(1. 1)
мұнда a k - қолданылатын жүйенің символдарының бірі, оның мәндері натурал қатарлы мүшелерге 0ден (р - 1) ге дейін диапазонда тең, р - санақ жүйесінің негізі, k - сандағы символ позициясының нөмірі, 0ден бастап, p k - салмақтық коэффициент.
Өндіріс электрониканың, микропроцессорлы техниканың және автоматиканың сандық құрылғыларында жиі позиционды санау жүйелерімен 2, 10, 16 негізінде жұмыс істейді.
Ақпаратты сандық және микропроцессорлі құрылғыларда өңдеу позиционды екілік санау жүйесінде (2 негізінде) жүргізіледі.
Екілік санды басқа санау жүйесінде көрсетілген сандардан айыру үшін, оны оң жақтан В (Binaire) жұрнағымен толықтырады, немесе 2 индексімен қамтамасыз етеді.
Екілік санды шағынырақ күйде көрсету үшін жиі оналтылық позиционды санау жүйесі қолданылады. Бұл жүйеде бірінші он натурал қатардағы 0ден 9ға дейін мүшелері, және бірінші алты латын әріптер Адан Fқа дейін (A = 10, B = 11, C = 12, D = 13, E = 14, F = 15) қолданылады. Оналтылық санды басқа санау жүйесінде көрсетілген сандардан айыру үшін, оны оң жақтан Н (Hexadecima) жұрнағымен толықтырады, немесе 16 индексімен қамтамасыз етеді.
Әртүрлі санақ жүйелерінің сандар сәйкестігі 1. 1 кестесінде көрсетілген.
1. 1 кесте - Әртүрлі санақ жүйелерінің сандар сәйкестігі
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
Позиционды санақ жүйелерінде толық сандарды жүйеден қандай да негізбен ондық жүйеге аудару (1. 1) формула бойынша орындалады. Мысалы 101011 2 екілік санын ондық санға түрлендіру 1. 1 формуласына формальді мән енгізгенде болады
Қандайда позиционды жүйеден сандарды ондық жүйеге аудару үшін “салмақты коэффициент” ұғымын қолдану ыңғайлы. (1. 1) формуласынан және де келтірілген мысалдан алғанда ондық эквивалентте өрнектелген екілік санның салмақ коэффициенттері 2 k - 1 …, 32, 16, 8, 4, 2, 1 сандар ретін көрсетеді.
Екілік санды ондыққа аударғанда, мәні 1-ге тең разрядтарда салмақтық коэффициент қалыптасады. Мысалы, 101011 2 екілік санын ондыққа аударғанда, екілік сандардың разрядтарына сай ондық салмақтық коэффициентін қойғанда мұндай нәтиже аламыз:
32 16 8 4 2 1
1 0 1 0 1 1
Бірлік 0, 1, 3, 5 разрядтарында болады (разрядтар санағы кішісінен, нөлден басталады), сондықтан 0, 1, 3, 5, немсе 1 + 2 + 8 + 32 = 43 разрядтарының салмақты коэффициенттері пайда болады.
Аударманы жеңілдету үшін жатқа 2 n n = 0ден n = 14ке дейінсандарының ондық мәндерін білу қажет. Бұл мәндер 1. 2 кестесінде көрсетілген.
1. 2 кесте - Екілік сан разрядтарының салмақтық коэффициенттері
Сандарды ондық жүйеден басқа позиционды жүйеге аудару ондық санды осы жүйенің негізіне келесіретті бөлу жолымен іске асырылады. Аударым нәтижесі бөлу процессінде алынған және ең соңғысынан бастап жазылған қалдықтар болады. Алынған санның үлкен разряды соңғы болү нәтижесі болады.
43 ондық санын екілікке аудару мысалы:
43 _2__
_42_ 21 _2__
1 _20 10 _2__
1 _10_ 5 _2__
0 _ 4_ 2 _2_
1 _2_ 1
0
Аударма нәтижесі: 43 10 = 101011 2
43 ондық санын оналтылыққа аудару мысалы:
43 _16_
_32_ 2
11
Аударма нәтижесі:43 10 = 2В 16 , өйткені 11 10 = В 16 ,
Он алтылық жүйе екілік сандарды кішігірім көрсетуге мүмкіндік береді. Он алтылық жүйеден екілік жүйеге (немесе керісінше) аударым ондық жүйеден екілікке аударғанға қарағанда оңай да тез.
Аударымда екілік санды кіші разрядтан бастап тетрадтарға (4 разрядтардан тұратын топтар) бөледі. Үлкен топты керегінше екілік сан алдына нөл жазып тетрадаға дейін толтырады. Алынған тетрадаларды он алтылық сандарының разрядтарын көрсетеді, сондықтан аударымда екілік тетрада он алтылық санымен ауыстырылады ( 2 0 16ға сай, … 2 F 16ға сай) . Екілік тетрадалармен он алтылық сандардың сәйкестігі 1. 1 кестесінде көрсетілген.
Екілік санды он алтылыққа аудару мысалы:
101011 2 = 0010 1011 2 = 2В 16.
2 16 В 16 .
өйткені 0010 2 = 2 16 , ал 1011 2 = В 16 .
Қайта өту аналогті түрде іске асады - он алтылық санның әр бір разряды оған эквивалентті екілік тетрадамен ауыстырылады.
Позиционды санау жүйелерімен қатар өндіріс электрониканың, микропроцессорлі техниканың, және автоматиканың сандық құрылғыларында позиционды емес жүйемен кодтар қолданылады. Жиі екілі- ондық және унитарлы жүйе көп қолданылады.
Екілі-ондық санау жүйесінде сан төрт разрядты екілік комбинацияның (тетрадалардың) келесіретін көрсетеді, оның саны эквивалентті ондық санының разряд санына тең. Әрбір екілік тетрада ондық санының бір разрядыныңекілік эквиваленті болып табылады. Екілік тетрада мен ондық сандардың сәйкестігі 1. 1 кестесінде көрсетілген. Тетраданың сандық мәні 9дан (ондық эквивалентте) көп бола алмайтынын айта кету керек. Егер екілі- ондық санды тетрадалар арасында қалдырады, ал толмаған үлкен тетраданы нөлдермен толтырады.
Екілі-ондық санды басқа санау жүйедегі саннан айыру үшін оны оң жағынан BD (Binary Decimals) жұрнағымен толықтырады, немесе 2-10 индексімен қамтамасыз етеді.
Екілік санды ондыққа аудару мысалы:
101001 2-10 = 0010 1001 2-10 = 29 10
2 10 9 10 .
өйткені 0010 2 = 2 10 , а 1001 2 = 9 10 .
Қайта өту аналогті түрде іске асады - ондық санның әр бір разряды оған эквивалентті екілік тетрадамен ауыстырылады.
Унитарлы жүйеде 1символы үнемі тек бір позицияда болады, ал қалған позицияларда 0 болады. 1 саны бар позиция нөмері (0ден бастап унитарлы санының ондық эквиваленті болып табылады. Нөлінші нөмір оң жақтағы шеткі.
Унитарлы (сегіз разряд үшін) және ондық санау жүйелерінің сан сәйкестігі 1. 3кестесінде көрсетілген.
1. 3 кесте - Унитарлы және ондық санау жүйелерінің сан сәйкестігі
0
1
2
3
4
5
6
7
1
10
100
1000
0001
001
01
1
Сандық құрылғылардың іс әрекетін бейнелейтін математикалық аппарат логика алгебрасында немесе оның басқа атауы ағылшын математигі Джордж Булдің атында бульді алгебра деп атайды.
Математикалық логиканың негізін салған неміс математигі Готфрид Вильгельм Лейбниц (1646 - 1716 жж. ) . Ол универсалды тіл салуға қадам жасаған, соның көмегімен адамдар арасындағы бәсекелесті есеппен шешуге болушы еді. Лейбниц салған негізде ирлан математигі Джордж Буль (1815-1864 жж. ) математикалық логиканың- жаңа ғылым мекемесін салған, ол жай алгебрадан айырмашылығы санмен емес сараптамамен оперирлейді.
Сараптама - бұл қандайда бір тұжырым, соған қатыст немесе жалған, сондай-ақ шындыққа сай ма екенін айтуға болады.
Осымен, сараптама бойынша екілік объект болып табылады, сондықтан сараптаманың шындық мәніне - 1-ге сай, ал жалған мәніне - 0 қояды.
Сараптамалар жай және күрделі болады. Жай сараптамалар алгебраикалық айнымалыларға сай, ал күрделілер алгебраикалық функцияның аналогы болып табылады. Функцияларды айнымалыларды қосу жолымен логикалық іс әрекет көмегімен алуға болады.
Техникалық жүйелерді анализдеу үшінлогика алгебрасын қолдануды көсеткен П. С. Эренфест (1910 ж. ), ал 1938 ж. К. Шеннон Буль алгебрасын релелі сұлбаларын есептеуге қолданған. Осы уақытта логика алгебрасының математикалық аппарат сандық құрылғыларды жобалаудың негізі болып табылады.
Логика алгебрасы екілік айнымалымен оперирлейді, олар шартты белгіленеді, 0 және 1 сияқты. Айнымалыларды белгілеу үшін латын алфавитінің әріптері қолданылады. Алдымызда айнымалыларды белгілеу үшін Х әрпі индексімен, 1ден бастап айнымалының белгіленген нөмірі қолданылады. Функция үшін f (ν) мәні алынған, мұнда ν = (Х n , …, Х 1 ) айнымалылар жиынтығы. Айнымалылар шексіз көп болуы мүмкін, бірақ айнымалы комбинациялар саныжиынтықта үнемі 2 n ге тең
n айнымалыларының функциялары жиын айнымалыларының (Х n , …, Х 1 ) бәріне тәуелді емес, оларды туынды деп атайды. Барлық айнымалылар жиын (Х n , …, Х 1 ) комбинациялары мәні берілген n айнымалыларының функциясытолық анықталған деп аталады. Егер де бір айнымалы жиынының е функция мәні берілмесе, онда ол толық анықталмаған функция болып табылады. Толық анықталмаған функцияны керегінше анықтап, бұл жағдайда оған керек мән беру қажет.
1. 3 Логика алгебрасының тепе теңдігімен теоремаларыЛогика алгебрасының тепе теңдігі мен теоремалары функция өрнегін жеңілдету үшін қолданылады. Тепе теңдік теоремаларды дәлелдегенде қолданылады. Теоремалармен тепе теңдіктер логика алгебрасында оның аксиомаларын қолданылуымен айнымалылардың барлық мәндерін жинау әдісімен дәлелденеді.
1. 4 Логикалық функцияларды тапсырма ретінде беру тәсілдеріВ Логика алгебрасында жақша өрнегінде жоқ болса келесі ретті әрекеттер енгізіледі: бірінші болып терістеу операциялары орындалады, соңынан - конъюнкцияның, кейін - дизъюнкция орындалады. Бар болса бірінші жақша ішіндегі операциялар орындалуы тиіс.
Тепе теңдікті қолданамыз
Х 3 ∙ 1 ∨ Х 3 ∙Х 2 ∨ Х 2 ∙Х 1 . Жақша сыртына қайта шығарамыз Х 3 . Х 3 (1 ∨ Х 2 ) ∨ Х 2 ∙Х 1 . Тепе теңдікті қайта қолданамыз
. Х 3 ∙ 1 ∨ Х 2 ∙Х 1 . Тепе теңдікті қайта қолданамыз
. Х 3 ∨ Х 2 ∙Х 1 . Алынған өрнек шығысты қатынастың сол жағымен сәйкес келеді. Сонымен, дистрибутивті заңның шындығы дәлелденді.
Логика алгебрасында негізгі орынды Шеннон құрған екіліктің заңы алады. Бұл заң әрбір функцияның инверсиясын анықтайды және мұндай түрде беріледі:
,
мұнда
,
. Сонымен, егер функциядағы өрнекте
айнымалысын оның
инверсиясымен ауыстырса және керісіншеде, дизъюнкциямен конъюнкция операцияларын қарым-қатынаста ауыстырса әрбір функцияның инверсиясын алуға болады. Мысалға, егер
онда

Тәжірибеде қолданғанда екілік заңының жеке жағдайы болады - де Морган теоремасы:


Немесе тәжірибеде қолдануға ыңғайлырақ түрде
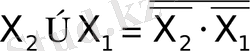
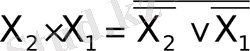
де Морган теоремасы тәжірибеде берілген базиске функцияны аудару үшін, сондай-ақ керек жағдайда дизъюнкция операциясын конъюнкцияға немесе керісінше ауыстыруға қолданылады. Мысалы
өрнегінің құрамында тек дизъюнкция операциялары болуы керек. де Морган ережесін қолданған соң
шығады. де Морган теоремасын айнымалылардың үлкен санына да таратуға болады.
Логикалық функцияларды әр түрлі тәсілдермен беруге болады: ауызша, ақиқат кестесімен, аналитикалық өрнекпен, шартты графикалық белгілер қолдана отырып. Әрбір нақты жағдайда ең ыңғайлы тәсіл қолданады.
Логикалық функцияны базалық тәсілмен беру ақиқат кестесі болып табылады. Ақиқат кестесінде айнымалы мәндерінің комбинациялары және оларға сай функция мәндері беріледі.
Ақиқат кестесі өзіне жолақ нөмірімен бір қатар қосады (ол міндетті түрде қажет емес, болмауыда болады), қатарлар айнымалылармен (олардың саны айнымалылардың санына тең), қатарлар функциялармен (олардың саны логикалық функциялардың шығысына тең) . Толық ақиқат кестесінің құрамында 2 n жолақтары болады, мұнда n айнымалылар саны. Ақиқат кестесінде жолақтар нөлден бастап нөмірленеді.
Айнымалылар комбинацияларын ақиқат кестесінде қалаған ретте орналастыруға болады, бірақ келесі жүйеге сүйенген жөн. Үлкен айнымалы үлкен индекспен белгіленіп, сол жақ шеткі қатарда орналасады, қалғандары үлкеннен бастап азаю ретімен орналасады. Айнымалы мәндерінің комбинациясы жолақта екілік кодта жол нөмірін өрнектеу керек. Кестеде жолақтар монотонды өсу ретімен орналастырады, нөлден бастап. Мұндай ережелер ақиқат кестесін қатесіз толтырып және онымен жұмыс істеуді жеңілдетеді. Осы ережелермен толтырылған үш айнымалы үшін произволды функцияның ақиқат кестесі 1. 1суретінде көсетілген.
1. 1сурет Үш айнымалы үшін ақиқат кестесі
Келтірілген кесте бойынша жай, жылдам қатесіз айнымалылардың мәндерімен толтыру: бірінші қатарда айнымалылар бірден кейін кезектесіп отырады (0-1-0-1 т. с. с. ), екінші қатарда екі реттен кейін (00-11-00 т. с. с. ), үшіншіде төрттен кейін (-- т. с. с. ), төртіншіде сегізден кейін кезектесіп отырады. Келесі үлкен айнымалыға кезектесу дәрежесі екі еселенеді.
Функцияны сөзбен бейнелеуде қандай жағдайда функция 1- ге тең болғанын өрнектеу керек.
2. Қарапайым логикалық функцияларБір немесе екі айнымалылардың функцияларын қарапайым логикалық функциясы деп атайды. Функцияның әр түрлі мәндерінің саны 2 m ге тең, мұнда m 2 n ге тең (n -айнымалылар саны) . Сонымен, бір айнымалы үшін функция саны- 4, ал екі айнымалы үшін - 16. Олардың бәрінде атауы бар және 1. 4 пен 1. 5 кестесінде көрсетілген.
1. 4 кесте - Бір айнымалының функциялары
1. 5 кесте - Екі айнымалының функциялары
 Х
2
Х
1
Х
2
Х
1
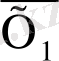
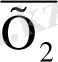
Тәжірибеде бір немесе екі айнымалы функцияларының бәрі қолданылмайды. Күрделі сызбаны іске асыру үшін бір екеуі ғана жеткілікті.
Одан басқа, бір функцияларды басқа функция арқылы тепе- теңдік және логика алгебрасының теорема ережелерін қолданып өрнектеуге болады. Интегралды орындауда іске асырылған және микропроцессормен микроконтроллерді бағдарламалау тілінде бар қарапайым функцияларды қарастырайық.
Терістеу ( инверсия, НЕ функциясы) . Айнымалылардың үстіне сызықша белгіленеді. Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 1. 2 суретінде көрсетілген.
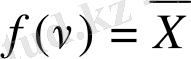
1. 2 сурет
Сөзбен бейнелеу: функция инверсті (қарама- қарсы) айнымалы мәнін қабылдайды.
Конъюнкция ( логикалық көбейту, И функциясы) . Айнымалылар арасында ∙ символымен белгіленеді ( сондай да & және ∧ символдары қолданылады ) . Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 1. 3 суретінде көрсетілген.
f (ν) = Х 2 ∙ Х 1
Сөзбен бейнелеу: функция бірлік мәнді егер барлық айнымалылар бірге тең болса қабылдайды.
Дизъюнкция ( логикалық қосу, ИЛИ функциясы) . Айнымалылар арасында ∨ символымен белгіленеді ( сондай да + символы қолданылады) . Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 1. 4суретінде көрсетілген.
f (ν) = Х 2 ∨ Х 1
1. 4 сурет
Сөзбен бейнелеу: функция бірлік мәнді бір айнымалы бірге тең болса қабылдайды.
Конъюнкция терістеумен ( логикалық көбейту терістеумен, И- НЕ функциясы Айнымалылар арасында ∙ символымен белгіленеді, өрнек үстіне сызықша қойылады (сондай да & және ∧ символдары қолданылады Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 1. 5 суретінде көрсетілген
f (ν) = Х 2 ∙ Х 1
Сөзбен бейнелеу: функция бірлік мәнді, егер бір айнымалы нөлге тең болса қабылдайды.
Дизъюнкция терістеумен (логикалық қосу терістеумен, ИЛИ-НЕ функциясы) . Айнымалылар арасында ∨ символымен белгіленеді, өрнек үстіне сызықша қойылады ( сондай да + символы қолданылады) . Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 1. 6 суретінде көрсетілген.
f (ν) = Х 2 ∨ Х 1
Сөзбен бейнелеу: функция бірлік мәнді тек барлық айнымалылар нқлге тең болғанда қабылдайды.
Теңсіздік ( исключающее ИЛИ ) . Айнымалылар арасында ⊕ символымен белгіленеді. Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 1. 7 суретінде көрсетілген.
f (ν) = Х 2 ⊕ Х
1. 7 сурет
Сөзбен бейнелеу: функция бірлік мәнді тек бір айнымалы бірге тең болғанда қабылдайды. Екі айнымалы үшін (бірақ екеуі үшін) осы функция модуль бойынша сомма екі математикалық операциясын көрсетеді.
2. 1 Логикалық функцияларды таныстыру тәсілдеріФункцияның аналитикалық өрнегін ақиқат кестесінен құрауға болады. Осы процессті формальдау үшін кейбір ұғымдарды енгізү керек.
Элементар (қарапайым) конъюнкция ондағы әрбір терістеумен айнымалы немесе терістеусіз бірден көп емес кезігетін болып табылады. Айнымалылар тобының терістеуі болмайды.
Мысалы:
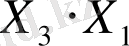 ,
,
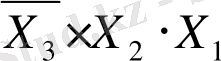 ,
,
Элементар (қарапайым) дизъюнкция ондағы әрбір терістеумен айнымалы немесе терістеусіз бірден көп емес кезігетін болып табылады. Айнымалылар тобының терістеуі болмайды.
Минтерм 1-ге тең тек айнымалылардың бір комбинациялары үшін.
Минтерм К i символымен белгіленеді, мұндағы i - индекс, ол бірмәнде минтермнің (конъюнкциямен) аналитикалық өрнегімен тепе- тең болады. Минтерм индексін біле отырып, оның аналитикалық өрнегін анықтауға немесе керісінше болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz