Интеграл ұғымының тарихы мен оқыту әдістемесі: алғашқы функция, анықталған интеграл және қолданылуы


Жоспар
Кіріспе
1. Математика тарихындағы интегралдың қалыптасуы.
2. Алғашқы функция ұғымы мен анықтаманың енгізілуі.
2. 1 Қисық сызықты трапецияның ауданы және интеграл.
3. Дененің көлемін есетеуге интегралдың қолданылуы.
Қорытынды
Кіріспе
Алгебра және анализ бастамалары курсындағы шек және туындыны есептеу әдістері мен туындыны қолдану ұғымымен танысқаннан кейін, оқушылар интеграл ұғымы мен интегралды есептеу әдістерімен танысады. «Интеграл» тақырыбында алғашқы функция және оның қасиеттері, интеграл дың негізгі теоремасы, интегралды табудың ережелері, дененің ауданы мен көлемін табуға интегралды қолдану сұрақтары қарастырылады.
Оқу құралдарында және әдістемелік әдебиеттерінде интегралды есептеу әртүрлі тәсілде баяндалған.
Кей оқу құралдарында анықталған интегралды енгізу мен оқыту туындыны қолданумен байланыспайды. Көбінесе анықталған интегралды енгізер алдында туынды ұғымы беріледі. Сондықтан авторлар алғашқы функция мен анықталған интегралды оқыту тәсілін әр түрлі таңдайды: не алдымен анықталған интегралдың анықтамасы беріледі де, оқушылар жеткілікті мөлшерде Ньютон- лецбниц формуласын жетік игергеннен кейін, алғашқы функция ұғымы беріледі; не бірінші алғашқы функция ұғымы беріледі де, содан кейін интеграл ұғымы енгізіледі. Сонымен қатар анықтамалар да әртүрлі беріледі. Классикалық математикалық анализде анықталған интеграл интеграл қосындысының шегі арқалы берілсе, мектепке арнылған А. Н. Колмогоровтың редакциясын басқарған оқулықта интеграл алғашқы функция өсімшесі ретінде енгізілген.
Анықталған интеграл:
- алғашқы функция өсімшесі (бағдарламаның талабы бойынша)
- интеграл қосындысының шегі ( жоғары оқу орындарындағыдай)
ретінде енгізу тәсілі - басты методикалық мәселе болып табылады.
Оқушылардың интегралды есептеу элементтерін жақсы менгерілуі осы мәселенің шешімінен байланысты. Бұл тәсілдердің әрқайсысының кемшіліктері мен артықшылықтары бар.
Егер интеграл қосындысының шегі түрінде енгізетін болсақ, онда интегралды оқыту процесі көп уақыт талап етеді. Сонымен қатар Ньютон - Лейбниц теоремасын қарастыру керек болады. Тек анықтамаға сүйеніп интегралды интеграл қосындысының шегі ретінде есептеу және теорияны құру оңай емес. Егер алғашқы функцияның өсімшесі ретінде анықталған интеграл ұғымын енгізетін болсақ, онда бұл тәсілдің берілуі қысқа және Ньютон-Лейбниц формуласының қорытындысын талап етпейді. Анықталған интегралды алғашқы функция өсімшесі ретінде енгізетін болсақ, онда интегралдық есептеулер бөлімінің теориясын құру оны әрі қарапайым, әрі қолайлы баяндауға мүмкіндік береді. Бұл тәсілдің негізгі артықшылығы осында.
1. Математика тарихындағы интегралдың қалыптасуы.
Интеграл ұғымының тарихы квадратуларды табу есептерімен тығыз байланысты. Қандай да болмасын жазық фигураның квадратурасы туралы есептер деп Ежелгі Греция мен Римнің математиктері қазір өзіміз аудандарды есептеп шығаруға берілген есептерге жатқызып жүрген есентерді айтқан болатын. Латын сөзі guadratura деген квадрат пішінге келтіру деп аударылды.
Мына ∫ символды Лейбниц (1675ж. ) енгізген. Бұл таңба латынның S әрпінің (summa сөзінің бірінші әрпі ) өзгерген түрі. Интеграл деген сөздің өзін Я. Бернулли (1690ж. ) ойлап шығарған . Шамасы оның шығу тегі латынның integro сөзіне саятын болар, оның мағынасы: бұрынғы қалпына түсіру, орнына келтіру. Шынында да, интеграл астындағы функция шығарып алатын дифференциялдау арқылы интегралдау амалы функцияны қалпына келтіреді. Интеграл терминінің шығу тегі өзге болуы да мүмкін: integer деген бүтін дегенді білдіреді.
1696ж математиканың жаңа тармағының атауы - интегралдық есептеу пайда болды, мұны И. Бернулли енгізді. Интегралдық есептеуге қатысты басқа терминдер біршама кейін пайда болды. Қазір қолданып жүрген алғашқы функция атауы қарапайым функция орнын басты, мұны енгізген Лагранж (1797ж. ) Латынның сөзі primitivus «бастапқы» деп аударылды: F(x) =∫ f(x) dx-f(x) үшін бастапқы (немесе алғашқы), бұл F(x) -ті дифференциалдаудан шығады.
Қазіргі әдебиетте f(x) функциясы үшін барлық алғашқы функциялардың жиыны, сондай-ақ анықталмаған интеграл деп аталады. Бұл ұғымды айырып кһрсеткен Лейбниц еді, ол барлық алғашқы функциялардың бір-бірінен айырмашылығы алынатын тұрақты сан екенін аңғарған болатын. Ал
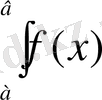 dx анықталған интеграл деп аталады. (белгілеулерді енгізген К. Фурье, бірақ интегралдар шектерін Эйлер көрсеткен) .
dx анықталған интеграл деп аталады. (белгілеулерді енгізген К. Фурье, бірақ интегралдар шектерін Эйлер көрсеткен) .
Ескі грек математиктерінің жазық фигуралардың квадратурасын табу (яғни аудандарды есептеу), сондай-ақ денелердің кубатурасын табу (көлемдерін есептеу) есептерін шығарғандағы тауысу әдісімен байланысты, мұны ұсынған Книдский Евдокс. Оның әдісін жетілдірген Архимед болды . Интегралдық есептеу жөнінен көптеген идеяларды болжап білген.
17ғ-да интегралдық есептеулерге қатысты көптеген жаңалықтар ашылған болатын . Мәселен, П. Ферма сол 1629ж кез келген қисықтың у=x
n
, n-бүтін сан, квадратурасын шешкен болатын (яғни негізінен
 x
n
dx =
x
n
dx =
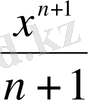 формуласын қорытып шығарады.
формуласын қорытып шығарады.
Көптеген дербес есептердің шешімі негізделетін жалпылама идеяларды, сондай-ақ дифференциялдау мен интегралдау амалдарының арасындағы байланыстарды тағайындау қажет болды. Мұны орындаған Ньютон-Лейбниц формуласы деп аталып жүр. Ендігі орындалатын - көптеген функциялардың алғашқы функцияларын табуды үйретіп, жаңаша есептеудің логикалық негіздемесін т. б. бере білуді үйрену еді, ең негізгісі орындалды да, дифференциалдық және интегралдық есептеу құрылды.
2. Алғашқы функция ұғымы мен анықтаманың енгізілуі.
А. Н. Колмогоровтың «Алгебра және анализ бастамалары » оқн құралының алғашқы басылымдарында мынадай тәсілде баяндалған. Алдымен алғащқы функция ұғымы енгізіледі де, содан кейін интеграл беріледі. Мектеп бағдарламасына енетін алғашқы функция ұғымын оқыту дифференцмалды есептеумен байланысты.
Алғашқы функция ұғымын енгізу үшін функция және оның туындысы жазылған кестеге назар аударуға болады.
1. у=C (C-тұрақты) у ′=0
2. y=x y′=1
3. y=x k (k-бүтін сан) y′=kx k-1
4. y=x 2 y′=2x
5. y=x 3 y′=3x -3
6. y=x -2 y′=-2x
7. y=x -3 y′=-3x -4
8. y=sinx y′=cosx
9. y=cosx y′=-sinx
Туындылары х 2 , х 3 , х -2 , х -3 болатын функцияны табу - бұл есептің әрі қарай дамуы. Берілген есеп бір мәнді есептелмейді: туындысы берілген функцияға тең болатын әр функция үшін шексіз функция жиыны табылады. Бұл функциялар тұрақтысымен ғана ерекшеленеді. Мысалы, 2х
у=х 2 функциясының туындысы у=х 2 +0, 5 функциясының туындысы да болып табылады. Жалпы алғанда, кез келген функцияның туындысы у=х 2 +С, мұндағы С-тұрақты.
Осындай жаттығулардан кейін алғашқы функция анықтамасы беріледі.
Бізге берілген кестеден алғашқы функциясын тауып алуға ыңғайлы етіп, мынадай түрде жазып алуға болады.
1. f(x) =0 F(x) +C ( C-тұрақты )
2. f(x) =1 F(x) =x+C
3. f(x) =2x F(x) =x 2 +C
4. f(x) =3x 2 F(x) =x 3 +C
5. f(x) =-2x -3 , x≠0 F(x) =x -2 +C
Ары қарай теоремалар дәлелденеді.
Теорема: Қандай да бір аралықта (шексіз немесе шексіз емес) f(x) функциясы үшін алғашқы функциялардың кез келгенін мына
F(x) +C
түрінде жазып көрсетуге болады, мұндағы С- кез келген тұрақты шама, ал F(x) - қандай да бір аралықтағы f(x) функция үшін алғашқы Функциялардың бірі.
Теорема: Егер F(x) функциясы f(x) үшін алғашқы функция болса, онда f(x) үшін кез келген басқа алғашқы функцияны
F(x) +C
түрінде көрсетуге болады, мұндағы С- қандай да бір тұрақты.
Сонымен, F(x) +C -өрнегі берілген функцияның барлық алғашқы функция жиынын көрсетеді.
Осы теоремалардың дәлелдемелерінен кейін физикалық мазмұнды және басқа есептер шығарады. Мысалы: уақытты функция ретінде дене жылдамдығы v=at (а-үдеу) формуламен берілген жолды уақыт қозғалысының функциясы ретінде табыңдар.
Осындай түрдегі есептер алғашқы функция ұғымын енгізу үшін ізашар бола алады.
А. Н. Колмогоровтың соңғы басылымдағы 10-11сыныпқа арналған оқү құралында бірінші алғашқы функция анықталғаннан кейін, интеграл ұғымы беріледі Механикадан дифференциалдау амалына кері интегралдау амалын қолданып шығаратын мысал келтіріледі. Мысалда мынадай есеп қарастырылады.
Егер бастапқы t=0 уақыт мезетінде дененің жылдамдығы 0-ге тең болса, онда еркін түсетін дене t уақыт мезетінде мынадай жол жүреді:
s(t) =
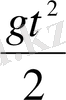
Дифференциалдау арқылы жылдамдықты табамыз:
s′(t) =v(t) =gt
Екінші рет дифференциалдасақ, үдеу табылады:
v′(t) =a(t) =g
яғни үдеу тұрақты.
Осы мысалдан кейін алғашқы функция анықтамасы беріледі.
Анықтама: Егер берілген аралықтағы барлық х үшін
F′(x) = f(x) (1)
болса, онда осы аралықта F функциясын f функция үшін алғашқы функция деп атайды.
Осы анықтамадан кейін алғашқы функцияға қатысты мысалдар қарастырылған.
1-мысал. F(x) =
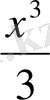 функциясы f(x) =x
2
функция үшін (-∞; ∞) интервалында алғашқы функция болады, өйткені барлық х
функциясы f(x) =x
2
функция үшін (-∞; ∞) интервалында алғашқы функция болады, өйткені барлық х
 (-∞; ∞) үшін
(-∞; ∞) үшін
F'(x) =
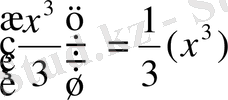 '
=
'
=
 ∙3x
2
=x
2
=f(x) .
∙3x
2
=x
2
=f(x) .
Ал
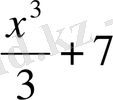 функциясының туындысы да сол х
2
болатынын байқау қиын емес, сондықтан
функциясының туындысы да сол х
2
болатынын байқау қиын емес, сондықтан
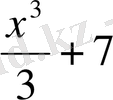 функциясы да х
2
үшін R жиынында алғашқы функция бола алады.
функциясы да х
2
үшін R жиынында алғашқы функция бола алады.
Алғашқы кездерде алғашқы функция ұғымын бекіту үшін және қате болу мүмкіндігін жою үшін дифференциалдаумен шығарылған есептердің дұрыстығын тексеру қажет. Алғашқы кездерде оқушылар дифференциалдау мен интегралдау формулаларын шатастыруы мүмкін.
Ары қарай алғашқы функцияның негізгі қасиеті беріледі.
Теорема: I аралығында f(x) функциясы үшін алғашқы функциялардың кез келгенін мына түрде
F(x) +C (2)
жазып көрсетуге болады, мұндағы С- кез келген тұрақты шама, ал F(x) -I аралығында f(x) функция үшін алғашқы функциялардың бірі.
Бұл пікір алғашқы функцияның екі қасиетін қысқаша тұжырымдап отыр:
- сол (2) өрнектің орнына қандай санды қойсақ та, I аралығында f үшін алғашқы функция шығады;
- I аралығында f үшін қандай алғашқы функция Ф-ті алсақ та, I аралығындағы барлық х үшін
Ф(х) =F(x) +C
теңдігі орындалатындай, бір С санын таңдап алуға болады.
Дәләлдеу. 1) Шарт бойынша F функциясы f үшін I аралығында алғашқы функцич. Олай болса, кез келген х
 I үшін F'(x) =f(x)
I үшін F'(x) =f(x)
Сондықтан
(F(x) +C) '=F'(x) +C'=f(x) +0=f(x)
яғни F(x) +C функциясы -f(x) функциясы үшін алғашқы фугкция
2) Айталық, Ф(х) функциясы f функция үшін сол I аралығында алғашқы функциялардың бірі болсын, яғни барлық х
 I үшін Ф'(х) =f(x) болсын
I үшін Ф'(х) =f(x) болсын
Сонда
(Ф(х) -F(x) ) '= Ф'(х) -F'(x) =f(x) -f(x) =0
Бұдан функцияның тұрақтылық белгісі бойынша Ф(х) -F(x) айырымы I аралығында қандай да бір тұрақты С шамасын қабылдайтын функция екені шығады.
Теореманың делелдемесі беріледі және алғашқы функцияның негізгі қасиетін геометриялық мағанада береді. Осыдан кейін алғашқы функцияларды табу мысалдары қарастырылады.
1-мысал. f(x) =-x 3 функциясы үшін R жиынында алғашқы функциялардың жалпы түрін табайық.
f функциясы үшін алғащқы функциялардың бірі -
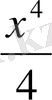 функциясы екенін көреміз, өйткені
функциясы екенін көреміз, өйткені
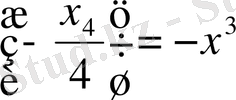 . Жоғарыда дәлелденген теорема бойынша f функция үшін алғашқы функциялардың жалы түрі мынадай:
. Жоғарыда дәлелденген теорема бойынша f функция үшін алғашқы функциялардың жалы түрі мынадай:
F(x) =-
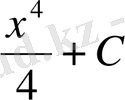
2-мысал: f(x) =
 функция үшін (0; ∞) аралықта х=1 болғанда 1-ге тең мәнді қабылдайды, алғашқы F
0
(x) функциясын табайық.
функция үшін (0; ∞) аралықта х=1 болғанда 1-ге тең мәнді қабылдайды, алғашқы F
0
(x) функциясын табайық.
f функциясы үшін алғашқы фунуцияның түрі F(x) =-
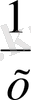 +C болады. Шарт бойынша F(1) =1 болғандықтан, мына түрдегі -1+С=1 теңдеуге (С-ға қатысты) келеміз, бұдан С=2, олай болса, F
0
(x) =-
+C болады. Шарт бойынша F(1) =1 болғандықтан, мына түрдегі -1+С=1 теңдеуге (С-ға қатысты) келеміз, бұдан С=2, олай болса, F
0
(x) =-
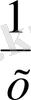 +2.
+2.
Мысалдардан кейін алғашқы функцияларды табудың үш ережесі беріледі. Бұл ережелер дифференциалдаудың сәйкес ережелеріне ұқсас.
1-ереже. (F+G) ′= F′+G′= f+g
2-ереже. (kF) ′= kF′=kf (k- тұрақты шама)
3-ереже. (
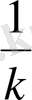 F(kx+b) ) ′=
F(kx+b) ) ′=
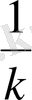 F′(kx+b) ∙k=f(kx+b) (k мен b-тұрақты шамалар)
F′(kx+b) ∙k=f(kx+b) (k мен b-тұрақты шамалар)
Ережелер берілгеннен кейін, осы ережелерді пайдаланатын мысалдар келтіріледі.
1-мысал. f (x) =x
3
+
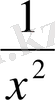 функциясы үшін алғашқы функцияның жалпы түгін табайық.
функциясы үшін алғашқы функцияның жалпы түгін табайық.
Х
3
функциясы үшін алғашқы функциялардың бірі
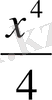 , ал
, ал
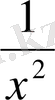 функциясы үшін алғашқы функциялардың бірі -
функциясы үшін алғашқы функциялардың бірі -
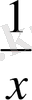 болатындықтан, 1-ші ереже бойынша :f(x) =x
3
-
болатындықтан, 1-ші ереже бойынша :f(x) =x
3
-
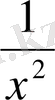 функциясы үшін алғашқы функциялардың бірі
функциясы үшін алғашқы функциялардың бірі
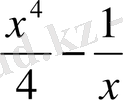 болады.
болады.
2. 1 Қисық сызықты трапецияның ауданы және интеграл.
Алдын-ала оқушыларда Ох осінің [a; b] кесіндісінде үздіксіз әрі осы кесіндіде таңбасы өзгермейтін f функция графигімен, [а; b] кесіндісімен және x=a, x=b түзулерімен шектелген фигураны қисық сызықты трапеция екені жөнінде дұрыс түсінік қалыптасуы керек. (1-сурет)
Қисық сызықты трапециялардың аудандарын есептегенде мыныдай теореманы пайдаланады.
Теорема: Егер f - [a; b] кесіндісінде үздіксіз және теріс емес функция да, ал F-оның осы кесіндідегі алғашқы функциясы болса, онда сәйкес қисық сызықтың трапецияның(2-сурет) S ауданы [a; b] кесіндідегі алғашқы функция өсімшесіне тең болады, яғни
S=F(b) -F(a) (3)
Дәлелдеу. [a; b] кесіндісінде анықталған S(x) функциясын қарастырайық. Егер а<х≤b болса, онда S(x) - M(x; 0) нүктесі арқылы өтетін вертикаль түзудің сол жағын ала орналасқан қисық сызықты трапеция бөлігінің ауданы (2, а-сурет) . Егер х=a болса, онда S(a) =0 болады. Енді S(b) =S екенін ескереміз. (S-қисық сызықты трапецияның ауданы) .
Сонда S′(x) =f(x) (4)
Болатынын дәлелдейік. Туындының анықтамасы бойынша мынаны дәлелдеу керек: ∆х→0 жағдайда
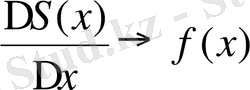
∆S(x) алымының геометриялық мағынасын анықтайық. Жеңілдік үшін ∆х>0 жағдайды қарастырамыз. ∆S(x) = S(x+∆x) -S(x) болатындықтан, ∆S-2, ә-суреттегі штрихталған фигураның ауданы. Енді [х; ∆х] кесіндісіне тіреліп жатқан ауданы сондай ∆S(x) болатын тік төртбұрышты алайық. (2, б-сурет) .
Осы тік төртбұрыштың жоғары қабырғасы функцияның графигін абсциссасы ( ол үздіксіз болатын себебі) с [x; x+∆x] , болатын қандай да бір нүктеде қиып өтеді ( өтпегенде ол тік төртбұрыш қисық сызықты трапецияның [x; x+∆x] кесіндісі шектеген бөлігіне қамтылады, не болмаса оны қамтиды; соған сәйкес оның аудпны ∆S(x) -тен не артық, не кем болады) . Тік төртбұрыштың биіктігі f(c) -ке тең. Тік төртбұрыш ауданының формуласы бойынша мынау шығады: ∆S(x) =f(c) ∆x, бұдан
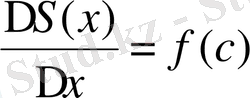 . (Бұл формула ∆х<0 болғанда да тура. Ал с нүктесі х пен х+∆х аралығында жататын себебі, ∆х→0 жағдайда с нүктесі х-ке ұмтылады) . f Функциясы үздіксіз болғандықтан, ∆х→0 жағдайда f(c) →f(x) . Cонымен, ∆х→0 болғанда
. (Бұл формула ∆х<0 болғанда да тура. Ал с нүктесі х пен х+∆х аралығында жататын себебі, ∆х→0 жағдайда с нүктесі х-ке ұмтылады) . f Функциясы үздіксіз болғандықтан, ∆х→0 жағдайда f(c) →f(x) . Cонымен, ∆х→0 болғанда
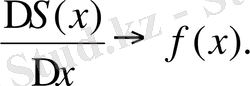 (4) формула дәлелденді.
(4) формула дәлелденді.
Біз S-тің f функция үшін алғашқы екенін шығарып алдық. Сондвқтан алғашқы функцияның негізгі қасиетіне сүйеніп барлық х [а:b] үшін былый жазамыз:
S(x) =F(x) +C
Мұндағы С- қандай да бір тұрақты, ал F-f функциясының алғашқы функцияларының бірі. С шамасын табу үшін х=a мәнін қоямыз: F(a) +C= S(a) =0, бұдан С=-F(a) . Олай болса
S(x) =F(x) -F(a) (5)
Қисық сызықты трапкцияның ауданы S(b) -ге тең болғандықтан, (4) -формулаға х=b мәнін қойсақ, шығатыны:
S=S(b) = F(b) -F(a) .
Енді мысал келтірейік. у=0, х=1, x=2 түзулермен және f(x) =x 2 функцияларымен шектелген қисық сызықты трапецияның ауданын есептеп шығарайық. (3-сурет) .
f(x) =x
2
функциясы үшін F(x) =
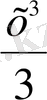 функция алғашқы функциялардың бірі болып табыладыОлай болса,
функция алғашқы функциялардың бірі болып табыладыОлай болса,
S=F(2) -F(1) =
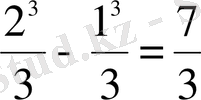
Қисық сызықты трапецияның ауданын есептеп шығару есебіне басқаша тәсіл қолданүға болады. Жеңілдік үшін f функциясын [a; b] кесіндісінде теріс емес және үзіліссіз деп есептейміз. Оған сәйкес қисық сызықты трапецияның ауданын шамамен былайша есептеуге болады.
[a; b] кесіндісін х
0
=a‹x
1
‹x
2
‹…x
n-1
‹x
n
=b нүктелерімен ұзындығы бірдей n кесінділерге бөлеміз және ∆x=
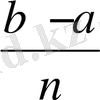 =x
k
-x
k-1
, мұндағы k=1, 2, …, n-1, n болсын. [x
k-1
; x
k
] кесінділерінің әрқайсысын табан ретінде алып, биіктігі f(x
k-1
) , болатын тік төртбұрыш саламыз. Бұл тік төртбұрыштың ауданы мынаған тең
=x
k
-x
k-1
, мұндағы k=1, 2, …, n-1, n болсын. [x
k-1
; x
k
] кесінділерінің әрқайсысын табан ретінде алып, биіктігі f(x
k-1
) , болатын тік төртбұрыш саламыз. Бұл тік төртбұрыштың ауданы мынаған тең
f(x
k-1
) ∆x =
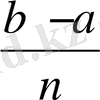 f(x
k-1
)
f(x
k-1
)
ал осындай тік төртбұрыштар (4-сурет) аудандарының қосындысы мынаған тең
S
n
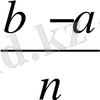 (f(x
0
) +f(x
1
) +…+f(x
n-1
) )
(f(x
0
) +f(x
1
) +…+f(x
n-1
) )
f функциясының үзіліссіз болуы себепті, салынған тік төртбұрыштың бірігуі n үлкен болғанда, яғни ∆х аз болғанда қисық сызықты трапециямен дәл дерліктей келіп беттеседі. Сондықтан n үлкен болғанда S n ≈S деген болжам туындайды. Бұл болжам дұрыс.
Сонымен қатар [a; b] кесіндісінде үзіліссіз ( теріс болмауы шарт емес) кез келген f функциясы үшін S
n
шамасы n→∞ жағдайда қандай да бір санға ұмтылыды. Бұл санды анықтама бойынша f функцичсының а-дан в-ге дейінгі интегралы деп атайды және
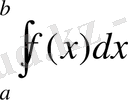 деп белгілейді, яғни
деп белгілейді, яғни
n
 →∞ жағдайда S
n
→
→∞ жағдайда S
n
→
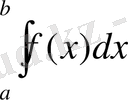
( былай оқылады: икстен эф дэ икстің а-дан в-ге дейінгі интегралы) . А мен в сандары интегралдаудың шектері дееп атайды. а- төменгі, в- жоғарғы шегі. ∫ таңбасы интеграл таңбасы деп аталады. f функциясы- интеграл астындағы функция деп, ал айнымалы интегралдау айнымалысы деп аталады.
Сонымен [a; b] кесіндісінде f(x) ≥0 болғанда сәйкес қисық сызықты трапецияның S ауданы мына формуламен өрнектеледі.
S=
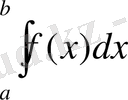 .
.
Интегралды жуық есептеу үшін S n қосындыларын қарастыруға болады. Алайда, мына қосындыларды пайдалану
S
n
=
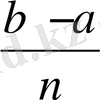 (
(
 f(x
0
) +f(x
1
) +f(x
2
) +…+f(x
n-1
) +
f(x
0
) +f(x
1
) +f(x
2
) +…+f(x
n-1
) +
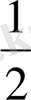 f(x
n
)
f(x
n
)
Мұның қосылғыштары (f фунуциясы оң болғанда) қисық сызықты трапияға іштей сызылған әрі сынықтармен шектелген трапецияның аудандарына тең, бұлар 5-суретте кескінделген.
Шынында да, трапеция ауданының формуласын қолданып мынаны аламыз:
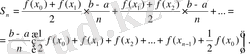
Қисық сызықты трапеция ауданының формулаларын
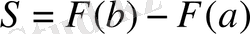 және
және
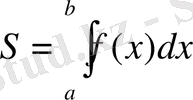
салыстыра отырып, біз мынадай қорытынды жасаймыз.
Егер
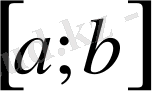 кесіндісінде f үшін алғашқы функция F болса, онда
кесіндісінде f үшін алғашқы функция F болса, онда
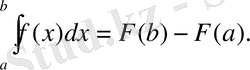 (6)
(6)
формула Ньютон - Лейбниц формуласы деп аталады. Бұл формула
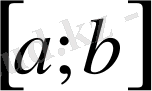 кесіндісінде үзіліссіз кез келген f функциясы үшін тура.
кесіндісінде үзіліссіз кез келген f функциясы үшін тура.
1-мысал. Есептеп шығарайық:
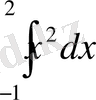
Ал х
2
функциясы үшін алғашқы функциялардың бірі
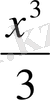 болатындықтан, былай жазамыз;
болатындықтан, былай жазамыз;
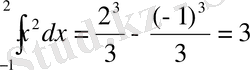
F(b) -F(a) айырымын (F функциясының [a; b] кесіндісіндегі өсімшесін) жазу ыңғайлы болу үшін қысқаша белгілеу қабылданған: F(x)
 , яғни
, яғни
F(b) -F(a) =F(x)

Осы белгілеуді пайдаланып, Ньютон-Лецбниц формуласы әдетте мына түрде жазылады:
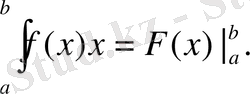 (7)
(7)
2-мысал. Мына интегралды есептеп шығарайық.
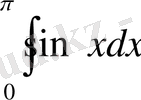 .
.
Енгізілген белгілеулерді пайдаланып, мынаны шығарып аламыз:
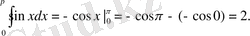
1-ескерту: Интегралға өзіміз берген анықтама бойынша
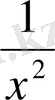 функциясының -1 ден 2-ге дейінгі интеграл жөнінде ештеңе айта алмаймыз, өйткені бұл функция [-1; 2] кесіндісінде үзіліссіз емес. Сондай-ақ
функциясының -1 ден 2-ге дейінгі интеграл жөнінде ештеңе айта алмаймыз, өйткені бұл функция [-1; 2] кесіндісінде үзіліссіз емес. Сондай-ақ
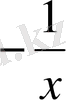 функциясы
функциясы
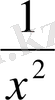 функция үшін осы кесіндіде алғашқы функция болмайды, өйткені кесіндіге тиісті нөл нүктесі функцияның анықталу облысына енбейді.
функция үшін осы кесіндіде алғашқы функция болмайды, өйткені кесіндіге тиісті нөл нүктесі функцияның анықталу облысына енбейді.
2-ескерту: Анықтама бойынша а≥в болғанда
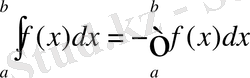
де алып, интеграл ұғымын кеңейте түсу қолайлы. Осы келісім бойынша а мен в-ның кез келген мәндерінде Ньютон- Лейбниц формуласы тура болып қала береді.
Дербес жағдайда
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz