Жүйедегі барлық аспаптардың бос емес болу ықтималдығын есептеу әдісі

Пән: Статистика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:

ЖОСПАР

КІРІСПЕ . . . 3

І ӘДЕБИ ШОЛУ . . . 5

1. 1 Нөлдік және альтернативті болжамдар . . . 5

1. 2 Статистикалық болжамдарды тексеру критерийлері . . . 7

1. 3 Келісімдік критерий ұғымы туралы . . . 9

1. 4 Пирсонның χ² критерийі . . . 11

ІІ Зерттеу ӘДІСТЕРІ . . . 15

2. 1 Талап ағыны шектелмеген жүйені есептеу әдісі . . . 15

2. 1. 1 Қызмет көрсету аспаптарынның бос болу ықтималдығын есептеу әдісі . . . 17

2. 1. 2 Қызмет көрсету к -аспаптарының бос емес болу ықтималдығын есептеу әдісі . . . 17

2. 1. 3 Қызмет көрсету к -аспаптарының бос емес болу ықтималдығын есептеу әдісі. (к жүйедегі талаптар) . . . 17

2. 1. 4 Жүйедегі барлық аспаптардың бос емес болу ықтималдығын есептеу әдісі . . . 17

2. 1. 5 Қызмет көрсету жүйесіндегі талаптың орташа уақытын есептеу әдісі . . . 18

2. 1. 6 Қызмет көрсету жүйесіндегі кезекті күте бастауы орташа уақытын есептеу әдісі . . . 18

2. 1. 7 Кезектің орташа ұзындығын есептеу әдісі . . . 18

2. 1. 8 Жүйеде орналасқан талаптың орташа санын есептеу әдісі . . . 18

2. 1. 9 Қызмет көрсетпей бос тұрған аспаптардың орташа санын есептеу әдісі . . . 18

2. 1. 10 Аспаптардың бос болу коэффициентін есептеу әдісі . . . 19

2. 1. 11 Аспаптардың қызмет көрсетіп, бос емес болуының орташа санын есептеу әдісі . . . 19

2. 1. 12 Аспаптардың тиелу коэффициентін есептеу әдісі . . . 19

ІІІ Зерттеу НӘТИЖЕЛЕРІ . . . 20

3. 1 Көкшетау қалалық медициналық жедел жәрдем станциясына талап ағыны шектелмеген жүйенің тиімділігін есептеу . . . 20

3. 2 Медициналық жедел жәрдем станциясына талап ағыны шектелмеген жүйенің тиімділігін есептеуге арналған программа . . . 23

ҚОРЫТЫНДЫ . . . 28

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР . . . 29

ҚОСЫМШАЛАР

Көпшілікке қызмет көрсету жүйесіне ақпараттық технологияны қолдану

Көпшілікке қызмет етуді ұтымды ұйымдастырудың практикалық талаптары жаңа типті бір топ қызықты математикалық есептерді ұсынды. Алғашында бұл есептер тікелей телефондық станция абонентіне қызмет ету, дүкендердегі сатып алушыларды үзіліссіз қанымдау үшін қор жинаған есептеу сұрақтарына және сатушылар мен сауда кәсіпорындарының кассалар санын ең тиімді етіп құру сұрақтарына қатысты болды.

Бұл теорияның алғашқы дамуына Копенгагенск телефон компаниясының көпжылдық қызметкері, әйгілі дат ғалымы А. К. Эрлангтың (1878-1929) жұмыстары ерекше әсер етті. Оның бұл саладағы зерттеулері 1908-1922 жылға қатысты. Сол уақыттан бері Эрланг ұсынған мәселелерге қызығушылық ерекше жоғарлады. Соның нәтижесінде мұндай мәселемен айналысатын және зерттейтін математиктердің, инженерлердің, сонымен қатар экономисттердің саны едәуір өсті.

Күн сайын өндірістік қызметте және тұрмыста көпшілікке қызмет көрсету қажеттілігі туындайды. Қызмет көрсетуші ұйымдарының қызмет көрсету сұраныстарын қанағаттандыру мүмкіншілікі шектелген. Бұл қағида бойынша кезектің тууына әкеледі. Соған тәрізді мысалдар әр қадамда кездестіріледі: дүкендердегі, билет сататын кассалардағы, автобус және троллейбустардың аялдамасындағы, жедел жәрдем станциясындағы және әскери техникасындағы т. с. с. кезектер. Бірақ келтірілген мысалдар адамның әр-түрлі қызмет аймағынан алынғанымен, олардың барлығына бірдей математикалық аппараттың көмегімен бейнелеуге мүмкіндік беретін формальдық белгі өзіне тән болады. Осымен бірге қызмет көрсетудің сапасымен талап ету жүйесіне қаншалықты дер кезінде қызмет көрсету жүргізілгені түсіндіріледі. Шынымен қызмет көрсету сапасын қалай да сандық түрде бағалау қажет. Осындай бағалаулар үшін көп белгілер жете зерттелінген, әр қайсысының тиімділігі қойылған есептің зерттеуімен анықталады. Ереже түрінде көпшілікке қызмет көрсету жүйесінің зерттеу есебі қажетті қызмет көрсету сапасын қамтамасыз ету үшін ағынның тиімділігін анықтау қажеттілігіне апарады.

Көпшілікке қызмет көрсетумен байланысты барлық есептің ортақ ерекшелігі зерттелінетін құбылыстың кездейсоқ сипаты болады. Олар қызмет көрсетуге талап етудің саны, олардың түсу уақыт аралығы, қызмет көрсету талап уақыт ұзақтығының кездейсоқтылығы болып табылады.

Көпшілікке қызмет көрсету теориясында ақпараттық технологияны қолдану зерттеудің жаңа бір түрін көрсетеді. Зерттеудің өзектілігі кез-келген басқа да жедел жәрдем станцияларында бригада санын тиімді жоспарлауда құрастырылған программаны қолдануға болатындығы.

І ӘДЕБИ ШОЛУ

1. 1 Нөлдік және альтернативті болжамдар

Әрбір ғылым прогресі - болжамдарды ұсынумен және оларды тексерумен байланысты екені мәлім. Ғылымда пайдаланылатын болжамдар өздерінің тұжырымдалу тұрғысынан да, әрі өздері тексеру әдістері тұрғысынан да әр түрлі. Бұлардың ішінде статистикалық болжамдардың алып тұрған орны ерекше. Статистикалық болжам дегенде кездейсоқ шаманың үлестіруі, не үлестіру параметрі туралы болжамды айтады.

Бізге (қазірше) белгісіз кездейсоқ шаманың үлестіруі немесе үлестіру параметрі жайлы ұғым нөлдік (немесе негізгі) болжам Н0 түрінде айтылады. Н0 болжамына қарама-қарсы альтернативті болжам Н1 қойылады. Н0 гипотезасына қарама-қарсы, альтернативті болжамдар бірнешеу (көп) болуы (Н1 Н2, . . . , Нк) мүмкін. Келешекте бір нөлдік Н0 болжамы мен бір Н1 альтернативті болжамын қарастырумен қанағаттанамыз. Ал бұл Н1-дің өзі Н0 -ге қарама қарсы болған бірнеше альтернативті болжамдарды біріктіруі мүмкін.

Сонымен нөлдік болжамды тексеру белгілі статистикалық критерийді пайдалану арқылы орындалады. Ал статистикалық критерий дегенде кездейсоқ тандаманы қай уақытта дұрыс деп қабылдауды, қай уақытта дұрыс емес деп жоққа шығаруды көрсететін ереже деп ұғамыз. Үлестіру параметрі туралы Н0 болжамын тексеретін критерийлерді параметрлік болжамдар деп атайды. Сонымен қатар бағалау үлестіру параметрлерін зерттеу негізінде орындалған үлестіру параметрлік болжамға жатады. Ал параметрлерге жатпайтын болжамдарды параметрлік емес болжамдар деп атайды. Параметрлік емес критерийлер кездейсоқ шаманың үлестіруі жайлы мәліметті қажет етпейді, сондықтан мұндағы критерийлер қарапайым, бірақ параметрлік критерийлерге қарағанда тиімді емес.

Ал статистикалық болжам әр уақытта кездейсоқ тандама ретінде орындалады. Мұндай тандама көлемі шекті болғандықтан бас жиын үлестіруін идеал деп сипаттай алмайды. Сонымен қатар мұндай тандаманы ұйымдастырғанда бас жиын жайында жалған ақпарат беретін сәтсіз тәуекелділік әр уақытта кездесуі мүмкін, яғни статистикалық болжамды тексергенде жалған шешімге келу қаупі әр уақытта туу мүмкін. Олай болса, статистикалық болжамды тексергенде жалған шешімге келу әр уақытта туу мүмкін. Олай болса, статистикалық болжамды қандай бір критерий көмегімен тексергенде мынадай төрт жағдайдың бірі болуы мүмкін.

Дұрыс нөлдік Н0 болжамы қабылданады, ал оған сәйкес альтернативті Н1 болжамы дұрыс емес деп қабылданады.
Жалған нөлдік Н0 болжамы қабылданбайды, ал оған сәйкес альтернативті Н1 болжамы дұрыс деп қабылданады.
Дұрыс Н0 болжамы қабылданбайды, ал оған сәйкес альтернативті Н1 болжамы дұрыс болмаса да қабылданады.
Жалған Н0 болжамы қабылданады, ал оған сәйкес альтернативті Н1 болжамы дұрыс болса да қабылданбайды.

Алдыңғы екі шешімнің дұрыс, соңғы екі шешімнің қате екенін байқау қиын емес. Сонымен қатар, үшінші шешім, дұрыс Н0 болжамын дұрыс емес деу, бірінші текті қателік береді, ал төртінші шешім, жалған Н0 болжамын дұрыс деп қабылдау, екінші текті қателік береді. Бұл айтылғандар мына кестеден түсінікті.

Кесте 1. Болжамды тексеру кестесі.

Н0 болжамы дұрыс

Н0 болжамы дұрыс емес

: Н0 болжамын қабылдамау

Н0 болжамы дұрыс: Бірінші текті қателік

Н0 болжамы дұрыс емес: Дұрыс шешім

: Н0 болжамын қабылдау

Н0 болжамы дұрыс: Дұрыс шешім

Н0 болжамы дұрыс емес: Екінші текті қателік.

Ал статистикалық критерийлермен болжамды тексергенде жіберілген қатенің біреуін болдырмау оны қабылдаудан гөрі құнды болуы мүмкін. Бұл жағдайда мүмкін қатенің қайсысын болдырмауды құнды десек, сонысын бірінші текті қате деп қабылдаймыз. Бұл айтылғандардан шын болжамды дұрыс емес деп қабылдамау бірінші текті қате туғызады деп ұйғаруымызға болады.

1. 2 Статистикалық болжамдарды тексеру

критерийлері

Статистикалық болжамдарды (гипотеза) тексеру критикалық облысы, бар болу деңгейі (мәнділік деңгейі), критерий қуаты (статистикалық критерий қуаты, критерий қуатының функциясы) деп аталатын фундаметальдық ұғымдарға сүйенеді. Колмогоровтың ықтималдылықтар теориясын аксиоматикалық құрудағы жиындар теориясы ұғымын пайдаланып, критерий облысы терминін түсіндіруден бастайық.

Кездейсоқ шама Х мәндерінің жиыны (кеңістігі) V болсын, мұның тәжірбиеде бақылаудан алынған мәндерінен жасалған ішкі жиын W болсын, W ішкі жиыны таңдалған е1, е2, . . . , еm нүктелерінен құрылсын. Бұлардың әрқайсысы бақыланатын кездейсоқ шама Х-тің х1, х2, . . . , хn мәндерінің белгілі жиынтығы болсын. е1, е2, . . . , еm статистикалық сипаттама Е-нің кейбір таңдап алынған сандық мәндері ретінде қарастырылсын және бұл сипаттама туралы Н0 және Н1 болжамдары ұсынылсын. Әдетте нөлдік болжам Н0 кейбір статистикалық критерий С арқылы тексеріледі. Бақылайтын сипаттама Е, яғни таңдалған еі нүктесі критерий облысы (Wi) деп аталатын ішкі W жиын ішіндегі тағайындалған (белгілі) облыста ғана болса, Н0 болжам ы қабылданбайды. Ал егер бұл бақылап отырған сипаттама Wi-W облысы шешімді қабылдау облысы деп аталады. Болжамды тексереиін критерийді таңдау мен критерий облысын таңдаудың эквиваленттігін байқау қиын емес, сондай-ақ болжамды тексеру дегенде критерий облысын (критерийді) тандау деп түсінеміз.

Болжамды тексерудің негізгі мақсаты шешімді қабылдау қатесін азайту болмақ. Сонымен қатар, екінші қатені жіберуден гөрі, бірінші текті қатені жібермеу маңызды. Олай болса, статистикалық критерий, демек критерий облысы, егер Н0 болжамы дұрыс болса, онда бақылаудан алынған еі критерий облысында (Wi - да) мүмкіндігінше сирек болатындай етіп алынуға тиісті. Осы мақсатпен қалауымызша аз α саны тағайындалады, мұны мәңділік деңгейі деп атайды. Сөйтіп бірінші текті қатенің ықтималдылығын Н0 болжамының дұрыстығын тексергенде осы деңгейден артпауын талап етеді. Сонымен критерий облысы, болжамның статистикалық сипаттамасы және мәнділік деңгейі арасында мынандай қатыстық бар: Н0 болжамын дұрыс десек, онда критерий облысы Wс -да болатын. Е сипаттамасының сандық мәндерін қабылдау ықтималдығы мәнділік деңгейі α-дан артпауы тиіс.

Мәнділік деңгейін тандау практикалық мұқтаждықтан анықталады, дәлірек айтсақ, күтетін бірінші текті қате зияндығымен анықталады. Бұл қаншалықты құнды болса, соншалықты мәнділік деңгейі аз болу керек. Әдетте, көптеген практикалық есептерді шешуде α=0, 05 мәнділік деңгейі пайдаланылады. Ал кейбір қатандықты талап ететін есептерде α-ның мәнін кем (мысалы α=0, 01) алады, ал кейде α=0, 10 деп те аталатын есептер бар. Бұларды бұлай ұғу керек: α=0, 05 (α=0, 01; α=0, 10 т. б. ) десек, онда 100 бақылаудың 5-тен артық емес жағдайында біздің болжамымыз дұрыс болуы мүмкін, сондай-ақ 95-тен артық бақылауда тандамада дұрыс болады деп ұйғаруды айтамыз.

Мәнділік деңгейін таңдағанда бірінші текті қатені жіберу ықтималдылығы нөлге жақын болатындай етіп алуға бола ма деген сұрақ өзінен-өзі туады. Бұл сұраққа жауап берерде α=0 дейік. Ол уақытта тәжірибенің нәтижесіне байланыссыз нөлдік болжам Н0 дұрыс (шын) болса да, жалған болса да қабылданады. Ал жалған болған Н0 болжамын қабылдасақ, екінші текті қате жіберетініміз белгілі, α-ны шексіз азайта берсек, онда екінші текті қателігі арта береді де қолайсыз нәтижеге әкеледі. Сонымен, бірінші текті қате ықтималдылығын кеміте берсек, онда екінші текті қате ықтималдығы β-ны қолайсыз ұлғайта беру қаупі туатының еске тұту қажет.

Ал α мен β ықтималдықтарының тиімді арақатынасын критерий облысын сәтті тандау арқылы жетеміз. Мұндай тандау шарты төмендегіше орындалады. Н0 болжамын дұрыс болғанда тандалған статистикалық сипаттама еі мәні критерий облысы Wс -да болса, яғни

P{ еіЄ Wс / Н0 }=α

болса, онда Н0 дұрыс болмағанда және Н1 дұрыс болмағанда осы еі мәнінің Wс облысында болу ықтималдығы

P{ ІіЄ Wс / Ні }=max

болуға тиісті. Бұл жағдайда екінші текті қате, яғни дұрыс болжам Н1 -ді қате деп қабылдамау, ықтималдылық β мәні минимум болады. Тұжырымдасақ, соңғы талап С критерий қуатының постулаты делінеді. Бұл екінші текті қатеніжібермеу ықтималдылығымен өлшенеді.

Статистикалық болжамдар теориясының толық баяндаулары Нейман, Пирсон, Романовский, Крамер, Леман еңбектерінде баяндалады. [ Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. Москва 1979г, стр. 235-245]

1. 3 Келісімдік критерий ұғымы туралы

Статистикалық болжамдарды үлестірудің параметрін мыңыздылыққа тексеруге пайдалану туралы сөз еттік. Бірақ статистикалық практикада екі үлестірудің бір-біріне жақын болуын, анықтау мәселелері жиі кездесеі. Бұл сиықты есептерді шешу статистикалық болжамдарды тексеру арқылы орындалады. Мұндай есептердің шешудің жалпы схемасы мынадай болады: таңдаманың тәжірбиелік үлестіруі белгілі болғанда (бұл f, f*, n, n* түрінде де берілуі мүмкін) . Сәйкес бас жиынтықтың теориялық үлестіруімен (бұл-жиіліктің математикалық күтімі, ықтималдылықтардың үлестіруі жиынтық жиіліктің математиаклық күтімі немесе жиынтық ықтималдықтар үлестіруі болуы мүмкін) салыстырылатын болады. Сөйтіп, таңдаманың тәжірибелік үлестіруі мен теориялық үлестіруінің айырмашылығы маңызды емес деген нөлдік болжам Н0 ұсынылады. Ал үлестіру заңы әр түрлі, мысалы үлестіру тығыздығы f`(х), интегралдық үлестіру F(х) т. т. түрінде берілуі мүмкін.

Нөлдік болжам Н0 -ді қабылдау үшін немесе қабылдамау үшін кейбір статистикалық сипаттаманы құрады. Осы сипаттама арқылы тәжіриебелік үлестіру айырмашылығы дәрежесінің қандай екенін анықтайды. Бұл сипаттама W шамасын әртүрлі тәсілдермен алуға болады, мысалы, жиілік пен математикалық күтім айырымы квадратының қосындысы W=Σ[F-M(F) ] ² немесе тәжірибелік интегралдық функция Fn (x) пен теориялық интегралдық функция F(x) айырымының ауытқуының максимум мәні алынуын мүмкін т. т.

Осы аталған тәсілдердің бірінен құрылған статистикалық сипаттама W кездейсоқ шама болады және мұның үлестіру заңы кездейсоқ шама Х-ке (Х=f, f*, F, F*) және сыну саны n-ге. Сонымен Н0 болжамы дұрыс болса, онда статистикалық сипаттама W заңы кездейсоқ шама Х пен n санының теориялық үлестіру заңымен анықталады.

Енді үлестіру заңы белгілі делік. Жоғарыда айтылғандай тәжірибелік үлестіру мен теориялық үлестіру айырмашылығын көрсететін шекаралық мән Wm-мен анықталады дейік. Ол уақытта Р (W< Wm) ықтималдық мәні үлкен болса, онда Н0 болжамын қабылдауға болады, ал ықтималдық мәні аз болса, онда тәжірибелік мәлімет Н0 болжамын қабылдауға қайшы келеді дейміз, сөйтіп Н0 -ді қабылдамай, оның орнына альтернативті болжам Н1 -ді қабылдаймыз, яғни белгілі ықтималдықпен теориялық үлестіру мен тәжірибелік үлестіру айырмашылығы маңызды дейміз.

Ендігі мәселе осы статистикалық сипаттама W -ны қалай құруға болатынын анықтауда жатыр. Көп жағдайда f`(х), Ғ(х) үлестірулері белгісіз болып келеді, сондықтан W-нің үлестіру f`(х), Ғ(х) заңы үлестірулері мен олардың параметрлеріне тәуелсіз деп алынған қолайлы болмақ. Мұндай критерийлер ішінде көп қолданылып жүргендері К. Пирсонның χ² (хи-квадрат) критерийі. [Гмурман В. Е. Теория вероятностей и математическая статистика. Москва 1977г. Стр. 281-296]

1. 4 Пирсонның χ² критерийі

Бұл критерийді қолдану төмендегі талқылауға сүйенеді. n бақылау жүргізгенде кездейсоқ шама (белгі) Х қандай да анық мәндерді қабылдасын және олар k интервалға (2-кестедегідей) топталсын бейік. Х кездейсоқ шамасының үлестіру заңы белгілі болсын, ол интегралдық функция Ғ(х) немесе үлестіру тығыздығы f`(х) түрінде берілсін дейік. Бұл заңды білген соң әрбір k-интервалда болатын рk ықтималдықты анықтауға болады.

Ендігі қарастыратын мәселеміз тәжірибеден алынған f`1 (не Ғi жиілік χ үлестіруі мен рi ықтималдықтардың) немесе сәйкес nрі математикалық күтімінің теориялық үлестіруінің келісілетінің мақұлдайтын Н0 болжамын тексеру болмақ.

Ақылға салатын болсақ, онда f`i мен рi айырымы аз болса, Н0 болжамын қабылдауымызға болмайды. Бұл айырым өлшеуі ретінде f`i - рi ауытқуы квадратының салмақтық қосындысы өрнегін

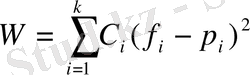
Кесте 2. Варианттар интервалын көрсететін кесте.

Варианттар интервалдары

(х1, х2)

(х2, х3)

. . .

(х2, х3)

Варианттар интервалдары: Интервалдағы Х мәнінің саны (жиілігі)

(х1, х2): n1

(х2, х3): n2

. . .: . . .

(х2, х3): Nk

: N

Варианттар интервалдары: Салыстырмалы жиілік

(х1, х2): f1

(х2, х3): F2

. . .: . . .

(х2, х3): f2k

: L

Варианттар интервалдары: Жиіліктің математикалық күтімі

(х1, х2): Nр1

(х2, х3): nр2

. . .: . . .

(х2, х3): nр2k

: N

Варианттар интервалдары: Интервалдағы Х-тың ықтималдығы

(х1, х2): р1

(х2, х3): р2

. . .: . . .

(х2, х3): р2k

: L

алуға болады. Әрбір интервалға сәйкес келетін ауытқулар бірдей болмағандықтан, сi салмақтық коэффициентін енгізуге тура келеді. Өйткені рi үлкен болғанда бұл ауытқуға аз болуы мүмкін де, рi ықтималдылығына кері пропорционал шаманы алған жөн. Пирсон салмақтық коэффициент мәніне сi=n/рi қатынасын алған қолайлы деп сi-дің бұл мәнін ескеріп, W-ны былай жазады:

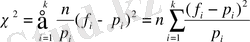
немесе қолайлы болу үшін

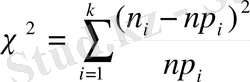
Мұнда ni=nf`i. Тәжірибелік үлестіру мен теориялық үлестіру айырмасын көрсететін бұл өрнектерді Пирсонның χ² (хи-квадрат) критерийі деп атайды.

χ² кездейсоқ шамасын үлестіруі f`(х) немесе Ғ(х) үлестіру заңы - n-ге тәуелсіз, ол v-ге ғана тәуелді. Олай болса, n→∞ χ² үлестіруі бұрыннан бізге мәлім k-1 еркіндік дәрежесі бар χ² үлестіруіне ұмтылады.

Сонымен χ² критерийінің үлестіруі мен χ² үлестіруінің бір-біріне жақындауы эмпирикалық үлестіру мен теориялық үлестірудің сәйкес келуі жайлы болжамды тексеру үшін мәңділік деңгейдің берілуі бойынша критерий облысын құруға мүмкіндік береді. Еркіндік дәрежесінің саны

v=n-1, мұндағы n - бақылау саны, l - статистикалық тәсіл берілгенде осы бақылауға қойылатын сызықты тәуелділіктер саны. Егер l =1 болса, онда ол байланыс кездейсоқ шамалар қосындысы n-ге теңдігін білдіреді, ол

niΣ fi = 1 немесе n= Σni болады. Ал l =2 болса, онда бұл байланыстан басқа тағы да бір байланысты көрсететін параметр бар дегенді білдіреді. Мысалы, биномдық және Пуассон үлестіруінде l =2, өйткені біріншіде р параметрі, екіншіде λ параметрі кездейсоқ шамалар арасындағы тәуелділіктің тағы да біреуінің бар екенің көрсетеді. Ал нормал заңында болса, х пен s параметрлері бар.

χ² қисығының формасы осы еркіндік дәрежесі v-ге байланысты. Өйткені v қанша аз болса, қисық бір жағына қисая ауып, асимметрия күшейе түседі де v→∞ χ² қисығы қалыпты қисыққа ауады. Шынында, χ² шамасы 0-ге тең болса, онда(ni - Σ=nрi) ² немесе (f`i -рi ) ² қосылғыштарының барлығы да 0-ге болады, яғни тәжірибелік жиілік пен ықтималдық бір-біріне дәл тең болып, эмпирикалық үлестіру мен теориялық үлестіру толық беттеседі. Басқа жағдайларда χ² мәні 0-ге тең болмайды, сөйтіп (f`i -рi ) ² айырымы үлкен болған сайын χ² мәні үлкен бола береді. Ал бұл айырым қандай да бір деңгейден арта бастаса, онда χ² мәні Н0 болжамын қабылдау облысынан Н0-ді қабылдамайтын критерийлік облысқа өтеді.

Сонымен χ² критерийімен Н0 нолдік болжамын тексеру алгоритмі төмендегіше орындалады.

Бұрын жүргізілген тәжірибеден алынған мәліметтерге сүйене отырып, кездейсоқ шама Х-тің ұйғарылып отырған үлестіру заңы таңдалады.
Тәжірибеден алынған жиіліктер интервал бойынша топтастырылады. Ал кейбір интервалдарға сәйкес жиіліктер аз болса, (әдетте 5-тен кіші болса), олар бір интервалға біріктіріледі.
Таңдалынған үлестіру заңы бойынша ықтималдылықты (математикалық күтімді) есептейді.
Формулалар бойынша χ² мәні есептеледі.
Еркіндік дәріжесі v саны v=k- l-ді анықтайды, мұнда k-интервалдар саны, l- байланыс саны.
Берілген мәндік деңгейімен еркіндік дәрежесі саны арқылы Н0 болжамын қабылдау облысынан ауытқудың критерийлік облысынан бөліктейтін шекаралық χ²ш (χ²ш = χ²q, v) мәнін табамыз.
4-ші пунктте есептелген мәнін шекаралық мән χ² ш пен салыстырады:

А) егер χ² <χ² ш болса, онда Н0 болжамы қабылданады, яғни тәжірибелік үлестірумен теориялық айырмасы аса маңызды емес. Демек Пирсон критерийінің мәні қабылдау облысында жатыр дейміз;

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.