Цифрлық электроника негіздері: Буль алгебрасы және комбинациялық цифрлық құрылымдар


Мазмұны
Алғы сөз . . . 3
І-тарау. Буль алгебрасыныҢ
негІзгІ маҒлҰматтары . . . . . . ………4
1. 1. Логикалық айнымалылар және функциялар . . . … . . . …. . 4
1. 2. Буль алгебрасының негізгі функциялары ……… . . . ………. . …. 8
1. 3. “Емес”-”Жоққа шығару” (“Инверсия”) -
“Кері айналдыру” логикалық функциясы . . . …. . 9
1. 4. “Конъюнкция” (“Және”-”и”) функциясы … . . . 10
1. 5. “Немесе” - ”Или” - ”Дизъюнкция”
логикалық функциясы . . . ……. . 11
1. 6. “Және - жоққа шығару” -
”шеффер” (”и - не”) логикалық функциясы . . 12
1. 7. “Немесе - жоққа шығару” -
”Пирс” (”или - не”) логикалық функциясы . . . . . 12
1. 8. “Бірмәнділік” (равнозначность-
эквивалентность) -”Исключающее или-не”,
Әрмәнділік”(неравнозначность) -
”Исключающее или” функциялары . . . . 13
1. 9. “ Шеффер ” логикалық функциясының
жан-жақтылығы . . . . 16
1. 10. “Инверсия” функциясын пайдаланып
бір логикалық функцияны екінші логикалық
функцияға айналдыру . . . …. . 17
1. 11. Толықтауыш функциялар . . . ………. . 18
1. 12. Буль алгебрасының постулаттары . . . ………. . 19
1. 13. Буль алгебрасының заңдары . . 20
1. 14. Де Морган постулаттары . . . 20
1. 15. “0” мен “1” үшін күмәнсіздік функциялары
(функция конституенты ”1” и “0”) . . . 21
1. 16. Дизъюнктив және Конъюнктив түрлерінде
берілген логикалық функциялар . . ……. 22
ІІ-тарау. ЛогикалыҚ элементтердІҢ
Қолданылуы . . . ……27
2. 1. Буль қатынастарын пайдаланып электрондық
жүйелерді құрастыру . . . …. . 27
2. 2. Логикалық функциясының ақиқат кестесінен
оның аналитикалық өрнегіне көшу әдістері . . 29
2. 3. Логикалық функцияны ықшамдау . . . 30
2. 4. Карно картасы . . . ……. 31
2. 5. Аралас цифрлік құрылымдарды талдау
және құрастыру . . . ……. 34
ІІІ-тарау. АРАЛАС КомбинациялыҚ
цифрлыҚ ҚҰрылымдар . . . 35
3. 1. Жұмбақ сандар (коды), жұмбақтауыш
құрылымдар (шифраторы), жұмбақ шешуші
құрылымдар (дешифраторы) . . . 35
3. 2. Екілік - ондық 8421 жұмбақтау жүйесі . . . 35
3. 3. “3-ке арттыру әдісіне” негізділген жүйе . . . …. . 37
3. 4. Дешифраторлар-декодерлер . . . 37
3. 5. Мультиплексорлар . . . . 40
3. 6. Демультиплексорлар . . . . 42
3. 7. Шифраторлар . . . 44
3. 8. Сумматорлар . . . ……. 45
3. 9. Субтракторлар-алғыштар (вычитатели) . . . 49
3. 10. Цифрлық кoмпараторлар . . . 52
Қазақша-орысша сөздік . . . . . . 53
Орысша-қазақша сөздік . . . . . 64
Тест . . . 75
Қорытынды . . . 93
Әдебиеттер . . . 94
А л ғ ы с ө з.
Тәуелсіздік алып, егемен ел болуымыздың арқасында қазақ тілінің мәртебесі өсіп, Қазақстан Республикасының мемлекеттік тілі болып жарияланды. Осы себептен барлық жоғарғы оқу орындарында, ғылыми мекемелерде оқуды және іс қағаздарын қазақ тілінде жүргізу қолға алынуда. Екінші жағынан республикамызда қазақ мектептері мен жоғарғы оқу орындарында қазақ бөлімдерінің көптеп ашылуы халық ағарту қызметкерлері алдында жаңа міндеттер қойды. Олардың бастысы қазақ-орыс және орыс-қазақ қостілдігін одан әрі үйлесімді дамыту, барлық пәндерден жаңарған оқулықтар мен оқу құралдарын қазақ тілінде жазып жеткілікті мөлшерде жедел бастырып шығару.
Ана тілінде оқулықтар мен көмекші оқу-әдістемелік құралдардың жетіспеуі ғылым мен техниканың электроника сияқты алдыңғы қатардағы саласына арнап оқу құралын жазуды қазіргі таңдағы әрі жауапты әрі маңызды істердің біріне айналдырып отыр. Бұрынғы Кеңес Одағы мен Ресейде жарық көрген кітаптарды тікелей аударып, оны не оқу құралы не оқулық ретінде пайдалана беру мүмкіндігі бар болғанымен, ол онша мақтанарлық жәй емес. Осы орайда ұсынылып отырған дипломдық жұмыс аталған кемшіліктерді біршама бейтараптап қазақ тілінде оқитын оқушылар мен студенттерге “Цифрлық электрониканың” негізін жете түсініп, оның тұжырымдарын өмірде еркін пайдалануға мүмкіндік беретін құрал.
Сондықтан ұсынылып отырған дипломдық жұмыста кездесетін терминдердің аудармалары ретінде қолданылған әдебиеттер тізіміндегі сөздіктердегі аудармаларымен қатар, олардың қазақ тіліндегі терезесі тең болатындай баламалары да пайдаланылады. Оқушыға ыңғайлы болу үшін жұмыстың соңында қазақша - орысша және орысша - қазақша сөздік берілген. Жұмыс шартты түрде екі бөлімнен тұрады деп қарастыруға болады. Бірінші бөлімінде цифрлық электрониканың негізі болып табылатын Буль алгебрасынан мағұлматтар келтірілген. Оқушыны “логикалық айнымалы”, “логикалық функция”, “логикалық амалдар” ұғымдарымен таныстырады. Буль алгебрасының теңдіктері, теоремалары берілген. Екінші бөлімінде цифрлық электрониканың қарапайым құраушылары және олардың көмегімен цифрлық электрониканың күрделі құрылғыларын құрастыру мүмкіндіктері көрсетілген. Цифрлық электрониканың “тізбектелген” және “комбинациялық” құрылғыларының логикалық сызба жобалары, олардың жұмыстарын анықтайтын ақиқат кестелерімен логикалық функцияларының аналитикалық түрлері көрсетілген. Аналитикалық өрнек түрінде берілген логикалық функцияларды ықшамдау, логикалық функциялардың тағайындайтын амалдарын орындайтын электрондық жобаларды құрастыру әдістері де баяндалған. Үшінші бөлімді оқу құралында пайдаланған сөздер бойынша құрастырылған сөздік берілген.
І тарау. Буль алгебрасыныҢ негІзгІ маҒлҰматтары.
1. 1 Логикалық айнымалылар және функциялар.
Цифрлық құрылым оның кірісіндегі дабылдың жұмбақ сандарынан (Х 1 , Х 2 , . . . Х n ) логикалық амалдарды қолдану арқылы дабылдың қажетті (шығысындағы) жұмбақ сандарын (Y 1 , Y 2 , . . . Y m ) алуға мүмкіндік береді. Қолдануға қажетті логикалық амалдардың жиынтығын - логикалық функцияларды - математикалық логика (Буль алгебрасы) заңдылықтарына сүйеніп анықтайды. Цифрлық электроника құрылымының күйін, жұмыс істеу барысын сипаттау үшін Буль алгебрасының “логикалық айнымалы”, “логикалық функция” деген ұғымда-рын пайдаланады. Логикалық айнымалылар ретінде төмендегі-дей қосалқы тұжырымдар қолданылады: “шын” - ”өтірік”, не “ақиқат” -”жалған” , не “иә”-”жоқ” , не “1”-”0”. Логикалық айнымалылардың “1” және “0” мәндері көбірек пайдаланылады. (Ескерту: Логикалық айнымалылардың “1”, “0” мәндеріне арифметикалық амалдар қолдануға болмайды) . Логикалық айнымалылар шаппа, айырғыш - қосқыш т. т. сияқты нысандар-дың күйлерін (ашық - жабық, немесе, қосылған - қосылмаған, немесе, бар - жоқ, сияқты күйлерін) өте дәл сипаттайды.
Сонымен, цифрлік электроникада логикалық айнымалы-лар екі логикалық тұжырымдарға сәйкесті “1” және “0” мән-дерін қабылдайды.
Логикалық функция логикалық айнымалыларға қолданы - латын логикалық амалдарды анықтайды. Логикалық функциялар Ү 1 , Ү 2 , …, Ү m логикалық айнымалылардың мәндерінің комбинацияларына және оларға қолданылатын логикалық ама - лдар жиынтығына байланысты не “логикалық ақиқат” - “1”, не “логикалық жалған” - “0” тұжырымдарын тағайындайды, қабылдайды.
Әрқайсысы тек “0” немесе “1” мәндерін қабылдайтын саны К - ға тең логикалық айнымалылардың әртүрлі комбина-цияларының саны 2 к - ға тең. Мысалы, логикалық айнымалылардың саны К = 2 болғанда, олар арқылы құрылатын комбинациялардың саны 2 2 = 4 ке тең: х 1 х 2 = 00, 01, 10, 11. Логикалық айнымалылардың әр комбинациясына және олардың араларындағы қолданылатын логикалық амалдарға байланысты логикалық функция не “логикалық ақиқат” - “1”, не “логикалық жалған” - “0” тұжырымдарын тағайындайды.
Саны К - ға тең логикалық айнымалыларға тәуелді логи-калық функцияларды үш логикалық амалдарды: “логикалық жоққа шығару” ( - ), “логикалық қосу” ( + ; v ), “логикалық көбейту” (Š ; ∧ ; &) пайдаланып құрастыруға болады. Логика-лық тұжырымдардың өзара тепе-теңдігін ( = ) белгісі арқылы көрсетеді.
Төменде 1. 1. 1 - кестеде “логикалық жоққа шығару”, “ло-гикалық қосу”, “логикалық көбейту” амалдарын х 1 және х 2 логикалық айнымалыларына қолдану арқылы логикалық “жоққа шығару” - ”инверсия”, “логикалық қосу” - ”дизъюнкция”, “логикалық көбейту” - ”конъюнкция” логикалық функцияларын құрастыру мысалдары көрсетілген.
Бұл кестені
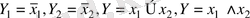 логикалық функцияларының ақиқат кестесі дейді. Сонымен,
ақиқат кесте логикалық функциялардың логикалық айнымалыларының мәндерін және оларға қолданылатын логикалық амалдарымен анықталатын логикалық тұжырымдарды тағайындайды.
логикалық функцияларының ақиқат кестесі дейді. Сонымен,
ақиқат кесте логикалық функциялардың логикалық айнымалыларының мәндерін және оларға қолданылатын логикалық амалдарымен анықталатын логикалық тұжырымдарды тағайындайды.
1. 1. 1 - к е с т е .
Логикалық
айнымалы-
лар
Логикалық
“жоққа шығару”
-”инверсия”
функциясы
“логикалық
қосу”-”ди-
зъюнкция”
функциясы
“логикалық көбейту”-
”конъюнкция”
функциясы
x 1
0
0
1
1
x 2
0
1
0
1
Y 1 = x 1
1
1
0
0
Ү 2 = x 2
1
0
1
0
Ү = x 1 ∨ x 2
0
1
1
1
Ү = x 1 ∧ x 2
0
0
0
1
Сонымен логикалық функцияларды екі әдіспен
Буль ал-гебрасының өрнектері
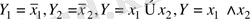 арқы-лы (аналитикалық өрнек әдісі), не кестеге толтырылған мәндер (ақиқат кестесі) арқылы беруге болатындығын көреміз.
арқы-лы (аналитикалық өрнек әдісі), не кестеге толтырылған мәндер (ақиқат кестесі) арқылы беруге болатындығын көреміз.
Логикалық айнымалы, әсіресе, логикалық функция ұғым-дарын тереңірек түсіну үшін мына төмендегі өмірден алынған мысалдарды қарастырайық.
1 - мысал ретінде абитуриенттің оқуға түсу мүмкіндігін қарастырайық. Егер жолға ақша болса, емтиханнан жеткілікті ұпай алса, абитуриент жоғарғы оқу орнына түседі деген тұжы-рымды логика алгебрасының қағидалары арқылы өрнектейік. Мұнда оқуға түсу түспеуін анықтайтын логикалық Ү - функциясының мәні екі: х 1 - жолға ақшаның бар - жоқтығын (“бар” - ”1”, “жоқ” - ”0”), х 2 - емтиханнан жеткілікті ұпай алған - алмағандығын көрсететін х 1 және х 2 логикалық айнымалардың мәндеріне байланысты. Сондықтан, абитуриенттің оқуға түсу - түспеуін анықтау үшін х 1 , х 2 логикалық айнымалылардың мәндерінің әртүрлі комбинацияларымен және олардың арасында қолданылатын логикалық амалдармен анықталатын логикалық Ү - функциясының мәндерін анықтауымыз керек.
Абитуриенттің оқуға түсуін анықтайтын “иә түсемін” деген оң жауап алу үшін, яғни логикалық Ү - функциясының мәні “иә” - ”1” деген мән қабылдау үшін, логикалық х 1 , х 2 ай-нымалылар бір мезгілде, қатарынан “1” - мәнін қабылдаулары керек. Басқаша айтқанда, логикалық айнымалылар “1” - мәнін қабылдап олар өзара “және” деген сөзбен жалғастырулары керек. Яғни, х 1 = 1 және х 2 = 1 болса Ү = 1 болады. Ал, егер екі логикалық айнымалылардың ең болмағанда біреуі “0” деген мән қабылдаса Ү - функциясы “0” мәнін қабылдап, “жоқ” - ”жоқ абитуриент оқуға түспейді” деген теріс логикалық тұжы-рым алынады.
Қорытынды:
Абитуриенттің оқуға түсу түспеуін анықтау үшін, яғни х 1 , х 2 логикалық айнымалыларына тәуелді логикалық Ү - функциясының мәндерін анықтау үшін;
- бірінші, х 1 , х 2 логикалық айнымалыларының мәндерінің жиынтықтарының комбинацияларын: 0, 1; 1, 0; 0, 0; 1, 1 табу керек;
- екінші, айнымалылардың мәндерін “және” деген логикалық сөзбен жалғастыруымыз керек: “0” және”1”, не “1” және ”0”, не “0” және “0”, не “1” және “1”. Логикалық алгебра тілімен айтқанда х 1 , х 2 айнымалылары өзара “логикалық кө-бейтілулері” керек.
Логикалық көбейту функциясының ( Ү ) логикалық айнымалыларға тәуелділігі не
Ү = х 1 . х 2 ; Ү = х 1 × х 2 ; Ү = х 1 ∧ х 2 (1. 1. 1)
өрнектерінің бірімен, не төмендегі 3. 1. 1- ақиқат кестесімен беріледі. (1. 1. 1) - өрнегімен 1. 1. 1- кестесіндегі “ . ”, “ד, “∧“ белгілер “логикалық көбейту” амалының әртүрлі таңбалары.
Екінші мысал ретінде “Жигули” мәшинесін сатып алу - алмау мәселесін қарастырайық.
Жигули мәшинесін сатып алу мүмкіндігі мына жағдайларға байланысты: біріншіден, мәшинені сатып алу қажеттігі бар - жоқтығына, екіншіден, сатып алушыда мәшинені жүргізуге рұқсат қағаз бар - жоқ екендігіне, үшіншіден, мәшинені сатып алуға жеткілікті ақша бар - жоқтығына байланысты.
1. 1. 2 - к е с т е
0
0
1
1
0
1
0
1
0
0
0
1
Бұл жағдайларды логикалық айнымалылар деп атап, мәшинені сатып алу мүмкіндігін мына төмендегі 1. 1. 2 - кестедегідей жүйелеп көрсетуге болады.
Сонымен мәшинені сатып алу мәселесі үш жағдайдың ор-ындалуына байланысты. Жоғарыдағы үш сұрақтың үшеуіне де бір мезгілде - қатарынан “иә” деген оң жауаптар алынғанда ғана “иә” мәшине сатып алуға болады деген оң қорытынды
1. 1. 3 - к е с т е
алынады. Ал, егер үш сұрақтың ең болмағанда біреуіне “жоқ” деген жауап алынса, онда “жоқ мәшине сатып ала алмаймыз” деген теріс логикалық тұжырым алынады.
Сонымен, мәшинені сатып алуға жол ашатын “иә” деген оң жауап алу үшін, біріншіден, қойылған үш сұраққа да “иә” деген үш жауап алынуы керек, екіншіден ол логикалық жауаптар бір-бірімен “және” деген сөзбен өзара жалғанулары керек, яғни “иә” деген жауаптардың арасында міндетті түрде “және” деген сөздер болуы керек.
Математикалық логикада “иә” деген логикалық жауаптарды логикалық айнымалылар дейді, ал олардың өзара байланыстарын, қарым-қатынасын, яғни логикалық айнымалыларға қолданылатын логикалық амалдарды анықтайтын “және” деген логикалық сөздерді логикалық функция дейді. “және” логикалық функция “логикалық көбейтуді” анықтайды, яғни “және” деген сөзбен жалғанған логикалық айнымалылар өзара “логикалық көбейтілуі” керек.
Ал, жоғарыдағы үш сұрақтың ең болмағанда біреуіне “иә”, ал қалғандарына “жоқ” деген жауап алынған күнде мәшинені сатып алу-алмауын анықтайтын “иә” деген оң логикалық жауап алыну үшін олар өзара “немесе” деген логикалық сөзбен жалғастырылуы керек. Бұл жағдайда логикалық айнымалыларды байланыстыратын “немесе” деген логикалық сөз логикалық функция болады. “немесе” деген логикалық функция “логикалық қосу” амалын анықтайды, яғни “немесе” деген логикалық сөзбен жалғастырылған логикалық айнымалылар өзара логикалық қосылуы қажет.
Логикалық қосу математикалық логикада “+” не “V” таң -баларымен белгіленеді.
Қалай болса да “және”, “немесе” логикалық функцияларының мәндері “иә” не “жоқ” деген логикалық жауап болу керек .
Логикалық функциялар мәндерінің логикалық айнымалыларға байланысын ақиқат кестесі арқылы беруге болады.
Аргументтері “иә” - “1”, “жоқ” - “0” логикалық айнымалылары болатын және логикалық функциясының ақиқат кестелері төмендегі (1. 1. 4) және (1. 1. 5) кестелерінде берілген.
1. 1. 4 - к е с т е
ақша бар ма?
- Б
жѕргізуге рұқсат қа-ғаз бар ма?
- Ә
қажетті ақша бар ма?
- А
мәшине сатып алынды
ма?
0
1
2
3
4
5
6
“жоқ”
“жоқ”
“жоқ”
“жоқ”
“иә”
“иә”
“иә”
“жоқ”
“жоқ”
“иә”
“иә”
“жоқ”
“жоқ”
“иә”
“жоқ”
“иә”
“жоқ”
“иә”
“жоқ”
“иә”
“жоқ”
“жоқ”
“жоқ”
“жоқ”
“жоқ”
“жоқ”
“жоқ”
“жоқ”
1. 1. 5 − к е с т е
ақша бар ма?
- Б
мәшинені жүргізуге рұқсат қағазы бар ма?
- Ә
Мәшине- ні сатып алу қажеттігі бар ма?
- А
сатып алынды
ма?
0
1
2
3
4
5
6
“0”
“0”
“0”
“0”
“1”
“1”
“1”
“0”
“0”
“1”
“1”
“0”
“0”
“1”
“0”
“1”
“0”
“1”
“0”
“1”
“0”
“0”
“0”
“0”
“0”
“0”
“0”
“0”
1. 2. Буль алгебрасының негізгі функциялары.
Буль алгебрасының негізінде “және” - ”конъюнкция”, “немесе” - ”или” - ”дизъюнкция”, “инверсия” (“жоққа шығару” , не “емес”, не “кері айналдыру”) , т. т. функциялары жатады. Осы функцияларды жеке-жеке қарастырайық.
1. 3. “Емес”-”Жоққа шығару” (“Инверсия”) - “Кері айналдыру” логикалық функциясы.
“Жоққа шығару”-”инверсия” логикалық функциясы логикалық тұжырымды жоққа шығарып, кері тұжырымға айналдырады. “Инверсия” функциясының әсерінен “иә” тұжырымы “жоқ” тұжырымына, яғни логикалық “1” логикалық “0”-ге айналады және керісінше логикалық “0” логикалық “1”- ге айналады.
“Инверсия” функциясын (Ү) логикалық айнымалының төбесінде сызылған сызықпен көрсетеді:

Бұл функция былай оқылады: “игірік x 1 емес”, “игірік x 2 емес”.
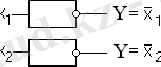
“Инверсия” функциясы сызба бейнелерде мына таңбала-рымен белгіленеді :
 1. 3. 2
1. 3. 2
1. 3. 2 - сурет. “Инверсия” логикалық функциясының сызба жобадағы шартты белгісі.
“Жоққа шығару” - ”инверсия” функциясының қызметін тағайындайтын амалын мына төмендегі электр тізбегі арқылы жүзеге асыруға болады.
1. 3. 3
1. 3. 3 - сурет. “Инверсия” логикалық функциясының тағайындайтын логикалық амалдарын жүзеге асыруға арналған электр тізбегі.
“Инверсия” функциясының ақиқат кестесі мынандай:
1. 3. 1- к е с т е

0
1
1
0
1. 3. 1- сурет. “Инверсия” логикалық функциясы-ның ақиқат кестесі.
1. 4. “Конъюнкция” (“Және”-”и”) функциясы.
“Және”-”конъюнкция” функциясы (Ү) логикалық айнымалыларды (х 1 , х 2 ) өзара логикалық көбейтуді талап етеді. “Конъюнкция” төмендегі алгебралық өрнектермен анықталады.
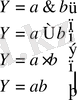 (1. 4. 1)
(1. 4. 1)
“Және”-”конъюнкция” функциясының сызба жобалардағы белгілері:
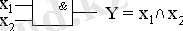 1. 4. 2
1. 4. 2
1. 4. 2 - сурет. “Конъюнкция” функциясының сызба жобадағы шартты белгісі.
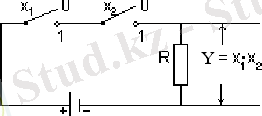
“Конъюнкция” логикалық функциясын айырғыш-қосқыш (вентиль, кран, кілт, т. т. ) қызметін атқаратын функция ретінде пайдалануға болады. “Конъюнкция” логикалық функциясының тағайындайтын амалын, мына төмендегі электр тізбегі арқылы іске асыруға болады.
 1. 4. 3
1. 4. 3
1. 4. 3. - сурет . “Конъюнкция” логикалық функциясы тағайындайтын логикалық амалдарын жүзеге асыру мүмкіндігін түсіндіретін электр тізбегі.
1. 4. 1. - к е с т е
0
0
1
1
0
1
0
1
0
0
0
1
1. 4. 1 - сурет. “Конъюнкция” - логикалық фун-кциясының ақиқат кестесі.
“Және”-”конъюнкция” логикалық функциясы үшін мына төмендегі тепе-теңдіктер - аксиомалар орындалады.
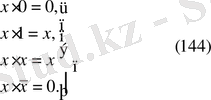
1. 5. “Немесе” - ”Или” - ”Дизъюнкция” логикалық функциясы.
“Немесе”-“дизъюнкция” логикалық функциясы логика - лық айнымалыларды бір бірімен қосуды талап етеді.
Ең болмағанда біреуі логикалық “1” мәнін қабылдайтын логикалық х 1 , х 2 , х 3 . . . айнымалыларына “немесе”-”дизъюн-кция” логикалық функциясы анықтайтын логикалық қосуды, қолданғанда логикалық “1” шығады.
“Немесе”-”дизъюнкция” логикалық функциясының логикалық теңдеулері:

1. 5. 1- к е с т е
0
0
1
1
0
1
0
1
0
1
1
1
1. 5. 1 - сурет. “Немесе” - ”дизъюнкция” логика-лық функциясының ақиқат кестесі.

1. 5. 2 - сурет. “Дизъюнкция” функциясының сызба
жобадағы шартты белгісі.
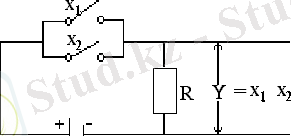
1. 5. 3 - сурет. “Дизъюнкция” логикалық функциясы тағайындайтын логикалық қосу амалын жүзеге асыратын электр тізбегі.
1. 6. “Және - жоққа шығару” - ”шеффер” (”и - не”) логикалық функциясы.
“Шеффер” логикалық функциясы логикалық айнымалыларға “конъюнкция” және “инверсия” логикалық амалдарын бірінен кейін бірін қолдануды талап етеді.
“Шеффер” функциясы логикалық “1” мәнін қабылдау үшін оның логикалық аргументтері барлығы бірдей - бір мезгілде логикалық “1” мәнін қабылдамау керек. Басқаша айтқанда, “шеффер” функциясы “0” мәнін аргументтердің бір ғана комбинациясында, тек барлығы бір мезгілде “1”-ге тең болған- да ғана қабылдайды.
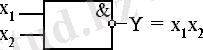
1. 6. 1 - сурет. “Шеффер” функциясының сызба жобадағы шартты белгісі.
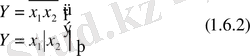
(1. 6. 2) - өрнектерімен “Шеффер” функциясының Буль алгебрасындағы аналитикалық түрі беріледі.
“Шеффер” функциясы ақиқат кестесі.
1. 6. 1-к е с т е
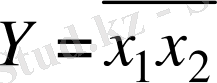
0
0
1
1
0
1
0
1
1
1
1
0
1. 7. “Немесе - жоққа шығару” - ”Пирс” (”или - не”) логикалық функциясы.
“Пирс” функциясы логикалық айнымалыларға “дизъюнк-ция”, “инверсия” логикалық амалдарын бірінен кейін бірін қолдануды талап етеді.
“Пирс” функциясы логикалық “1” мәнін қабылдау үшін оның логикалық аргументтері қатарынан - бір мезгілде логикалық “0” мәнін қабылдаулары керек.
“Пирс” функциясы сызба жобада төмендегі белгілерімен көрсетіледі.
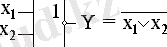
1. 7. 1 - сурет. “Пирс” функциясының сызба жобадағы шартты белгілері.
“Пирс” функциясы Буль алгебрасында
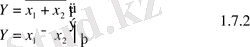
теңдеулерімен анықталады.
“Пирс” функциясы төмендегі ақиқат кестесімен беріледі.
1. 7. 1 - к е с т е
Логикалық
айнымалылар
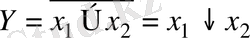
0
0
1
1
0
1
0
1
1
0
0
0
1. 8. “Бірмәнділік” (равнозначность-эквивалентность)
-”Исключающее или-не”, Әрмәнділік”(неравнозначность)
-”Исключающее или” функциялары.
“Дизъюнкция”, “конъюнкция” және “инверсия” қарапай- ым логикалық функциялар жиыны арқылы кезкелген логикалық функцияны құрастыруға болады. Сондықтан, бұл үш қара- пайым логикалық функциялар, толық жиын құрайды.
Мысал ретінде, ЭЕМ-де пайдаланатын біраз логикалық функцияларды, жоғарыдағы үш қарапайым логикалық функциялар арқылы құрастыруға болатындығын көрсетейік.
“Әрмәнділік” логикалық функциясын “2 модуль бойынша қосу” функциясы деп те атайды. Осы “әрмәнділік” функциясын қарастырайық.
“Әрмәнділік” функциясының сызба жобадағы шартты белгісі.
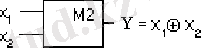
1. 8. 1 - сурет. “Әрмәнділік” логикалық функциясының сызба жобадағы шартты белгісі
Егер х 1 , х 2 логикалық айнымалылары бір мезгілде тең мәндер қабылдаса, яғни х 1 = х 2 болса “әрмәнділік” логикалық функциясы “0”- дік мән қабылдайды, ал егер х 1 ≠ х 2 болса, онда ол “1”- ге тең болады. Бұл функцияны жоғарыдағы қарапайым функциялар арқылы былай құрастыруға болады:
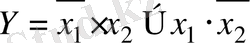 (1. 8. 2)
(1. 8. 2)
“Әрмәнділік” (исключающее “или” ) функциясы мына төмендегі ақиқат кестесі арқылы беріледі.
1. 8. 1 - к е с т е
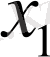
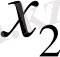
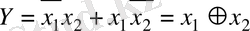
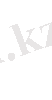
0
0
1
1
0
1
0
1
0
1
1
0
Сонымен, “және” , “немесе”, “жоққа шығару” үш қарапа-йым логикалық функцияларының жиыны толық жиын құрады.
“2 модуль бойынша қосу” логикалық функциясын “және”, “немесе”, “логикалық жоққа шығару” логикалық функциялары арқылы құрастыру мүмкіндіктерін төмендегі сызба жобалардан байқауға болады.
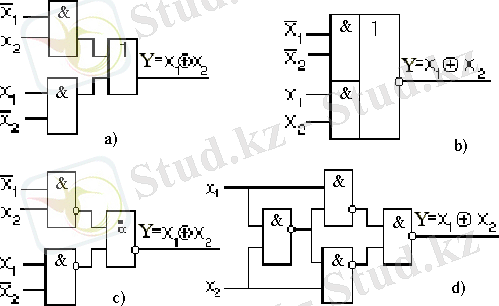
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz