Идеал серпімді қатты денелер. Идеал сұйық динамикасының негізгі заңы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 59 бет
Таңдаулыға:

Мазмұны

І. Кіріспе . . . 2

1. 1. Идеал серпімді қатты денелер . . . 3-4

1. 2. Қатты денелер деформацияларының түрлері және оларды сипаттайтын заңдар . . . 4-7

1. 3. Тепе-теңдік күйдегі сұйық және газ денелер . . . 7-13

1. 4. Сұйықтың стационар ағысы. Ағын сызықтары мен түтіктері. Үздіксіздік теңдеуі . . . 13-15

ІІ. Негізгі бөлім:

2. 1. Идеал сұйық динамикасының негізгі заңы . . . 16-18

2. 2. Бернулли теңдеуі . . . 19-23

2. 3. Ағын жылдамдығын өлшеу әдістері . . . 23-28

2. 4. Сұйықтың тесіктен ағуы . . . 28-31

2. 5. Ағын түтігі қимасындағы қысым өзгеруі . . . 29

2. 6. Үйірілген сұйықтағы қысым үлестірілуі . . . 31-32

2. 7. Ішкі үйкеліс күштері . . . 32-34

2. 8. Құбырдағы тұтқыр сұйық ағысы . . . 35-38

2. 9. Идеал сұйық және газ орталардағы дене қозғалысы . . . 38-42

2. 10. Ұқсастық критерийлері . . . 43-46

2. 11. Шекаралық қабат. Құйындардың пайда болуы . . . 47-49

2. 12. Маңдайлық кедергі және көтергіш күш . . . 50-52

2. 13. Ұшақ қанатының көтергіш күші. Н. Жуковский формуласы . . . 52-55

2. 14. Магнус эффектісі . . . 55-57

2. 15. Тұтқыр ортадағы дене қозғалысын зерттеуге фракталдар теориясын қолдану . . . 57-60

ІІІ. Қорытынды . . . 61

Қосымша . . . 62-71

Пайдаланылған әдебиеттер . . . 72

Кіріспе:

Физика - материя қозғалысының жалпы және қарапайым формаларын, қасиеттерін зерттейтін ғылым. Физика - табиғаттың алуан-түрлі құбылыстары мен тәжірибелерге негізделген ғылым. Сол сияқты физика пәнінің мақсаты - табиғаттың жалпы заңдарын іздеу және солардың негізінде нақтылы процестерді түсіндіру. Физикада анықталған іргелі заңдар өзінің күрделілігі мен орнықтылығы жөнінен кез келген құбылыстарды зерттеу басталатын деректерден әлдеқайда асып түседі.

Алайда олар тікелей бақыланатын қарапайым құбылыстар жөніндегі білімдер сияқты, әрі сенімді және объективті. Бұл заңдар ешқашан да және ешбір жағдайда да бұзылмайды. Механика әртүрлі денелердің қозғалысын зерттеу және сипаттау үшін түрлі модельдерді қолданады. Механика материя қозғалысының ең қарапайым түрі - салыстырмалы орын ауыстыру - туралы ілім болып табылады.

Механиканың даму үрдісі адамзат мәдениеті тарихымен тығыз байланыста. Осы уақытқа дейін сақталған Мысырдағы пирамидалар мен ертедегі құрылыстардың қалдықтары бізді ежелгі халықтарға тепе-теңдіктің негізгі заңдары белгілі болғанын мойындауға мәжбүр етеді, ол заңдарсыз сондай зәулім ғимараттарды салу мүмкіндігі болмас еді.

Кейін зерттеушілер механиканың негізгі заңдылықтарын жалпы түрге келтіріп, күрделі механикалық құбылыстарды талдау әдістерін жетілдірді.

І. Тұтас орта механиканың негіздері.

1. 1 Идеал серпімді қатты денелер.

Реал денені құраушы құрылымдық бөлшектер еш уақытта бұлжымайтын байланыста болмайды, олар бір-біріне қарағанда салыстырмалы қозғалуы мүмкін, сондықтан әрқашан денелердің деформацияға түсу қабілеті сақталады. Бірақ зерттеліп отырған процесте қатар орналасқан бөлшектер (мысалы, атомдар) бірдей қозғалса, біз дененің сирек орналасқан атомдардан құралатынын ескермей, тұтас көлем ретінде қарастыра аламыз. Осындай көзқарастан тұтас орта , немесе тұтас денелер , түсінігі туады. Яғни, реал денені дербес кішкентай элементтерге бөліп, оларға әдеттегі механика заңдарын қолданамыз. Мұндай әдісті тек әрбір элемент саны өте көп құрылымдық бөлшектерден құралғандықтан ғана қолдануға болады.

Қатты денелер деформациясына келсек, оны екі шекті түрге бөлуге болады: серпімді және пластикалық деформациялар. Денеге түсірілген күш әрекеті тоқтағаннан кейін деформация салдары жоғалса, оны серпімді дейді. Ал күш әрекеті тоқтағаннан кейін де ең болмағанда деформацияның аз қалдығы сақталса, оны пластикалық деп атайды.

Егер күш (дәлірек айтқанда, кернеу) серпімділік шегі деп аталатын белгілі шамадан артпаса, пайда болатын деформация серпімді болады. Әрине, дәл айтқанда, күш әрекеті тоқтағанмен, барлық деформациялар қалдықтары толығымен жоғалмайды: бірақ байқалатын қалдықтардың шамасы деформацияның максималды мәнінің 0, 1%-нен артпаса, оларды ескермеуге болады. Механика дененің серпімділік қасиеттерін Юнг модулі сияқты тәжірибе негізінде енгізілген серпімділік тұрақтылар арқылы бейнелейді. Егер дене біртекті болса, әрекет күш үлгі көлденең қимасының бетінде бірқалыпты үлестірілген деп санауға болады.

Орта изотропты және анизотропты болып екіге бөлінеді. Егер дене қасиеттері барлық бағыттарда бірдей болса, оны изотропты дейді. Керісінше, қасиеттер бағытқа тәуелді болса, ондай денені анизотропты деп атайды. Мысалы, анизотропты денелер қатарына кейбір кристалдар жатады. Олардың қасиеттері әр бағытта әр түрлі. Бірақ анизотроптық монокристалдарда байқалады, ал реал кристалдардың көпшілігі - поликристалдар, яғни олар ретсіз бағытталған өте ұсақ кристалдардан құралады. Сондықтан поликристалдарды изотропты деп санауға болады.

1. 2 Қатты денелер деформацияларының түрлері және оларды сипаттайтын заңдар.

Деформацияның негізгі түрлерін анық елестету үшін 1- суретте бейнеленген модельді қолдану қолайлы. Бірнеше бірдей пластиналар (мысалы, фанерден жасалған) төрт бұрыштарынан бірдей серіппелер арқылы қатар-қатар жалғастырылған. Төменгі пластина сол бетіне бекітіледі. Сонда жоғары пластинаны тартсақ, дененің созылуын , ал оны төмен итерсек, дененің сығылуын байқаймыз. Пластиналар арасындағы қашықтық қатар пластиналардың барлық нүктелерінің аралығыда бірдей бола отырып өзгереді. Ығысу деформациясын бақылау үшін жоғарғы пластинаны өз-өзіне параллель қозғалту керек. Бұл кезде пластиналар арасындағы қашықтық өзгерусіз қалады, бірақ көрші пластиналардың бір вертикаль бойында жатқан нүктелері бір-біріне салыстырмалы бір бағытта бірдей қашықтыққа ығысады.

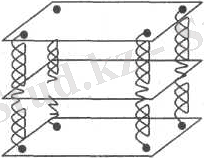
1-сурет

Мұндай деформацияны біртекті ығысу деп атайды. Иілу деформациясын жоғарғы пластинаны көлбеу қозғалтқанда байқауға болады. Мұндай деформация кезінде жақын орналасқан пластиналар аралығындағы қашықтық әр нүктеде әр түрлі өзгереді. Бір жақта қашықтық үлкейсе, оған қарсы жақта кішірейеді. Осыған байланысты иілу деформациясын біртекті емес сығылу, немесе созылу деп қарастыруға болады. Бұралу деформациясы жоғарғы пластинаның вертикаль осьті айналуынан туады.

Созылу немесе сығылу шамасын салыстырмалы ұзару ε сипаттайды. Бұл коэффициенттің мәні сығылу немесе созылуға байланысты теріс немесе оң болады. Ал дененің кез келген бағыттағы созылуы көлденең бағыттағы сығылумен қатар жүреді. Мысалы, вертикаль тұрған резина түтікке сақинаны тығыз кигізіп, түтікті созсақ, оның диаметрі кішірейгендіктен, сақина сырғып түсіп кетеді. Денені сыққанда немесе созғанда оның көлденең өлшемдерінің бұлай өзгеруін мына формула өрнектейді:

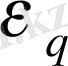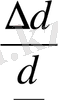= Equation. 3 (1. 1)

мұнда d- дененің деформацияға дейінгі көлденең өлшемі, ∆d- ол өлшемнің деформация кезінде өзгеруі.

Әрине, ε _q мен ε таңбалары бір біріне қарсы екені айқын. Олардың арасындағы

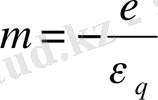(1. 2)

қатысты Пуассон коэффициенті деп атайды. Пуассон коэффициенті дене өлшемдеріне тәуелді емес және бір материалдан жасалған барлық денелер үшін мәні бірдей болады, яғни, заттың меншікті қасиеттерін сипаттайтын тұрақты болады. Созылу және сығылу деформациялары әрқашан дене көлемінің өзгеруіне байланысты. Қырының ұзындығы бірлік өлшем кубтың ұзындығы шамасы аз деформациядан кейін 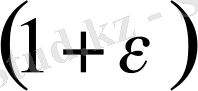және қимасы 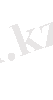(1+ ε _q ) ² ≈ 1+2ε _q болады (ε _q - µте аз болғандықтан) . Ал деформацияға дейін 1-ге тењ V куб көлемі деформациядан кейін

V′ = (1+ ε) (1+ ε _q ) ² ≈ 1+ ε + 2ε _q

болады. Дене көлемнің өзгеруі мынаған тең:

∆ V= V′ - V = ε + 2ε _q = ε (1-2ν), (1. 3)

мұнда

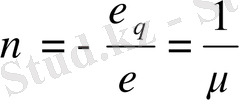
Пуассон коэффициентіне кері шама.

Ығысу деформациясы салыстырмалы ығысу мөлшерімен анықталады. Егер біз дененің түзу сызық бойында жатқан, мысалы, сол жағында орналасқан нүктелерді тиісті әріптермен белгілесек (2-сурет), онда деформация кезінде АА', ВВ', СС' және тағы осы сияқты абсолют тік ығысулар әр нүктелер үшін әр түрлі болады.

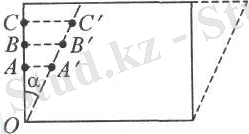
2-сурет

Бірақ осы ығысулардың О нүктесіне дейінгі қашықтыққа қатынастары бірдей екені айқын, яғни

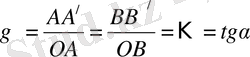(1. 4)

Бұл γ шамаларды салыстырмалы ығысу деп атайды. Егер деформациялар аз болса, tgα ≈ α, яғни γ = α. Біртекті ығысу деформацияларында γ мәні дененің барлық нүктелерінде бірдей. Ығысу деформацияларын дене бетіне жанама күштер тудырады. Жанама кернеулерді τ әрпімен белгілейік. Тәжірибелерге қарағанда бір материал үшін γ мен τ арасындағы байланыс Гук заңындағы ε мен σ арасындағы тәуелділік сияқты, яғни

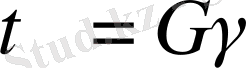(1. 5)

мұнда G - ығысу модулі.

Деформация кезінде деформацияны тудыратын сыртқы күштер жұмыс істейді. Екінші жағынан, деформация жоғалғанда дененің өзі де жұмыс жасайды. Абсолют серпімді денелерде деформациялану барысында істелген жұмыс толығымен серпімді деформацияның потенциалдық энергиясының өсуіне жұмсалады. Сондықтан деформацияланған дененің серпімді деформация энергиясын былай есептеуге болады. Дене элементінің шексіз аз dx орын ауыстыруы кезіндегі істелетін шексіз аз δА жұмысты қарастырайық. Бұл жағдайда әрекет Ғ күшті тұрақты дене деп санауға болады:

Күшті Гук заңын қолдана отырып өрнектейміз:

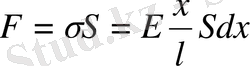
Мұнда Ғ күш дененің S қимасына әрекет жасайды, х қашықтық 0-ден ΔL- ге дейін өзгереді. Бірақ

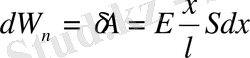
мұнда dW _n - деформацияланған дененің потенциалдық энергиясының шексіз аз өзгеруі. Соңғы теңдеуді интегралдай отырып,

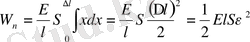
нәтиже аламыз. Бұдан энергия тығыздығы, яғни бірлік көлем энергиясы табылады:

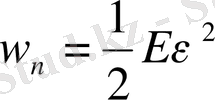(1. 6)

Дәл осындай ығысу кезіндегі серпімді деформация энергиясын есептеуге болады:

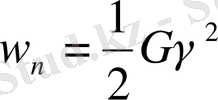(1. 7)

1. 3 Тепе - теңдік күйдегі сұйық және газ денелер

Єрбір ќатты дененіњ µзіндік пішіні мен кµлемі бар екені белгілі. Ќатты дененіњ пішіні мен кµлемін µзгерту ‰шін оѓан белгілі к‰ш т‰сіру ќажет. Сондыќтан денені абсолют ќатты деп санаѓанда (механикалыќ маѓынада) оныњ механикасы материялыќ н‰кте механикасына ауысады. С±йыќтар мен газдар - т±раќты пішіндері жоќ физикалыќ денелер: олар µзін шектен т±рѓан ыдыстыњ пішінін ќабылдайды. Біраќ с±йыќтыњ аныќталѓан µзіндік кµлемі болса, газ єрќашан м‰мкін болатын кµлемді толыѓымен толтырып отырады. Дегенмен, осындай айырмашылыќтарѓа ќарамастан, классикалыќ механика пєнінде жеткілікті дєлдікпен ќатты, с±йыќ жєне газ денелер бірт±тас жєне ‰зіліссіз орта деп ќарастырылады.

Жан-жаѓынан оќшауланѓан ыдыс ішіндегі с±йыќ немесе газ тєрізді ден еге сырттан т±раќты єсер болуы м‰мкін. С±йыќ (газ) поршені бар цилиндр ішінде орналассын делік. Егер поршеньге белгілі Ѓ к‰ш єрекет жасап, оныњ салдарынан поршень мен с±йыќ тепе-тењдік к‰йде болса, б±л-с±йыќ тарапынан поршеньге шамасы тењ, баѓыты ќарама-ќарсы Ѓ' к‰ш єрекет етуініњ белгісі. Поршеньге тікелей т‰йісіп т±рѓан с±йыќ кµлемі бір бµлігініњ тепе-тењдік шартынан оѓан с±йыќтыњ басќа бµліктерініњ к‰ш т‰сетінін, яѓни с±йыќ ортада да ќатты денедегі сияќты ішкі кернеулер туатыны, байќалады.

С±йыќ немесе газ ортада пайда болатын уаќыт бойынша т±раќты (статикалыќ) кернеулердіњ ќатты денелердегі кернеулерден т‰бегейлі айырмашылыѓы - олардыњ жанама ќ±раушыларыныњ болмауында. С±йыќ немесе газдаѓы статикалыќ ішкі к‰штер бµліп алѓан кез келген кµлемніњ беттеріне єрќашан нормаль болады. Міне, сондыќтан с±йыќтар мен газдарда тыныштыќ ‰йкелісі нольге тењ. Сонымен, дене с±йыќ бетінде ќалќып ж‰рсе, горизонталь баѓытта єрекет еткен кез - келген к‰ш ќозѓалыс тудырады. Осындай ќасиет газ ортаѓа да тєн. С±йыќтар мен газдардаѓы кернеуді ќысым деп атайды.

Ќысым-бµліп алынѓан кµлемді шектеп т±рѓан бетті бірлік ауданына нормаль баѓытта єрекет жасайтын к‰ш. Ќысым єдетте р єрпімен белгіленіп, ХБЖ-де µлшемі паскаль деп аталады: [р] = Па= 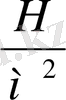. Ќысымныњ ж‰йеден тыс µлшемдері де бар: физикалыќ атмосфера (атм), техникалыќ атмосфера (ат), синап баѓанасыныњ миллиметрі немесе сантиметрі деп аталатын, олардыњ арсында мынадай

1 атм = 760 с. б. мм = 1, 033ат=1, 013*10 ⁵ Н/м ²

байланыс бар. С±йыќ пен газ орталар тепе-тењдік к‰йде болѓанда Паскаль зањына баѓынады. Тыныштыќтаѓа с±йыќ немесе газ кµлемдегі ќысым барлыќ баѓытта бірдей жєне ќысым с±йыќ алып т±рѓан барлыќ кµлемде бірдей таратылады.

С±йыќтыњ тыѓыздыѓы ќысымѓа айтарлыќтай тєуелді емес. Мысалы, су ортаѓа т‰сірілген ќысым 1000 атм-ѓа µскенде оныњ кµлемі тек 5% -ке µзгереді. Сондыќтан гидростатикада кµлемніњ µзгеруін ескермейді, яѓни с±йыќ сыѓылмайды деп саналады. Ал, газдарѓа келсек, олардыњ тыѓыздыѓы ќысымѓа айќын тєуелді. Физиканыњ мектеп курсынан белгілі болѓандай, идеал газ ортада ќысым мен тыѓыздыќ арасындаѓы байланыс Менделеев - Клапейрон зањымен µрнектеледі.

Жоѓарыда Паскаль зањыныњ т±жырымдамасын келтіргенде біз с±йыќтыњ (газдыњ) салмаѓын ескермедік. Енді тыныштыќтаѓы сыѓылмайтын с±йыќ ортада ќысымныњ таратылуына с±йыќ салмаѓыныњ єсерін есептейік. Горизонталь баѓытта ќысым ‰немі бірдей болатыны аќиќат, себебі басќаша болса, тепе-тењдік к‰й ќалыптаспас еді. Ал, вертикаль баѓытта ќысым, орта мектептегі физикада айтылѓандай, биіктікке (терењдікке) байланысты.

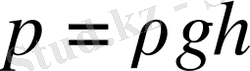(1. 8)

зањына сєйкес µзгереді. М±нда ρ - с±йыќ тыѓыздыѓы, g - еркін т‰су ‰деуі, h - биіктік. (1. 8) формуламен аныќталатын ќысымды гидростатикалыќ деп атайды.

Газ ортада ќысым кез келген горизонталь жазыќтыќта бірдей. Біраќ вертикаль баѓытта ќысымныњ µзгеруін аныќтау ‰шін тыѓыздыќтыњ ќысымѓа тєуелділігін ескеру ќажет (3 -сурет) .

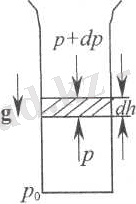
3-сурет

Шынында, табан ауданы бірлік µлшем, биіктігі dh элементар цилиндрлік кµлемніњ тепе-тењдігін былай µрнектеуге болады:

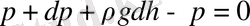
м±нда dp -цилиндрлік кµлемніњ жоѓарѓы жєне тµменгі табандарыныњ арасындаѓы ќысым айырымы, яѓни

(1. 9)

алынѓан тењдікті интегралдап, ќысымныњ мєнін аныќтау ‰шін, тыѓыздыќтыњ ќысымѓа тєуелділігі белгілі болу керек. Ол ‰шін мысал ретінде газ температурасы т±раќты деп алсаќ, белгілі Бойль-Мариотт зањын ќолдануѓа болады:

pV = const немесе pV = p ₀ V ₀

б±дан V = m/ρ жєне m = const екенін ескере отырып,

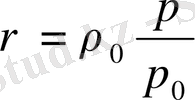
осы мєнді (1. 9) тењдеуге ќойып, интегралдасаќ, мынадай нєтиже аламыз:

ln p _h - ln p ₀ = - ρ ₀ gh/p ₀

м±нда p ₀ - ыдыс т‰біндегі, p _h - газдыњ биіктігіндегі ќысым.

Енді логарифмдік функциядан кµрсеткіштік функцияѓа ауысып, ќорытынды шешімге келеміз:

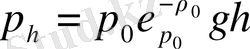(1. 10)

Б±л, єлбетте, ќысымныњ биіктік бойынша кµрсеткіштік зањымен µзгеруін бейнелейтін барометрлік формула. Біраќ к‰нделікті ќолданылып ж‰рген ќысымдар аралыѓында (1. 10) формула орнына одан ќарапайымдау зањдылыќ жиірек ќолданылады. Ол ‰шін (1. 10) -ніњ оњ жаѓын ќатарѓа жіктеп, жіктеудіњ тек алѓашќы екі м‰шесін ќалдырамыз:

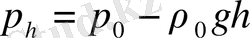(1. 11)

Есептеулерге ќараѓанда (1. 11) жуыќ формуланы 8км-ден біршама тµмен биіктіктер ‰шін ќолдануѓа болады (есептеулер тењіз дењгейіндегі температурасы 15 ⁰ С Жер атмосферасы ‰шін ж‰ргізілген) .

С±йыќќа (газѓа) толыќ немесе бір бµлігі батырылѓан денеге орта тарапынан к‰ш єрекет ететіні белгілі. Б±л ќ±былысты Архимед (б. э. д ІІІѓ) зерттеп, табылѓан зањѓа оныњ аты беріліп еді: с±йыќќа немесе газѓа батырлѓан кез келген денеге ќоршап т±рѓан орта тарапынан шамасы ыѓыстырылѓан с±йыќ (газ) салмаѓына тењ к‰ш єрекет етеді. Б±л к‰ш жоѓары баѓытталып, ыѓыстырылѓан с±йыќ (газ) массалар центрі арќылы µтеді. М±ндай к‰штіњ болуы жєне оныњ шамасы салмаѓы бар с±йыќќа ќысымныњ таратылуымен кµрнекті т‰рде т‰сіндіріледі. Архимед зањын дєлелдеу ‰шін кµз алдымызѓа ќимасы кішкентай, жасаушылары вертикаль циліндр кµлемдерден ќ±ралѓан денені с±йыќ ортада елестетіп, сол єрбір циліндрден егер єрекет еткен күшті аныќтап, аќырында барлыќ цилиндр бµліктерге єрекет жасаѓан к‰штердіњ тењ єрекетті к‰шін есептеу ќажет. Егер с±йыќ ортаѓа дененіњ тек бір бµлігі батып т±рса, есептеу барысы б±рынѓыша ќалып, цилиндр ќ±раушыларѓа дененіњ батќан бµлігі бµлінеді. С±йыќ бетінде ќалќып ж‰рген дененіњ салмаѓы ол ыѓыстырѓан с±йыќ кµлемініњ салмаѓына тењ. Егер ќалќыѓан дененіњ ауырлыќ центрі ыѓысќан с±йыќ кµлемініњ ауырлыќ центрінен тµмен болса, дене орныќты тепе-тењдік к‰йде болатыны айќын. Біраќ орныќты тепе-тењдік к‰й к‰нделікті µмірде, мысалы, су бетінде кемелер ж‰зген кездегідей, дененіњ ауырлыќ центрі ыѓысќан с±йыќ кµлемініњ ауырлыќ центрінен жоѓары жатќан жаѓдайда да орын алады. Мысал ретінде пішіні тікб±рышты параллелепипед аѓаш кесектіњ су бетінде ќалќуын ќарастырайыќ (4 -сурет) кесек орныќты ж‰зеді. Ал егер кесекті басќа жаѓдайда (4б-сурет) ж‰зуге жіберсе, ол аударылып, біршама тербелістерден кейін орныќты к‰йге келеді.

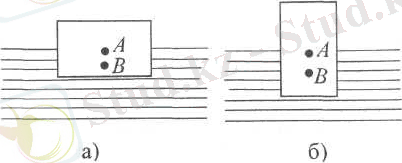
4-сурет

Кµлемі ќысымѓа тєуелді емес дене не с±йыќ бетінде ќалќып ж‰реді, не ыдыс т‰біне батады. Егер дене салмаѓы ыѓысќан с±йыќ кµлемініњ салмаѓына дєл тењ болса, ол с±йыќтыњ кез келген бµлігінде талѓаусыз тепе-тењдік к‰йде болады. Мысалы, тауыќ ж±мыртќасын су ќ±йылѓан мµлдір шыны ыдысќа тастап, суда т±зды бірте-бірте ерте отырып, ж±мыртќаны кез келген терењдікте ±стап т±руѓа болады. Б±л кезде ж±мыртќаныњ ауырлыќ центрі ыѓысќан су кµлемініњ ауырлыќ центрінен тµмен орналасып, екеуі де вертикаль бойында жатады. Егер ж±мыртќаны б±л к‰йден шыѓарып жіберсе, ол µзінен-µзі байта айналып орныќты жайына келеді.

Енді “картезиан с‰њгуірі” деген атпен кењінен белгілі аспапты мысал ретінде негізге ала отырып, ќысым µскенде кµлемі азаятын дененіњ тепе-тењдік к‰йін ќарастырайыќ (5-сурет) . Су толтырылып, серпімді жарѓаќпен жабылѓан биік шыны ыдыс ішінде ж‰к бекітілген ашып аузы тµмен аударылѓан шыны т‰тік ќалтќы орналасќан.

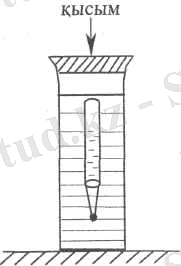
5-сурет

Ќалтќыныњ жоѓары бµлігін ауа, тµменгі бµлігін су толтырѓан. Серпімді жарѓаќты бармаќпен басќанда су баѓаныныњ ‰стінде, соѓан байланысты, су ішінде де ќысым артады: ќалтќыдаѓы ауа сыѓылып, шыны т‰тік ыѓыстырѓан су кµлемі кішірейгендіктен, ќалтќы ыдыс т‰біне т‰седі. Жарѓаќќа т‰сірілген ќысымды азайта отырып, ќалтќыны алѓашќы жаѓдайына келтіре аламыз. Жалпы жарѓаќќа т‰скен күшті реттей отырып, ќалтќыны ойѓа келгендей ќозѓалтуѓа болады. Осындай м‰мкіншіліктіњ арќасында ќарастырып отырѓан тєжірибе негізінде ќызѓылыќты єрі маѓыналы ойыншыќ жасауѓа болады.

Газ ортада ќалќыѓан дененіњ тепе-тењдік шарттары с±йыќтаѓы шарттармен бірдей. Егер газ ортада ќалќып ж‰рген дененіњ кµлемі ќысымѓа тєуелді болмаса, оныњ тепе-тењдік к‰йі ‰немі орныќты болады. Егер дене кµлемі ќысымѓа тєуелді болса, оныњ тепе-тењдік к‰йініњ орныќтылыѓын аныќтау біршама ќиынѓа т‰седі. М±ндай есепте тек дене кµлемініњ µзгеруін де ескеруге тура келеді.

1. 4 С±йыќтыњ стационар аѓысы. Аѓын сызыќтары мен т‰тіктері. ‡здіксіздік тењдеуі.

С±йыќ немесе газ ќозѓалѓанда (аќќанда) кµлем ішінде ішкі ‰йкеліс, яѓни т±тќырлыќ к‰штері, пайда болады. Б±ѓан ќоса с±йыќќа азыраќ, газға кµбірек дењгейде сыѓылушылыќ ќасиет тєн. Біз әуелі идеал с±йыќ (газ) ортаныњ стационар аѓысын ќарастырамыз.

Идеал газ (с±йыќ) деп зерттеліп отырѓан мєселеніњ шарттарына сєйкес т±тќырлыѓын ескермеуге болатын ортаны айтады.

Єрине, табиѓатта м±ндай газ немесе с±йыќ жоќ. Біраќ кµптеген ќолданбалы мањызы бар жаѓдайларда газ немесе с±йыќ ортаныњ, немесе ќатты денелердіњ с±йыќ (газ) ортадаѓы ќозѓалысын осылай идеал т‰рде елестету жаќсы нєтижелер береді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.