Турбуленттік сорғының кеңею қарқындылығының коэффициентін тәжірибе арқылы анықтау

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 40 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... .5

1. Гетерогендік сұйықтың турбулентті ағысындағы

когеренттік құрылымдар, фрактальді кластерлер және
мультифрактальді
объектілер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ...5
2. Турбуленттік сорғының кеңею қарқындылығының

коэффициентін тәжірибе арқылы
анықтау ... ... ... ... ... ... ... ... ... ... ... ... ... ...14
3. Газдың жалынындағы және ауаның құйындық
ағыстарындағы кластерлердің әрекеттесуін
зерттеу ... ... ... ... ... ... ... ... ... ..21
4. Турбуленттіліктің өзұйым деңгейінің ақпараттық
сипаты ... ... ... ... ... ... ... . 28
5. Біртекті турбуленттіліктің пульсацияларының

энтропиямен
байланысы ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... .34
6. Турбуленттіліктегі өзұйым дәрежелі сипаттарының
мәнін тәжірибе жүзінде
тексеру ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
...41

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ...48

ҚОЛДАНЫЛҒАН
ӘДЕБИЕТТЕР ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... 49

Аңдатпа
Турбулентті ағыстың теориясы Г.Н. Абрамович, Бай-Ши-и, Л.А Вулис,
В.П. Кашкаров, А.С. Гиневский еңбектерінде кеңінен қарастырылған.
Сорғыда ағатын ағымдары тұрақсыз екендігі белгілі болғандықтан, іс жүзінде
ағыс канал кесіндісіне жақындағанда ғана ламинарлы, ал каналдан едәуір
алшақтағанда турбулентті болады. Нақты уақытта еркін ағыстар мен
шырақтардағы тұрақсыздық аймақтарының қалыптасуына тәжірибелік және
теориялық зерттеу жұмыстардың айтарлықтай саны орындалған. Бірақ, бойында
турбуленттік сипаттамаларды анықтауға мүмкіндік беретін негізгі үрдістердің
сапалы сипаттамаларын ғана емес, сонымен бірге сандық ара қатынасынан
тұратын турбуленттіліктің жалпы теориясы әлі қалыптаспаған.
Қазіргі кезде турбулентті ағыстардың қасиеттерін зерттеуде
фракталдар теориясының қолданылуына байланысты сорғыда ағатын ағымдардың
шекарасына теориялық есептеулер жүргізуге мүмкіндік туды. Ағыстағы
турбуленттілік оның шекарасының қабатында пайда болатын когеренттік
құрылымдарды күйрету арқылы дамиды.
Осы құрылымдар Жанабаева З.Ж., Мухамедин С.М. жұмыстарында
фрактальді кластерлер сияқты - өзіне тән иерархиялық макроскопиялық
құрылымдар болып ұсынылды.

Annotation
The theory of turbulent flow is widely researched in studies of G.N.
Abramovich, Bay-Shi-i, L.A. Vulis, V.P. Kashkarov, A.S.Ginevskiy. It is
known that the streams flowing in a pump are not constant; in practice flow
is laminar when it is closer to cross-section of a pipe and turbulent when
it is closer to walls. Several theoretical and practical studies are made
in order to find out the instant obtaining of variable regions of sources
and flows. However the ways to explain characteristic properties of
descriptions containing turbulent flows and general theory of relations
between numerical values in turbulent flows are not formed yet.
Nowadays with the possibility to apply the fractal theory in research
of properties of turbulent flows appeared the possibility to make
theoretical calculations to the boundary of flows in a pump. The turbulence
in flows develops through the breaking down coherent forming obtained in
layers on its boundary.
These forms are suggested as hierarchical macroscopic forms like
fractal clusters in studies of Zhanabayeva Z.Z. and Mukhamedin S.M.

КІРІСПЕ

Сорғыда аққан ағымдардың зерттелуіне эксперименттік, сонымен қатар
теориялық жұмыстардың кең бөлімі арналған. Сорғыда ағатын ағымдарға
білдірілетін қызығушылық техниканың әр түрлі салаларына қажеттілігімен,
маңыздылығымен түсіндіріледі.
Олардың тіптен бар екендігі, әрі олардың жұмыс үрдісінің қарқындатуда
(мысалы, турбулентті араласу үрдісін қарқындату үшін дүрсіл үрдісіндегі ауа
мен газ тәрізді отын ағымы) немесе оның үнемділігін арттыруда шешуші рөл
атқаратындығы рас.
Сонымен қатар, ағымдарды зерттеу турбуленттіліктің пайда болу
мәселелерін зерттеу аймағында жалпыфизикалық қызығушылық танытады.
Турбулентті ағыстың ең көп зерттелген түрі басымды ағым болып табылады.
Қоршаған ортаның бөлшектерінен және ағыстың өзінің тежелген бөлшектерінен
тұратын ағымның шекаралық қабатының қалыңдауы, бір жағынан көлденең
қимасының кеңеюіне, ал екінші жағынан, ағыстың потенциалдық ядросының
бірте – бірте қысқаруына әкеледі.
Турбулентті ағыстың кеңею қарқындылық коэфициентінің эмпирикалық мәні
Абрамович Г.Н. және тағы да басқалардың жұмыстарында анықталған кезде
турбулентті ағыстың шекаралық қабатының кеңеюі соңғы уақытқа дейін
теориялық анализге берілмеді.
Қазіргі кезде турбулентті ағыстардың қасиеттерін зерттеуде фракталдар
теориясының қолданылуына байланысты сорғыда ағатын ағымдардың шекарасына
теориялық есептеулер жүргізуге мүмкіндік туды. Ағыстағы турбуленттілік
оның шекарасының қабатында пайда болатын когеренттік құрылымдарды күйрету
арқылы дамиды.
Осы құрылымдар Жанабаева З.Ж., Мухамедин С.М. жұмыстарында фрактальді
кластерлер сияқты - өзіне тән иерархиялық макроскопиялық құрылымдар болып
ұсынылды.
Өзектілігі: Әр түрлі құрылымдардың қалыптасуы когерентті құйындар,
бір және көп фазалы сұйықтықтың сорғыда ағатын ағынындағы фракталды
кластерлер мен мультифракталды объектілері түрінде турбуленттілік
құбылыстармен байланысты. Турбуленттілікті зерттеу ғылыми негізде ғана
емес, сонымен қатар тәжірибелік, әсіресе импульсті көбейту кезінде
гетерогенді сұйықта ағып өтетін нақты үрдістерді зерттеуде маңызы аса зор
болып табылады.
Проектілік жұмыстың мақсаты: Турбуленттік құрылымдардың фракталдық
және мультифракталдық сипаттарының бар екендігін көрсету.
Жұмыстың міндеті:
1. Турбулентті сорғының негізгі бөлігіндегі құйындардың геометриялық
сипаттарын зерттеу;
2. Турбулентті сорғының негізгі бөлігіндегі құйындардың фракталдық және
мультифракталдық қасиеттерін зерттеу.

1. Гетерогендік сұйықтың турбулентті ағысындағы когеренттік
құрылымдар, фрактальді кластерлер және мультифрактальді
объектілер.
Когеренттік құрылымдардың түсінігі өткен жүз жылдықтың жетпісінші
жылдары енгізілген болатын. Когерентті құрылымдар деп ағым бойымен төмен
қарай орналасқан біршама ара қашықтықта когерентті бола тұрып,
қайталанылатын құрылымы бар ірі құйындарды атайды. Когерентті құрылымдар
гидродинамикалық ағымдардың әр түрлі үлгілерінде бар, мысалы турбулентті
бос симметриялы осьтік ағыстарда, гетерогендік сұйықтың газды факелдарында
және турбулентті ағымдарында.
U0 бастапқы жылдамдығы мен соңғы D диаметрлі каналдан қозғалыссыз
кеңістікке ағып тұрған сұйықтың немесе газдың қозғалысы – еркін ағыстар деп
аталатындығы белгілі. Рейнольдстің (Re 50) аз сандары мәнінде сұйықтың
қозғалысы іс жүзінде ағымның барлық көлемінде ламинарлы болып келеді [1].
Бастапқы жылдамдықтың және каналдардың артуымен еркін ламинарлы ағыс
тұрақсыз болады және Re 50 кезінде каналдан белгілі бір қашықтыққа
алшақтағаннан кейін турбулентті қозғалыс дамиды. Re 104 кезінде сұйықтың
қозғалысы ағымның барлық көлемінде турбулентті болады деп есептеу
қабылданған.
Ағым жылдамдықтарының соқтығысу орны үлкеннен ең аз мәндеріне дейін
болған кезде Re үлкен сандарында жалпы қабылданулар бойынша турбуленттілік
түсінігі әр түрлі өлшемді құйындардың иерархиясы деп қалыптасқан.
Жылдамдығының өзгеруіне байланысты өлшемдері мен сипаттамалары
өзгеретін турбуленттік ағыстың ламинарлы ағыстан айырмашылығы бастапқы
жылдамдықтың ауқымды диапазонында автомодельді болып қалады, яғни өлшемсіз
жылдамдықтары және бастапқы орнының ұзындығы, бұрышының ашылуы өз мәндерін
сақтайды.
Турбулентті ағыстың теориясы Г.Н. Абрамович, Бай-Ши-и, Л.А Вулис,
В.П. Кашкаров, А.С. Гиневский еңбектерінде кеңінен қарастырылған [2,3,4,5].
Сорғыда ағатын ағымдары тұрақсыз екендігі белгілі болғандықтан, іс
жүзінде ағыс канал кесіндісіне жақындағанда ғана ламинарлы, ал каналдан
едәуір алшақтағанда турбулентті болады.
Нақты уақытта еркін ағыстар мен шырақтардағы тұрақсыздық
аймақтарының қалыптасуына тәжірибелік және теориялық зерттеу жұмыстардың
айтарлықтай саны орындалған [6-25]. Бірақ, бойында турбуленттік
сипаттамаларды анықтауға мүмкіндік беретін негізгі үрдістердің сапалы
сипаттамаларын ғана емес, сонымен бірге сандық ара қатынасынан тұратын
турбуленттіліктің жалпы теориясы әлі

қалыптаспаған.
Математикалық мәндегі қатаң теорияның құрылуы, турбуленттіліктің
өзіне сипаттама беру жеткілікіті түрде қиындатылған. Дәл осылай [26] – да
келесідей төрт маңызды ерекшеліктер берілген: микроскопиялық, тепе-
теңділіксіз, еркін макроскопиялық деңгейлерінің үлкен сандарының болуы,
ағыс құрылымының күрделілігі. [27] жұмысында турбулентті ағымдардың
жүйеліліксіз (кездейсоқтық), диффузиялық, құйындатылуының үш өлшемді
флуктуациясы, диссипативтік, континуальдық сияқты сипаттамалары
ерекшеленеді.
Турбуленттік қасиеттерінің аса кеңейтілген жүйесі [28] – де берілген:
турбуленттілік тепе-теңділіксіз, стохастикалық, квазистационарлық, ұжымдық,
өзара келісімді, иерархиялық және диссипативтік қасиеттеріне ие.
Тепе-теңділіксіз – аса құйындатылған қозғалыстың және құйындының беткі
қабатындағы әртекті сипаттамаларының ауытқуы кезінде, стохастикалық – ішкі
құрылымдарының кенеттен пайда болуынан, ұжымдық – фрактальді және
мультифрактальді құрылымдардың қалыптасуымен, өзара келісімді – динамикалық
шамаларының (жылдамдық, қысым, құйындық) өзара келісілген өрісімен,
иерархиялық – индуцияланатын құйындардың өзіне тән ұқсастығымен,
диссипативтілік – аса құйындатылуда үзілу пайда болған кезіндегі тұтқырлық
рөлімен байқалады.
[29-32] жұмыстарында жылдамдықтың бастапқы профилі және еркін
ағыстардағы Re санының ауқымды диапазонында турбуленттіліктің табиғи даму
үрдістері, сонымен қатар олардың өтпелі аймағында пульсациялық
энергияларының ең үлкен үлесінен тұратын құйындардың пайда болу жиілігіне
ықпалы зерттелген болатын. Қалыңдығы жұқа шекаралық қабатты симметриялы
осьті ағыстардың бастапқы аймақ жылдамдығының пульсациясындағы
спектрлерінде каналдан шығу қимасында екі түрлі сипаттағы жиіліктер
болатындығы тәжірибе жүзінде дәлелденген.
Бірінші жиілік канал жиегіне жақын үзілген шекаралық қабатындағы ағыс
шекарасында, ал екіншісі – бастапқы аймақтың шетіндегі ағыс осінде
қалыптасады. f0,5 бірінші жиілік еркін ламинарлы шекаралық қабатының
тұрақтылығын жоғалту нәтижесінде периодты ауытқуының пайда болуына себепші
болса, ал f0 екінші жиілік – масштабы бастапқы аймақтағы ағыс диаметрімен
қатарлас үлкен энергия мөлшерлі құйындардың (когерентті құрылымдар)
қалыптасуы арқылы болады. f0,5 бірінші жиілік бойынша есептелінген Sh0,5
Струхаль саны Re санынан алынған квадраттың түбіріне пропорционалды
өзгереді. f0 екінші жиілікке есептелінген Sh0 шамасы Re санына тәуелсіз
және шамамен мынадай тұрақты мәнін сақтайды: Sh0 =0,5 ± 0,1.
Сорғыда ағатын ағымдардың негізгі ерекшелігі араласу қабатында үлкен
масштабты құйындардың (когерентті құрылымдардың) қалыптасуларының болуы
[33]. Едәуір сезімтал аймағындағы ағыс жиілігімен осындай түрдегі ағысқа
[34-36] периодты түрде әсер ету ағынның үлкен масштабты құрылымынан
когерентті құрылымдардың резонансты артуына және кеңсызықты
турбуленттілікке әсер етуіне дейін тиімді басқаруға мүмкіндік береді. Егер
де араласу қабатының қозуы берілген шарттарда мүмкін болатын f0 жиіліктің
төңірегінде жатқан жиілікте [37, 38] орындалатын болса, онда дәл осы
жиілікте когерентті құрылымдар резонансты түрде артып отырады.
Импактылық ағыста үлкен масштабты бірлескен құрылымдар резонансының
артуымен қоздырылған стохастикалық турбулентті соқтығысуларына басымшылдық
жасау эффектісі, сонымен қатар осы құрылымдардың ұсақдисперсиялы газ
фазасымен газға қанағаттыру шарттарында басымшылдық жасау эффектісі осындай
әдіспен [33] жұмысында белгіленген.
[33] пен [34-36] жұмыстарында алынған нәтижелердің анализі газға
қанағатталған импакт ағысында, ауаның изотермиялық симметриялы осьті
толтырылған ағысында және газды шырақтың жалынында құйынды құрылымдардың
(фрактальді кластерлердің) қалыптасу үртістерінің ұқсастығын көрсетеді.
Сонымен бірге қарастырылған зерттеулерде құйынды құрылымдарды басқару
әдістері де ұқсас болып табылады. Сондықтан құйындар мен олардың
кластерлерінің қалыптасуын оның тұйықсыз және үзіліссіз болуы нәтижесінде
сызықтық емес ортаның өзіндік қалыптасуының әмбебаб үрдісі деп қарастырған
дұрыс [39].
Турбуленттіліктің пайда болуы флуктуациялармен байланысты. Үлкен
масштабты – гидродинамикалық флуктуацияларды ламинарлы қозғалыстарда
ескермеуге болғанымен, турбулентті ағындарда көп жағдайларда белгілі бір
рөл атқарады. Гидродинамикалық флуктуацияларды есептеу үшін басқа
әдістермен қатар Ланжевен әдісі қолданылады. Ланжевен негіздерінің теңдігін
орнату жағдайлары үшін гидродинамика теңдіктеріне алғаш рет Л.Д. Ландау
және Е.М. Лившиц енгізген болатын [40]. Л.Д. Ландау гипотезасына сәйкес
турбуленттілік жылдамдықтар мен координаталардың фазалық кеңістігінде
шексіз тор бойымен қозғалысына сәйкес және әр түрлі жиіліктері болатын
периодты тербелістердің үлкен жиынтығы түрінде ұсынылған.
Турбулентті режимге өтудің өзгеше жолын Д. Рюэль мен Ф. Такенс
ұсынды, олар қозғалыстың фазалық кеңістігіндегі тордың бифуркация (екіге
бөліну) үрдісін зерттеді [41, 42]. Жалпы түрде математикалық көзқарас
бойынша бұл мәселе мынадай теңдіктермен сипатталатын детерминирленген
диссипативті жүйелердің эволюциясының анализіне әкеледі:

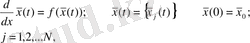(1)

немесе дискретті уақытпен өрнектеледі:

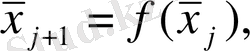(2)

мұндағы – N өлшемді вектор, ол жүйенің жағдайын сипаттайды, –
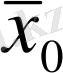бастапқы жағдай. 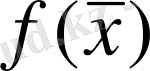функциясында жүйенің жағдайының өзгеруіне әкелетін
және сыртқы байланыстарды білдіретін басқару параметрлері болады. Әдетте
диссипативті жүйенің әрекеті ұзақ уақыт аралығында қарастырылады. Осындай
жүйе траекторияның соңғы көлемінде аттракторға – фазалық кеңістікте
көпшіліктің ықшамына, (1) немесе (2) инвариантқа қатысты сәйкеседі [41].
Оғаш аттракторлар құрылымдылығымен, өзіне тән болуымен, фрактальді
өлшемділігімен сипатталады, яғни фрактальдардың негізгі қасиеттеріне ие.
Турбуленттіліктің пайда болуының бір көрінісі ретінде периодтың еке
еселенген бифуркациясының көп рет қайталануын қарастыруға болады. М.
Фейгенбауммен ұсынылған теория [43, 44] бифуркациялардың бірінен кейін
бірінің тез жүруі соншалықты, олардың тізбектілігі бір параметрге тәуелді
болатын Пуанкаре өрнегімен сипатталады:

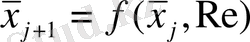
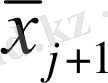– Пуанкаренің бірөлшемді өрнектелуі деп атайды, мұндағы Re –
Рейнольдс саны, 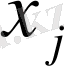– фазалық траекторияның қиылысу нүктесі, –
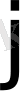қозғалыс периодының бірліктерімен өлшенетін дискретті ауыспалылық.
М.Фейгенбаум көрінісіндегі жылулық конвекция, сызықты емес электр сызбасы
химиялық реакциялармен және т.б. тәжірибелерімен дәлелденген болатын [45,
46].
Араластыру арқылы турбулентті жағдайға өту сипаттамасы күрделі
болады. Кейбір авторлардың классификациясы бойынша араластырулардан
турбулентті тәртібіне өтудің үш түрі бар. Бұл көріністе турбуленттіліктің
пайда болу табиғаты және оның бастапқы жүру жолы жайындағы сұрақтарға
жауап берілмегеніне қарамастан, оның әмбебабтылығы көптеген тәжірибелерді
өткізуімен дәлелденді [45, 46].
[47] жұмыста жаңа тәжірибелік ұсынулардың негізінде дәлелденген
физикалық табиғаты әр түрлі өрістің және электромагниттік өрістің құйынды
сипаттамасының ықпалы мен өзара байланысы турбуленттіліктің бастапқы
деңгейінің гидродинамикалық ағындағы ортаның құйынды қозғалысының
ештеңеден пайда болу механизмі мен себептеріне түсінік беріледі.
Осыдан құйынды қалыптасу үрдісі мен турбуленттіліктің эволюция көрінісін
сипаттайтын теңдеулер алынған.
Құйындардың пайда болу мәселелерін шешу физикалық құбылыстардың екі
өрісті сипаттамаларына негізделген. Берілген жағдайда мұндай өрістердің
бірі электромагниттік (ЭМ), және екіншісі – ортаның ағыны –
гидродинамикалық (ГД) өріс болып табылады. Сонымен бірге, элементар
бөлшектер, атомдар, молекулалар және т.б. қалыптасулар, жартылай немесе
толығымен ЭМ табиғатының физикалық материясынан құралған, яғни ЭМ өрісін
құрайтын материядан тұрады. Бұл жағдайда гидродинамикалық ағынды құрайтын
молекула атомдарының және т.с.с. ортаның макроскопиялық бөлшектерінің
әртекті түрлерінің бірігуі ЭМ өрісімен жалпы материялық негізін бере алады,
қарапайым көзқарас бойынша ол арқылы әртекті физикалық қасиетіне ие ГД
және ЭМ өрістерінің өзара байланысы мен әсері жүзеге асырылуы мүмкін.
Осылайша, мазмұндалған ұстанымдардан гидродинамикалық құйындардың пайда
болуының алғашқы себебі ЭМ мен ГД арасындағы байланыс пен ЭМ материяның
ортаның қозғалысына деген құйынды әрекеттің реакциясы болып табылады деп
ұйғарылған. Нақты ағындарда басқа түрдегі ЭМ өрістері де болуы мүмкін,
мысалы, қабаттарының қозғалысына қатысты қабырғаға үйкелісі және басқа да
себептері нәтижесінде ортаның электрленуі, бірақ бұл жағдай мұндағы сұрақта
қарастырылатын өрістің жеке күштеріне әсер етпейді.
Табиғи шарттарда сұйықтың құрамында әрқашан газ көпіршіктері және
ұсақ қатты бөлшектер болады. Жалпы жағдайда, көбінесе техникалық шарттарда,
қоспалар өлшемдері молекулаға қарағанда едәуір үлкен макроскопиялық
объектілер болып табылады, сондықтан сұйықты гетерогенді немесе көп фазалы
орта ретінде қарастыру керек. Көп фазалы сұйықтың қозғалысы әдетте,
турбулентті.
Сұйық ағынының құрамында болатын ұсақ қатты бөлшектер, газды
көпіршіктер жеке орындарда кейбір фрактальді объектілерді қалыптастыра
отырып жинақталады және кластерленеді. Сұйықтың стационар ағынында
кластеризация үрдісі оған балансталған құлдырау үрдісімен және
құрылымдардың каскадты бөлінуімен жүреді.
Ұсақ қатты бөлшектердің кластеризациясы тәжірибе және есептеулер
жүзінде жақсы зерттелген. Агрегацияның шектелген диффузиясының есептік
модельдену үрдісінің алгоритмі жасалды. Электронды микроскоптың көмегімен
коллоидты бөлшектердің кластерлерінің суреттері алынған, кластерлерді
зерттеу нәтижелері кеңістіктік масштабпен суреттелген, үш реттілікпен
ерекшелінетін (10–6–10–3 мм интервалында), 1,74-тен 2,56-ға [48]
дейінгі 1-сурет, 2-сурет D фрактальді өлшемдерімен сипатталған. Бөлшектерді
агрегациялау жолымен қалыптасқан ұсақмасштабты кластерлер көрінетін жіптің
ауданы немесе диск тәрізді пішінді болып келеді, олар үшін D ≤ 3.
Өлшемдері 1 мм және одан көбірек болатын қатты бөлшектердің (құм,
графит) массалық күштері молекулааралық күштерден біршама көп болғандықтан,
фрактальді кластерлерді қалыптастыра алмайды. Алайда, оларға ұсақ
бөлшектердің агрегациялану жолымен қалыптасқан фрактальді кластерлер
орнығуы, яғни олар фрактальді тонмен орануы мүмкін.
Мандельброттың көлемді жиындары түріндегі мұндай объектілерді
үлкенмасштабты фрактальді құрылымдар деп атауға болады [45], 3 және 4
сурет.
Әр түрлі сұйықтардың арасындағы бөліну шекарасы тұтқыр саусақтар
деп аталатын фрактальді қисықты түзеді, мұндай қасиеттер көптеген
тәжірибелермен дәлелденген [48]. Газ фазасының болуы негізінде сұйықта
ұқсас фрактальді сурет байқалады. ((0,2(0,3 газ фазасының көлемді
концентрациясы кезінде ұсақмасштабты фрактальді құрылымдармен газсұйықты
ағынының көпіршікті режимі жүзеге асады. Газ мөлшерінің ұлғаюымен бірге
жеке көпіршіктер жинақталып, фрактальді құрылымға ие қаруды түзеді.
Қарулардың өлшемдері газсұйықты ағынның масштабтарымен салыстырмалы, олар
үлкенмасштабты фрактальді кластерлер болып табылады.

1 сурет. Бөлшектердің агрегациялық араласуларының екі есе шектелуі
нәтижесінде туындайтын кластер ( D = 1,71).

2 сурет. Сәулелендіретін электрондық микроскоптың көмегімен алынған алтын
кластер суреті.

3 сурет. Жасанды графит бөлшектерінің суреті.

4 сурет. Компьютер арқылы сызықты емес бейнелеу көмегімен алынған
Мандельброт жиыны.

Біз белгіленген кішігірім және үлкенмасштабты фрактальді
құрылымдардың физикалық қасиеттерінің өзара айырмашылықтарының болуымен
ерекшеленеді. Олардың ең негізгісі – кеңістіктік масштабқа тән қоспалар
концентрациясының өсуі, мысалы, кішігірім масштабты құрылымдарының максимал
өлшемі өседі, ал үлкенмасштабты құрылымдардікі кемиді.
Мультифракталдар – қазіргі заманға сай ғылымның күрделі объектілері.
Олар фрактальді өлшемдердің жинақталуы мен q-дің әр түрлі ретті өлшемінің
ықтималдылығымен сипатталады. Физикалық табиғатына сәйкес гетерогенді
ортаның турбулентті құрылымдарын мультифрактальдар деп қарастырған жөн.
Олардың өлшемдері мынадай формула арқылы анықталады:

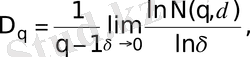
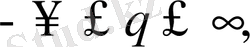(3)

мұндағы q – мультифрактальді сәтінің реті кез келген заттық санға тең болуы
мүмкін, 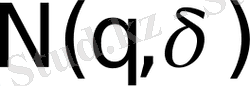– ықтималдылық әдіспен іске асатын ықтимал шамасы болатын
ұяшықтар саны, q = 0 болған кезде (3) формуладан ұяшықтардың көбінің
фрактальді өлшемдері Хаудсдорф бойынша жүреді: .
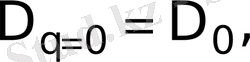
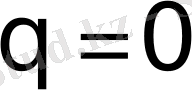Фрактальді объектілер өзіне тәндік және өзінді афиндік болып екіге
бөлінеді. Бірінші жағдайда ұқсастықтың коэфициенттері барлық бағыттарда
бірдей, ал екінші жағдайда – әр түрлі. Мультифракталдар үшін бұл
айырмашылық (3) формулада 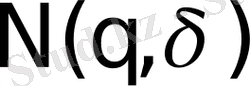есептелінумен сәйкес қосынды мен
ықтималдықтар сәттерінің шығаруы арқылы ескеріледі [49]

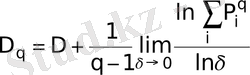(4)

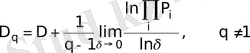(5)

Өзіне тән құрылымдар әр түрлі ықтималдылықтармен бірге өзара шығарылған
оқиғалар жиынтығына сәйкес олардың әр түрлі иерархиялық деңгейлерімен
орындалады.
Өзінді аффиндік – кез келген бағыттарда өлшемінің өзгеруі әр түрлі
кездейсоқ факторлардың бір уақытта болуының нәтижесінде тұрақсыздығымен
көрінеді, сондықтан ықтималдылық сәттерін шығаруымен сипатталады.
Ықтималдылықтардың мультипликативті орналасуының өзі араласудың пайда
болуының себебі болып табылатын – сипаттамаларының іс - әрекеті біресе
тығыз; біресе бос [50].
Фрактальді теория турбуленттіліктің әр түрлі біртексіздігінің
спецификасын өзінді афиндік мультифракталдардың спектральды теориясында
есептеуге мүмкіндік береді. Турбуленттіліктің мультифракталдар қасиеттерін
иеленетіндігін тәжірибелерден көруге болады. Қазіргі уақытта
мультифрактальді анализ қазіргі заманғы физиканың әр түрлі аймақтарында
кеңінен қолданылады. Біртекті және изотропты турбуленттілікте оның
құрылымды элементтері – құйындар өзіне тән мультифрактал болып табылады.
Олардың ұқсастық коэффициенті барлық кеңістіктік ауыспалылық жағынан
бірдей. Нақты шекті шарттармен анықталатын турбуленттілікте біртексіздік
пен анизатропияның болуы кезінде құрылымды элементтер өзінді афиндік
мультифракталдар түрінде қарастырылады – әр түрлі кеңістіктік және уақыттық
ауыспалылықтағы әр түрлі коэффициентті объектілер.
Келтірілген қысқаша шолудан әр түрлі құрылымдардың қалыптасуы
когерентті құйындар, бір және көп фазалы сұйықтықтың сорғыда ағатын
ағынындағы фракталды кластерлер мен мультифракталды объектілері түрінде
турбуленттілік құбылыстармен байланысты. Турбуленттілікті зерттеу ғылыми
негізде ғана емес, сонымен қатар тәжірибелік, әсіресе импульсті көбейту
кезінде гетерогенді сұйықта ағып өтетін нақты үрдістерді зерттеуде маңызы
аса зор болып табылады.

2. Турбуленттік сорғының кеңею қарқындылығының коэффициентін тәжірибе
арқылы анықтау

Сорғыда ағатын ағысты зерттеуге тәжірибелік және теориялық жұмыстардың
көптеген түрлері арналған [1-34]. Сорғыда ағатын ағымдарға білдірілетін
қызығушылық техниканың әр түрлі салаларына қажеттілігімен, маңыздылығымен
түсіндіріледі. Олардың тіптен бар екендігі, әрі олардың жұмыс үрдісінің
қарқындатуда (мысалы, турбулентті араласу үрдісін қарқындату үшін дүрсіл
үрдісіндегі ауа мен газ тәрізді отын ағымы) немесе оның үнемділігін
арттыруда шешуші рөл атқаратындығы рас.
Сонымен қатар, ағымдарды зерттеу турбуленттіліктің пайда болу
мәселелерін зерттеу аймағында жалпыфизикалық қызығушылық танытады.
Турбулентті ағыстың ең көп зерттелген түрі басымды ағым болып табылады [1].
Қоршаған ортаның бөлшектерінен және ағыстың өзінің тежелген бөлшектерінен
тұратын ағымның шекаралық қабатының қалыңдауы, бір жағынан көлденең
қимасының кеңеюіне, ал екінші жағынан, ағыстың потенциалдық ядросының
бірте – бірте қысқаруына әкеледі.
Турбулентті ағыстың кеңею қарқындылық коэфициентінің эмпирикалық мәні
[1] жұмысында анықталған кезде турбулентті ағыстың шекаралық қабатының
кеңеюі соңғы уақытқа дейін теориялық анализге берілмеді.
Қазіргі кезде турбулентті ағыстардың қасиеттерін [26] жұмысында
зерттеуде фракталдар теориясының қолданылуына байланысты сорғыда ағатын
ағымдардың шекарасына теориялық есептеулер жүргізуге мүмкіндік туды.
Ағыстағы турбуленттілік оның шекарасында пайда болатын когеренттік
құрылымдарды күйрету арқылы дамиды. Бұл құрылымдар [26] жұмыста
квазибөлшектер ретінде ұсынылған. Сонда турбулентті ағыстың шекарасының
кеңеюін квазибөлшектердің каскадты бөлінуімен түсіндіруге болады, мысалы,
олардың әрқайсысының екіге бөлінуі.
Скейлиндік каскадты үрдістер (тік каскад, инверсті каскад)
турбуленттілік дамыған ағыстың негізгі бөлігінде ағып өтеді және ықшамды
біртектілік пен изотропты қасиеттерге ие болады. Турбулентті ағыстың
негізгі бөліктерінде жылдамдықтардың өрістері Ферми – Дирак үлестіруі
көмегімен суреттелуі мүмкін, яғни Ферми – Дирак үлестіруінің тұжырымдалуы
кезінде комбинаторикалық пайымдалуларды қолдануға болады [14]. Сол кезде
бөлшектер санының орнына турбулентті және аутқымайтын сұйықтың берілген
жылдамдықтардың мәнінің жүзеге асырылу ықтималдылығы координаталарға
байланысты анықталады. Онда жүзеге асырылу ықтималдылығының мәні былай
өрнектеледі:

(6)

мұндағы - көлденең координата, φ, φ- турбулентті ағыстың кеңею
бұрышы. шамалары сақталу заңдарының шарттарына ұқсас мағынаны
білдіреді. j индексі есептің геометриясын анықтайды: - жазық ағыс,
– осьтік симметрия. (6) формулаға арқылы енген кеңею бұрышы
таза эмпирикалық тұрақтылық деп саналады. Ағыс шекарасының
фрактализациясының элементар модельдеріне сүйене отырып, [126] жұмыста осы
шаманың теориялық бағасын бере алды.

Ізделінген С0 мәні жазық және симметриялы осьті ағыстың негізгі
бөлігіне ғана қатысты жатады. Осы ұйғарымдар негізінде [26] жұмыстағы
ағыстың шекарасының фрактализациясын ескере отырып, С0 мәнін бағалауға
арналған мынадай формула алынды:

= (7)

мұндағы xi~ki, ~, ~, ki – сұйықтың бөлшегінің
квазиимпульсі, xi, ∆yi, ∆xi квазиимпульстарға сәйкес келетін сұйықтың
бөлшектерінің орын ауыстыруы. мәні – яғни, квазибөлшектердің
ұсақталынуы молекулярлы тұтқырлықпен шектеледі. [7] формуладан, каскадты
үрдістер әрекетіне ұжымдық және кеңістіктік эффектілер әсерін ескермей,
сонымен бірге турбулентті араласудың максималдылық және изотроптық
ұстанымдарын қабылдай отырып, қосылғыштардың шексіз санына дейін қосынды
жасауға болады. Осының нәтижесінде [26] жұмыста С0 = 0,226 алынды. Осындай
әдіспен, турбулентті ағыстың кеңею үрдісінің физикасы ауытқуларының
бұзылуы кезінде қоршаған ортаға импульстің берілуімен түсіндіріледі.

С0 = tgφ кеңею бұрышының тангенсін анықтау үшін [34, 35] жұмыстарында
келтірілген турбуленттіліктің әр түрлі деңгейіндегі турбулентті симметриялы
осьті ағыстың визуалды суреттері зерттелген болатын. Тәжірибелер диаметрі
d=8;16 мм симметриялы осьті каналдан ағып шығатын ауаның ағысымен
өткізілді. Ағыста турбуленттіліктің бастапқы құрылымын басқару жұқа
сақиналар түріндегі (қалыңдығы 0,70 мм, диаметрі d) жасанды
турбулизаторлармен, ось бойын ағыспен канал қимасына жақын орналастырылған,
сонымен қатар дыбыстық әсерімен бойлай (ағыс бойымен) айналу денелері
(өлшемдері L = 0.25÷0.5 d тән) орындалатын.

[34] тәжірибе нәтижелері ағыстың түрлі – түрлі бастапқы құрылымын,
яғни турбулентті соқтығысулардың түрлі қарқындылығын алуға мүмкіндік берді.
Қолданылған турбулентті ағыстың құрылымын басқару мүмкіндігі бізді
қызықтыратын изотропты және біртекті турбуленттіліктің n = 0,806 скейлинг
көрсеткішіне сәйкес келетін ағыстың сипаты біртекті және изотропты жағдайға
ұмтылу кезіндегі жылдамдықтың турбулентті соқтығысу қарқындылығының
асимптотикалық әрекеті туралы нақты анық қорытынды жасауға мүмкіндік берді.

Сонымен бірге ағынның (ұзындығы хd) [35] изотропизациясының
барлық жағдайларында →0,194 тенденциясы байқалады. Шектік өзіндік
ұйымдастырылған турбулентті ағыстың шамаларының табиғи флуктуациялары 19,4%
құрайды.

Келесі суреттерде турбулизацияның әр түрлі әдістері қолданылған
симметриялы осьті ағыстың көлеңкелі фотолары келтірілген. 5-суретте ағынның
суреттері Рдыб.=90 дб дыбыстық қысым деңгейдегі f=0÷1000 Гц жиілікті
акустикалық тербелістердің әсеріне сәйкес келеді. 6-суретте ағынның
суреттері дыбыстық тербелістер мен жасанды турбулизатордың өзара
әрекеттесуімен алынған. 7-суретте ось бойымен каналдың ішінде орнатылатын
денелердің айналуын қолданылатын ағыстың жасанды турбулизациясына сәйкес
келеді.

Турбулентті ағыстың шекараларының кеңею бұрышының тангенсін анықтау
үшін 1(в, г), 2(в, г) и 3(г) фотосуреттер алынған болатын. Өйткені, бұл
фотосуреттерде ε турбуленттіліктің бастапқы деңгейі үлкен мәндерге ие,
сондықтан ағынның жетілген турбулентті режимі канал қимасынан алыс емес
жерлерде басталады [34]. 7-суретте когерентті құрылымдардың күйреуі
кезіндегі батырылған ағыстың қоршаған ортамен турбулентті араласуының даму
кезеңдері айқын көрінеді. 7(г)-суретте турбуленттіліктің бастапқы деңгейіне
сәйкес ауытқымайтын қоршаған ортаға қарағанда турбулентті ағыстың негізгі
құрылымы жақсы көрінеді. 8-суретте С0 коэффициентін анықтаудың тәжірибелік
әдісін иллюстрациялау үшін визуалды суреттердің біреуінің (7г) сызбалық
бейнесі келтірілген. Бұл сызба батырылған симметриялы осьті турбуленттік
ағысты бейнелейді.

5 сурет. Турбулизаторсыз симметриялы осьті ауа ағысы.
u0=10мс. а – f = 0 Гц, б – f = 170 Гц,
в – f = 420 Гц, г – f = 1000 Гц

6 сурет. Турбулизаторы бар симметриялы осьті ауа ағысы
u0=10мс. а – f = 0 Гц, б – f = 170 Гц, в – f = 420 Гц, г – f = 1000 Гц

7 сурет. Сорғының орталық бөлігіндегі ағысы.
=: а – , б – в – , г – .
8 сурет. 7 (г) фотосуретінің сұлбасы.

Сызбадан ℓ және b мәндері анықталды. bℓ = С0 = tgφ қатынасы ағыстың
кеңею бұрышымен сәйкес келеді. Бұл қатынас С0 = 0,218 (0,22 үшін мән берді.
С0 анықтау әдісі бізбен [34, 35] жұмыстарда алынған басқа да нақты
фотосуреттерге де қолданылды. Берілген тәжірибеде С0 анықтау қателігі
фотосуреттер бойынша 3 – 5% құрайды.
Осы өлшеулерден алынған С0 орташа мәні С0 ( 0,22 тең, бұл [26]
жұмыстардың берілгендерімен байланысты. Тәжірибелердің кең бөліміндегі
мәліметтерімен теориялық есептеулердің мұндай сәйкес келуінің жақындығы
импульсін азайту арқылы квазибөлшектерінің каскадты күйреуінің моделін
көрсетеді және турбулентті ағыс шекарасында болатын негізгі физикалық
құбылыстарды нақты суреттейді.

3. Газдың жалынындағы және ауаның құйындық ағыстарындағы кластерлердің
әрекеттесуін зерттеу

Газды жалынның және ауаның турбулентті ағысының сезімтал құрылымының
тәжірибелік зерттеуі [35] ауыспалы аймақта ағысты симметрия түрде орап
алатын үлкенмасштабты тороидальді құйындардың қалыптасқанын көрсетеді.
Ағыстың теплерлік суреттерінің [34] анализі каскадты ұсақталудың
нәтижесінде күйреу арқылы төменгі ағыс бойында біртекті және изотропты
турбуленттіліктің ұяшықты құрылымы пайда болатын құйынды құрылымдардың
күрделі физикалық табиғатын анықтады. Құйынды кластерлер өзіне тән
дискретті де, толқынды да қасиеттерге ие [26]. Физикалық көзқарас бойынша
олар фракталдардың (мультифракталдардың), солитондардың, квазибөлшектердің
және т.б. қасиеттеріне ие деп айтуға болады.
[34] тәжірибелер нәтижелері бойынша практикалық жоспарда ағындағы
турбулентті және импульсті араласу үрдістерінің қарқындылығына қызығушылық
танытуда (9-сурет), газды шырақ жалынының және ауа ағыстарының құйынды
кластерлерінің сыртқы әрекетіне сезімталдығы анықталды (10-сурет). Бұл
өнеркәсіпті өндірістің жанармайлы құрылғыларындағы газ тәрізді отындарды
пайдалану кезінде өте маңызды. Турбулентті ағында газ тәрізді отынның жануы
басқа да әдістермен қатар өртенудің жоғарғы аумағының ұлғаюымен
қарқындатылады. Жалынның беттік аумағы құйынды кластерлердің газды
шырақтардың ағысындағы каскадты күйреуі мен пайда болу жиілігіне
пропорционалды түрде өзгеріп тұрады. Осы кезде өртенудің қарқындылығы
шырақтың өзіндегі жылу және масса алмасуының артуымен жүреді. Осындай
жанармайлы жану үрдісінің мынадай аэродинамикалық ұйымдасуы жану ядросы
мен өртену аумағында жанудың күшеюіне ықпалын тигізетін шырақтың түбіндегі
периферийлі қабаттарындағы қалыпты турбуленттіліктің жоғарғы дәрежесі
қамтамасыз етілген кезде жетеді. Турбуленттіліктің деңгейі өз кезегінде
генерирленген құйындардың негізгі бөлігіндегі каскадты бөлінуі мен
қарқындатылған ағыстың бастапқы және ауыспалы аймағындағы кеңістіктік
конфигурацияға және жиілікке байланысты. Алайда, ағыстағы үлкенмасштабты
құйынды кластерлердің қалыптасуымен газ тәрізді отынның жану үрдістері
қарқындылығының өзара байланысы қазіргі уақытқа дейін жеткілікті
зерттелмеген.
Жоғарыда айтылған фактілер бойынша газды факел жалынында генерирленген
құйынды кластерлердің тәжірибелік зерттеу нәтижелері мен есептеулерінің
теориялық нәтижелері алғаш рет осы жұмыста келтірілген.
Турбулентті ауа ағысы мен шырақтың құйынды құрылымдарының зерттелінуіне
өткізілген тәжірибе нәтижелері [34] жұмыста автормен толық сипатталған.
Газды жалынды бірнеше ретті визуалды бақылаудың кейбір нәтижелері 11-сурет
және 12-суретте келтірілген.

9сурет. Ағыс шеті мен осіндегі
құйындардың қалыптасуын өлшеу.

Ағыс осі: ○ – стабилизаторсыз, v – стабилизатормен;
● – стабилизаторсыз
ағыс шеті.

10 сурет. Re = 9600 кезіндегі жылдамдық пішіні. ○ – стабилизаторсыз,
v – стабилизатормен.

а

б
11 сурет. Газдың жалыны: а – ламинарлы жалын,
б – турбулентті жалын

11-суретте пропанды ауа қоспасының ламинарлы және турбулентті жалынының
мезетте алынған суреттері. Ауаның арту коэффициенті =1,02. Ағыс
қоспасы үшін Рейнольдс саны Re=6·103. Екі жағдайда да ағу шарттары бірдей.

12 сурет. Турбулентті жалындағы құйынды кластер.

Жалынның жасанды турбулизациясы (б кадры) дыбыстық қысымы Р = 90дб
деңгейіндегі өлшемсіз Sh = 0,4÷0,6 жиілігімен сәйкес келетін резонанс
жиілігінің бойланған (ағыс бойымен) акустикалық импульсімен шығарылды.
Ламинарлы жалынға қарағанда турбулентті жалынның фронты құйынды
кластерлермен өте қатты қиылуы нәтижесінде жану фронтының беткі жағы
көрінерліктей үлкеюіне әкелетіндігін суреттен көруге болады.
Ламинарлы және турбулентті жалынның температуралық өрістерін өлшеу
кезінде алынған жалынның орташаланған сипаттамалары [36], жалынның жасанды
турбулизация кезіндегі жылулық кернеуінің өсуін көрсетті (10-сурет).
Алдымызда белгіленгендей, турбулентті жану кезінде жалын фронты қисаяды
және шайылып кетеді, осы кезде оның беткі жағының артуы бақыланатын
жалынның таралу жылдамдығын да арттырады. Сонымен қатар, турбулентті жану
кезінде жанған жерінің ұзаруы артады, бірақ жалынның конус пішінді бейнесі
сақталады.
13-суретте айналған газды жалынның бұрынғы параметрлерінің режимі
кезіндегі көлеңкелі суреті келтірілген. Тәжірибе барысында алынған
визуалды суреттердің барлығында каналдан ағыстың ағуы мен қоспаның режимді
параметрлерінің бірдей шарттарын қадағалау нәтижесінде жалындағы құйынды
кластердің ұқсас кеңістіктік конфигурациясы тұрақты бақыланатынын белгілеу
қажет. Суретте турбулентті жалынның ауыспалы аймағында қалыптасқан құйынды
кластер айналып жүруінің бірдей бағытына ие екендігі көрініп тұр. Одан
кейінгі турбулизация турбуленттіліктің максимальді дәрежесі =19,4%
болып, біртекті және изотропты турбуленттіліктің өзіне тән құрылымдары мен
скейлинг көрсеткіші n=0,806 [35] басталу дәрежесіне дейінгі ағынның төменгі
бойындағы құйынды кластердің каскадты бөлшектелуімен қатар жүреді. Суретте
келтірілген құйынды қалыптасулар өзіне тән болатындықтан, құйынды
кластердің кеңістіктік масштабын зерттеу үшін олардың кез келгенін алуға
болады. Сондықтан құйынның сызықты өлшемдерінің нақты өлшеулерін алу үшін
оның бірінші рет бөлшектенуіне дейінгі ең ірі кластерін таңдап алуға
болады.
Құйынды кластерлердің белгілі бір геометриялық масштабына өлшеу өткізу
үшін [34] тәжірибеде алынған бізбен зерттелген визуалды суреттердің нақты
компьютерлік сызбасы құрылған. Компьютерлік сызбаның бірі (14-суретке
сәйкес) иллюстрация үшін 15-суретте көрсетілген, мұндағы x және r құйынды
кластердің өлшенетін сызықты өлшемдері. Тәжірибеде компьютерлік сызба
бойынша визуалды суреттерге сәйкес x және r өлшеніп, олардың хr қатынасы
анықталған болатын. Алынған сандық нәтижелерінің қатынасы 1,81 хr 1,98
мәндерінің интервалында өзгереді.

13 сурет. Әр түрлі жиілікті акустикалық импульсінің ықпалы кезіндегі
турбулентті жалынның температурасының профилі. Струхаль саны Sh:
● – Sh=0; ○ - Sh=0,45; ∆ - Sh=1,46; D=16мм; u0 =10 мcек.

14-сурет. Құйынды кластердің компьютерлік сызбасы (36 суреттен)

Әсер етуші құйындардың динамикасын зерттеуге аналитикалық ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.