Кванттық механиканың заңдары

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:

МАЗМҰНЫ

І. Кіріспе____________________________ ___________________________2
1. Қатты дене_______________________________ ____________________3
1.1 Қатты денелердің қасиеті____________________________ __________3
1.2 Кристалдану. Кристалдық денелер____________________________ __4

ІІ. Негізгі бөлім:
2.1 Сыртқы фотоэффект құбылысы және оның заңдары______________5-8
2.2 Фотоэффект теориясы. Эйнштейн теңдеуі______________________9-11
2.3 Фотонның массасы мен импульсі___________________________ _12-13
2.4 Жарық қысымы ___________________________________ _______13-16
2.5 Фазалық кеңістік___________________________ _______________17-18
2.6 Бозе-Эйнштейн және Ферми-Дирактың кванттық статистикалары_18-20
2.7 Металдағы азғындалған электрондық газдар___________________20-22
2.8 Жылу сыйымдылығының кванттық теориясы. Фонондар________22-24
2.9 Металдың асқын өткізгіштігі_______________________ ___________25
2.10 Қатты денелердің зоналар теориясы_________________________26 -28
2.11 Жартылай өткізгіштердің меншікті өткізгіштігі_______________29-32
2.12 Жартылай өткізгіштердің қоспалы өткізгіштігі________________33-36
2.13 Металдардың түйісуі____________________________ _________37-38
2.14 Екі жартылай өткізгіштің түйісуі___________________________3 9-41
2.15 Жартылай өткізгіштердің қолданылуы_______________________42 -43

ІІІ. Қорытынды__________________________ ______________________44

IV. Пайдаланған әдебиеттер_________________________ ____________45

І. Кіріспе:

Физика – материя қозғалысының жалпы және қарапайым формаларын,
қасиеттерін зерттейтін ғылым. Табиғаттағы әрбәр нәсре материя, олайболса,
олкеңістік пен уақыт бойынша үнемі қозғалыста болады. Сөйтіп, материя
қозғалысының механикалық, молекулалық, электромагниттік, атомдық және
ядролық формалары бар.
Физика – табиғаттың алуан – түрлі құбылыстары мен тәжірибелерге
негізделген ғылым. Табиғат құбылыстары физикалық шамалар арқылы
сипатталады. Физикалық шамалармен тәжірибе жасау негізінде физикалық заңдар
ашылады.
Қазіргі уақытта денелердің бір-бірімен өзара әсерлесуінің табиғатта
төрт түрлі күші бар. Олар: гравитациялық, электромагниттік, ядролық және
әлсіз өзара әсер күштері. Осы күштердің бәрі баықалатын жағдайларды біз
Әлемнің шексіз кеңістігінен, Жердегі кез келген денелерден, атомдар мен
атомдық ядролардан, элементар бөлшектердің барлық түрленулерінен
кездестіреміз.
Физика қазіргі табиғат танудағы озат ғылымдардың бірі болып табылады.
Ол ғылымның, техниканың, өндірістің әр түрлі салаларына зор ықпалын тигізіп
отыр.
Күрделі өндірістерді автоматтандыру үшін оған епті автоматтық
желілер, өндіріс роботтары, басқарушы микрокомпьютерлер және әр түрлі
электрондық бақылау - өлшеу аппараттары керек. Осындай жетістіктер
техниканың ғылыми негіздері радиоэлектроникамен, қатты дене физикасымен,
тағы да қазіргі физиканың бірқатар бөлімдерімен тығыз байланысты.

1. Қатты дене.

Бізді қоршаған дүниеде денелер көбінесе қатты, сұйық немесе газ
тәрізді күйлерде кездеседі.Қатты дене сұйыққа, сонан кейін газға айналуы
мүмкін.Ал сұйықтың газға, газдық сұйыққа айналуы мүмкін емес.
Үш күйдің әрбірінде денелердің өзара әрекетінің ерекшеліктері бар.
Қатты күйдегі денелер басқа денелермен өзара әрекеттескенде, өздерінің
көлемін және пішіндерін өте аз өзгертеді. Егер екі қатты дене жанасып,
тыныштықта тұрса, онда бір денеге сыртқы күш әрекет еткенде, ол бұл
әрекетті басқа денеге сыртқы күштің бағытыбойымен жеткізеді дәне деформация
туғызады. Күштің тудырған деформациясы жанасу ауданына тәуелді.

1.1 Қатты денелердің қасиеттері.

Сұйық және газдан қатты дененің ерекшілігі – оған күшті сыртқы күштер
әрекет еткенде, дененің көлемі және пішіні өте аз өзгереді. Бұл қасиет
қатты дененің атом және молекулалары берік байланысып, олардың өзара
арақашықтығының тұрақты болуымен түсіндіріледі. Қатты күйдегі денелер
кристалдық және аморфты денелерге бөлінеді.

1.2 Кристалдану. Кристалдық денелер.

Егер мұзды суық жерден жылы бөлмеге алып келсек, онда біраз уақыт
өткеннен кейін ол еріп кетеді. Басқаша айтқанда, қатты күйден сұйық күйге
айналады. Бұлай болатын себебі: бөлмедегі жылы ауаның энергиясы мұзға
беріледі, сөйтіп, мұз алдымен жылиды да, бірте-бірте ериді. Ал бөлме
температурасында қорғасынды ерітуге болмайды. Еріту үшін оны жоғарғы
температураға дейін қыздыру керек. Денені қыздыру оның сызықтық және
көлемдік өлшемдерінің ұлғаюына әкеліп соқтырады. Қатты денені қыздырғанда,
оның температурасы жоғарылап, ішкі энергиясы артады. Сөйтіп, тор
түйіндеріндегі бөлшектердің жылулық тербелістерінің энергиясы, яғни
тербеліс амплитудасы өседі. Бөлшектер энергиясының өсетіндігісоншалық, ол –
бөлшекті тор түйіндерінде ұстап тұрған күштерді жеңіп шығады. Сөйтіп, қатты
дененің кеңістік торы бұзылады. Демек, қатты дене сұйыққа айнала бастайды.
Заттың қатты күйден сұйық күйге айналу процесін балқу деп атайды.
Балқу процесі әр зат үшін белгілі бір тұрақты температурада ғана
орындалады. Осы тұрақты температураны сол заттың балқу нүктесідеп атайды.
Әр түрлі дененің балқу нүктесі әр түрлі.
Қатты денені балқытуға кеткен энергияның өлшемі меншікті балқу жылуы
деп аталады:

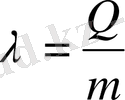
Балқуға кері процесті, яғни сұйықтың қатты денеге айналуын
кристалдану деп атайды.
Кристалл атомдары немесе молекулалары – кеңістікте орын алып, олардың
өзара орналасуы кеңістікте периодты түрде қайталанатын денелер.

ІІ. Негізгі бөлім:

2.1 Сыртқы фотоэффект құбылысы және оның заңдары

Электромагниттік толқындарды тапқан неміс ғалымы Генрих Герц 1887 ж.
электр ұшқындары пайда болатын вибратор саңылауына ультракүлгін
сәулелерімен жарық түсірілгенде электр ұшқындары көбейіп, электр зарядының
күшейетіндігін бірінші рет байқаған. Онан кейін ғалымдар осы құбылысты
зерттей отырып, мысалы теріс зарядтталған таза мырыш пластинаға
ультракүлгін сәулелері түсірілгенде онвң теріс заряды бірте-бірте кеміп,
керісінше оң зарядталатындығын анықтады (1-сурет). Осы екі құбылысты заттың
бетіне түсірілген жарық әсерінен заттан электрондардың бөлініп
шығатындығымен түсіндіруге болады. Олай болса, түскен жарық ықпалынан
заттан электрондардың бөлініп шығу құбылысын фотоэлектрлік эффект
(фотоэффект) деп атаймыз.

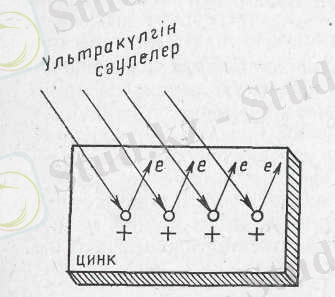
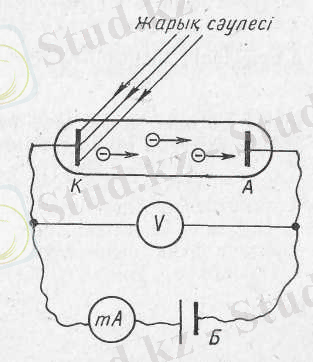
1-сурет
2-сурет
Фотоэффект құбылысын 1888 ж. орыс физигі А. Г. Столетов (1839-1896)
тереңірек зерттеді. Мұндай құбылыстар сыртқы фотоэлектрлік құбылыстар деп
аталады. Сыртқы фотоэффект құбылысын толығырақ түсіндіру үшін Столетов
мынадай тәжірибе жасады (2-сурет). Анод (А)
және катод (К) электродтары бар ішінен ауасы сорылған шыны түтік ток
көзімен қосылған. Монохромат жарық сәулелерінің әсерінен катодтан
электрондар бөлініп шығады, осындай электрондар фотоэлектрондар, ал олардың
ағыны фотоэлектр тогы немесе фототок деп аталады. Тізбектегі фототок
гальванометрмен (mA), Б-батарея қоздырған электродтар арасындағы
потенциалдар айырымы вольтметрмен V өлшенеді. Шыны түтіктегі катодты толқын
ұзындықтары әр түрлі жарық сәулелерімен сәулелендірудің нәтижесінде
Столетов мынадай заңдылықтарды қорытындылады:
1) жарық әсерінен катодтан тек теріс зарядты электрондар бөлініп
шығатындығы анықталады;
2) катодқа күлгін және ультракүлгін сәуелер түсірілсе бұл құбылыстың
күшейе түсетіндігі байқалады;
3) катодтан бөлініп шығатын электрондардың мөлшері катод бетінің
жарықталынуына немесе түскен жарық ағынына тура пропорционал болады.
Катод бетінен жарықтың әсерінен тек теріс зарядты электрондар бөлініп
шығатындығын 1899 ж. неміс ғалымы Ф. Ленард (1862-1947) және У. Томсон
электр және магнит өрістерінде зарядтардың ауытқуы кезінде олардың меншікті
зарядын анықтау арқылы дәлелдеді. Кейінірек осы қорытындыны 1922 ж. совет
физиктері А. Ф. Иоффе және Н. И. Добронравов зарядталған металл
тозаңдарының фотоэлектрлік құбылысын зерттеу арқылы дұрыс екендігін айтты.
Енді фотоэффект құбылысының вольт-амперлік сипаттамасын зерттейік. Яғни,
фототок күшінің (Iф) потенциалдар айырымына (U) тәуелділігін қарастырайық
(3-сурет).

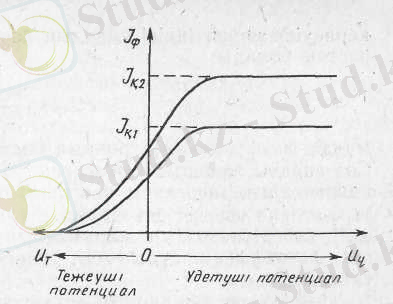
3-сурет
Жарық сәулесінің әсерінен катод бетінен ұшып шыққан электрондардың
белгілі бір кинетикалық энергиясы болады. Катодқа әсер етуші жарықтың
спектрлік құрамы және оның ағынының қуаты тұрақты болса, фототок күші
потенциалдар айырымына тәуелді болады, яғни

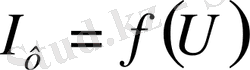
Үдетуші потенциалдар айырымы (Ur) артқанда фототокта (Iф) артады. Ал
үдетуші потенциалдың мәні белгілі бір шамаға жеткенде фототок күші өзінің
қанығу мәніне жетеді (Iқ). Өйткені катодтан шыққан электрондар түгелімен
анодқа жетеді. Сонымен қанығу фототок шамасы фотоэлектрондар санына
пропорционал болады:
Iк1=en, (1)
мұндағы n-катодтан бірлік уақыт ішінде шыққан электрондар саны, e-электрон
заряды.
Бұл тәжірибеден, катод пен анод арасындағы аотенциалда айырымы U=0
болғанда да, фототок шамасы нөлге тең болмайды, себебі электрондардың
бастапқы ν жылдамдықтарының әсерінен нөлге тең емес кинетикалық энергиясы
болады. Сөйтіп фотоэлектрондар электр өрісінің әсерінсіз-ақ осы энергияның
арқасында анодқа жете алады. Ал фототок нөлге тең болу үшін катод және анод
аралығында тежеуші потенциалдар айырымы UТ туғызуымыз керек. Сонда осы
кездегі фотоэлектрондардың оның тежеуші керннуіне көбейтіндісі олардың
бастапқы кинетикалық энергиясына тең болады:
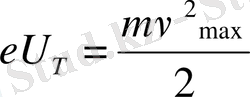, (2)
мұндағы νmax-электронның бастапқы максимал жылдамдығы. Сол сияқты жоғарыда
айтылған тәжірибеден, фотоэлектрондардың кинетикалық энергиясы мен оның
бастапқы максимал жылдамдығы катодқа әсер етуші жарық сәулелерінің тербеліс
жилігіне тәуелді, себебі катодтың жарықталуына байланысты. Бұдан фотоэффект
құбылысы үшін Столетов мынадай үш заңын тағайындайды.
1. Фотоэлектрондардың алғашқы максимал жылдамдығы фотокатодқа түскен
жарықтың интенсивтігіне тәуелді болмай, тек жарықтыі тербеліс жилігіне
байланысты анықталады.
2. Бірлік уақыт ішінде катодтан бөлініп шыққан фотоэлектрондар саны
түскен жарық интенсивтігіне пропорционал болады (өйткені қанығу тогы жарық
ағыны қуатына пропорционал).
3. Кез келген заттң әлі де болса фотоэффект құбылысын қоздыра алатын
жарық жилігін (ν0) фотоэффектінің қызыл шегі деп атайды.
Сонымен фотоэлектрондардың кинетикалық энергиясы жарықтың тербелістер
жилігіне тәуелді болады, өйткені катодқа түскен жарықтың тербеліс жилігі
көп болса, электрондардың жылдамдығы да соғұрлым көп болады.
Фотоэлектрлік құбылыстың сыртқы фотоэффектіден басқа да түрлері бар,
енді соларды қарастырайық.
Ішкі фотоэффект мазмұнын былайша түсіндіруге болады. Кристалдарға
немесе жартылай өткізгіштерге жарық сәулелері түскенде жарық жұтылады да
олардың құрамындағы кейбір электрондар сыртқа ұшып шықпағанымен, босанып
(зоналар теориясын еске алыңыз) толы зоналардан өткізгіштік зоналарға
ауысып қозғалады. Осының нәтижесінде жартылай өткізгіштің электрлік
кедергісі кемиді де, электр өткізгіштігі артады. Олай болса, жарық әсерінен
кедергісі кемитін жартылай өткізгіштер фотокедергілер деп аталады.
Вентильдік фотоэффектіде сыртқы фотоэффект сияқты жарықтың әсерінен
заттың бетінен фотоэлектрондар бөлінеді, бірақ олар сыртқа ұшып шықпай, тек
тежеуші қабат деп аталатын өте жұқа қабаттан бір беткей ғана өтеді де, сол
қабаттың үстіне орнатылған металл пластинаны зарядтайды, сөйтіп
фотоэлектрондар тежеуіш қабаттан кері қарай өте алмайды. Ал жарық түскенде
жартылай өткізгіш пен металл пластина аралығында электр өрісі болмайды.
Мұндай фотоэффектінің негізгі бір қасиеті күн сәулесі энергиясын тікелей
электр энергиясына түрлендіруге мүмкіндік береді.

2.2 Фотоэффект теориясы. Эйнштейн теңдеуі.

Фотоэффект құбылысын Максвеллдің электродинамика заңдарының негізінде
түсіндірмек болған пікірлердің бәрі нәтижесіз болды. Электр өрісінде
фотоэлектрондардың энергиясы өріс кернеулігіне, ал өріс кернеулігі болса
жарық интенсивтігіне тәуелді болады.
Олайц болса, жарық интенсивтігі артқанда электрондардың кинетикалық
энергиясы артуға тиіс, бірақ фотоэлектрондардың кинетикалық энергиясы жарық
интенсивтігіне байланысты болмай, жарықтың тербеліс жилігіне тәуелді
болады. Сонымен қатар электрондар металдан бөлініп шыққанда белгілі бір
жұмыс істеледі. Осы жұмыстың шамасын шығу жұмысы (А) деп атайды. Сөйтіп
фотоэлектрондар металдан бөлініп шығу үшін жарық толқыны өрісінен
электрондарға берілетін энергия мөлшері әлгі шығу жұмысына тең боларлықтай
болуы керек. Жарық жилігі фотоэффектің қызыл шегіне сәйкес жиліктен, яғни,
кем болмаса, жарық интенсивтігі қаншама аз болғанымен фотоэффект құбылысы
байқалады. Сонда жарық интенсивтігі кемігенде тек бөлініп шыққан
фотоэлектрондар саны ғана азайып, энергиясы өзгермейді.
Сонымен классикалық физика фотоэффект құбылысын түсіндіре алмады. Бұл
құбылысты атақты неміс физигі А. Эйнштейін 1905 ж. Планктың жарықтың үздік-
үздік сәулесінің энергия шығаруы жөніндегі идеясын пайдаланып, бірінші рет
жарықтың кванттық теориясы негізінде түсіндірді. Эйнштейіннің пікірінше
белгілі бір жиліктегі жарық кеңістікте тарала отырып жеке проциялар түрінде
зат бетінде жұтылады және шығарылады. Олай болса, жарық тарағанда энергия
кванттары ағын түрінде таралады. Яғни жарық энергиясының кванттары фотондар
деп аталады. Сонымен жарық ағыны дегеніміз фотондар ағыны болып есептеледі.
Сөйтіп жарық квантының энергиясы Планктың идеясымен сәйкес келіп, ол
жарықтың тербеліс жилігіне пропорционал болады.
Эйнштейннің пікірінше фотоэффект құбылысы кезінде әрбір электрон жеке
әрбір фотонның әсерінен бөлініп шығады. Яғни, әрбір фотоэлектрон тек бір
фотон энергиясын жұта алады. Сөйтіп жұтылған фотон энергиясы (һν)
фотоэлектронды металл бетінен бөлініп шығатын шығу жұмысына (Аш) және оның
кинетикалық энергиясына айналады. Олай болса, Эйнштейн теңдеуі мына түрде
жазылады
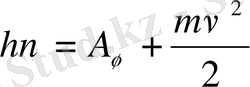, (3)
Бұл теңдеу фотоэффектіге қатысты негізгі мәселелерді түсіндіруге
мүмкіндік береді. Эйнштейнше жарықтың интенсивтігі жарық сәулелерінің
кванттар (проциялар) санына пропорционал және металдан бөлініп шыққан
фотоэлектрондардың санын анықтайды. Фотоэлектрондардың жылдамдығы Эйнштейн
теңдеуі бойынша тек жарық жилігіне және металдың тегі мен оның бетінің
күйіне тәуелді шығу жұмысы арқылы анықталады. Ол жарықтың интенсивтігіне
байланысты.
Егер жарықтың жилігі ν белгілі бір минимал ν0 мәнінен артық болса,
онда кез келген зат үшін фотоэффект байқалады. Фотоэлектронды металдан,
оған кинетикалық энергия берместен бұрын шығарып алу үшін, Аш шығу жұмысы
істелуі керек. Олай болса, жарық энергиясы бұл жұмыстан артық болуы тиіс

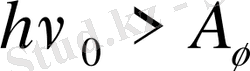
Сөйтіп шектік жиілік ν0-фотоэффектінің қызыл шекарасы деп аталады. Оны мына
өрнек арқылы жазамыз:
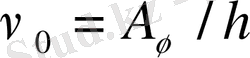, (4)
Шығу жұмысы Аш заттың тегіне тәуелді. Сондықтан әр түрлі заттар үшін
фотоэффектінің шектік жилігі (ν0) түрліше болады. Мысалы, 4-суреттегі шыны
түтік ішінде орналасқан катод (К) және анод (А) электродтары әр түрлі
материалдан жасалғандықтан олардың фотоэффект шектік жиліктері әр түрлі
болады. Оны тежеуші кернеуі (UT) мен фотоэлектрондар жилігінің арасындағы
тәуелділік арқылы көрсетуге болады (4-сурет). Мұндағы ν0 (К) және ν0 (А)
катод және анод

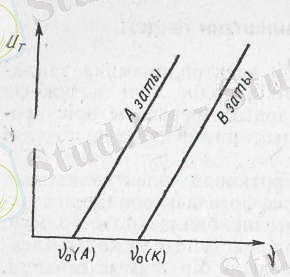
4-сурет
материалдарының фотоэффект қызыл шектік жиліктері. Ал тежеуші кернеуі мен
жилік арасындағы байланысты 2, 3 және 4 өрнектерден мынадай түрде жазуға
болады, яғни
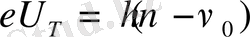, (5)
Эйнштейн теңдеуінен Планк тұрақтысын анықтауға болады. Ол үшін жарық
толқынының жилігін (ν), шығу жұмысын (Аш) тәжірибе жүзінде анықтап және
фотоэлектрондардың кинетикалық энергиясын өлшеу керек. Сөйтіп, Планк
тұрақтысының жылулық сәуле шығару және фотоэффект әдістерімен өлшеп алынған
мәндерінің бір-бірімен дәлме-дәл келуі заттардың жарықты шығаруы мен
жұтуының үздікті сипаты жөніндегі болжамдардың дұрыстығын дәлелдейді.
Әрине, Эйнштейн теңдеуінің дұрыстығын әр түрлі эксперименттар арқылы
тексерген. Солардың ішінде өте ерекше мұқият вакуумды сфералық конденсатор
әдісін қолданып жасаған – совет физигі П. И. Лукирский (1894-1954) мен С.
С. Прилежаев болды.
Егер жарық интенсивтігі өте жоғары болса (мысалы, лазерлік сәулелер
шоғы), онда көпфотонды (сызықсыз) фотоэффек қозады. Яғни, металдан бөлініп
шыққан фотоэлектрон ббір ғана фотон энергиясы емес, N санды фотондар (N=2,
3, 4, 5, ...) энергиясын алады. Ал көпфотонды фотоэффект құбылысын мынадай
теңдеу арқылы өрнектеледі:
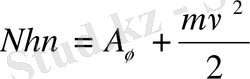, (6)
Көпфотонды фотоэффект қызыл шегінің жилігі мынадай:
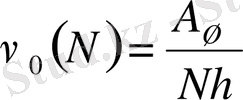, (6,а)

2.3 Фотонның массасы мен импульсі

Жарық шығару және жұтылу кезіндегі энергия һν-ге тең бөлшектер ағыны
болып есептеледі делік. Олай болса, сәуле шығару және жұтылу кезінде
байқалатын жарықтың қасиеттері корпускулалық (бөлшек) деп аталады. Жарық
бөлшегінің өзі фотон немес жарық кванты болып есептеледі.
Сөйтіп, фотоэлектр құбылысынан жарықтың корпускулалық қасиеттері бар
екендігі байқалады. Бөлшектер сияқты, фотонныңі да белгілі энергиясының
Е=һν порциясы бар. Салыстырмалылық теориясына сәйкес энергия барлық уақытта
массамен мына қатыс арқылы Е=mc2 байланысты. Фотонның энергиясы
болғандықтан, оның массасы мына түрде анықталады:
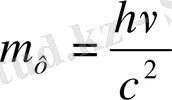, (7)
Фотонның тыныштық күйдегі массасы m0 болмайды, яғни ол тыныштықта өмір
сүрмейді. Олай болса, (7) өрнектегі анықталатын масса фотонның қозғалыс
кезіндегі массасы, фотонның белгілі массасы мен жылдамдығы бойынша оның
импульсін табуға болады
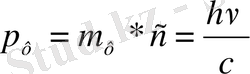, (8)
Фотонның импульсі жарық сәулесімен бағыттас болады. Фотонның заряды
және магнит моменті болмайды. Неғұрлым жилігі көп болса, соғұрлым фотонның
энергиясы мен импульсі көп болады да,жарықтың корпускулалық қасиетітері
соғұрлым айқынырақ байқалады. Планк тұрақтысы аз шама
болғандықтан,көрінетін жарық фотондарының энергиясы да аз болады. Мұның
дәлелі ретінде совет физигі С. И. Вавиловтың тамаша тәжірибелерінде ең
нәзік құрал, адамның көзі бірлік кванттармен өлшенетін жарықталынудың
түрліше екендігін сезе алатындығы анықталды.
Сөйтіп, ғалымдар жарықты бөлшектар ағыны деп түсіндірді. Әрине, бұл
Ньютонның корпускулалық теориясына қайта оралу сияқты болып көрінеді. Бірақ
интерференция, дифракция құбылыстарында жарықтың толқындық қасиеттері
білінсе, фотоэлектрлік құбылыста оның корпускулалық қасиеттері білінеді.
Сөйтіп жарықтың әрі корпускулалық қасиеттері болатындығынбайқадық. Сонда
жарықтың табиғаты екі жақтылы – дуализмдік қасиеттері болады. Жарықтың
таралуы кезінде оның толқындық қасиеттері, ал заттармен әрекеттескенде
корпускулалық қасиеттері Байқалады. Әрине осының бәрін көзбен көріп байқау
мүмкін емес, бірақ шындық. Бұл тек микродүниедегі процестерде болатын
ғажайып құбылыстар. Бертін келе екі жақтылық қасиет тек жарыққа ғана тән
емес, ол электрондарда да, басқа элементар бөлшектерде де ашылды. Мысалы,
электронның корпускулалық қасиеттерімен бірге толқындық қасиеттері де бар.
Сол сияқты электрондардың дифракциясы байқалады.
Сонымен микрообъектілердің мұндай ерекше қасиеттері микробөлшектер
қозғалысының қазіргі теориясы – кванттық механиканың жәрдемімен
түсіндірілді.

2.4 Жарық қысымы.

Максвелл ұсынған жарықтың электромагниттік теориясы басқа әсерлермен
қатар жарыққа қарсы кездесетін тосқауылдарға қысым түсіретіндігін болжап
айтқан. Электромагниттік теория бойынша жарық денегіміз электромагниттік
толқындардыі бір түрі болғандықтан жарық түскен дененің бетінде электр тогы
пайда болады, себебі жарық толқындары өрісі әсерінен дене құрамындағы
электрондар өріс бағыты бойынша қозғалады. Ал ток бағыты болса, жарықтың
таралу бағытына перпендикуляр болады (5-сурет). Бұл тоққа жарық толқынының
магнит өрісі әсер етеді. Ол күштің бағыты жарықтың таралу бағытына сәйкес
келіп, жарық түскен бетке перпендикуляр болады да, жарық дененің бетіне
қысым түсіреді.

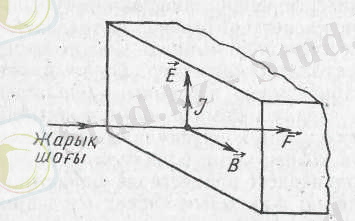
5-сурет
Жарықтың кванттық теориясының пайда болуы жарық қысымының себебін өте
оңай түсіндіруге мүмкіндік береді. Фотондардың импульсі болатынын өткен
тақырыпта айттық, олай болса олар өздерін жұтатын денеге өз импульсін
береді. Бірақ импульстің сақталу заңына сәйкес дененің импульсі жұтылған
фотондар импульсіне тең. Сондықтан тыныштықтағы дене қозғалысқа келеді.
Сөйтіп дененің импульсінің өзгеруі Ньютонның екінші заңына сәйкес, денеге
күш әсер ететінін білдіреді. Олай болса, жарықтың қысым түсіретін себебі
фотонның импульсі бар екендігін дәлелдейді. Енді осы тұрғыдан жарық
қысымының шамасын есептеп шығарайық.
Егер де бірлік уақыт ішінде дене бетінің бірлік ауданына перпендикуляр
бағытта N фотон түскен болса, онда шағылу коэффициенті r дене бетінен rN
фотон шағылып кері серпіледі. Ал фотонның жұтылған бөлігі (1- r)* N болады.
Сөйтіп әрбір жұтылған фотоннан денеге p=hνc мөлшерде импульс ауысады да,
барлық жұтылған фотондардан оған (1- r)* N hνc мөлшерде импульс беріледі.
Дене бетінен кері шағылып серпілген фотонның импульс мөлшері 2p=2hνc
болады. Сөйтіп дененің бетіне түскен барлық фотоннан денеге бірлік уақыт
ішінде мынадай мөлшерде импульс ауысады:

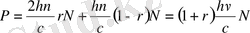
мұндағы Nhν=Eж –дене бетінің жарықталынуы, яғни бірлік уақыт ішінде дене
бетіне перпендикуляр бағытта түсетін жарық энергиясының ағыны. Егер
Eжс=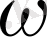шамасын жарық энергиясының көлемдік тығыздығы десек, онда кез
келген дененің бетіне перпендикуляр бағытта әсер ететін жарық қысымы
мынаған тең болады:
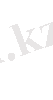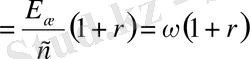Рқ, (9)
Кванттық теорияның негізінде қорытылып шығарылған (9) формула
Максвеллдің электромагниттік теориясындағы шамамен сәйкес келіп тұр.
Сонымен жарық қысымын әрі кванттық теорияның, әрі толқындық теорияның
негізінде өте жақсы түсіндіруге болады.
Енді жарық қысымын қалайша өлшеуге болады осыған тоқталайық.
Жарық қысымы өте аз шама. Мысалы, ашық күндері бір шаршы метрге
небәрі 4*10-6 Н күш ғана әсер етеді. Жарық қысымын алғаш рет орыс физигі П.
Н. Лебедев 1900 ж. өлшеді.
Лебедевтің приборы, жіңішке шыны қылдың шетіне жеңіл қанатшалар (а,б)
жапсырылған өте жеңіл стерженьнен тұрады (6-сурет).

Приборауасы сорылып алынған ыдыстың ішіне тұтас орналастырылған. Жарық
стерженьнің бір жағына орналасқан қанатшаларға түсіріледі. Қысымның шамасы
l жіптің иірілу бұрышы арқылы байқауға болады.

6-сурет
Әрине ыдыс ішіндегі ауаны мүлдем сорып алу мүмкін емес. Сондықтан
қанатшалар мен ыдыс ішіндегі қалған молекулалардың қозғалысы да жіпті
ширатады. Сонымен қатар, қанатшаларының беттерінің әр түрлі қызуы да жіптің
ширатылуына әсер етеді. Сол кездегі эксперименттік техника дәрежесінің
төмендігіне қарамастан, өте үлкен ыдыс және өте жұқа қанатшалар алып,
Лебедев осы қиыншылықтардың бәрін жеңе білді. Ең соңында жарықтың қатты
денелерге қысым түсіретіні дәлелденіп, өлшенді. Ол Максвеллдің болжамымен
дәл келді. Онан кейінірек, Лебедев өте нәзік тәжірибе жасап, жарықтың
газдарға түсіретін қысымын өлшеді.
Жарық қысымы кейбір ғарыштық құбылыстарда байқалады. Мысалы,
кометалар құйрығының пайда болуы және оның күн сәулесі таралу бағыты
бойынша созылып орналасуы жарықтың комета құйрығын түзетін зат бөлшектері
мен газ молекулаларына механикалық күштер әсерінен болады.

2.5 Фазалық кеңістік.

Егер классикалық статистикада ұқсас бөлшектердің бір тобының екінші
тобынан ажыратылатындығы айтылса, кванттық статистикада, керісінше, ұқсас
бөлшектердің ажыратылмаушылық принципін түсіндірдік. Оның үстіне спиндік
сандарының бүтін және жартылай болу себептерінен бөлшектер әр түрлі
статистикалық заңдылықтарға бағынатын болады.
Айталық, берілген жүйе n бөлшектерден түзілсін. Сонда жүйедегі
бөлшектердің барлық импульстері мен көпөлшемді кеңістік берілсін.
Кеңістіктің әрбір нүктесінде 6n саны сәйкес келеді, себебі әрбір бөлшектің
күйін 3 координатамен (x, y, z) және осы координаттарға сәйкес импульстің 3
проекциясын (px, py, pz) анықтайды. Сонымен, осы кеңістіктегі өзара
перпендикуляр координаттық осьтер саны 6n-ге тең. Сондықтан осындай 6n
өлшемді кеңістік фазалық кеңістік деп аталады. Сөйтіп, жүйедегі әрбір
микробөлшектің күйін осы 6n өлшемді фазалық кеңістік анықтайды, өйткені осы
бөлшекке сәйкес жүйедегі барлық бөлшектердің координаттары мен импульстері
осындай болады.
Енді 6n өлшемді фазалық кеңістікті кішігірім элементар ұяшықтарға
бөлейік, сонда барлық бөлшектердің координаттарының жинағы – q, ал олардың
импульстерінің проекцияларының жинағы – р болсын.
Сонымен зат бөлшектерінің корпускулалық және толқындық қасиеті және
Гейзенбергтің анықталмаушылық қатыстары осы элементар ұяшықтардың көлемі
Планк тұрақтысы һ3-тен кем болмайтынын көрсетеді. Әдетте, осы элементар
ұяшықтарды фазалық көлем деп атайды.
Егер де жүйедегі бөлшектің координаттары мен импульстерін ескермей,
тек қана квантталған энергиясы белгілі болса, онда жүйенің күйін үздіксіз
емес, дискретті функцияның үлестірілуі арқылы сипаттауға болады.
Осындай функцияның үлестірілуі туралы өте маңызды өрнектің жалпы түрін
американ физигі Д. Гиббс (1839-1903) тапты. Бұл тұжырым Гиббстің канондық
үлестірілуі деп атайды.
Кванттық статистикадағы Гиббстың канондық үлестірілуінің түрі мынадай
f (En)=Ae-En(kT, (10)
мұндағы А-тұрақты шама, n-барлық кванттық сандардың жиыны, ол жүйенің күйін
сипаттайды.
Сонда белгілі бір жүйенің ықтималдық тығыздығы деп, функцияның
үлестірілуін айтуға болады. Олай болса, жүйенің ықтималдық тығыздығы
мынаған тең
dW=f(q, p) dqdp, (11)
Сөйтіп dW жүйе күйінің координаттары мен импульстерінің q, q+ dq және р, р+
dp аралықтарында болатын ықтималдығын көрсетеді.

2.6 Бозе-Эйнштейн және Ферми-дирактың кванттық статистикалары

Біз бұдан бұрын классикалық статистикада қарастырылған идеал кванттық
статистика тұрғысынан зерттейік. Онда идеал газ молекулалары мен атомдардан
түзіледі делік. Олай болса, кванттық жүйеде ұқсас бөлшектердің жиынтығы осы
күйді сипаттайтын толтыру саны (N) деп аталатын сандардан түзіледі. Осы
сандар кванттық күйдің толтыру көрсеткішін сипаттайды. Егер бөлшектер
жүйесі спиндік саны нөлге немесе бүтін сандарға тең болатын бозон
бөлшектерінен түзілсе, онда толтыру сандары кез келген бүтін сандарды
қабылдайды, яғни (0, 1, 2, 3, ..)
Ал бөлшектер жүйесі спиндік саны жартылай сандарға тең болатын фермион
бөлшектерінен түзілсе, онда толтыру сандары тек екі мәнді қабылдайды, яғни
бос күйлер үшін 0 мәнді де, толтырылған күйлер үшін 1 мәнді болады.
Сонымен барлық толтыру сандары жүйедегі бөлшектер санына тең болу
керек. Сөйтіп, берілген кванттық күйдегі бөлшектердің орташа санын кванттық
статистика көмегімен есептеуге болады.
Ендеше идеал газдағы бозон бөлшектерінің орташа санын Бозе-Эйнштейннің
кванттық статистикасы бойынша есептеуге болады. Д. Бозе (1858-1937) – үнді
физигі. Сонда бозондардың энергиясы бойынша үлестірілуі Гиббстың канондық
үлестірілуіне негізделген. Яғни, Бозе-Эйнштейннің кванттық статистикасы
бойынша бөлшектердің орташа толтырылу саны мына өрнек бойынша есептеледі
, (12)
мұндағы NБ –энергиясы Еп кванттық күйдегі бозондардың орташа саны, Т-
термодинамикалық температура, k – Больцман тұрақтысы, ЕБ – энергияның
нормалау тұрақтысы.
Фермиондардан түзілген идеал фермигаздар Ферми-Дирактың кванттық
статистикасымен сипатталады. Олай болса, Ферми-Дирактың (Э. Ферми 1901-1954
ж. өмір сүрген итальян физигі) кванттық статистикасы бойынша бөлшектердің
орташа толтыру саны мына формула бойынша есептеледі.
, (13)
мұндағы NҒ - энергиясы Еп кванттық күйдегі фермиондардың орташа саны, ЕҒ –
нормалану тұрақтысы немесе Ферми энергиясы деп аталады.
Егер 1 болса, онда Бозе-Эйнштейн мен Ферми-Дирактың
үлестірулері классикалық Максвелл-Больцман үлестірілуіне ауысады, яғни
, (14)
мұндағы
А=е (ЕБ, ЕҒ)(кТ), (15)
Сөйтіп өте жоғары температураларда Фермигаз бен Бозегаз классикалық
идеал газ тәрізді болып өзгереді.
Кванттық статистикада азғындалған бөлшектер жүйесі деп аталатын
бөлшектер болады. Олардың қасиеттері классикалық статистикада заңдарына
бағынатын жүйенің қасиеттерінен өзгеше болады. Мысалы, біз қарастырып
отырған Фермигаз бен Бозегаз азғындалған газдар болып есептеледі. Сонда
газдардың азғындауы әсіресе өте төменгі температураларда және үлкен
қысымдарда айқын біліне бастайды.
(14) және (15) өрнектердегі А шамасы азғындау параметрі деп аталады.
Осы А1 болғанда, Ферми-Дирак және Бозе-Эйнштейн үлестірулері Максвелл-
Больцман үлестірілуіне ауысады.
Белгілі бір Та температурасының төменгі мәндерінде идеал газдардың кванттық
қаситтері айқын біліне бастайды, яғни ұқсас бөлшектердің қасиетіндей күйге
келеді. Олай болса, осындай температура (Та) азғындау температурасы деп
аталады.

2.7 Металдағы азғындалған электрондық газдар

Кванттық теорияға сәйкес кристалл электрондарының энергиясы атомдағы
сияқты квантталады, яғни үздіксіз мәндерді қабылдай алады. Паули принципі
бойынша ең төменгі деңгейде атомның тек электроны ғана орналаса алады., ал
қалғандары қос-қостан жоғары деңгейлерді толтырады. Атомдар жақындай түскен
сайын күшейе түсетін өзара әсер пайда болады.
Енді металдағы электрондардың өткізгіштік зоналардың деңгейлері
бойынша таралуын қарастырайық. Тіпті металл температурасы Т=0 К болғанның
өзінде төменгі деңгейлердің әрқайсысында екі электрон болады, ал қалған
деңгейлер бос қалады (8-сурет). Бұл суретте ордината осінің бойына берілген
деңгейдегі электрондардың орташа саны, ал абсцисса осінің бойына энергияның
мәндері салынған. Сөйтіп, металдағы электрондардың өткізгіштігін Ферми-
Дирак үлестірілуіне бағынатын идеал

7-сурет
газ деп қарастыруға болады. Олай болса, бұл үлестірілу мына түрде
көрсетіледі
, (16)
мұндағы Еп –берілген деңгейдің энергиясы, Еғ – Ферми деңгейі деп аталатын
жүйенің параметрі. Осы (16) өрнек берілген Еп деңгейдің электрондармен
толу ықтималдығын көрсетеді. Сонымен 7-суреттегі тұтас қисық сызықтың Т=0 К
болғандағы функциялық графигімен дәл келетіндігін байқаймыз.
Шынын да, егер Еп Еғ болса, онда NЕҒ=1. Ал Еп Еғ болса , онда
NЕҒ=о. Сөйтіп, Т=0 К кезіндегі Еғ Ферми деңгейіэлектрондар толған жоғары
деңгеймен дәл келеді. Егер Еп=Еғ болса, кез келген температура кезінде (16)
өрнектің 1мен2-ге тең мәні болады. Демек, Ферми деңгейі электронмен толығу
ықтималдығы жартыға тең энергетикалық деңгеймен дәл келеді.
Металдар үшін жасалған тәжірибелердің нәтижелері Еғ –тің
температураға аса тәуелді емес екендігін көрсетеді, демек, онша жоғары емес
температурада, яғни kTЕп=Еғ Ферми деңгейінің мәнінің абсолют нөл кезіндегі
мәнінен айырмашылығы аздау. Ал Т0 К болғанда Ферми-Дирактың үлестірілуі 7-
суреттегі көрсетілген пунктир қисық сызық түрінде болады. Осы қисықтың
ординатасы деңгейдің орташа уақыт бойынша электронмен толғандығын
сипаттайды. Алайда Т температурасы кезіндегі электрон үлестірілуінің 0 К
кезіндегі үлестірілуінен елерліктей айырмашылығы шамамен kT ретті аймақта
ғана байқалады. Демек, жылулық қозғалыс барлық электрондардың тек аз ғана
бөлігіне әсер етеді. Сондықтан электрондардың орташа энергиясының
температураға тәуелділігі әлсіз болады.
Енді өткен тарауда айтылған Та азғындау температурасын қалай табуға
болады, соған тоқталайық. Біз жоғарыда көрсетілген kTЕғ қатынасы кезінде
металдағы электрондық газ өте азғындалған күйге келеді. Олай болса,
электрондық газдың осындай күйі мына теңдік арқылы сипатталады kTа=Еғ.
Осындай азғындау температурасын Та табуға болады. Және де осы теңдік
кванттық эффектің одан әрі болмайтын шегін көрсетеді. Міне, осы кездегі
электрондардың азғындау температурасы Т0=104 К болады. Ал осы кездегі
азғындалғанэлектрондар саны металдағы барлық электрондар санының 10-5
үлесіндей ғана болады.

2.8 Жылу сыйымдылығының кванттық теориясы. Фонондар

Квантық теория бойынша еркін электрондар қозғалысында толқындық сипат
болады. Электрондық толқындар кристалдық торда болатын ақауларда шашырайды.
Ал толқын шашырауы кристалл ішіндегі электрондардың ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.