Ықтималдылықтар теориясының элементтері

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 43 бет
Таңдаулыға:

Кіріспе

Қазіргі кездегі ғылым мен техниканың қарыштап өсу дәуірінде ықтималдықтар теориясының әдістері практиканың сан алуан салаларында кеңінен қолданып физика, химия, биология құбылыстарының, техника мен экономика процестерінің заңдылықтарын жан-жақты және терең түсінуге орасан зор ықпалын тигізуде.

Орта мектептердегі жаңа бағдарламаларға сәйкес алгебра пәніне ықтималдықтар теориясын енгізу және оның оқыту әдістемесін жасау алға қойылған міндеттердің бірі. Ықтималдықтар теориясы туралы алғашқы зерттеу жұмыстары ХҮІІ ғасырда басталды. Европа елдерінде әр түрлі құмар ойындардың кең таралуына байланысты әр ойыншы өзінің жеңілмеу ықтималдығын алдын ала анықтауға тырысты. Сол кездегі математиктер де бұл мәселеге назар аударып бірнеше рет қайталанатын кездейсоқ оқиғалар туралы заңдылықтар алуға талпынды.

ХҮІІІ ғасыр аяғы мен ХІХ ғасыр басында А. Муавр, Л. Эйлер, Н. Бернулли, француз П. Лаплас, С. Пуссон, неміс ғалымы К. Гаусс геодезия мен астрономия өркендеуіне қатысты өлшеу қателіктерін бағалау, ату теориясындағы снарядтардың жағдайларын анықтау үшін ықтималдықтар теориясының ролін көрсету мақсатында ғылыми жұмыстар жүргізді.

ХІХ ғасыр ортасында Ф. Гальтон, Л. Больцман, А. Кетле, А. М. Ляпунов, П. Л. Чебышев, А. К. Колмагоров сияқты ғалымдар жиындар теориясы, нақты айнымалылар функциялар теориясы, функционалдық анализ сияқты жоғары математиканың жаңа табыстарына сүйенетін ықтималдықтар теориясының өркендеуіне негіз салды.

Ықтималдықтар теориясының дамуына байланысты оның адамзат өмірінде қолдану мүмкіндігі артты. Жалпы алғанда ықтималдықтар теориясының әдісі ғылымның барлық саласына өз үлесін қосады. Ал математика ғылымында алатын орны ерекше.

ХХ ғасырдың екінші жартысынан бастап құбылыстардың сандық өлшемдері әр түрлі процестердің, атап айтсақ, өндірісті математикалық модельдеу мен ғылыми шығармашылықтың алғашқы шарты болды, яғни ықтималдық ерекше маңызға ие болды. «Оқиға туралы ғылым» көптеген мамандық иелерінің: инженерлер, экономистер, дәрігерлер және басқа да саладағы мамандардың ортасына енді. Бүкіл әлемде осы ғылымға қызығушылықтың артқаны соншалық, тіпті ықтималдықтар теориясы жиі қолданатын болды деп айтсақ, қателеспейміз.

Қазіргі таңда ықтималдықтар теорисының әдістері кең қолданыс табатын ғылым мен техниканың жаңа салаларының пайда болуы және олардың тез қарқынмен дамуына байланысты математиканың бұл тарауына деген сұраныс күрт артып отыр. Атап айтқанда, кейінгі кезде ықтималдық теориясын медицинада және биология, әскери ғылым мен косманавтика, лингвистика, психология теориясы мен оқыту теориясы, т. б ғылымда да қолдана бастады. Бұлар - ақпарат теориясы, сенімділік теориясы, сапаны статистикалық бақылау, тәжірибені жоспарлау және т. с. с. сондықтан да ықтималдық теориясы мен математикалық статистика аэлементтері тек қана жоғары немесе арнаулы оқу орындарында ғана емес, жалпы білім беретін орта мектептерде оқытылуда.

Ықтималдықтар теориясы мен математикалық комбинаторика, статистика элементтерін мектеп тәжірибесіне енгізу қазіргі қоғам талабына сай математикалық білім берудің мақсатынан, яғни оқушыларды әдіснамалық тұрғыда тәрбиелеуде, математика курсының дүниетанымдық көзқарасына бағдарлауына, терең әрі негізделген пәнаралық байланыстарды құрудың мүмкіндіктерінен шығады. Бұл оқу материалдары адамның ақпаратты, сауатты түсінуіне және талдауға білікті болуына, нақты тәуелділіктердің ықтималдық сипатын және оның түрлі формасын анықтауына, қарапайым есептеулерді жүргізе алуына өте қажет.

Қазақстан Республикасының орта білім беру мемлекеттік стандартында математикада ықтималдық теориясы мен математикалық статистика элементтері бойынша оқушыларға қойылатын талаптар ауқымы айқындалған.

Комбинаторика, ықтималдық теориясы мен математикалық статистика элементтері бастамалары математикалық білім беру бағдарламасының мазмұнынан нақты орын алады.

Комбинаториканың кейбір элементтері б. з. д. ІІ ғасырдың өзінде-ақ Үндістандабелгілі болған.

ХІІ ғ. Бхаскара бірігу мен орын ауыстырулардың кейбір түрлерін есептеді. Үнді ғалымдары бірігулерерді поэтикада, шығармашылық туындылар мен өлең құрылымы туралы ғылыммен байланыстыра игерген деп болжайды, мысалы, п буыннан тұратын ұзақ және қысқа буынды бірігулердің мүмкін мәндерімен байланыстырады.

Апиан (ХҮІ ғ. ), Штифель мен Тартальяға тәуелсіз француз математигі Эригон (ХҮІІ ғ. ) өзінің «Практикалық арифметикасында» (1634) 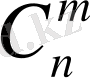- і анықтайды. Екінші француз авторы А. Такке «Арифметика теориясы мен практикасы» (1656) кітабында бірігулер мен ауыстыруларға бір тарауды толығымен арнайды.

«Комбинаторика» термині 1666 ж. Г. Лейбництің бірігулер мен ауыстырулар ілімі ғылыми негіз болып табылатын «Комбинаторика өнері туралы толғам » атты еңбегінен кейін қолдана бастады. «Орналастырулар» ұғымын алғаш рет Я. Бернулли өзінің 1713 ж. жарық көрген атақты «ARS conjectandi»(«Болжау өнері») кітабының екінші бөлімінде қарастырды. Ол біз қолданып жүрген «ауыстырулар» терминін енгізді. Ал «бірігулер» терминін Б. Паскаль да қолданған.

Жоғарыда айтылғандар диплом тақырыбын осылай таңдауға себеп болды.

Диплом жұмысының мазмұнына ықтималдықтар теориясы және жаратылыстану ғылымдары бағытындағы комбинаторика элементтеріне қолданып шығарылатын көптеген негізгі мысалдар қарастырылды.

Диплом жұмысының мақсаты комбинаторика және ықтималдықтар теориясы сапалы білім беру оқу үрдісін ұтымды ұйымдастыруғы қолданыс мүмкіндіктерін қарастыру.

Алға қойған мақсатқа жету үшін төмендегі міндеттер шешімін тапты:

-оқу -әдебиет көздеріне шолу жасалып, талдаулар жүргізу;

-комбинаторикалық есептердің теориялық негіздерін қарастыру;

-тақырыптың ерекше қарастырылуының себебі, оқу әдістемелік құралдармен қамтамасыз етуді қарастыру;

-оқушыларға теориялық білімді меңгертуде ақпараттық технология мүмкіндіктерін пайдалана отырып жүргізу.

Дипломдық жұмыстың бірінші тарауында комбинаторика элементтері туралы айтылса, екінші тарауда ықтималдықтар теориясының білім беруде қолдану мүмкіндіктері кқрсетілген.

Математикалық комбинаторика ұғымы

Комбинаторика қандай да бір шектелген жиынның элементтерінен құрастырылған бірігулердің (біріктірулердің) әр түрлі тектерімен айналысады. «Комбинаторика» термині латынның combina - «біріктіру» деген сөзінен шыққан.

Кез келген А оқиғасының ықтималдығын классикалық анықтама бойынша есептеу үшін А-ға тиісті нүктелердің (А оқиғасына «қолайлы жағдайлардың») санын барлық нүктелер (барлық «жағдайлар») санына бөлуіміз керек. Бұл - комбинаторика ережелерін қолдану арқылы жеңіл жүргізіледі.

Комбинаторика - математика тарауларының бірі. Мұнда шекті жиын элементтерінің түрлі қосылыстары, басқа айтқанда, әр қилы конфигурациялары қарастырылып, олардың сандары саналады және де есептеледі.

Теориялық зерттеу тұрғысынан алғанда комбинаторика алғаш рет XVII ғасырдағы Я. Бернулли, Эйлер еңбектерінде қарастырылған. Ұлы математиктердің бұл шығармаларында комбинаторикалардың кездесуі бір жағынан алғанда тұрмыстық сан алуан мұқтаждарына байланысты болса, ал екінші жағынан алғанда, математиканың өз ішіндегі дамуларымен ұштасып жатыр.

Классикалық анықтамаға негізделген ықтималдықтарды 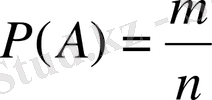есептеу А оқиғасының пайда болуына қолайлы, элементар оқиғалар саны m - ды және барлық элементар оқиғалар саны n - ды табу тіреледі. Ықтималдықтар теориясында m мен n мәндері, ілгеріде көрсетілгендей оп-оңай анықтала бермейді. Бұларды табу үшін қайсыбір жиын элементтерін түрліше алу тәсілдерін қарастыруға тура келеді. Мәселен, жәшіктегі әріптер жиыны a, b, c элементтерінен құралған десек, онда бұл жиыннан әріптерді: 1) бір-бірден 3 тәсілмен аламыз (a, b, c) ; 2) екі-екіден 6 тәсілмен аламыз (ab, ba, ac, ca, bc, cb) ; 3) үш-үштен 6 тәсілмен аламыз (abc, acb, bac, bca, cab) .

Мұндағы алынған әріп тіркестерінің бір-бірінен айырмашылығы элементтерінде, не элементтерінің орналасу ретінде болып отыр. Мұндай тіркестер - жиын элементтерінің комбинациясы (қосылысы) болып, бірнеше реттелген жиындар жасайды. Мысалы, көрсетілген үш элементті жиыннан әрқайсысы екі элементтен 6 реттелген жиын алып отырмыз. Сондай-ақ 4элементті {a, b, c, d} жиыннан әрбір екі элементтен тұратын 12 реттелген жиын алуға болады және және т. с. с. Сонымен, шешуі: «нешеу», «неше тәсілмен» деген сұрауларға жауап беруді қажет ететін есептер комбинаторикалық есептер делінеді. Мұндай есептерді шешумен айналысатын математика саласы комбинаторика деп аталады.

Кейінгі жылдары комбинаториканың практикада кең қолданыс табуына электрондық есептегіш техниканың дамуы шектеулі математика ролінің артуы негізгі себеп болып отыр.

Комбинаториканы пайдаланып, оқиға ықтималдығын анықтау таңдаманы жиыннан алу тәсіліне байланысты. Мұны түсіндіруді мысалдан бастайық.

1-мысал. Елімізде автомашиналардың серияларын анықтау ісімен мемлекеттік автоиспекция шұғылданады. Олар екі, үш әріптен неше комбинация жасайтынын білуі тиіс. Бұл фактіні байланыс қызметкері де, кодылау мамандары да білуге тиіс. Сонымен, орыс алфавитіндегі 32 әріптен үш әріптен құралатын комбинацияны неше тәсілмен жасауға болады.

Шешуі: бұл есепті шешу әріптер жиынынан алынатын үш әріп комбинациясына қойылатын талапқа байланысты. Түсінікті болу үшін бұл әріптердің әрбіреуін формасы бірдей жеке карточкаларға жазайық. Сөйтіп оларды топтастырайық, яғни бір колода етейік. Сонда колодадағы карточкалар жиын болады. Әріптерді колодадан екі түрлі жолмен таңдап алуға болады.

Бірінші тәсіл (қайталанбайтын таңдама) . Бірінші алынатын әріп колодадағы 32 әріптің бірі болады, яғни оны 32 тәсілмен алуға болады. Ал, екінші әріп колода да қалған 31 әріптен алынады. Сонда шығатын әр түрлі екі әріпті комбинациялар саны 32 ⋅ 31 = 992 болады. Бұл екі әріпті тіркестердің әрқайсысы үшінші алынатын әріппен тіркесіп үш әріпті тіркес құрайды. Сонда олар 32 ⋅ 31 ⋅ 30 = 29760 тәсілмен алынады. Бұл жағдайда әрбір үш әріпті тіркестегі әріптер әр түрлі болып кездеседі.

Екінші тәсіл (қайталанатын таңдама) . Бірінші алынған әріп таңбасы белгіленген соң, ол колодаға қайыра салынады. Сонда екінші алынатын әріп те колодадағы 32 әріптің бірі болады. Олай болса, екі әріпті тіркестіреді 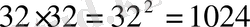тәсілмен алуға болады. Осы сияқты үш әріпті тіркестер

32∙32∙32= 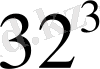=32768

тәсілмен жасалады. Бұл жағдайда үш әріпті тіркестердің жасалуына ешқандай шек қойылмайды, яғни мұнда әрбір әріп бір тіркестердің ішінде екі рет, үш рет қайталанып келуі мүмкін.

Сонымен, 32 әріптен үш-үштен алу таңдама болып табылады. Бірінші жолы колодадан қай әріп алынатыны белгіленгеннен кейін, колодаға ол қайта салынған жоқ. Сондықтан мұндай таңдама қайталанбайтын таңдама деп атаймыз. Екінші жолы колодадан алынған әріп белгіленіп алынғаннан кейін, ол қайтадан колодаға салынады. Сонда екінші әріп колодаға онда екінші әріп колодаға 32 әріптің ішінен алынады. Үшінші әріпті алғанда өзгермейді. Сондықтан бұлай таңдауды қайталанатын таңдама деп атайды. Ал, элементтері алынып отырған жиын, яғни 32 әріп жиыны бас жиын болады. Әдетте, бас жиындағы әріптер сол жиын элементтері болады.

Көбейту ережесі . Егер А жиыны a ₁ , a ₂ , …, a _m , элементтерінен, яғни m элементтен, ал В жиыны b ₁ , b ₂ , …, b _k элементтерінен, яғни k элементтен құралатын болса (бұл екі жиын бір жиыннан алынуы да мүмкін), онда олардың әрқайсысынан бір-бір элементтен ылынған әр түрлі (a _i , b _j ) комбинациялары саны mk болады (i = 1, 2, …, k) .

Шынында да, бұлардың (a _i , b _j ) түрінде m горизонталь және k вертикаль жолдардан тұратын мына таблицаға орналастыруға болады.

1 - кесте

b ₁

b ₂

…

b _k

ВА: a ₁

b1: (a ₁ , b ₁ )

b2: (a ₁ , b ₂ )

…: …

bk: (a ₁ , b _k )

ВА: a ₂

b1: (a ₂ , b ₁ )

b2: (a ₂ , b ₂ )

…: …

bk: (a ₂ , b _k )

ВА: …

b1: …

b2: …

…: …

bk: …

ВА: a _m

b1: (a _m , b ₁ )

b2: (a _m , b ₁ )

…: …

bk: (a _m , b _k )

Бұл кестедегі әрбір (a _i , b _j ) тек бір реттен ғана кездеседі. Олардың барлық саны - mk . Бұл ереже жиын саны екіден артық болғанда да орындалады. Мысалы, элементтер саны сәйкес m, k, h болатын үш жиын А = {a ₁ , a ₂ , …, a _m }, B = {b ₁ , b ₂ , …, b _k }, C = {c ₁ , c ₂ , …, c _h } берілсін. Әр жиыннан тек бір элементтен ғана алынған әр түрлі (a _i , b _j , c _l ) үш элемент комбинациясын жасауға болады, мұндағы i = 1, 2, …, k және i = 1, 2, …, h. Олардың саны m, k, h болады, өйткені А және В жиындарынан алынған әрбір (a _i , b _j ) пары үшінші жиынның әрбір элементімен комбинацияланады. Бұл комбинациялар саны, әрине (mk) h = mkh санына тең. Енді комбинаторика ұғымын ықтималдықтар теориясының есептерін шешуге қолданамыз. Ол үшін формулаларды қорытудың қажеттігі туады. Бұл формулалар екі түрлі жағдайда қарастырылады. Біріншісі қайталанбайтын таңдама үшін болса, екіншісі қайталанатын таңдама үшін болады.

Комбинаториканың негізгі элементтері

Табиғатта, қоғамда, ғылым мен техникада, өндіріс орындарында, күнделікті өмірде әртүрлі әдістермен шешілетін, шешімдері көп есептер жиі кездеседі. Мұндай есептерді шешумен айналысатын математика саласы комбинаторика деп аталады. Комбинаториканың қарапайым бөлімдері орналыстырулар, алмастырулар, терулер деп аталады.

Комбинаториканың негізгі принципі. Әр қайсысы шеткі А _1, A _2, …, A _k жиындары берілсін. осы жиындардың жазылу нөмерлеріне қарап, бұл міндетті түрде, бір - бірлеп 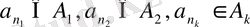элементтерін алалық. осындай тәртіппен алынған 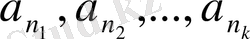элементтерін кортеж деп атайды және оны былай жазады.

Т е о р е м а. А _1, A _2, …, A _k жиындарының элементтерінен жасалған барлық кортеждердің саны n(A ₁ ) n(A ₂ ) …n(A _k ) көбейтіндісіне тең.

Д ә л е л д е у. Толық математикалық индукция әдісін қолданамыз. Индукцияны k бойынша жүргіземіз. k=2 болсын. A ₁ = 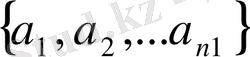және A ₂ = 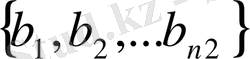деп белгілелік. a _n1 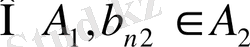элементтерінен (а _n1 , b _n2 ) кортежін құралық. Сонда кортеж парға айналды. Сөйтіп мұндай кортеждердің саны n(A ₁ ) ∙ n(A ₂ ) көбейтіндісіне тең. Сонымен, k =2 үшін теорема дәлелденді.

Мысалдар.

1. Бірде - бір цифры қайталанбайтын төрторынды сандардың саны қанша?

Шешуі. Төрторынды санды (i, j, k, l) кортежі деп қарастырамыз. i - дің орнында 1, 2, 3, 4, 5, 6, 7, 8, 9 цифрларының бірі тұра алады. j - дің орнында қалған 9 цифрлардың біреуі тұра алады, өйткені бұл жерде нөлде болуы мүмкін. Сондай - ақ k және i -дің орнында тұра алатын цифрлардың саны - 8 және 7. Сөйтіп, көбейтінді теоремасы бойынша әртүрлі және цифрлары қайталанбайтын төрторынды сандардың саны n= 9∙9∙8∙7=4536.

2. Телефон станциясы төрт цифрдан тұратын нөмері бар телефон аппараттарын қамтамасыз етеді. Станция жабдықтайтын барлық аппараттар саны қанша?

Шешуі. Әрбір аппараттарын нөмерін ( i, j, k, l) кортежі деп қарастыруға болады . i, j, k, l элементтері цифрлардың қайсысын болса да қабылдай алады. Демек, барлық телефон аппараттарының саны n =10∙10∙10∙10=1. Кейбір оқулықтарда «кортеж» дегеннің орнына «бір- бірлеп алынған комбинация» деп те атайды.

Қайталанбайтын таңдамалар үшін комбинаторика формулалары.

1 . О р н а л а с т ы р у л а р. Түрлі комбинаторикалардың ұғымын енгізудің бірнеше жолдары бар. Орналастырулар үшін де осылай айтуға болады.

Ықтималдықтарды есептеуге қолайлылығын пайдаланып, орналастырулар ұғымын кортеждер арқылы берелік.

n элементтен тұратын M={a ₁ , a ₂ , … a _n } жиынынан k көлемді кортеж құралық. Бұл жерде « k көлемді кортеж » деп отырғанымыз кортежге енетін элементтердің саны k -ға тең болатындығын көрсетеді. М жиыннан (a _i1, a _{i2, …,} a _ik ) кортежі екі түрлі әдіспен жасалуы мүмкін: екіншісі - кортежге M жиынының элементі бірнеше рет кіруі мүмкін. Бірінші жағдайда кортеждерді, n элементтен k - дан жасалған орналастырулар деп, екінші жағдайда кортеждерді n элементтен k - дан жасалған қайталамалы орналастырулар деп атайды.

Т е о р е м а: n элементтен k - дан жасалған орналастырулар саны n(n-1) (n-2) . . . (n-k+1) көбейтіндісіне, ал қайталамалы орналастырулар саны n ^k -не тең.

Д ә л е л д е у: Орналастыруларды былай жасап шығалық: алдымен М жиынынан a _i1 элементін аламыз; содан кейін қалған n - 1 элементтердің ішінен a _i2 элементін аламыз. Кортеж элементтерін тағы да сол сияқты біртіндеп ала отырып, ақырында, қалған n - (k - 1) элементтердің ішінен a _ik элементін аламыз. Сөйтіп, (a _i1, a _{i2, …,} a _ik ) кортежі шығады. Сонда, көбейтіндінің теоремасы бойынша, барлық кортеждердің саны n(n-1) . . . (n-k+1) көбейтіндісіне тең болады. Теореманың бірінші бөлігі дәлелденді. Енді, қайталамалы орналастыруларды жасап шығалық: алдымен М жиынынан a _i1 элементін аламыз да, оны тіркеп болғаннан кейін М жиынының өзіне қайта оралтамыз; содан кейн М жиынының тағы да a _i2 элементін аламыз және оны тіркелгеннен кейін қайтарамыз. Міне, осы процесті қайталай отырып, (a _i1, a _{i2, …,} a _ik ) кортежін жасап шығарамыз. Сонда, көбейтіндінің теоремасы бойынша мұндай кортеждердің саны n⋅n⋅…⋅n=n ^k -не тең болады. Теорема толық дәлелденді.

Демек, n элементтен k - дан жасалған орналастырулар саны n(n-1) (n-2) (n-k+1) көбейтіндісіне, ал қайталамалы орналастырулар саны n ^k - не тең, яғни n элементтен k - дан жасалған орналастырулардың жалпы саны үшін 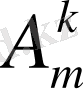, ал қайталамалы орналастырулар саны үшін 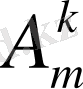белгілерін енгізсек:

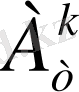= n(n-1) (n-2) . . . (n-k+1) = 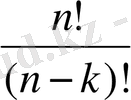(1. 1)

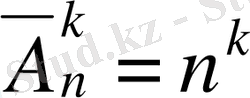(1. 2)

мұнда n! - эн факториал деп оқылады, ол 1-ден n - ге дейінігі натурал сандардың көбейтіндісіне тең, яғни n! =123… n , ал 0! =1 деп қабылданады.

1-мысал. 7 әріптен төрт- төрттен неше тәсілмен алуға болады. Шешуі: Есеп шарты бойынша n =7, k =4 енді (1. 1) формуланы пайдалансақ:

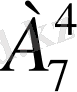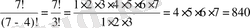
2-мысал. Үш ойын сүйегін лақтырғанда қанша жағдайлар болады. Шешуі: формула бойынша 6 ³ =216 - ға тең, өйткені n =6 және n=3. Себебі үш ойын сүйегін лақтырғанда пайда болатын ұпайларда ( i, j, k) кортежін жасалық, мұндағы i, j, k 1, 2, 3, 4, 5, 6 сандарының тек біреуін қабылдайды, сондықтан іздейтін сан формула бойынша ізделінеді. Екі ойын сүйегін лақтырғанда барлық жағдайлар саны 6 ² =6 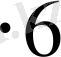=36. Егер S ойын сүйегін лақтырсақ, онда барлық жағдайлардың саны 6 ^s -не тең болар еді. Сол сияқты m теңгені лақтырғанда барлық жағдайлар саны 2 ^m -не тең.

3-мысал. 7 жолаушысы бар лифт 10 этаждың әрқайсысына тоқтап өтеді. Әрбір жолаушы қай этажда түсіп қалам десе бәрі-бір. Әрбір этажда бірден артық жолаушы түсіп қалмау ықтималдығы қандай?

Шешуі: Тәжірибедегі барлық жағдайлардың, яғни элементар оқиғалардың санын есептеу үшін 7 адамның қайсысы болсада біреуі i -ші этажда түсіп қалуын а арқылы белгілейік. Сонда бір жағдай деп отырғанымыз (a ₁ , a ₂ , … a _n ) кортежі болады. Ал бұл - қайталамалы орналастыру. (1. 2) формуланы қолданып барлық жағдайлардың санын табамыз: n = 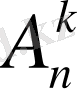= 10 ⁷ .

А арқылы «әр этажда бірден артық жолаушы түсіп қалмайды» оқиғасын белгілейік. А қолайлы кортеж (a ₁ , a ₂ , … a ₁₀ ) болады, бірақ ол орналастырудың өзі. Демек бірдей екі формуланы қолданып, қолайлы жағдайлар санын табамыз:

Енді А -ның ықтималдығын есептейміз:

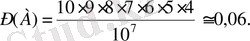
2. А л м а с т ы р у л а р. N элементтен N -нен алынған орналастыруларды алмастырулар деп атайды. N элементтен жасалған алмастырулар санын P _n арқылы белгілейді. Сонымен,

P _n = n!=1∙2∙3∙ … ∙n (1. 3)

Орта мектепке арналған оқу құралдарында алмастыруды шекті жиынның элементтерін реттеу әдісі есебінде анықтайды. Сонда екі әр түрлі алмастыру дегеніміз - жиынды реттеп шығудың екі түрлі әдісі. Кортеж арқылы анықтағанымызда алмастыру ұғымы осы мағынада қалып қоятындығын түсіну

қиын емес.

1-мысал. Жас бала кубиктерді қатар қойып ойнап отырған, ал кубиктерде А, А, М, Л әріптері жазылған. Сонда АЛМА сөзінің шығу ықтималдығы қандай?

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.