НЬЮТОН ЗАҢДАРЫНЫҢ ҚОЛДАНЫЛУЫНА МЫСАЛДАР

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 48 бет
Таңдаулыға:

М А З М Ұ Н Ы

КІРІСПЕ
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... .. 3
1 МЕХАНИКАДАҒЫ НЕГІЗГІ ҰҒЫМДАР
... ... ... ... ... ... ... ... ... ... ... ... ... 5
1.1 Кеңістік. Уақыт. Қозғалыс
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... 5
1.2 Санақ денесі. Санақ жүйесі. Жылдамдық. Үдеу
... ... ... ... ... ... ... ... ... ... ... . 16
1.3 Бір қалыпты айнымалы қозғалыс
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 19
2 Ньютонның заңдары
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
25
2.1 Ньютонның бірінші заңы
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... . 25
2.2 Ньютонның екінші заңы
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... .. 31
2.3 Ньютонның үшінші заңы
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... . 33
2.4 Бүкіл әлемдік тартылыс заңы. Бүкіл әлемдік
тартылыс тұрақтысы
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... . 34

2.5. Инерциялық масса және гравитациялық масса
... ... ... ... ... ... ... ... ... ... ... . 36

2.6. Қозғалыс мөлшерінің сақталу заңы
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 37
2.7. Серпімділік күштері
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... 39
2.8. Үйкеліс күштері
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... 40
3 НЬЮТОН ЗАҢДАРЫНЫҢ ҚОЛДАНЫЛУЫНА МЫСАЛДАР ... ... ... . 42
3.1 Эйнштейннiң салыстырмалылық принципi. Майкельсон тәжiрибесi ... ... .
42
3.2 Жылдамдықты қосудың релятивистiк заңы
... ... ... ... ... ... ... ... ... ... ... ... ... 47
3.3. Галилейдің түрлендірулері
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
. 49
3.4 Бүкіләлемдік тартылыс заңының қолданылуы
... ... ... ... ... ... ... ... ... ... ... ... 51
ҚОРЫТЫНДЫ
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... . 55
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
... ... ... ... ... ... ... ... ... ... ... ... ... ... 56

КІРІСПЕ

Жалпы физика курсын оқыту үрдісінде ең басты қиналатын мәселесі
теориялық материалды практика жүзінде пайдалана білу мен өтетін
құбылыстардың механизмін түсіну екендігі кімге де күмән туғызбайды. Бұл
теориялық материалдың физикалық мәніне түсінбей, оны механикалық түрде есте
сақтап қалуынан болады. Ал ондай білімнің күнделікті тұрмыста кездесетін
кейбір физикалық құбылыстардың мәнін түсіндіруге, физикалық есептерді
шығаруға ешбір көмегі тимейді. Физиканың логикалық есептерін шығару
математикалық есептерді шығаруға қарағанда қиынырақ, себебі мұнда үнемі
математикалық түрлендірулерді қолданып, есептің шешімін таба алмайсың. Бұл
есептер үшін басты шарт - құбылыстың физикалық мәнін түсіну, сол арқылы
логикалық теңдеу құру. Сонда ғана есептің ақиқат шешімін табуға болады.
Тақырыптың өзектілігі жоғарыда айтылған шарттарды ескере отырып
дипломдық жұмыста механикалық қозғалысты сипаттайтын негізгі ұғымдар мен
түсініктерге тереңірек тоқталып, динамика заңдарының басты моменттерін
көрсете отырып, осы қозғалыс заңдарының өмірде қолданылу формалары мен
техниканың дамуына әсері көрсетіледі.
Сондықтан бұл дипломдық жұмыс физиканы саналы түрде меңгеруге
талпынушыларға Механика бөлімі бойынша оның қандай тақырыпты жете
түсінетінін, нені үстірт білетінін анықтауға мүмкіндік жасайды.
Дипломдық жұмысты орындау барысында біз келесі мақсаттарды көздедік:
- қозғалыс ұғымының салыстырмалығын математикалық өрнектер көмегімен
өрнектеу, оларды оқып-білуде және олармен жұмыс кезіндегі қарапайымдылығын
талдау;
- механикалық әсер ету мен гравитация түсініктерін динамика заңдары
арқылы мәнін ашу;
- Ньютон құрастырған әлемнің механикалық көрінісін бейнелеу.
Көрсетілген мақсаттарға жету үшін келесі міндеттерді жүзеге асыруға
қажет :
- кеңістік, уақыт, жылдамдық, үдеу түсініктеріне анықтама беру;
- инерция, күш, гравитациялық масса, салмақ ұғымдарының мағынасын
ашу;
- тең әсерлі күштер, консервативті күштер, тепе-теңдік шарттары
жөнінде және динамика заңдарының күнделікті өмірде қолданылу
мысалдарын қарастыру.

1 МЕХАНИКАДАҒЫ НЕГІЗГІ ҰҒЫМДАР

1. Кеңістік. Уақыт. Қозғалыс.

Механика - физиканың денелер қозғалысын зерттейтін бөлімі. Механикада
қарастырылатын мәселе - дененің кез келген уақыт мезетіндегі орнын анықтау.
Денелердің қозғалысын қарастырғанда, көп жағдайда, олардың
деформациялануы ескерілмейді. Қозғалыс кезінде денені құрайтын бөлшектердің
ара қашықтықтары өзгермейтін болса, онда ондай денені абсолют қатты дене
дейді. Абсолют қатты денелер қозғалысын қарастырғанда, олардың өлшемдерін
көбінесе ескермейді. Берілген жағдайда (есепте) өлшемдерін ескермеуге
болатын денені материялық нүкте деп атайды [1].
Дене қозғалады дегенде, оның немен салыстырғанда қозғалатынын
айтпасақ, сөзіміз мағынасыз болады, өйткені механикалық қозғалыс әрқашан
салыстырмалы ұғым. Қозғалмайды деп алынған денені санақ денесі дейді. Санақ
денесі және ара қашықтық пен уақытты өлшеуге арналған құралдар санақ
жүйесін құрайды. Әдетте, санақ жүйесіне белгілі бір координаттар жүйесі
бекітіледі (1, а-сурет). Материялық А нүктенің орны санақ жүйесінде
координаттар арқылы немесе радиус-вектормен, яғни координаттар басынан
берілген А нүктесіне жүргізілген вектормен анықталады (1, б-сурет).
Дене қозғалғанда оның берілген санақ жүйесінде белгілі бір ретпен
басып өтетін нүктелер жиынын траектория дейді.
Қозғалыстағы материялық нүктенің кеңістіктегі орнын анықтау үшін х,у,z
үш координат (1, а-сурет), жазықтықтағы орнын анықтағанда х және у екі
координат (1, б-сурет), түзудің бойымен қозғалғанда бір координаттың
мәні қажет (1, в-сурет).

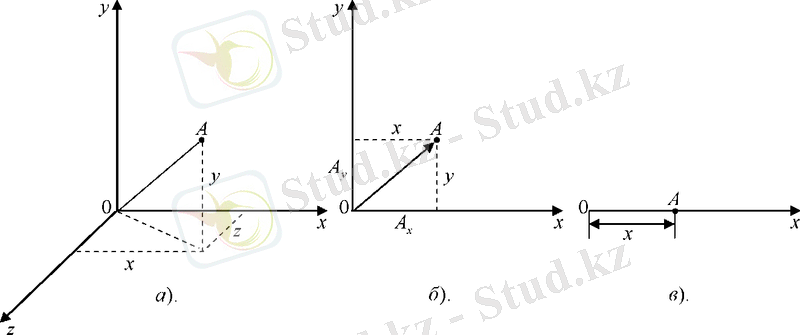
1-сурет.

Кеңістік ұғымы обьектілерді бақылау мен тәжірибелік пайдалану
негізінде қалыптасты.
Уақыт ұғымы адамның оқиғалардың ауысуын сезінуінің нәтижесінде,
заттардың жағдайының біртіндеп өзгеруі арқылы жүзеге асырылады.
Күнделікті адам санасында кеңістік пен уақыт үғымы қалыпты тұрмыстық
жағдай ретінде есептелінеді, материя уақыт пен кеңістіктің аумағында
қарастырылып, материя жоғалған күйде де, олар сақталып қала береді деп
есептеледі [2-14].
Мұндай көзқарас кеңістік пен уақытқа абсолютті мән береді, және бұл
жайлы И.Ньютонның Табиғат философиясының математикалық бастамалары атты
еңбегінде нақты анықтама берілді. Бұл жерде абсолютті кеңістік пен уақыт
жаратылыстың материалдық процестерден тәуелсіз өзін-өзі басқаратын
элементтері ретінде қарастырылады. Бұл концепция қара жәшік концепциясы
деп аталады.
Бірақ оларда субстанцияның ең маңызды қасиеті - әр түрлі денелерді
тудыру қабілеті жоқ. Сонымен қатар басқа концепциялар да бар (Беркли, Мах,
Авенариус тағы басқа) олар кеңістік пен уақытты адам санасына тәуелді етіп
көрсетеді. Кеңістік пен уақыт мәселелері жақыннан әсер ету және алыстан
әсер ету концепцияларымен тығыз байланысты. Алыстан әсер ету гравитациялық
және электр күштерінің бір сәтте абсолюттік кеңістік арқылы таралуы, ең
соңында өзінің көздеген мақсатына құдайдың бұйрығымен жетеді. Ал жақыннан
әсер ету концепциясы (Декарт, Гюйгенс, Френель, Фарадей) кеңістікті зат пен
эфирдің жалғасы ретінде қарастырады.
Өзара әрекеттесу мен кеңістікті түсіну классикалық физиканың
шеңберінде дами отырып, XX ғасырда одан әрі дамыды.
Кеңістік пен уақыт қайтадан материя атрибуты ретінде оны анықтайтын
байланыстары және өзара байланыстары арқылы түсіндіріледі [3-16].
Уақыт пен кеңістіктің қазіргі кездегі түсінігі А.Эйнштейннің
салыстырмалылық теориясы арқылы түсіндіріледі.
Салыстырмалылық теориясының ең алғашқы бастамасы салыстырмалылық
принципі болып табылады.
XX ғасырдың басында салыстырмалылық принципі оптика мен физикаға және
физиканың басқа салаларына қатысты екендігі белгілі болды. Салыстырмалылық
принципі өзінің мәнін кеңейтіп, мынадай анықтамаға ие болды: оқшауланған
материалдық жүйеде кез-келген процесс бірдей жүреді, және ол жүйе бір
қалыпты түзу сызықты қозғалыс жағдайында болуы керек. Немесе физиканың
заңдары барлық инертті жүйелерде бірдей формаға ие.
Бір инертті жүйеден келесіге ауысу Лоренц қайта өзгертулері арқылы
жүзеге асырылды. Бірақ жарық жылдамдығы түрақтылығы туралы мәліметтер
қайтадан жаңа түсініктерді қажет ететін мәселелерге әкеліп тіреді. 1904
жылы X.Лоренц қозғалыстағы дене өзінің қозғалыс бағыты бойынша
қысқаратындығын және әртүрлі жүйелерде байқалатын уақыт аралықтары
өлшенетінін айтты. Бірақ, келесі жылы А.Эйнштейн Лоренц қайта құруларындағы
байқалатын уақытты нақты уақыт ретінде қарастырды [4-7].
Жалпы салыстырмалылық теориясында кеңістік - уақыт қатынастарының
материалдық процестерге қатысының жаңа жақтары ашылды. Жалпы
салыстырмалылық теориясы инерциялық және гравитациялық массалардың
эквиваленттік принципінен шығады. Атап айтқанда, массалардың эквиваленттік
принципінің негізінде салыстырмалылық принципі қалыптасты, ол жалпы
салыстырмалылық теориясында табиғат заңдарының инварианттылығын бекітті.
Салыстырмалылық теориясы кеңістіктің ауырлық күшінің әсерінен
майысатындығын және уақыт барысының күшті гравитациялық өрістерде
баяулайтынын анықтады.
Жалпы салыстырмалылық теориясының фантастикалық болжамдарының бірі -
өте күшті тартылыс өрісінде уақыттың толық тоқтайтындығы туралы. Тартылыс
күші артқан сайын уақыттың баяулауы да күшейе түседі. Уақыттың баяулауы
жарықтың гравитациялық қызыл орын ауыстыруы арқылы байқалады да, толқындар
үзындығы артқан сайын оның жиілігі азая береді. Белгілі бір жағдайда толқын
үзындығы шексіздікке, ал жиілігі нөлге үмтылады.
Салыстырмалылық теориясы уақыт пен кеңістіктің бірлігін көрсетті,
кеңістік-уақыттық төртөлшемдік контимум туралы түсінік қалыптасты.
Салыстырмалылық теориясы масса мен энергияны Е-МС қатынасымен
байланыстырды, мұнда С - жарық жылдамдығы.
Салыстырмалылық теориясында екі заң - зат массасының және энергиясының
сақталуы заңдары бірігіп, энергия және зат массасының сақталуы деген бір
заңға айналды [5-9].
Қазіргі кездегі жаратылыстанудағы, оның ішінде физикадағы өзекті
мәселелердің бірі - әлемдегі себептілік және себептілік қатынастар
табиғатының мәселесі. Физикада бұл мәселе обьективті заңдылықта динамикалық
және статистикалық заңдар арқылы беріледі. Бұл мәселені шешуде екі
философиялық бағыт - детерминизм және индетерминизм қалыптасты.
Детерминизм - табиғи, әлеуметтік және психологиялық құбылыстардың
обьективті себептерін жоққа шығарды.
Қазіргі кездегі физикада детерминизм идеясы обьективті физикалық
заңдылықтарды тану арқылы беріліп, іргелі физикалық теорияларға сүйенеді.
Іргелі физикалық теориялар (заңдар) физикалық заңдылықтар туралы ең
маңызды білім жиынтығын береді. Әрине, бұл білім жиынтығы ең соңғы нәтиже
деп қарастырылмайды, дегенмен бүгінгі күнде табиғаттағы физикалық
процестерді толық ашып көрсетеді.
Ғылымтанушы ғалымдар кез келген физикалық теорияның негізін үш
элемент:
1) физикалық бірліктер жиынтығы (Мысалы: Ньютон механикасында -
кординаталар, импульс, энергия, күш тағы басқа);
2)  физикалық күш түсінігі;
3)  қозғалыс теңдеуі, яғни белгілі жүйенің эволюциясын көрсететін
теңдеу құрайды деп есептейді.
Динамикалық заң дегеніміз - физикадағы обьективті заңдылықтарды сан
түрінде, физикалық бірліктер байланысы арқылы беретін заң. Динамикалық
заңдардың жиынтығын динамикалық теория деп атайды.
Тарихи түрде алғанда ондай теориялардың алғашқысы Ньютонның
классикалық механикасы [6-12].
Іргелі физикалық теориялардың ішіндегі тағы бірі - Максвелдің
электродинамикасы. Максвелл теңдеулері материяның злектромагниттік формасы
үшін қозғалыс теңдеулері болып табылады. Сонымен бірге электродинамика
құрылымы ортақ сипаттары бойынша Ньютон механикасының құрылымын анықтайды.
Динамикалық сипаттағы басқа іргелі теорияларға тұтас орта механикасы,
термодинамика және жалпы салыстырмалылық теориясы (гравитациялық теория)
жатады.
Физикадағы классикалық детерминизмнен бастарту - динамикалық заңдардың
әмбебап емес екендігін, олардан басқа табиғаттың терең заңдары - яғни, XIX
ғасырдың екінші жартысында ащылған статистикалық заңдардың бар екендігі
түжырымдалды.
Статистикалық заңдар мен теориялардың мынандай өзіндік ерекшеліктері
бар:
1. Статистикалық теорияларда кез-келген күй жүйенің ықтималды
сипаттамасын береді. Бұның өзі статистикалық теорияларда күй физикалық
бірліктер арқылы емес, бұл бірліктердің статистикалық таралуы арқылы
анықталады.
2.  Статистикалық теорияларда белгілі алғашқы нәтиже бойынша физикалық
бірліктердің шамалары емес, бұл шамалардың берілген интервал ішіндегі
ықтималды мәні анықталады.
Күйдің статистикалық теориялардағы ықтималды сипаттары ди-намикалық
теориялардағы сипаттамаларынан мүлдем өзгеше.
Статистикалық заңдар мен заңдылықтар деңгейінде біз себептілік пен
жолығамыз. Бірақ статистикалық заңдылықтардағы детерминизм табиғаттағы
детерминизм формасының ең терең түрін береді.
Статистикалық заңдар мен теориялар физикалық заңдылықтарды сипаттаудың
ең бір жетілген түрі болып табылады [7-13].
Физикада статистикалық заңдар шыға салысымен олардың динамикалық
заңдармен қатысы туралы мәселе қарастырыла бастады.
Статистикалық заңдар - заңдылықтарды сипаттаудың жаңа түрі ретінде,
алғашында классикалық механиканың динамикалық теңдеулері негізінде берілді.
Кванттық теорияның пайда болуы және дамуы біртіндеп динамикалық және
статистикалық заңдардың табиғат заңдылықтарын көрсетудегі рөлін қайта
қарауға алып келді. Сондықтан, көптеген ғалымдар: Н. Бор, В.Гейзенберг,
М.Борн, П.Ланжевен және басқалары статистикалық заңдарды алғашқы деп қарау
туралы тезис ұсынды.
Статикалық және динамикалық заңдарды қарастырған кезде біз бұл
мәселенің екі аспектісімен кездесеміз.
Бірінші аспекті бойынша, динамикалық және статистикалық заңдар
арасындағы қатынас былай беріледі: жеке обьектілердің жағдайын білдіретін
заңдар - динамикалық заңдар, ал олардың жиынтығының жағдайын білдіретін
заңдар - статистикалық заңдар ретінде қарастырылады. Классикалық механика
мен статистикалық механика арақатынасы осындай.
Екінші аспект бойынша, динамикалық және статистикалық заңдардың
арақатынасының мәселесі қарастырылады. Бұған мысал ретінде термодинамика
және статистикалық механика, Максвелдің электродинамикасы мен электрондық
теория жатады.
Дене екі жағдайда материялық нүкте деп аталады: а) дененің өлшемі осы
дене қозғалуы нәтижесінде жүрілген аралықпен салыстырғанда немесе осы
денеден басқа денелерге дейінгі ара қашықтықпен салыстырғанда өте аз болса;
б) дененің барлық нүктесі бірдей қозғалыспен сипатталған жағдайда, яғни
барлық нүктесінің кез келген мезеттегі жылдамдықтары мен қозғалыс
траекториялары бірдей болса, мұндай қозғалыс ілгерлемелі қозғалыс деп
аталады. Ілгерлемелі қозғалыс кезінде денемен байланысқан кез - келген түзу
өзіне өзі параллель орын ауыстырады. Денелердің ілгерлемелі қозғалысы
траекторияның түріне қарай екіге бөлінеді: егер траектория түзу болса, онда
түзу сызықты ілгерлемелі қозғалыс, ал траектория қисық сызық болса, онда
қисық сызықты ілгерлемелі қозғалыс деп аталады [8-15].
Ілгерлемелі қозғалыс.
Дене ілгерлемелі қозғалыс жасағанда, оның барлық нүктелерінің қозғалыс
сипаты бірдей болатындықтан, дененің орнына материялық нүктенің қозғалысын
қарастырамыз. Материялық нүкте қисық бойымен қозғалады делік (2-сурет).
Осындағы ∆l векторы орын ауыстыру болып шығады. Материялық нүктенің белгілі
бір уақыт аралығындағы орын ауыстыруы дегеніміз нүктенің бастапқы уақыт
мезетіндегі орнынан соңғы уақыт мезетіндегі орнына жүргізілген ∆r векторы
(2-сурет). 2-суреттен ∆rb=ra + ∆r бұдан орын ауыстыру векторы мынаған тең:
∆r= rb= ra .

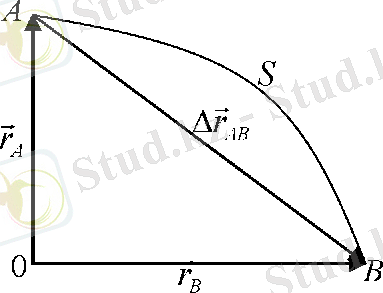
2-сурет.

Материялық нүкте траекториясының ұзындығына тең скаляр шама S жүрілген
жол деп аталады (2-сурет). Материялық нүкте түзу бойымен бір бағытта
қозғалғанда жол мен орын ауыстыру векторының модулінің мәні тең болады,
яғни S=ǀ∆rǀ, ал басқа жағдайларда орын ауыстыру модулі әрқашан жол
ұзындығынан Sǀ∆rǀ аз болады. Тіпті, шеңбер бойымен болатын немесе
тербелмелі қозғалыста орын ауыстыру модулі кейде нөлге де тең болуы мүмкін,
өйткені дене бастапқы орнына қайта-қайта оралады. Ал жүрілген жол уақытқа
байланысты кемімейтін, әрқашан оң скаляр шама.
Орын ауыстыруды осы орын ауыстыруға кеткен уақытқа бөлсек, қозғалыс
жылдамдығы шығады: v=. Бұл нүктенің АВ түзуі бойымен ∆t уақыт ішіндегі
қозғалыс жылдамдығы (2-сурет). Мұның мәні қозғалыс жылдамдығының нақты
мәніне сәйкес келмейтінін оңай байқауға болады. Алайда, егер ∆t уақыт
аралығын шексіз азайтсақ, яғни В нүктесін А нүктесіне жақындатсақ, онда ∆r
де нөлге ұмтылады, ал оның бағыты А нүктесіне жүргізілген жанама бойымен
бағытталып, жылдамдықтың мәні материялық нүктенің нақты жылдамдығы
мәнінен айырмашылығы азая береді. Сонымен, бұл жылдамдық – уақыт ∆t нөлге
ұмтылғанда , қатынасының ұмтылатын шегі: ν==.
Жылдамдық қозғалыс күйінің сандық өлшеуіші; физика тілінде айтқанда,
жылдамдық элементар орын ауыстыру векторының осы орын ауыстыруға кеткен
уақытқа қатынасына тең шама.
Траекторияның берілген нүктесіндегі жылдамдық - осы нүктеге
жүргізілген жанаманың бойымен бағытталады.
Материялық нүктенің қозғалыс жылдамдығының уақытқа байланысты өзгеруін
сипаттайтын шама - үдеу. Үдеу уақыт өтуіне байланысты жылдамдықтың модулі
мен бағытының қалай өзгеретінін көрсетеді де, сан жағынан, жылдамдық
өзгерісі векторының ∆ν осы өзгеріске кеткен ∆t уақытқа қатынасына тең
болады: a = .
Кинематикадан есеп шығарғанда, берілген траектория бойынша жолдың
ұзындығының уақытқа тәуелділігі түрі анықталады. Қозғалыс траекториясы мен
қозғалыс заңы бір-біріне байланысты емес сипаттамалар, сондықтан қандай да
болсын бір қозғалысты қарастырғанда олардың әрқайсысының ерекшеліктерін
атап айту қажет [9-5].
Траекторияның түріне қарай қозғалыс түзу сызықты қозғалыс және қисық
сызықты қозғалыс болып бөлінеді.
Қозғалыс заңдарының берілуі:
жолдың S ұзындығының t уақытқа тәуелділігін көрсететін кесте түрінде;
жолдың S ұзындығының t уақытқа тәуелділігі график түрінде;
жолдың S ұзындығының t уақытқа тәуелділігі формула түрінде беріледі.
Қозғалыс заңдарының барлығы қозғалыстың (түзу сызықты ма, жоқ әлде
қисық сызықты ма оған тәуелсіз) түріне қарамастан бірдей жазылатын
болғандықтан, бұдан былай біз орын ауыстыру мен жылдамдық модульдерінің
уақытқа байланысты өзгерістерін көрсететін қозғалыс заңдарын ғана
қарастырамыз. Ал орын ауыстыру, жылдамдық бағыттарының өзгерісін қозғалыс
траекториясы сипаттайды.
Егер қозғалыс кезінде қозғалыс бағыты (немесе жылдамдық бағыты)
өзгермесе, онда ол түзу сызықты қозғалыс деп аталады.
Егер қозғалыс кезінде қозғалыс бағыты (жылдамдықтың бағыты) өзгеріп
отырса, онда мұндай қозғалыс қисық сызықты қозғалыс деп аталады.
Егер жылдамдық модулі уақыт өтуіне қарай өзгермесе, онда мұндай
қозғалысты бір қалыпты қозғалыс дейді, яғни дене тең уақыт аралықтарында
бірдей жол жүреді.
Егер тең уақыт аралықтарында жылдамдық модулі бірдей шамаларға
өзгеретін болса, онда мұндай қозғалысты бір қалыпты үдемелі қозғалыс дейді.
Жоғарыдағы анықтамаларды пайдалана отырып, жалпы физика курсында
қарастырылатын барлық күрделі қозғалыс түрлерінің сәйкес анықтамаларын
беруге болады.
Егер қозғалған дене тең уақыт аралықтарында бірдей жол жүріп (яғни
жылдамдық модулі өзгермесе) және қозғалыс бағыты өзгермесе, онда мұндай
қозғалыс бір қалыпты түзу сызықты қозғалыс деп аталады.
Қозғалыс бағыты ұдайы өзгеріп отырып, ал жылдамдық модулі тұрақты болатын
қозғалысты бір қалыпты қисық сызықты қозғалыс дейді.
Егер қозғалыс бағыты өзгермесе, ал жылдамдық модулі бойынша тең уақыт
аралықтарында бірдей шамаға өзгеріп отыратын болса, онда қозғалыс түзу
сызықты бір қалыпты үдемелі қозғалыс деп аталады.
Қозғалыс бағыты ұдайы өзгеріп отырып, ал жылдамдық модулі тең уақыт
аралықтарында бірдей шамаға өзгеретін қозғалыс қисық сызықты бір қалыпты
үдемелі қозғалыс деп аталады [10-15].
Қозғалыс заңдарын қарастырған кезде дененің кез келген траектория
бойымен болатын (мысалы, судың, өзеннің бұралаңдаған арнасымен ағысы)
қозғалысының жолы мен жылдамдығының мәндері қажет болады. Сондықтан олардың
мәндерін шартты түрде бір бағытта мысалы, ағыс бағыты бойынша оң деп, ал
керісінше, ағыс бағытына қарсы болса, теріс деп аламыз.
Материялық нүкте траектория бойымен тең уақыт аралықтарында бірдей жол
жүрсе немесе уақыт өтуіне қарай жылдамдық модулі өзгермесе, ондай қозғалыс
бір қалыпты қозғалыс деп аталады, яғни ν= .

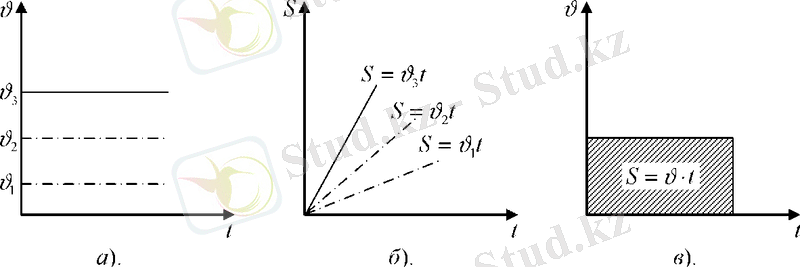
3-сурет.

Олай болса,қозғалыс кезінде жүрілген жол жылдамдық модулін уақытқа
көбейткенге тең: S=ν·t. Дененің t уақыт мезетіндегі координаты x=x0+ν·t,
мұндағы x0 дененің t=0 бастапқы мезеттегі координаты. 3-суретте бір қалыпты
қозғалыстың жылдамдығы мен жолының уақытқа байланысты сызбасы көрсетілген.
Жылдамдық неғұрлым көп болса, жолдың уақытқа байланысты сызбасындағы
(3, б-сурет) түзудің көлбеулік бұрышы соғұрлым тік болады.
x=0 болса, онда координат пен жолдың сызбалары сәйкес келеді.
Халықаралық бірліктер жүйесінде жылдамдық бірлігіне бір секундтағы метр
алынған. Алайда, жүйеден тыс бірліктер де қолданылады, мысалы бір сағаттағы
километр (кмсағ), бір секундтағы километр (кмс) және т.б [12-17].

1.2 Санақ денесі. Санақ жүйесі. Жылдамдық. Үдеу

Айнымалы қозғалыс деп уақыт өтуіне қарай жылдамдық модулі өзгеріп
отыратын немесе материялық нүкте траектория бойымен тең уақыт аралықтарында
әр түрлі жол жүретін қозғалысты айтады.
Айнымалы қозғалыстың νорт орташа жылдамдығы дененің ∆t уақыт
аралығында жүрген ∆S жолын осы ∆t уақыт аралығына бөлгенге тең:
νорт=.
Орташа жылдамдық - скаляр шама. Мысалы, поездың, автомобильдің, жаяу
адамның және т.б. орташа жылдамдығы туралы айтылады.
Материялық нүкте қозғалысы әр уақыт мезетінде, яғни басқаша айтқанда,
траекторияның әр нүктесінде лездік жылдамдық деген физикалық шамамен
сипатталады. Лездік жылдамдық сан жағынан ∆t уақыт аралығын шексіз
азайтқанда орташа жылдамдықтың ұмтылатын шегіне тең.
Лездік жылдамдық - вектор, ол қозғалыс траекториясына жүргізілген
жанама бойымен бағытталады (4-сурет). Вектор болғандықтан жылдамдықтың
бірыңғай бағыты немесе бірыңғай модулі ғана өзгеріп қоймай әрі бағыты, әрі
модулі бір мезгілде өзгеруі мүмкін.

4-сурет.

Жылдамдық модулі тұрақты болып ǀνǀ=const, ǀν1ǀ=ǀv2ǀ ал оның бағыты
уақытқа байланысты өзгеріп отыратын жағдайды қарастырайық (5, а-сурет),

a) b)
c)

5-cурет.

Жылдамдықтың ∆t уақыт аралығындағы Δv өзгерісі ∆ν=ν2 - ν1 немесе ( ν2
= ν1 - ∆ν) болғандықтан, ∆ν жылдамдықтың бағыты жағынан болатын өзгерісін
көрсетеді (5, б-сурет). Шексіз аз уақыт аралығындағы жылдамдық бағыты
өзгерісінің осы уақытқа қатынасымен сипатталатын физикалық шаманы нормаль
үдеу дейді, яғни:
ar=

Сонымен, нормаль үдеу жылдамдық бағыты өзгерісін сипаттайды [13,18].
Енді уақытқа байланысты жылдамдық модулі өзгеріп, ал жылдамдық бағыты
өзгермейтін жағдайды қарастырайық:

a) b)

6-сурет

Жылдамдықтың уақыт аралығындағы өзгерісі Δv=v2 - v1. Қозғалыс бағыты
өзгермейтіндіктен, ∆ν жылдамдықтың абсолют шамасының (модулінің) өзгерісін
көрсетеді. Шексіз аз уақыт аралығындағы жылдамдықтың модулі өзгерісінің осы
уақыт аралығына қатынасына тең физикалық шама тангенциал (жанама бойымен
бағытталған) үдеу деп аталады.

ar=.

Сонымен, тангенциал үдеу жылдамдықтың модулінің өзгерісін сипаттайды.

а). б).
в)

7-сурет.
Енді, жылдамдықтың уақытқа байланысты бағыты да, модулі де өзгеретін
жағдайды қарастырайық (7, а-сурет).

Жылдамдықтың ∆t уақыт аралығындағы өзгерісі Δv=v2 – v1. .12,б-
суретте OB=OA кесінділері салынған, олар сан жағынан ν1 жылдамдықтың
модуліне тең, олай болса, суреттегі ∆νn жылдамдықтың бағытының өзгерісін
сипаттайды да, ал ∆νt- жылдамдықтың модулінің өзгерісін көрсетеді. Олай
болса, ∆ν=νn + νt , бұдан

a=.
Дене қозғалысының жылдамдық векторы өзгерістерінің сандық сипаттамасы
болып табылатын физикалық шама толық үдеу деп аталады. Үдеудің СИ
жүйесіндегі өлшем бірлігі квадрат секундтағы метр (мс ).
Бірнеше қозғалысқа қатысатын материялық нүктенің жылдамдықтары, сондай-
ақ үдеулері векторларды қосу ережесімен орындалады.
Егер материялық нүкте Х өсі бойымен қозғалса, онда

v=
x=(болады.
Сонымен, егер
және болса, онда қозғалыс бір қалыпты түзу сызықты;
, және болса, онда қозғалыс түзу сызықты бір қалыпты
үдемелі;
және, ал болса, онда қозғалыс бір қалыпты қисық сызықты
деп аталады [14].

1.3 Бір қалыпты айнымалы қозғалыс

Тең уақыт аралықтары ішінде жылдамдық модулі бірдей шамаға өзгеріп
отыратын қозғалысты бір қалыпты айнымалы қозғалыс дейді.
Дене бір қалыпты айнымалы қозғалыс жасағанда оның үдеуі тұрақты
болады:
ar= (1)
Мұндағы v0- дененің бастапқы жылдамдығының мәні; t - қозғалыс
бақыланғаннан бергі уақыт; v - жылдамдықтың t уақыт мезетіндегі мәні, ол
бағыты жағынан бастапқы жылдамдықпен бағыттас болса оң, ал керісінше, оған
қарсы бағытталса - теріс болады. Бір қалыпты айнымалы қозғалыстың уақыт
мезетіндегі жылдамдығы:
v = v0 + a · t (2)
Материялық нүктенің кез - келген траекториямен болатын қозғалыс
жылдамдығының уақытқа байланысты өзгерісін тік бұрышты координаттар
жүйесінде көрсеткен қолайлы. Жоғарыда айтылған бойынша, оң бағыт ретінде
бастапқы жылдамдықтың берілген траекториядағы бағыты алынады. Материялық
нүктенің бір қалыпты айнымалы қозғалыс жылдамдығы модулінің уақытқа
байланысты сызбасы түзу сызық болады (8-сурет).

а) .б)
. в).

8-сурет.

Осы түзудің уақыт өсімен жасайтын бұрышының тангенсі материялық
нүктенің a үдеуіне тең (a=tgα). Егер үдеу оң болса, үдеудің бағыты
бастапқы жылдамдықпен бағыттас, онда tgα 0 (8, а, 8, б-сурет), ал егер
үдеу теріс болса, онда tgα 0, олай болса, бұл - кейбір уақыт
мезеттерінде жылдамдықтың мәні v0 бастапқы жылдамдықтан кем болуы мүмкін
деген сөз (8, в-сурет).
Ал енді, бір қалыпты үдемелі қозғалысты (a 0) қарастырайық.
Қозғалысқа кеткен уақытты бірнеше аралыққа бөлейік (9-сурет). Жүрілген
жолды шамамен былай есептеуге болады: S=vорт∆t1+vорт2∆t2+vорт3∆t3 , ∆t1,
∆t2 және ∆t3 уақыт аралықтарында дене сәйкес vорт1, vорт2 және vорт3
орташа жылдамдықпен қозғалды деп есептесек, онда оның Δt уақытта жүрген
жолы S1=∆t1 · vорт 1 , ал ∆t2 уақыт аралығында S2=∆t2 · vорт2 , сондай-ақ
∆t3 уақытта S3=vорт3 · ∆t3 болады. Бұл теңдіктің оң жағы жоғары жағынан
abcdf сынық сызығымен шектелген тік төртбұрыштардың аудандарының
қосындысына тең (S=S1 + S2 + S3).

9-сурет.

Уақыт аралығы көбейген сайын (яғни ∆t уақыт аралығы азайған сайын) бұл
сынық сызық AB түзуімен дәл келеді. Ендеше, дененің жүрген жолы жоғарыдан
АВ түзуімен, ал төменнен t уақыт өсімен шектелген трапецияның ауданына тең
болады:
S = v0 · t +
мұндағы, - материялық нүктенің уақыт ішіндегі орташа жылдамдығы.
Жылдамдықтың (2) өрнегін осы (3) теңдеуге қойып,
S = (4)
аламыз [15,17].
Материялық нүктенің кез келген уақыт мезетіндегі координаты үшін
x = x0 + S = x0 + v0 · t +
(5)
мұндағы x0 - дененің бастапқы уақыт мезетіндегі координаты.
Егер (2) және (4) теңдеулерден t уақытты аластасақ, онда материялық
нүктенің бір қалыпты айнымалы қозғалысы жылдамдығы мен жүрген жолының
арасындағы байланысты аламыз, яғни:
v= (6)
Егер v0 = 0 болса, онда v = a · t, ал бұдан
S =
(7).
Жүрілген жолды a 0 болған жағдайда (7) формуламен табуға болады, ал
a 0 болғанда оны қолдануға болмайды.

10-сурет.

Ал енді үдеуі бастапқы қозғалыс бағытына ( v0 жылдамдыққа) траектория
бойымен қарсы бағытталған бір қалыпты айнымалы қозғалысты қарастырайық (10-
сурет). Сызбадан t1 уақыт мезетіне дейінгі (v1= 0 ) орташа жылдамдық
vорт= екенін көруге болады. Бұл уақыт ішінде жүрілген S1 жолды
есептейік:
S1 = v0 · t1 + ,
мұндағы t1 = t1 0.Ол v1 = v0 + a · t1 = 0 өрнегінен табылады.
Егер материялық нүкте жылдамдығы нөлге тең болған мезеттен кейін де
сол үдеумен қозғалған болса (енді қарама-қарсы бағытта), онда (4) формула
бойынша S 0 болады. Жүрілген жол уақыт өтуіне қарай ылғи өсіп отырады,
сондықтан бұл жағдайда барлық жолды есептеу үшін (4) формула жарамайды.
Барлық жолды S1 және S2 аудандардың айырмасы емес, қосындысына тең деп S2
= алу керек. Mағынасы тек t ≥ t1 шарт орындалғанда ғана болады,
сондықтан a 0 және t t1 жағдайда жүрілген жол мына формуламен
есептеледі:
S = S1 + S2 = v0t1 + (8).
Ал,материялық нүктенің координаты x = v0 · t + формуладан
анықталады.
Координат пен жолдың уақытқа тәуелділігі сызбасы a 0 болғанда бірдей
болады да, ал a 0 жағдайда қозғалыс жылдамдығы нөлге тең ( t = t1 мезетке
дейін) болғанға дейін ( v1 = 0, 11,б-сурет), сәйкес бірдей болып, ал одан
әрі қарай жол қисығы жоғары (өйткені ылғи да өсіп отырады), ал координат
қисығы төмен қарай (11, в-сурет) бұрылады.
Бір қалыпты үдемелі қозғалыс мысалдарының бірі - еркін түсу. Дененің
тек қана ауырлық күшінің әсерімен болатын қозғалысын еркін түсу дейді.
Ауырлық күшінің Жер бетіне жақын нүктелеріндегі мәні тұрақты деп алынады.
Еркін түсу үдеуі g әрпімен белгіленеді ( g = 9,8 мс2 ).

а) .б) . в).

11-cурет.

Кинематикада қозғалыстың тәуелсіздігі принципі кең орын алады, ол
былай тұжырымдалады: егер материялық нүкте бірден бірнеше қозғалысқа
қатынасатын болса, онда оның осы қозғалысының қорытқы орын ауыстыруы әрбір
жеке қозғалыстың орын ауыстыруларының векторлық қосындысына тең болады
[16].
Кинематикадан есеп шығарғанда, көбінесе, дененің бірден екі қозғалысқа
қатынасуы жиі кездеседі. Мысалы, көкжиекке бұрыш жасай лақтырылған дене екі
түрлі: 1) горизонталь бағытта бір қалыпты; 2) вертикаль бағытта үдемелі
қозғалады.
Кинематика бөлімінде механикалық қозғалыстың тек қана уақытқа
байланысты өзгерістерін қарастырдық. Бірақ ол қозғалыстың себептерін және
өзгеріс әдістерін ескермегендіктен механиканың негізгі бөлімі бола алмайды,
сондықтан да механиканың негізі динамика болып табылады.
Динамика денелердің әсерлесу кезіндегі қозғалысының өзгерісін
зерттейді. Ньютонның үш заңы негізгі заңдар болып алынады. Бұл заңдар
көптеген тәжірибелердің қорытындысына негізделген.

2 Ньютонның заңдары
2.1 Ньютонның бірінші заңы
Дене траектория бойынша қозғалғанда оның жылдамдығы v модулі және
бағыты бойынша өзгереді. Бұл дененің a үдеумен қозғалатынын білдіреді.
Кинематикада дененің үдеуін тудыратын физикалық себебі туралы сұрақ
қойылмайды. Тәжірибе көрсеткендей, дене жылдамдығының кез - келген өзгерісі
басқа денелердің әсерімен болады. Динамика бір дененің екінші денеге әсерін
денелердің қозғалыс сипаттамасын анықтайтын себеп ретінде қарастырады.
Денелердің әсерлесуі деп денелердің әрқайсысының қозғалысының әсерін
айтады. Денелердің әсерлесу заңдарын зерттейтін механиканың бөлімін
динамика деп атайды. Динамика заңдарын ұлы ғалым И. Ньютон ашқан. Ньютон
тұжырымдаған динамиканың үш заңы классикалық механиканың негізі жатыр.
Ньютон заңдарын тәжірибелік деректерді жалпылауы ретінде қарастыруға
болады. Классикалық механиканың қорытындылары жарық жылдамдығынан бірнеше
есе аз жылдамдықпен қозғалатын денелер үшін дұрыс. Ең қарапайым механикалық
жүйе – бұл ешқандай дене әсер етпейтін оқшауланған дене болып табылады.
Қозғалыс және тыныштық салыстырмалы болғандықтан, әр түрлі санақ
жүйелерінде оқшауланған дененің қозғалысы әр түрлі болады. Бір санақ
жүйесінде дене тыныштықта болуы немесе тұрақты жылдамдықпен қозғалуы
мүмкін, ал басқа жүйеде осы дене үдеумен қозғалуы мүмкін.
Ньютонның бірінші заңы (немесе инерция заңы) әр алуан жүйелердің
санақ жүйелерінен инерциалдық жүйелердің класын бөліп шығарады [17-20].
Ілгерілемелі қозғалатын денелер өзінің жылдамдығының модулін және
бағытын сақтайтын санақ жүйелері бар болады. Басқа денелердің әсері
болмағанда өзінің жылдамдығын сақтайтын дененің қасиетін инерция деп
атайды. Сондықтан Ньютонның бірінші заңы инерция заңы деп атайды. Алғаш
инерция заңын Г.Галилей тұжырымдаған (1632 ж). Ньютон Галилейдің
қорытындыларын жалпылап, оларды қозғалыс заңдарының қатарына қосты. Ньютон
механикасында денелердің өзара әсерлесу заңдары инерциалдық санақ жүйелері
үшін тұжырымдалады. Жер бетіне жақын қозғалысты сипаттауда Жермен
байланысты санақ жүйелерін инерциалды деп санауға болады. Алайда тәжірибе
дәлдігін жоғарылатқанда, Жердің өз осі бойымен айналғанына байланысты
инерция заңынан ауытқулар пайда болады. Жермен байланысты инерциялы емес
жүйені көрсететін механикалық тәжірибенің мысалы ретінде Фуко маятнигін
келтіруге болады. Осылай жеткілікті ұзын жіпке ілінген және тепе-теңдік
қалыпқа жақын тербеліс жасайтын массивті шар аталады. Егер Жермен
байланысты жүйе инерциалды болса, онда Фуко маятнигінің тербеліс жазықтығы
Жерге қатысты өзгеріссіз қалар еді. Шын мәнінде маятник тербелісінің
жазықтығы Жер айналысының салдарынан бұрылады, және маятник траекториясының
Жер бетіндегі проекциясы розетка түрінде болады (2.1-сурет).

2.1-сурет. Фуко маятнигінің тербеліс жазықтығының бұрылуы

Жоғары дәлдікпен басы Күн центрінде, ал осьтері алыс жұлдыздарға
бағытталған гелиоцентрлік санақ жүйесі (немесе Коперник жүйесі) инерциялық
жүйе болып табылады. Бұл жүйені Ньютон бүкіл әлемдік тартылыс заңын ашқанда
қолданды (1682 ж). Инерциялық жүйелер шексіз көп. Тұрақты жылдамдықпен түзу
сызықты жолмен келе жатқан поезбен байланысты санақ жүйесі, Жермен
байланысты санақ жүйесі сияқты да жуық шамамен инерциялық жүйе болып
табылады. Барлық инерциялық жүйелер бір-біріне қатысты бірқалыпты және
түзусызықты қозғалатын жүйелер класын құрайды. Қандай да бір дененің әр
түрлі инерциялық жүйелердегі үдеулері бірдей. Инерциялық санақ жүйесіндегі
жылдамдықтың өзгеру себебі – оның басқа денелермен әсерлесуімен байланысты.
Басқа денелердің әсеріндегі дене қозғалысының сандық сипаттамасын беру үшін
екі жаңа физикалық шаманы – дененің инертті массасын және күшті енгізу
қажет [18-21].
Масса – дененің инерттілігін сипаттайтын қасиеті. Қоршаған денелер
жағынан бірдей әсерінен бір дене өзінің жылдамдығын тез өзгертуі мүмкін, ал
басқа дене осы жағдайда біршама ақырын өзгертеді. Екінші дененің бірінші
денеге қарағанда инерттілігі үлкен, немесе басқа сөзбен айтқанда, екінші
дененің массасы көбірек деп айту қабылданған.
Егер екі дене бір бірімен әсерлессе, онда екі дененің де жылдамдығы
өзгереді, яғни өзара әсерлесу нәтижесінде екі дене де үдеу алады. Берілген
екі дененің үдеулерінің қатынасы кез келген жағдайда тұрақты болады.
Физикада әсерлескен денелердің массалары олардың үдеулеріне кері
пропорционал болатыны қабылданған:

Бұл қатынаста a1 және a2 шамаларын a1 және a2 векторларының ОХ осіне
проекциясы ретінде қарастыру қажет (2.2.сурет). Формуланың оң жағындағы
минус таңбасы әсерлескен денелердің үдеулері қарама-қарсы бағытталатынын
көрсетеді. Халықаралық бірліктер жүйесінде (СИ) масса килограммен өлшенеді.
Кез келген дененің массасы тәжірибеде эталон массасымен салыстырумен
анықталады ( mэт.= 1кг ).m1 = mэт = 1 кг. болсын. Онда
m2 =

2.2.-сурет. Екі дененің массасын салыстыру.
дененің массасы – скаляр шама. Тәжірибе көрсеткендей, егер массалары
m1 және m2 екі денені біріктірсе, онда құрама дененің массасы m , m1 және
m2   массаларының қосындысына тең:
m = m1 + m2.
Массалардың мұндай қасиеті аддитивтілік деп аталады.
Күш – бұл денелердің өзара әсерлесуінің мөлшерлік өлшемі. Күш дене
жылдамдығының өзгеруінің себебі болып табылады. Ньютон механикасында
күштердің әр түрлі себебі болуы мүмкін: үйкеліс күші, ауырлық күші,
серпімділік күш, т.б. Күш – векторлық шама. Денеге әсер ететін барлық
күштердің векторлық қосындысы тең әсерлі күш деп аталады. Күшті өлшеу үшін,
күш эталонын және басқа денелерді осы эталонмен салыстыру тәсілін анықтау
қажет. Күш эталоны ретінде белгілі ұзындыққа дейін созылған серіппені алуға
болады.

2.3.-сурет. F күшін эталонмен салыстыру. F = F0
Тағайындалған созуы кезінде серіппенің ұшына бекітілген денеге әсер
ететін күштің модулі F0 күш эталоны деп аталады. Басқа денелерді эталонмен
салыстыру тәсілі: егер дене өлшенетін F күшінің және F0 эталон күшінің
әсерінен тыныштықта тұрса, онда күштер модулі жағынан тең (2.3. сурет):
F = F0
Егер өлшенетін F күші модулі бойынша эталон күшінен үлкен болса, онда
екі эталон серіппені параллель қосуға болады (2.4.-сурет). Бұл жағдайда
өлшенетін күш 2F0-ге тең. Дәл сол сияқты, 3F0, 4F0, т.с.с. күштері
өлшенеді.

2.4. F күшін F = 2F0 эталонмен салыстыру.

2F0-ден кіші күштерді өлшеу 2.5-суретте көрсетілген схема бойынша
орындалуы мүмкін.

2.5-сурет. F күшін F = 2F0 cos α эталонмен салыстыру.

Халықаралық бірліктер жүйесінде эталон күші ньютон (Н) деп аталады.
Практикада барлық өлшенетін күштерді эталон күшімен салыстырудың
қажеті жоқ.

2.6.-сурет. F = - Fсер. тепе-теңдігі кезінде серіппенің созылуына
байланысты күшті өлшеу.

Күшті өлшеу үшін, жоғарыда сипатталған тәсілмен калибрленген серіппені
қолданады. Осындай калибрленген серіппелер динамометрлер деп аталады. Күш
динамометрдің созылуымен өлшенеді (2.6.-сурет).
Бұл заңда барлық материалдық обьектілерге ортақ қасиет – тыныштық
күйін немесе бірқалыпты түзу сызықты қозғалысын сақтау туралы айтылады.
Яғни, кез келген дене өзінің тыныштық күйін немесе бірқалыпты және түзу
сызықты қозғалысын басқа денелер әсер еткенге дейін сақтайды [19-23].
Егер қозғалысты санау жүйесімен байланыстыратын болсақ, онда қозғалушы
дене әсер етуші күштен бөлек және санау жүйесімен байланысты бірқалыпты
және түзу сызықты қозғалыста болады. Денеге ешқандай күш әсер етпесе,
немесе әсер етуші күштер қосындысы нөлге тең болса, онда дене өзінің
бастапқы тыныштық күйін немесе бірқалыпты түзу сызықты қозғалысын
сақтайды. Материалдық денелердің мұндай қасиетін инерциялық деп атайды.
Сондықтан да Ньютонның бірінші заңы, әдетте инерция заңы деп аталады.
Инерция құбылысы бірден пайда болмай әсер етуші күштің әсерінен белгілі бір
уақыттан кейін пайда болады.
Егер денелерде инерциялық қасиет болмаса, онда оның қозғалысы үдеуді
сипаттамай, тек сол уақыттағы жылдамдықтың шамасын ғана көрсетеді.
Инерциялық қасиет микроскопиялық денелер сияқты микроскопиялық
денелердің бөлщектеріне де тән. Сондықтан инерция денелер қозғалысының
түріне байланыссыз обьективті түрде қалыптасқан және барлық физикалық
денелерге тән қасиет. Ньютонның екінші заңын қарастырудың алдында
күш,салмақ және масса ұғымдарын еске түсірейік. Күш деп денелердің өзара
әсерлесуінің нәтижесінде бір-біріне үдеу беруін айтамыз. Денелердің өзара
әсері бір-біріне тек үдеу беріп қоймай, бір-бірінің көлемі мен пішінін де
өзгерте алады. Демек, дене бөлшектерінің орын ауыстыруы пайда болады. Міне,
осы дене бөлшектерінің бір-бірімен салыстырғанда орын ауыстыруын дененің
деформациясы деп атайды [20-26].
Күш- векторлық шама. Өлшем бірлігі –1 Н ( Ньютон).
Дененің жерге тартылуы кезінде оған қарсы әсер ететін екінші денеге
түсетін күшті салмақ дейді. Масса-инерттіліктің сандық өлшеуіші.
Жаратылыстану ғылымдарының, әсіресе физика тәжірибелерінің нәтижелері
материя бір түрден екінші түрге ауысқанда сақталу заңы орындалатынын және
масса болатынын көрсетті. Мысалы, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.