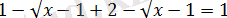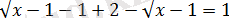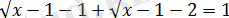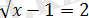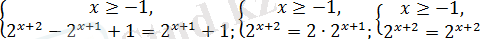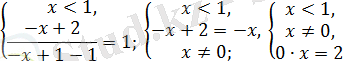Нақты сандар модулінің қасиеттері және модульді теңдеулерді шешу әдістері


Мазмұны
Кіріспе . . . 3
1. Нақты санның модулі және оның қасиеттері . . . 5
- Модульдің анықтамасы . . . 5
1. 2 Модульдің қасиеттері . . . 5
1. 3 Модульдің қасиеттерін қолданып шығарылатын есептер . . . 7
2. Модуль ішінде айнымалысы бар теңдеулер . . . 10
2. 1
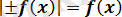 түріндегі теңдеулер . . . 10
түріндегі теңдеулер . . . 10
2. 2
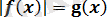 түріндегі теңдеулер . . . 10
түріндегі теңдеулер . . . 10
2. 3
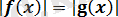 түріндегі теңдеулер . . . 14
түріндегі теңдеулер . . . 14
2. 4
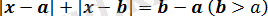 түріндегі теңдеулер . . . 15
түріндегі теңдеулер . . . 15
2. 5 Тұжырымдар және олардың дәлелдеулері, оларға келтірілген
мысалдар . . . 49
3. Модуль ішінде белгісіз айнымалысы теңдеулерді графикалық әдіспен
шешу . . . 59
3. 1 Алгебралық және графикалық әдістердің ерекше жағдайлары . . . 59
3. 2 Графикалық әдіспен мысалдарды шығару . . . 59
Тапсырмалар . . . 63
Қорытынды . . . 68
Қолданылған әдебиеттер . . . 69
Кіріспе
Тақырыптың өзектілігі: модуль түсінігі мектептегі математика курсының әр түрлі бөлімдерінде ғана емес ЖОО-нда оқылатын жоғарғы математика курсында, физикада және техникалық ғылымдарда кеңінен қолданылады. Мысалы: Механика және геометрияда вектор және оның ұзындығы (вектор модулі) түсініктері оқылады. Математикалық талдауда санның абсолютті ұзындығы түсінігі шек, шектік функция және т. б.
Модуль түсінігімен оқушылар 6-сыныптан бастап таныса бастайды. Ал дәл осы модуль ішінде айнымалысы бар теңдеулер 11-сынып оқулығында берілген және ол жылдық жоспар бойынша төртінші тоқсанда өткізілуге жоспарланған. Яғни, оқушылардың ҰБТ-ге қызу дайындалатын кезеңі, бұл дегеніміз осы тақырыпқа кездескен есептерді тез және оңтайлы әдіспен шешуді үйретуде өз септігін тигізетіні анық.
Тақырыптың мақсаты:
- жалпы модульдер туралы білімді жетілдіру;
- модульдің барлық қасиеттерін толыққанды, терең қолдану;
- ҰБТ тапсырмасында кездесетін модульмен берілген есептерді ыңғайлы әдіспен, жылдам шығаруға бейімдеу.
Зерттеу пәні: Модульмен берілген есептер.
Зерттеу объектісі: модульмен берілген әр түрлі есептерді (мектеп курсындағы күрделі, ҰБТ-де кездесетін есептер) шығару.
Дипломдық жұмыстың міндеттері:
- Модульдермен берілген есептер қарастырылатын ғылыми- математикалық әдебиеттерге талдау жасау;
- Модульдермен берілген әр түрлі есептерді шешу әдістерін қарастыру;
- Берілген жұмысқа қатысты комплексті есептерге талдау жасау.
Дипломдық жұмыс 3 бөлімнен тұрады:
Бірінші бөлімде модульдің анықтамалары, оның геометриялық интерпретациясы, абсолютті ұзындық қасиеттері келтірілген. Модульді қолданып, анықталу облысы бірдей теңдік пен теңсіздіктің кез келген жүйесін бір салыстыру түрінде алуға болатыны мысал арқылы көрсетілген. Модуль қасиеті, теңдік немесе абсолютті ұзындық белгісіне ие теңдікке мысал ретінде есептеу келтірілген
Екінші бөлімде модульдерге қолданылатын теңдеулер түрлері.
1) Модульмен берілген қарапайым теңдеудер:
1. 1
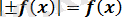 түріндегі теңдеулер
түріндегі теңдеулер
1. 2.
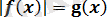 түріндегі теңдеулер
түріндегі теңдеулер
1. 3
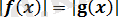 түріндегі теңдеулер
түріндегі теңдеулер
1. 4
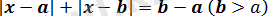 түріндегі теңдеулер
түріндегі теңдеулер
Үшінші бөлімде абсолюттік ұзындық белгісі бар теңдеулерді графикалық жолмен шешу тәсілдері келтірілген, модульдермен берілген теңдеулер кейбір жағдайларда алгебралық шешіміне қарағанда қолайлырақ болады.
Абсолютті ұзындықтың түсінігімен байланысты тестілік есептерді шешу мысалдары келтірілген. «стандартты» есептердің шешімімен қатар, параметрі бар есептердің де шешімдері келтірілген Олардың шешімінде қандай да бір шешімдердің комбинациясын алу керек. Кейбір есептер үшін бірнеше шешу әдістері келтірілген, кейде шешу процесінде туындайтын қателіктер көрсетіледі. Барлық есептер үшін жылдамдығы бойынша ең тиімді шешімдер көрсетілген.
- Нақты санның модулі және оның қасиеттері.
1. 1 Нақты санның модулінің анықтамасы
Анықтама.
Нақты санның модулі (абсолютті шамасы) деп (
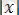 белгіленуі) егер ол сан теріс болмаса осы санның өзі аталады, егер ол теріс болса, онда қарама-қарсы таңбасымен алынған осы сан аталады.
белгіленуі) егер ол сан теріс болмаса осы санның өзі аталады, егер ол теріс болса, онда қарама-қарсы таңбасымен алынған осы сан аталады.
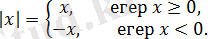
Нақты санның модулінің геометриялық мағынасын қарастырайық.
Бұл сан координатасы болып табылатын, әрбір нақты санға сандық түзуден нүкте сәйкес келеді. Бұл санның модулі - осы сандық осьтегі сәйкес нүктеден координата басына дейінгі қашықтық (1. 1. 1-сурет) .
А
нүктесінен
О
нүктесіне дейінгі қашықтық
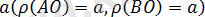 тең.
тең.
А О В
a 0 a

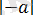
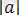
1. 1. 1-сурет
 , b
сандарының модульдерінің айырымы
, b
сандарының модульдерінің айырымы
 ,
a
және
b
,
a
және
b
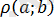 нүктелерінің ара қашықтығына сәйкес (1. 1. 2-сурет) .
нүктелерінің ара қашықтығына сәйкес (1. 1. 2-сурет) .
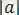
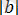
a 0 a

1. 1. 2-сурет
1. 2 Нақты санның модулінің қасиеттері
1) Модульдің квадраты модуль ішіндегі өрнектің квадратына тең, яғни кез келген
 үшін
үшін
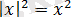 .
.
Ескерту.
Бұл формула тек солдан оңға ғана емес, яғни
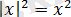 , оңнан солға да:
, оңнан солға да:
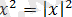 қолданылады.
қолданылады.
2) Кез келген нақты санның модулінде теріс сан бар, яғни барлық
 үшін
үшін
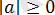 .
.
3) Нақты санның модулі осы саннан кем емес, яғни барлық
 үшін
үшін
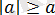 .
.
4)
 нақты санының модулі,
нақты санының модулі,
 және
және
 екі қарама-қарсы санның максимумна тең, яғни
екі қарама-қарсы санның максимумна тең, яғни
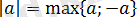 .
.
5) Олардың қосындысы осы сандардың модульдерінің қосындысына тең болғанда, сонда тек сонда ғана сандар теріс емес, яғни
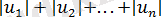 қосындысы
қосындысы
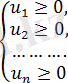 жүйесіне пара-пар.
жүйесіне пара-пар.
6) Олардың модульдерінің қосындысы осы сандардың қосындысына қарама-қайшы болғанда, сонда тек сонда ғана сандар оң емес, яғни
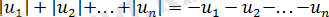 теңдігі
теңдігі
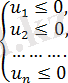 жүйесіне пара-пар.
жүйесіне пара-пар.
7) Олардың модульдерінің қосындысы олардың қосындысының модуліне тең болғанда, сонда тек сонда ғана сандар бір уақытта теріс емес және оң да емес, яғни
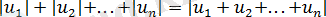 теңдігі
теңдігі
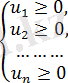 немесе
немесе
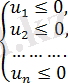 екі теңдеулер жүйесіне пара-пар.
екі теңдеулер жүйесіне пара-пар.
8) Екі санның модульдерін салыстыру олардың квадраттарының салыстыруына пара-пар, яғни келесідей пара-парлық орын алады:
 пара-пар
пара-пар

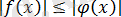 пара-пар
пара-пар
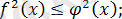
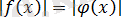 пара-пар
пара-пар
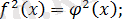
 пара-пар
пара-пар

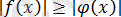 пара-пар
пара-пар
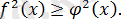
9 ) Екі нақты санның көбейтіндісінің модулі көбейткіш модулінің көбейтіндісіне тең, яғни
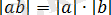 .
.
10)
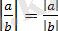 , мұндағы
, мұндағы
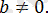
11) Кез келген бүтін
 мәні үшін
мәні үшін
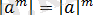 .
.
12) Егер
 - жұп сан болса, онда
- жұп сан болса, онда
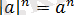 .
.
13) Түбір астындағы квадраттық сан осы санның модуліне тең:
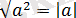 .
.
14) Екі нақты санның айырымының модулі олардың модульдерінің айырымынан кіші емес
 .
.
15) Екі нақты санның қосындысының модулі олардың модульдерінің айырымынан кіші емес
 .
.
16) Кез келген
 және
және
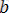 нақты сандары үшін қос теңсіздік орын алады:
нақты сандары үшін қос теңсіздік орын алады:
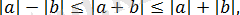

17) Кез келген
 және
және
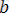 нақты сандары үшін теңсіздігі әділ:
нақты сандары үшін теңсіздігі әділ:
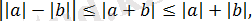
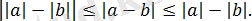
18) Кез келген
 және
және
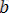 нақты сандары үшін теңдігі әділ:
нақты сандары үшін теңдігі әділ:
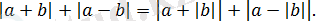
19) Кез келген нақты сандардың қосындысының модулі олардың модульдерінің қосындысынан аспайды, яғни
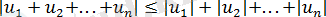 .
.
20) Екі нақты сандардың қосындысы теріс емес, ал олардың көбейтіндісі оң, сонда тек сонда ғана модульдерінің айырымының модулі осы сандардың қосындысына тең, яғни
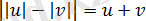 теңдігі
теңдігі
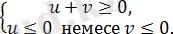
22)
 теңдеуі
теңдеуі
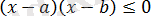 теңсіздігіне пара-пар.
теңсіздігіне пара-пар.
23)
 теңдеуі
теңдеуі
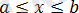 , егер
, егер
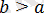 қос теңсіздігіне пара-пар.
қос теңсіздігіне пара-пар.
1. 3 Модульдің қасиеттерін қолданып шығарылатын есептер
1. 3. 1-есеп.
Өрнекті ықшамдаңыз:
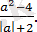
Шешуі:
Бөлшек
 -ның кез келген мәніне анықталған.
-ның кез келген мәніне анықталған.
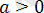 болғанда
болғанда
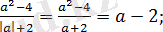
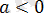 болғанда
болғанда
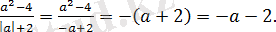
Басқада шешімдер мүмкін:
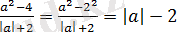 .
.
Жауабы:
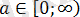 болғанда
болғанда

 болғанда
болғанда
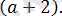
1. 3. 2-есеп.
Өрнекті ықшамдаңыз:
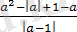 .
.
Шешуі:
Бөлшек
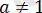 үшін анықталған. 0 және 1 сандық ості
үшін анықталған. 0 және 1 сандық ості
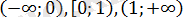 аралықтарына бөледі.
аралықтарына бөледі.
Бөлшекті әр аралықта ықшамдайық.
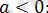
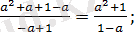
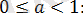
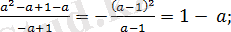

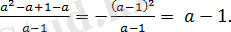
Жауабы:
 болғанда
болғанда
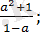
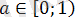 болғанда
болғанда

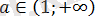 болғанда
болғанда

1. 3. 3-есеп.
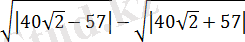 айырымы бүтін сан болады. Осы санды табыңыз.
айырымы бүтін сан болады. Осы санды табыңыз.
Шешуі:
Алғашқы өрнекті
А
әрпімен белгілейік.
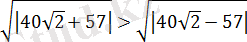 болғандықтан, онда
А
- теріс сан (және есептің шарты бойынша бүтін) .
болғандықтан, онда
А
- теріс сан (және есептің шарты бойынша бүтін) .
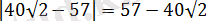 екнін ескеріп,
екнін ескеріп,
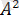 табамыз:
табамыз:
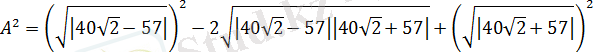
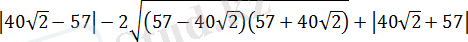
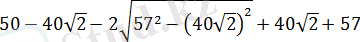
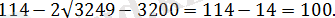
 болса, онда
болса, онда
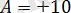 болады, бірақ жоғарда аталып өтілгендей,
болады, бірақ жоғарда аталып өтілгендей,
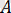 саны теріс, яғни
саны теріс, яғни
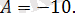
Жауабы:
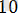
1. 3. 4-есеп.
Өрнектің ең кіші мәнін табыңыз:
 .
.
Шешуі:
Модульмен берілген көптеген есептер сияқты мына есепті де интервалдар әдісімен шығаруға болады.
Көптеген жағдайларда керек болатын тұжырымды қолдануға қолданамыз.
1. 3. 5-есеп.
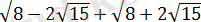 өрнегінің мәнін есептеңіз.
өрнегінің мәнін есептеңіз.
Шешуі:
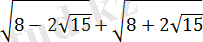
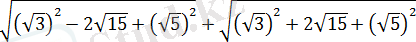
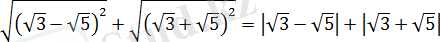
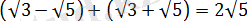 .
.
Жауабы:
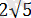 .
.
1. 3. 6-есеп.
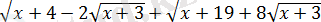 өрнегінің мәнін есептеңіз, егер
өрнегінің мәнін есептеңіз, егер
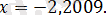
Шешуі:
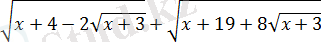
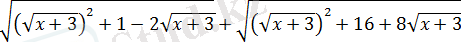
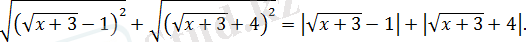
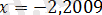 екенін ескеріп, модульдің анықтамасын қолданып
екенін ескеріп, модульдің анықтамасын қолданып
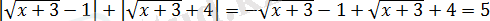 аламыз.
аламыз.
Жауабы.
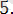
2. Модуль ішінде айнымалысы бар теңдеулер
2. 1
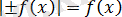 түріндегі теңдеу
түріндегі теңдеу
Берілген теңдеу
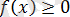 теңсіздігіне пара-пар.
теңсіздігіне пара-пар.
2. 1. 1-есеп.
Теңдеуді шешіңіз:
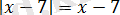 .
.
Шешуі:
Берілген теңдеу
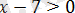 теңсіздігіне пара-пар, мұндағы
теңсіздігіне пара-пар, мұндағы
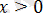 .
.
Жауабы:
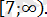
2. 1. 2-есеп.
Теңдеуді шешіңіз:
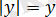 .
.
Шешуі:
Берілген теңдеуді
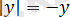 түрінде жазамыз. Бұл теңдеу
түрінде жазамыз. Бұл теңдеу
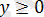 теңсіздігіне пара-пар, мұндағы
теңсіздігіне пара-пар, мұндағы
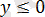 .
.
Жауабы:
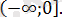
- түріндегі теңдеу
Бұндай теңдеулерді екі әдіспен шешуге болады.
Бірінші әдіс
-
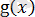 функциясы
функциясы
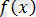 функциясына қарағанда қарапайымдылау болған жағдайда қолданылады.
функциясына қарағанда қарапайымдылау болған жағдайда қолданылады.
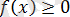 болғанда,
болғанда,
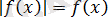 теңдігі орындалды және теңдеу
теңдігі орындалды және теңдеу
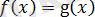 түріне енеді;
түріне енеді;
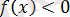 болғанда,
болғанда,
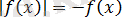 теңдігі орындалды және теңдеу
теңдігі орындалды және теңдеу
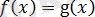 түріне енеді.
түріне енеді.
Керсінше, егер
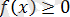 және
және
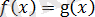 болса, онда
болса, онда
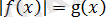 тең, ал егер
тең, ал егер
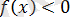 және
және
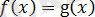 болса, онда тағы да
болса, онда тағы да
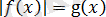 немесе
немесе
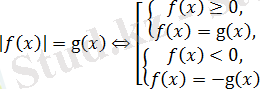
тең.
Сонымен қатар теңсіздікті шешудің қажеті жоқ, тек оған сәйкес теңдеуден алынған шешімді орынына қою керек. былай жасауға да болады:
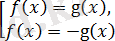 теңдеулер жиынтығын шешу керек, сосын жай ғана тексеруге болады.
теңдеулер жиынтығын шешу керек, сосын жай ғана тексеруге болады.
Берілген теңдеу
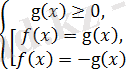
жүйесіне пара-пар деп айтуға болады.
2. 2. 1-есеп.
Теңдеуді шешіңіз:
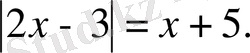
Шешуі:
Теңдеу келесідей жүйелер жиынтығына пара-пар:
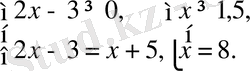
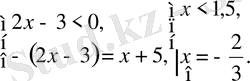
Жауабы:
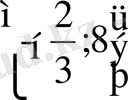
2. 2. 2-есеп.
Теңдеуді шешіңіз:
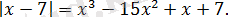
Шешуі:
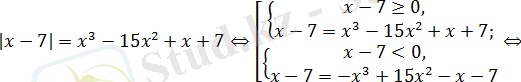

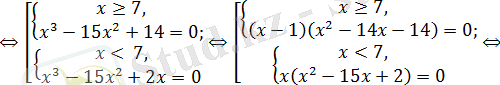
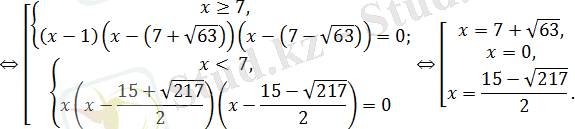
Жауабы:
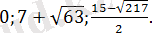
Екінші әдіс
-
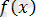 функциясы
функциясы
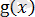 функциясына қарағанда қарапайымдылау болған жағдайда қолданылады.
функциясына қарағанда қарапайымдылау болған жағдайда қолданылады.
Егер
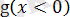 болса, онда
болса, онда
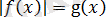 теңдеуінің шешімі болмайтынын көреміз. Егер де
теңдеуінің шешімі болмайтынын көреміз. Егер де
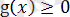 болса, онда
болса, онда
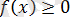 болғанда, теңдеу
болғанда, теңдеу
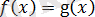 түріне енеді, ал
түріне енеді, ал
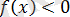 болғанда, теңдеу
болғанда, теңдеу
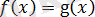 түріне енеді. Осыдан шығатыны
түріне енеді. Осыдан шығатыны
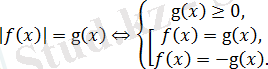
2. 2. 3-есеп.
Теңдеуді шешіңіз:

Шешуі:
Бұл мысалды екінші әдіспен шешкен тиімді, себебі түбірлер үшін
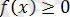 шартына қарағанда
шартына қарағанда
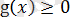 шартын тексерген әлде қайда жеңілірек.
шартын тексерген әлде қайда жеңілірек.
Сондықтан, егер
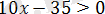 болса, онда
болса, онда
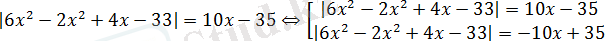
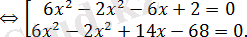
Бірінші теңдеудің сол жақ бөлігі топтастырылған көбейткіштер оңай жіктеледі, ал екінші теңдеуде
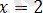 түбірі іздестіріледі және пара-пар жиынтық шығады
түбірі іздестіріледі және пара-пар жиынтық шығады
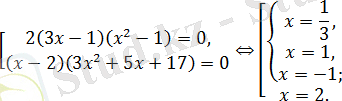
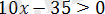 болатыны ескеріліп, жауапты аламыз.
болатыны ескеріліп, жауапты аламыз.
Жауабы:Шешімі жоқ.
2. 2. 4-есеп.
Теңдеуді шешіңіз:
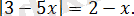
Шешуі:
Берілген теңдеу
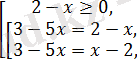 бұдан
бұдан
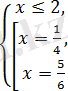
жүйесіне пара-пар.
 ,
,
 сандары
сандары
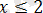 теңсіздігін қанағаттандырады және олар берілген теңдеудің түбірлері болады.
теңсіздігін қанағаттандырады және олар берілген теңдеудің түбірлері болады.
Жауабы:
 ,
,
 .
.
2. 2. 5-есеп.
Теңдеуді шешіңіз:
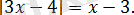
Шешуі:
Берілген теңдеу
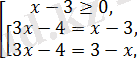 бұдан
бұдан
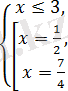
жүйесіне пара-пар.
 ,
,
 сандары
сандары
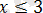 теңсіздігін қанағаттандырмайды және олар берілген теңдеудің түбірлері болмайды.
теңсіздігін қанағаттандырмайды және олар берілген теңдеудің түбірлері болмайды.
Жауабы:
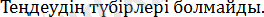
2. 2. 6-есеп.
Теңдеуді шешіңіз:
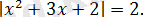
Шешуі :
Модульдің анықтамасына байланысты
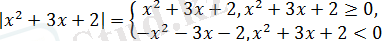
болады.
Теңсіздікті интервалдар әдісімен шешейік:
а)
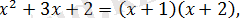 теңсіздіктің сол жақ бөлігі
теңсіздіктің сол жақ бөлігі
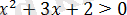 теріс емес, онда
теріс емес, онда
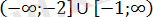 бірігу аралығындағы
бірігу аралығындағы
 -тің бұл мәні осы теңсіздіктің шешімі болады.
-тің бұл мәні осы теңсіздіктің шешімі болады.
б) теңсіздіктің сол жақ бөлігі
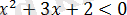
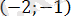 аралығында теріс.
аралығында теріс.
Берілген теңдеуді әр аралықта шешейік.
а)
 бұдан
бұдан
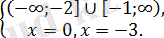
Алынған екі санда көрсетілген бірігу аралығына жатады және сондықтан олар алғашқы теңдеудің түбірі болады.
б)
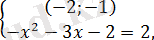
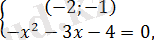
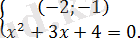
Жүйенің теңдеуінде нақты түбірлер болмайды, сондықтан
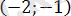 аралығында алғашқы теңдеудің түбірлері болмайды.
аралығында алғашқы теңдеудің түбірлері болмайды.
Жауабы:
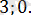
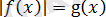 теңдеуін шешу үшін
теңдеуін шешу үшін
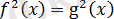 теңдеу- салдарына көшуге болады.
теңдеу- салдарына көшуге болады.
Бұны мысалмен көрсетейік (2. 2. 7-есеп) .
2. 2. 7-есеп.
Теңдеуді шешіңіз:
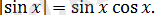
Шешуі:
Берілген теңдеудің екі жақ бөлігін квадраттасақ, алғашқы теңдеу салдары
болып табылатын
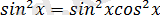 теңдеуін аламыз.
теңдеуін аламыз.
Теңдеудің барлық мүшелерін сол жағына көшіріп, ортақ көбейткішті жақша сыртына шығарамыз, негізгі тригонометриялық тепе-теңдікті қолдана отырып, соңғы теңдеуді
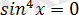 түрінде жазамыз. Бұл теңдеудің жалғыз ғана
түрінде жазамыз. Бұл теңдеудің жалғыз ғана
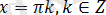 шешімдер топтамасы болады.
шешімдер топтамасы болады.
Тексеру көрсеткендей, осы барлық сандар берілген теңдеудің шешімдері болады.
Жауабы:
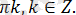
- түріндегі теңдеу.
Теңдеудің екі жақ бөлігі теріс болмағандықтан, онда
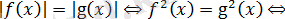
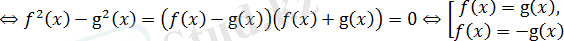
және біз пара-парлық шартын аламыз
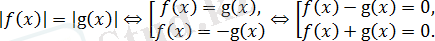
Оның ыңғайлылығы сол,
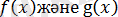 таңбаларымен ешқандай байланысы жоқ.
таңбаларымен ешқандай байланысы жоқ.
2. 3. 1-есеп.
Теңдеуді шешіңіз:
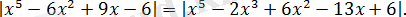
Шешуі:

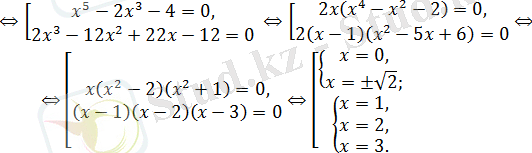
Біз мынандай жауап аламыз:
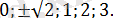
Жауабы:
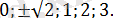
2. 3. 2-есеп.
Теңдеуді шешіңіз:
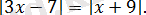
Шешуі:
Берілген теңдеу, теңдеулер жиынтығына пара-пар
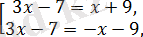 бұдан
бұдан
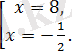
Жауабы:
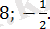
2. 3. 3-есеп.
Теңдеудің барлық түбірлері кіретін аралықты көрсетіңіз:
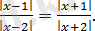
1)
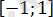 2)
2)
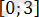 3)
3)
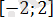 4)
4)
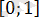
Шешуі:
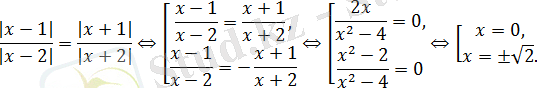
Бұл 3 түбірде
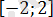 кесіндісінде жатады.
кесіндісінде жатады.
Жауабы: 3.
- түріндегі теңдеу.
Бұл теңдеу қос теңсіздікке пара-пар
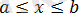 (ол туралы жоғарда айтылып кетті) .
(ол туралы жоғарда айтылып кетті) .
2. 4. 1-есеп.
Теңдеуді шешіңіз:
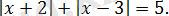
Шешуі:
Берілген теңдеуде
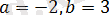 тең, онда
тең, онда
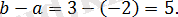 Берілген теңдеу
Берілген теңдеу
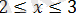 қос теңсіздігіне пара-пар.
қос теңсіздігіне пара-пар.
Жауабы:
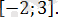
2. 4. 2-есеп.
Теңдеуді шешіңіз:
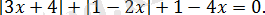
Шешуі:
Модуль ішіндегі өрнек
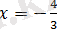 және
және
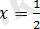 болғанда нөлге айналдырады. Теңдеудің анықталу облысы
болғанда нөлге айналдырады. Теңдеудің анықталу облысы
 ,
,
 сандары үш аралыққа бөлетін барлық сандар түзуі:
сандары үш аралыққа бөлетін барлық сандар түзуі:
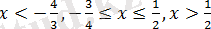 .
.
2. 4. 1-сурет
Берілген теңдеуді әр интервалда шешейік.
1)
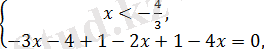 бұдан
бұдан
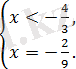
 саны
саны
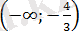 аралықта жатпайды, демек қаралып жатқан аралықта теңдеудің түбірі болмайды.
аралықта жатпайды, демек қаралып жатқан аралықта теңдеудің түбірі болмайды.
2)
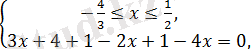 бұдан
бұдан
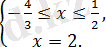
 саны
саны
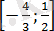 аралықта жатпайды, демек берілген теңдеудің де түбірі болмайды.
аралықта жатпайды, демек берілген теңдеудің де түбірі болмайды.
3)
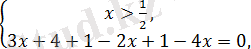 бұдан
бұдан
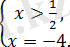
 саны
саны
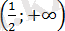 аралықта жатпайды, демек берілген теңдеудің түбірі болмайды.
аралықта жатпайды, демек берілген теңдеудің түбірі болмайды.
Жауабы: теңдеудің түбірі болмайды.
2. 4. 3-есеп.
Теңдеуді шешіңіз:
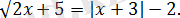
Шешуі:
Теңдеудің анықталу облысын табайық:
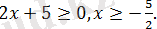
Онда
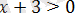 болады және сонымен қатар
болады және сонымен қатар
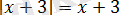 .
.
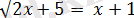 теңдеуін аламыз. Осыны шешетін болсақ, оған пара-пар теңдеу құрамыз:
теңдеуін аламыз. Осыны шешетін болсақ, оған пара-пар теңдеу құрамыз:
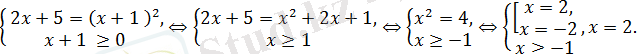
Жауабы:

2. 4. 4-есеп.
Теңдеуді шешіңіз:
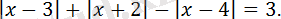
Шешуі:
 нүктелерінде модуль ішіндегі өрнек нөлге тең болады.
нүктелерінде модуль ішіндегі өрнек нөлге тең болады.
Берілген теңдеу
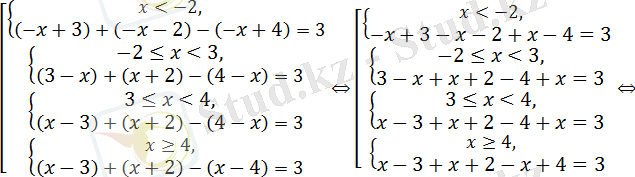
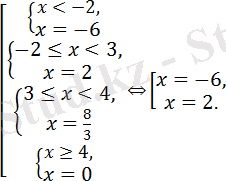
Жауабы:
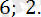
2. 4. 5-есеп.
Теңдеуді шешіңіз:
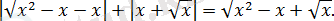
Шешуі:
Белгілеу енгізейік:
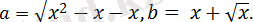
Онда алғашқы теңдеу
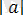 +
+
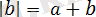 түріне енеді.
түріне енеді.
Модульдің қасиеті бойынша, бір уақытта

 және
және
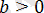 болғанда, сонда тек сонда ғана соңғы теңдік орындалуы мүмкін. Сондықтан алғашқы теңдеу
болғанда, сонда тек сонда ғана соңғы теңдік орындалуы мүмкін. Сондықтан алғашқы теңдеу
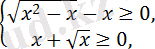 теңсіздіктер жүйесіне пара-пар, ол өз кезегінде
теңсіздіктер жүйесіне пара-пар, ол өз кезегінде
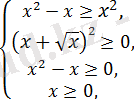 жүйесіне пара-пар, бұдан
жүйесіне пара-пар, бұдан
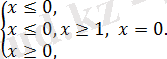
Жауабы: 0.
2. 4. 6-есеп.
Теңдеуді шешіңіз:
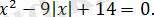
Шешуі:
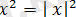 қасиеті бойынша берілген теңдеуін мынандай түрде жазуға болады:
қасиеті бойынша берілген теңдеуін мынандай түрде жазуға болады:
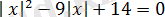 .
.
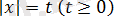 алмастыру енгізе отырып
алмастыру енгізе отырып
 теңдеуін аламыз. Виет теоремасы бойынша
теңдеуін аламыз. Виет теоремасы бойынша
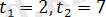
тең. Онда
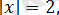 бұдан
бұдан
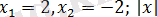 =7 бұдан
=7 бұдан
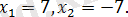
Жауабы:
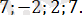
2. 4. 7-есеп.
Теңдеуді шешіңіз:
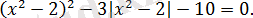 Жауабында барлық табылған түбірлердің қосындысын көрсетіңдер.
Жауабында барлық табылған түбірлердің қосындысын көрсетіңдер.
Шешуі:
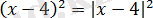 екенін ескере отырып,
екенін ескере отырып,
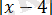 қатысты
қатысты
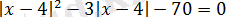 квадраттық теңдеуге келеміз.
квадраттық теңдеуге келеміз.
Алмастыру жасайық:
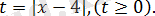
 теңдеуін аламыз. Бұны шешсек,
теңдеуін аламыз. Бұны шешсек,
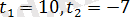 түбірлерін аламыз.
түбірлерін аламыз.
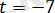 саны
саны
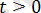 шартын қанағаттандырмайды. Мұндағы
шартын қанағаттандырмайды. Мұндағы
 болғанда,
болғанда,
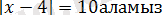 , бұдан
, бұдан
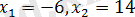 болады.
болады.
Түбірлерінің қосындысы
 -ге тең.
-ге тең.
Жауабы:
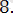
2. 4. 8-есеп.
Теңдеуді шешіңіз:
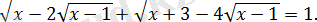
Шешуі:
Алғашқы теңдеуді
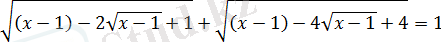
немесе
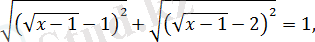
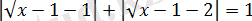

түрінде жазайық.
1 және 2 нүктелері сандық түзуді аралықтарға бөледі, әр аралықта модульді ашайық.
- Ондатеңдеуі
түріне енеді. Мұндағы
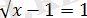
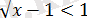 шартына қарама-қайшы. Сондықтан берілген теңдеудің қарастырылып отырған аралықта түбірлері болмайды.
шартына қарама-қайшы. Сондықтан берілген теңдеудің қарастырылып отырған аралықта түбірлері болмайды.
- Ондатеңдеуі
түріне енеді. Мұндағы
 Сондықтан теңдеудің
Сондықтан теңдеудің
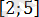 аралығында
аралығында
 -тің барлық мәндері дұрыс.
-тің барлық мәндері дұрыс.
- Ондатеңдеуі
немесе
түріне енеді. Бірақ соңғы теңдік
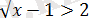 шартына қарама-қайшы, сондықтан алғашқы теңдеудің қарастырылып отырған аралықта түбірлері болмайды.
шартына қарама-қайшы, сондықтан алғашқы теңдеудің қарастырылып отырған аралықта түбірлері болмайды.
Жауабы:

2. 4. 9-есеп.
Теңдеуді шешіңіз:

Шешуі:
Модуль ішіндегі өрнек
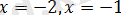 болғанда нөлге айналады. Осы нүктелермен сандық түзуді арлықтарға бөлеміз және берілген теңдеуді осы аралықтарда қарастырайық.
болғанда нөлге айналады. Осы нүктелермен сандық түзуді арлықтарға бөлеміз және берілген теңдеуді осы аралықтарда қарастырайық.
1)
 болсын. Аралас жүйені аламыз.
болсын. Аралас жүйені аламыз.
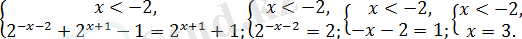
Сонымен
 аралығында алғашқы теңдеудің
аралығында алғашқы теңдеудің
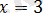 түбірі болады.
түбірі болады.
2)
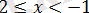 болсын. Онда бұл жағдайда
болсын. Онда бұл жағдайда
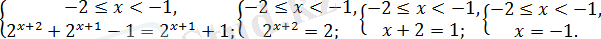
жүйесін аламыз.

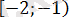 аралығында жатпайды. Сондықтан бұл аралықта алғашқы теңдеудің түбірі болмайды.
аралығында жатпайды. Сондықтан бұл аралықта алғашқы теңдеудің түбірі болмайды.
- болсын.
жүйесін аламыз.
Жүйедегі теңдеуден шығатыны,
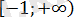 аралығында жататын
аралығында жататын
 кез келген сан, демек осы аралықта жататын
кез келген сан, демек осы аралықта жататын
 -тің барлық мәндері алғашқы теңдеудің түбірлері болады.
-тің барлық мәндері алғашқы теңдеудің түбірлері болады.
Жауабы:
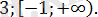
- «Күрделі» модульдерімен теңдеу.
«Күрделі» модуль деп, модуль ішінде функциясы бар, ж азылуында бір немесе бірнеше модулі болатын өрнекті атаймыз.
«Күрделі» модульдерімен теңдеуді интервалдар әдісімен шешуге болады.
2. 4. 10-есеп.
Теңдеуді шешіңіз:
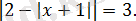
Шешуі:
Алғашқы теңдеу екі теңдеулер жиынтығына пара-пар
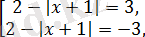 аламыз, бұдан
аламыз, бұдан
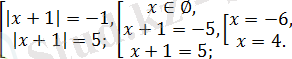
 бос жиынды білдіреді (теңдеудің түбірлері болмайды) .
бос жиынды білдіреді (теңдеудің түбірлері болмайды) .
Жауабы:
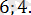
2. 4. 11-есеп.
Теңдеуді шешіңіз:
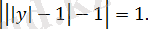
Шешуі:
Алғашқы теңдеудің екі теңдеулер жиынтығына пара-пар
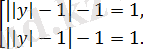 Жиынтықтың екінші теңдеуінен
Жиынтықтың екінші теңдеуінен
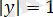 табамыз, онда
табамыз, онда
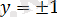 -ге тең. Жиынтықтың бірінші теңдеуінен
-ге тең. Жиынтықтың бірінші теңдеуінен
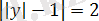
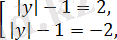 бұдан
бұдан
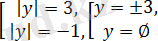 жиынтығына пара-пар.
жиынтығына пара-пар.
Алынған шешімдерді біріктіру арқылы жауабын табамыз.
Жауабы:
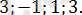
«Күрделі» модульмен теңдеуді біртіндеп модульдерді ашу арқылы («іш жағынан») шешкен жөн. Мысылдар қарастырайық.
2. 4. 12-есеп.
Теңдеуді шешіңіз:
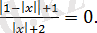
Шешуі:
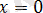 нүктесінде модуль ішіндегі өрнектің «ішкі»
нүктесінде модуль ішіндегі өрнектің «ішкі»
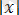 нөлге айналады.
нөлге айналады.
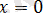 нүктесі сандық түзуді
нүктесі сандық түзуді
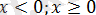 аралықтарға бөліп, берілген теңдеуді осы әр аралықта қарастырамыз.
аралықтарға бөліп, берілген теңдеуді осы әр аралықта қарастырамыз.
1)
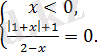
 нүктесімен (бұл модуль ішіндегі өрнектің түбірі)
нүктесімен (бұл модуль ішіндегі өрнектің түбірі)
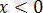 аралығын екі аралыққа бөлеміз:
аралығын екі аралыққа бөлеміз:
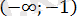 және
және
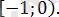
1а)
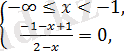 бұдан
бұдан
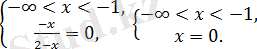
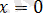 саны көрсетілген аралықта жатпайтындықтан, ол теңдеудің түбірі болмайды.
саны көрсетілген аралықта жатпайтындықтан, ол теңдеудің түбірі болмайды.
1б)
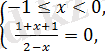 бұдан
бұдан
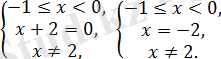
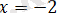 саны
саны
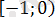 аралығында жатпайды, демек түбірі болмайды.
аралығында жатпайды, демек түбірі болмайды.
2)
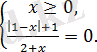
 нүктесімен
нүктесімен
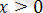 аралығын екі аралыққа бөлеміз:
аралығын екі аралыққа бөлеміз:
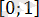 және
және
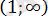 . Жүйедегі теңдеулерді осы әр аралықта қарастырамыз.
. Жүйедегі теңдеулерді осы әр аралықта қарастырамыз.
2а)
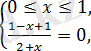 бұдан
бұдан
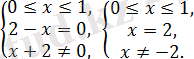
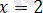 саны
саны
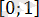 аралығында жатпайды, демек теңдеудің түбірі болмайды.
аралығында жатпайды, демек теңдеудің түбірі болмайды.
2б)
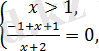 бұдан
бұдан
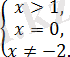
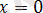 саны
саны
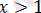 аралығында жатпайды және сондықтан теңдеудің түбірі болмайды.
аралығында жатпайды және сондықтан теңдеудің түбірі болмайды.
Жауабы: теңдеудің түбірі болмайды.
Функцияның жұптығының қасиетін қолдана отырып шығарылатын модульмен берілген теңдеулер болады. Мысалдар келтірейік.
2. 4. 13-есеп.
Теңдеуді шешіңіз:
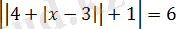 , жауабында түбірлерінің қосындысын көрсетіңіз.
, жауабында түбірлерінің қосындысын көрсетіңіз.
Шешуі:
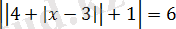
теңдеуі
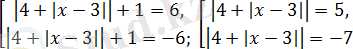
жиынтығына пара-пар.
Жиынтығының екінші теңдеуінің шешімі болмайды, ал бірінші теңдеуі жаңа жиынтыққа пара-пар
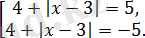
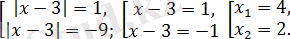
Түбірлерінің қосындысы
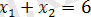 тең.
тең.
Жауабы:
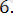
2. 4. 14-есеп.
Теңдеуді шешіңіз:
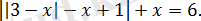
Шешуі:
Берілген теңдеуді
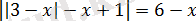 түрінде жазамыз. Соңғы теңдеу
түрінде жазамыз. Соңғы теңдеу
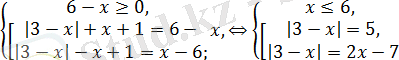
жиынтығына пара-пар.
Жиынтықтың бірінші теңдеуі
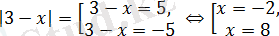
жиынтығына пара-пар.
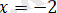 жүйенің шешімі болады.
жүйенің шешімі болады.
Екінші теңдеу келесі жүйеге пара-пар.
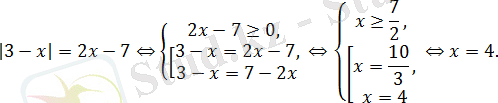
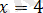 мәні де жүйенің шешімі болады.
мәні де жүйенің шешімі болады.
Жауабы:
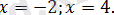
2. 4. 15-есеп.
Теңдеуді шешіңіз:
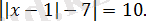
Шешуі:
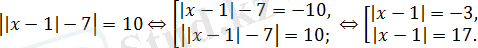
Жиынтықтың бірінші теңдеуінің шешімі болмайды. Жиынтықтың екінші теңдеуінің түбірлері
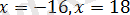 сандары болады.
сандары болады.
Жауабы:

2. 4. 16-есеп.
Теңдеуді шешіңіз:
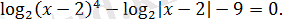
Шешуі:
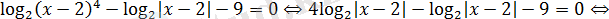
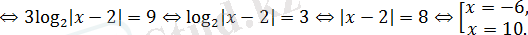
Жауабы:
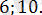
2. 4. 17-есеп.
Теңдеуді шешіңіз:
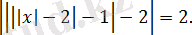
Шешуі:
Модульдің анықтамасы бойынша
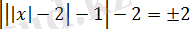 аламыз.
аламыз.
- теңдеуін шешеміз, бұдан
шығады. Онда
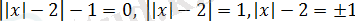 немесе
немесе
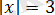 және
және
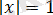 , бұдан
, бұдан
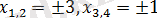 шығады.
шығады.
- теңдеуін шешеміз, бұдан
 немесе
немесе
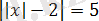 және
және
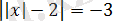 (соңғы теңдеудің шешімі болмайды) .
(соңғы теңдеудің шешімі болмайды) .
Сонымен,
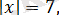 бұдан
бұдан
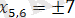 шығады.
шығады.
Жауабы:
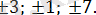
Модулі бар теңдеулерді шешуге көшейік.
2. 4. 18-есеп.
Теңдеуді шешіңіз:
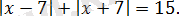
Шешуі:
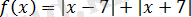 функциясы жұп, оның анықталу облысы нөлге қарағанда симметриялы болады және
функциясы жұп, оның анықталу облысы нөлге қарағанда симметриялы болады және

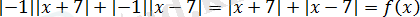 .
.
Теңдеудің түбірі
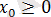 болсын. Онда функция жұп болғандықтан,
болсын. Онда функция жұп болғандықтан,
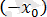 де теңдеудің түбірі болады.
де теңдеудің түбірі болады.
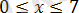 аралығында алғашқы теңдеу
аралығында алғашқы теңдеу
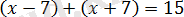 түріне енеді, бұдан
түріне енеді, бұдан
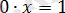 . Бұл теңдеудің түбірі болмайды.
. Бұл теңдеудің түбірі болмайды.
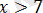 аралығында алғашқы теңдеу
аралығында алғашқы теңдеу
 түріне енеді, бұдан
түріне енеді, бұдан
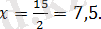
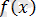 функциясының жұптылығына байланысты
функциясының жұптылығына байланысты
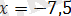 теңдеудің екінші түбірі болады.
теңдеудің екінші түбірі болады.
Уақытты үнемдеу үшін, үш аралықты қарастырудың орнына біз тек екі аралықты қарастырдық.
Жауабы:
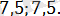
2. 4. 19-есеп.
Теңдеуді шешіңіз:
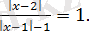
Шешуі:
Сандық түзуді
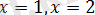 нүктелерімен
нүктелерімен
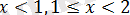 аралықтарына бөлейік (
аралықтарына бөлейік (
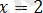 теңдеудің анықталу облысына кірмейді, себебі
теңдеудің анықталу облысына кірмейді, себебі
 тің бұл мәнінде бөлімі нөлге айналып кетеді) . Енді берілген теңдеуді әр аралықта қарастырайық.
тің бұл мәнінде бөлімі нөлге айналып кетеді) . Енді берілген теңдеуді әр аралықта қарастырайық.
- болсын. Онда
аламыз.
Көріп тұрғанымыздай,
 -тің ешқандай мәнінде
-тің ешқандай мәнінде
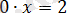 теңдігі орындалмайды.
теңдігі орындалмайды.
- болсын. Онда
аламыз, бұдан
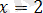 , бірақ
, бірақ
 -тің бұл мәні
-тің бұл мәні
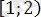 аралығына кірмейді, сондықтан алғашқы теңдеудің бұл аралықта түбірі болмайды.
аралығына кірмейді, сондықтан алғашқы теңдеудің бұл аралықта түбірі болмайды.
- болсын. Онда
аламыз, бұдан шығатыны,
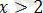 барлық мәндері
барлық мәндері
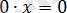 теңдеуінің түбірі болады, демек алғашқы теңдеудің де түбірі болады .
теңдеуінің түбірі болады, демек алғашқы теңдеудің де түбірі болады .
Жауабы:
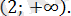
2. 4. 20-есеп.
Теңдеуді шешіңіз:
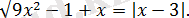
Шешуі:
Модуль ішіндегі өрнек
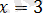 болғанда нөлге айналады, екі жағдайды қарастырайық.
болғанда нөлге айналады, екі жағдайды қарастырайық.
1)
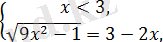 бұдан, жүйедегі теңдеудің екі жақ бөлігін квадраттағаннан кейін,
бұдан, жүйедегі теңдеудің екі жақ бөлігін квадраттағаннан кейін,
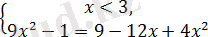
аламыз.
Жүйенің теңдеуін шеше келіп,
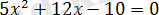 ,
,
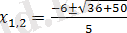 ,
,
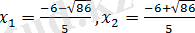 теңдеуіне келеміз.
теңдеуіне келеміз.
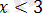 аралығына тек
аралығына тек
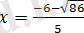 саны жатады.
саны жатады.
2)
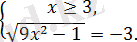
Теңдеудің сол жақ бөлігінде арифметикалық квадрат теріс емес түбір, ал оң жақ бөлігінде теріс сан тұрғандықтан жүйедегі теңдеулердің түбірлері болмайды.
Жауабы:
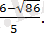
2. 4. 21-есеп.
Теңдеуді шешіңіз:
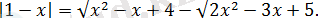
Шешуі:
 -тің кез келген нақты мәнінде түбір астындағы өрнек оң, демек берілген теңдеудің анықталу облысы
-тің кез келген нақты мәнінде түбір астындағы өрнек оң, демек берілген теңдеудің анықталу облысы
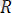 жиыны болады.
жиыны болады.
Теңдеудің екі жақ бөлігін
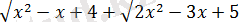
өрнегіне көбейтейік.
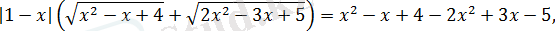
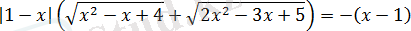
аламыз.
Берілген теңдеудің анықталу облысының барлық
 -да соңғы теңдеудің сол жақ бөлігі теріс емес, ал теңдеудің оң жақ бөлігі оң емес. Теңдеудің оң жақ және сол жақ бөлігі де нөлге тең болса, яғни
-да соңғы теңдеудің сол жақ бөлігі теріс емес, ал теңдеудің оң жақ бөлігі оң емес. Теңдеудің оң жақ және сол жақ бөлігі де нөлге тең болса, яғни
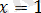 болған жағдайда ғана теңдік орындалады. Тексеру көрсеткендей
болған жағдайда ғана теңдік орындалады. Тексеру көрсеткендей
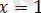 берілген теңдеудің түбірі болады.
берілген теңдеудің түбірі болады.
Жауабы:

2. 4. 22-есеп.
Теңдеуді шешіңіз:
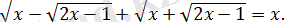
Шешуі:
Теңдеудің анықталу облысы жүйемен беріледі.
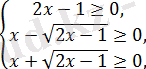 мұндағы
мұндағы
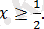
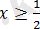 болғанда, берілген теңдеудің екі жақ бөлігін квадраттағаннан кейін, пара-пар теңдеу аламыз:
болғанда, берілген теңдеудің екі жақ бөлігін квадраттағаннан кейін, пара-пар теңдеу аламыз:
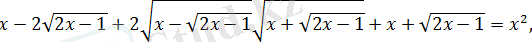
бұдан
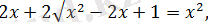
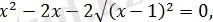
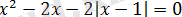

шығады.
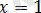 модуль ішіндегі өрнектің түбірі теңдеудің
модуль ішіндегі өрнектің түбірі теңдеудің
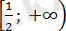 анықталу облысын екі аралыққа бөледі:
анықталу облысын екі аралыққа бөледі:
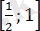 және
және
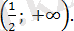
 теңдеуін әр аралықта қарастырайық.
теңдеуін әр аралықта қарастырайық.
- бұдан
шығады.
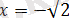 саны
саны
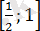 аралыққа жатпайды және түбірі болуы мүмкін емес.
аралыққа жатпайды және түбірі болуы мүмкін емес.
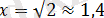 саны да бұл аралықта жатпайды. Демек
саны да бұл аралықта жатпайды. Демек
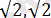 сандары бөгде түбірлер.
сандары бөгде түбірлер.
- бұдан
шығады.
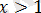 аралығына тек
аралығына тек
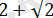 саны ғана жатады.
саны ғана жатады.
Жауабы:
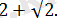
2. 4. 23-есеп.
Теңдеуді шешіңіз:
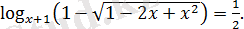
Шешуі:
Теңдеудің анықталу облысын жүйемен беріледі.
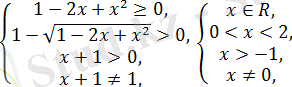 бұдан
бұдан
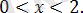
Берілген теңдеуді
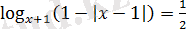 түрінде жазамыз.
түрінде жазамыз.
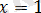 модуль ішіндегі өрнектің түбірі теңдеудің анықталу облысын екі аралыққа бөледі:
модуль ішіндегі өрнектің түбірі теңдеудің анықталу облысын екі аралыққа бөледі:
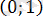 және
және
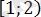 .
.
- бұдан
шығады.
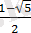 және
және
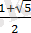 екі санда
екі санда
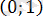 аралығында жатпайды, демек олар жүйенің теңдеудің түбірлері болмайды.
аралығында жатпайды, демек олар жүйенің теңдеудің түбірлері болмайды.
- бұдан
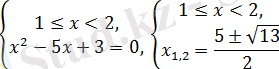
шығады.
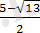 және
және
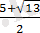 екі санда
екі санда
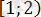 аралығында жатпайды, демек бөгде түбірлер болады.
аралығында жатпайды, демек бөгде түбірлер болады.
Жауабы: Теңдеудің түбірлері болмайды.
2. . 4. 24-есеп.
Теңдеуді шешіңіз:
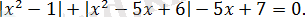
Шешуі:
Модульдің қосындысын ажыратайық:
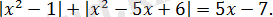
Сосын
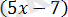 модуль ішіндегі өрнектің алгебралық қосындысы түрінде жазуға бола ма соны анықтауға тырысамыз.
модуль ішіндегі өрнектің алгебралық қосындысы түрінде жазуға бола ма соны анықтауға тырысамыз.
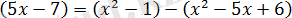
болғандықтан
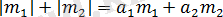
түріндегі теңдікті аламыз. Мұндағы
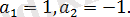 Сондықтан алғашқы теңдеу
Сондықтан алғашқы теңдеу
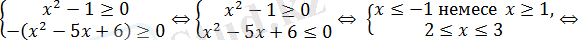

жүйесіне пара-пар.
Жауабы:
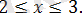
2. 4. 25-есеп.
Теңдеуді шешіңіз:
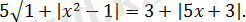
Шешуі:
Берілген есепті шешуді анықтама бойынша модульді ашудан бастаймыз, таңбаны анықтау үшін келесі кестені құрамыз. (2-кесте)
2-кесте
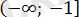
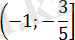
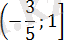
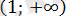



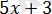
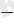


Берілген теңдеу төрт жүйенің жиынтығына пара-пар.
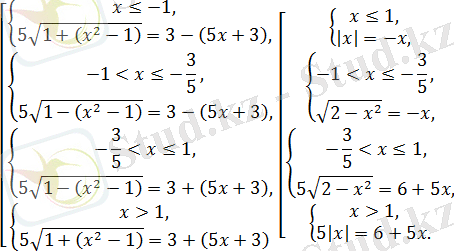
(Соңғы пара-парлық
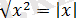 шығады) .
шығады) .
Бірінші жүйе жиынтығында
 аралықта шешімі болады, себебі осындай барлық
аралықта шешімі болады, себебі осындай барлық
 үшін
үшін
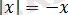 теңдігі дұрыс болатынын оңай көруге болады.
теңдігі дұрыс болатынын оңай көруге болады.
Екінші жүйеде көрсетілген барлық
 иррационалдық теңдеудің оң жақ бөлігі оң, сондықтан екі жағында квадраттауға болады:
иррационалдық теңдеудің оң жақ бөлігі оң, сондықтан екі жағында квадраттауға болады:
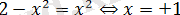 , демек екінші теңдеулер жүйсінің шешімі болмайды.
, демек екінші теңдеулер жүйсінің шешімі болмайды.
Үшінші жүйедегі көрсетілген барлық
 иррационалдық теңдеудің оң жақ бөлігі оң, сондықтан бұның да екі жағын да квадраттауға болады:
иррационалдық теңдеудің оң жақ бөлігі оң, сондықтан бұның да екі жағын да квадраттауға болады:

демек үшінші жүйедегі теңдеудің шешімі
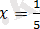 болады.
болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz