Оптика курсы бойынша электрондық оқулық: фотометрия, интерференция, дифракция және сәулелік оптика негіздері


МАЗМҰНЫ:
Кіріспе . . . 3
1. Фотометрия.
1. 1 Жарық шамалары . . . 4
1. 2. Жарық бірліктері . . . 6
1. 3. Жарық шамаларын өлшеу . . . 7
2. Интерференция.
2. 1. Интерференция құбылысы . . . 8
2. 2. Юнг тәжірибесі . . . 8
2. 3. Френель тәжірибесі . . . 9
2. 4. Жұқа пенка мен пластинкадағы интерференция . . . 10
2. 5. Ньютон сақиналары . . . 12
2. 6. Бірдей көлбеулік жолақтары . . . 13
2. 7. Интерферометрлер . . . 13
3. Жарық дифракциясы.
3. 1. Жарық толқынының дифракциясы . . . 14
3. 2. Гюйгенс-Френель принцпі . . . 14
4. Параллеь сәулелер дифракциясы.
4. 1. Фраунгофер дифракциясы . . . 17
4. 2. Оптикалық құралдардың ажырату
қабылеті . . . 18
4. 3. Рентген сәулелер дифракциясы. Вульф- Бреггер заңы . . . 19
4. 4. Оптикалық голография . . . 20
5. Жарық сәулесін спектрге жіктеу және спектрлік құралдардың
негізгі сипаттамасы .
5. 1. Призмалы спектрлік приборлар . . . 22
5. 2. Спектрдің түрлері . . . 24
5. 3. Спектрлік анализ . . . 24
6. Сәулелік оптика негіздері.
6. 1. Сәулелік оптика заңдары . . . 25
6. 2. Жарықтың жазық бетте шағылуы және сынуы . . . 26
6. 3. Толық ішкі шағылу құбылысы . . . 27
6. 4. Жарықтың сфералық бетте шағылуы мен сынуы . . . 28
6. 5. Жұқа линзалар . . . 30
6. 6. Жұқа линзадағы нәрсенің кескіні. Линзаның ұлғайтуы . . . 32
7. Оптикалық жүйелер. Оптикалық жүйелердің аберрациясы.
7. 1. Оптикалық жүйелер . . . 34
7. 2. Оптикалық жүйелердің аберрациясы . . . 35
7. 3. Жарық шоқтарын ықшамдау . . . 37
7. 4. Кескіннің жарықталынуы мен жарықтылығы . . . 38
7. 5. Көз-оптикалық жүйе. Көру . . . 39
7. 6. Визуаль оптикалық приборлар . . . 40
8. Жарықтың поляризациясы.
8. 1. Жарық сәулесінің қосарланып сынуы . . . 42
8. 2. Николь призмасы. Поляроид . . . 44
8. 3. Жарықтың эллипстік және дөңгелектік поляризациясы . . . 45
8. 6. Поляризацияланған жарық интерференциясы . . . 46
9. Жарық дисперсиясы, шашырауы және жұтылуы.
9. 1. Жарықтың дисперсиясы . . . 48
9. 2. Жарықтың шашырау . . . 49
9. 3. Жарықтың жұтылуы . . . 51
10. Жылулық сәуле шығару.
10. 1. Жылулық сәулелену. Кирхгоф заңы . . . 51
10. 2. Стефан-Больцман және Вин заңы . . . 54
10. 3. Рэлей-Джинс формуласы . . . 55
10. 4. Планк формуласы . . . 56
10. 5. Оптикалық пирометрия . . . 58
11. Люминесценция .
11. 1. Фотолюминесценция . . . 59
11. 2. Люминесценцияның қолдануы . . . 61
11. 3. Фотохимиялық реакциялар . . . 61
12. Жарықтың әсерлері.
12. 1. Фотоэлектрлік эффект . . . 63
12. 2. Эйнштейн теңдеуі. Жарық кванты . . . 65
12. 3. Фотоэлектр құбылысын пайдалану . . . 66
13. Фотонның массасы мен импульсі.
13. 1. Жарық қысымы . . . 67
13. 2. Фотонның массасы мен импульсі . . . 68
13. 3. Комптон эффектісі . . . 70
14. Жарық жылдамдығы.
14. 1. Жарықтың жылдамдығы . . . 72
14. 2. Жарықтың фазалық және топтық жылдамдығы . . . 76
14. 3. Доплер құбылысы . . . 77
15. Бейсызық оптика.
15. 1. Оптикалық кванттық генераторлар . . . 78
15. 2. Вавилов-Черенков сәулеленуі . . . 81
Қорытынды . . . 82
Қолданылған әдебиеттер . . . 83
КІРІСПЕ
Ғылым мен техниканың қарыштап дамуы, басқа да салалар сияқты білім беру саласын да заман талабына сай құру қажет болды. Қазіргі кезде компьютер мен басқа да ақпараттық технология білім беру саласында кеңінен қолданыла бастағаны белгілі. Компьютерлік техника және Интернет желісінің жақсы жетілуі қашықтан оқуыту жүйесін дамытуға мүмкіндік туғызып отыр. Осы мүмкіндікті іске асыруда білім беру құралдарының құрамдас бөлігі ретінде электрондық оқулықтар пайдаланыла бастады.
Дәстүрлі оқыту түріне қарағанда қашықтан оқытудың бірнеше артықшылықтары бар. Дәстүрлі оқыту жүйесінің кемшілігі сол, білім алушы көп уақытын босқа өткізеді және тек оқытушының қадағалауымен ғана оқиды. Ал қашықтан оқыту жүйесінде білім алушы кез келген уақытта өз бетімен білім алуына жағдай туады. Бұл - білім алушының еркін ойлауына, өз бетімен жұмыс істеуіне туған мүмкіндік деген сөз. Сөйтіп біз қашықтан оқыта отырып, еркін ойлай алатын, өз бетімен жұмыс істейтін жеке тұлға қалыптастырамыз.
Қашықтан оқыту жүйесінде оқытушы ақпарат беруші емес, кеңесші, бағыт-бағдар беруші рөлінде болады.
Жоғарыда айтқандай, несиелік жүйеде электрондық оқулықтар оқыту құралдарының негізгісі болып табылады. Оның үстіне қазіргі кезде тиісті әдебиеттер де жетіспейді. Осыдан барып электрондық оқулықтар құру қажеттілігі туып отыр. Ал қазақ тіліндегі электрондық оқулықтар мүлде аз. Бұл мәселе мемлекет деңгейінде қарастырылып отыр.
Сондықтан бұл дипломдық жұмыс - оқытудың несиелік жүйесінің шарттарын ескере отырып жасалған оптика курсы бойынша құрылған электрондық оқулық.
Оптика курсы бойынша электрондық оқулық құрамына модульдерге бөлінген оптика курсының теориясы және электрондық оқулыққа енгізілген материалдар толығымен Қазақстан Республикасы мемлекеттік стандарттарына сәйкес келеді.
І модуль
1. Фотометрия
1. 1. Жарық шамалары
1. Жарық энергиясы. Жарық ағыны. Жарық толқындары тасымалдайтын энергия жарық энергиясы немесе сәулелік энергия (W) деп аталады. Егер Жарық таралған кеңістікте кішкене ауданша бар болса, одан үздіксіз сәулелік энергия ағып өтіп жатады. Берілген ауданнан уақыт бірлігі ішінде өтетін сондай энергия мөлшері сәулелік энергия ағыны (Фэ) деп аталады; оны қуат өлшеу бірлігімен, мысалы, Вт-пен өлшеуге болады.
Сәулелік энергия ағынының көзге әсер етіп, көру сезімін туғызатын бөлігі ж а р ы қ а ғ ы н ы
(Ф)
деп аталады. Электромагниттік толқындардың бәрі бірдей көру сезімін оята бермейді, тек толқын ұзындықтары, шамамен, 0, 4
мкм-яея
0, 76
мкм-ге
не-месе 400
нм
ден 76, 0
нм-ге
дейінгі түсті сәулелер ғана көру сезімін туғызады. Оның өзінде де адамның көзінің түрліше түсті сәулелерді сезу дәрежесі бірдей емес. Көз толқынының ұзындығы 555
нм-ге
тең жасыл сәулені өте сезгіш-ақ, оған жайсарлас қысқа және ұзын толқынды түсті сәулелерді кез одан гөрі нашарлау сезеді. Ультракүлгін және инфрақызыл сәулелер, тіпті, көрерлік сезім туғызбайды, оларды көз көрмейді. Сөйтіп көздің түрлі түсті сәулелерді сезгіштігі сәуленің толқын ұзындығына тәуелді. Сонымен қабат әр адамның кезінің бір түсті сәулені сезгіштігі әр түрлі болады. Сондықтан практикада кездің «о р т а ш а» жарық сезгіштігі деген ұғым пайдаланылады. Орташа сезгіштік кезінің ақауы жоқ көптеген кісілердің көруін зерттеу арқылы тағайындалады. Адам көзінің толқынының ұзындықтары әр түрлі жарық сәулелерін «орташа» салыстырма сезгіштігін сипаттайтын шама көріну
функциясы
(
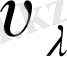 ) деп аталады. Бұл функцияның сан мәні түсті түрліше сәулелер үшін әр түрлі болады. Адамның көзі ете жақсы сезетін толқын ұзындығы 555
нм-ге
тең жасыл сәулеге тән көріну функциясы
) деп аталады. Бұл функцияның сан мәні түсті түрліше сәулелер үшін әр түрлі болады. Адамның көзі ете жақсы сезетін толқын ұзындығы 555
нм-ге
тең жасыл сәулеге тән көріну функциясы
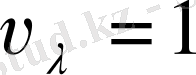 деп саналады, сонда басқа түсті сәулелерге тән
деп саналады, сонда басқа түсті сәулелерге тән
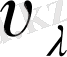 мәндері бірден кем (
мәндері бірден кем (
 ) болады. Көрінетін жарықтан тыс жатқан сәулелерге тән
) болады. Көрінетін жарықтан тыс жатқан сәулелерге тән
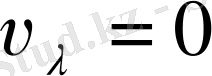 болады. Жарық ағыны көріну функциясы мен сәулелік энергия ағынының кьбейтіндісіне тең болады. Егер
болады. Жарық ағыны көріну функциясы мен сәулелік энергия ағынының кьбейтіндісіне тең болады. Егер
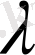 -ға таяу енділігі
-ға таяу енділігі
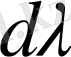 спектр участогына келетін сәулелік энергия ағыны
спектр участогына келетін сәулелік энергия ағыны
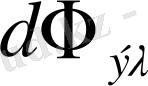 болса, спектрдін сол участогына тән жарық ағыны
болса, спектрдін сол участогына тән жарық ағыны
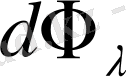 былай өрнектеледі:
былай өрнектеледі:
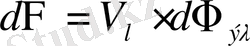 (1. 1)
(1. 1)
Сонда керінетін спектрге келетін толық жарық ағыны мынаған тең:
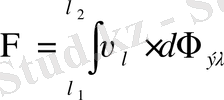 (1. 2)
(1. 2)
мұндағы
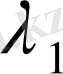 мен
мен
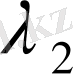 -спектрдің екі шетіне тән жарық толқыны ұзындықтары.
-спектрдің екі шетіне тән жарық толқыны ұзындықтары.
2. Жарық күші.
Егер нүктелік жарық көзінен шыққан көрінетін жарық барлық жаққа бір қалыпты таралып, толық денелік бұрыш (
 стерадиан) қамтитын барлық жарық ағыны
Ф
болса, онда бір
стерадианға тең денелік бұрышқа келетін жарық ағыны,
яғни
жарық күші (I)
мынаған тең болады:
стерадиан) қамтитын барлық жарық ағыны
Ф
болса, онда бір
стерадианға тең денелік бұрышқа келетін жарық ағыны,
яғни
жарық күші (I)
мынаған тең болады:
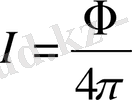 (1. 3)
(1. 3)
Практикада кездесетін жарық көздерінен шығатын жарық ағыны барлық жаққа бір қалыпты таралмайды. Сондықтан мұндай жағдайларда (3) өрнек тек орташа жарық күшін көрсетеді де
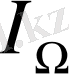 орташа сфералық жарық күші
деп аталады. Берілген бір бағыттағы шын жарық күшін табу үшін осы бағыт бойынша элементар денелік бұрыш
(
орташа сфералық жарық күші
деп аталады. Берілген бір бағыттағы шын жарық күшін табу үшін осы бағыт бойынша элементар денелік бұрыш
(
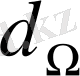 )
алынып, сол денелік бұрышқа келетін
)
алынып, сол денелік бұрышқа келетін
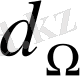 жарық ағыны өлшенеді. Сонда осы бағыттағы жарық күші
жарық ағыны өлшенеді. Сонда осы бағыттағы жарық күші
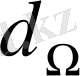 былай өрнектеледі:
былай өрнектеледі:
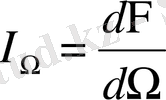 (1. 4)
(1. 4)
Егер жарық ағыны барлық жаққа бір қалыпты таралатын болса, жарық көзінен шығатын толық жарық ағыны (1. 3) формула бойыншамынаған тең болады:
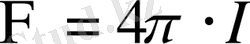 (1. 5)
(1. 5)
3. Жарықталыну. Өздері жарық шығармайтын денелер оларға жарық түссе ғана көрінеді, өйткені ондай денелерге түскен жарық азды-көпті шағылып жан-жағына шашырайды, дене дербес жарық көзі тәрізді болады. Дене неғұрлым күштірек жарықталса, соғұрлым одан жарық көп шашырайды. Дененің жарық болу дәрежесін сипаттау үшін жарықталыну деген шама пайдаланылады. Сонда жарықталыну (Е) деп жарық түскен dS беттің аудан өлшеу бірлігіне келетін жарық ағыны айтылады, яғни,
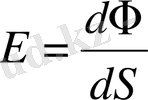 (1. 6)
(1. 6)
Мұндағы
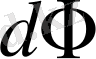 -
дененің бетіне түскен жарық ағыны.
-
дененің бетіне түскен жарық ағыны.
Мысалы, жарық түскен беттің
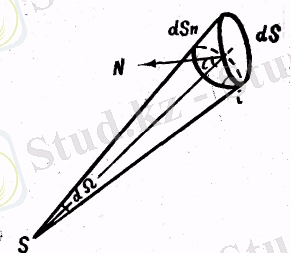
нүктедей жарық көзінен (1-сурет) қашықтығы r болып, сол бетке жүргізілетін нормаль мен түскен сәулелер аралығындағы бұрыш
і
болсын. Жарық көзі тұрған орыннан қарағанда
dS
көрінер денелік бұрыш
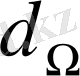 болсын, сонда бұл бетке
болсын, сонда бұл бетке
түсетін жарық ағыны
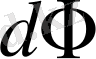 мынаған тең болады:
мынаған тең болады:
Мұндағы I - жарық күші. Денелік бұрыш мынаған тең:
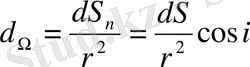
Олай болса жарық ағыны мынаған тең болады:
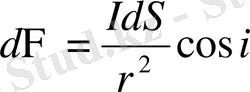
Жарық ағынының осы мәнін (1. 6) теңдіктегі орынына қойсақ, мынау шығады:
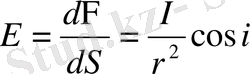 (1. 7)
(1. 7)
Сөйтіп, беттің жарықталынуы жарық күшіне, түсу бұрышы косинусына тура пропорционал, жарық көзі мен беттің ара қашықтығының квадратына кері пропорционал. Жарықталудың бұл заңы тек жарық көзінің өлшемдері жарық түскен бет ара қашықтығымен салыстырғанда өте кішкене, яғни жарық көзі нүктедей болса ғана дұрыс орындалады.
 4.
Жарқырау.
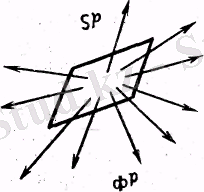
Практикада кездесетін жарық көздері аумақты болады, мысалы жарқырауық қатты дененің белгілі өлшемдері болады. Осындай жарық көзінің
4.
Жарқырау.
Практикада кездесетін жарық көздері аумақты болады, мысалы жарқырауық қатты дененің белгілі өлшемдері болады. Осындай жарық көзінің
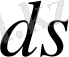 бетінің (2-сурет) бір жағына, яғни
бетінің (2-сурет) бір жағына, яғни
 -ға тең денелік бұрыш ішінде таралған жарық ағынының сол
-ға тең денелік бұрыш ішінде таралған жарық ағынының сол
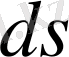 бетке қатынасы, яғни
жарық көзі
бетке қатынасы, яғни
жарық көзі
бетінің әрбір аудан бірлігінен шығатын жарық ағыны, жарқырау (R) деп аталады, сөйтіп,
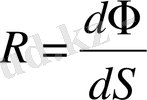 (1. 7)
(1. 7)
мұндағы
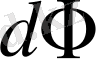 - жарық ағыны.
- жарық ағыны.
Жарқырау мен жарықталыну өрнектері бір-біріне ұқсас. Бірақ жарқырау өрнегінде
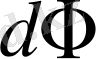 қарастырылып отырған жарқырауық беттен шығатын жарық ағынын, ал жарықталыну өрнегінде болса
қарастырылып отырған жарқырауық беттен шығатын жарық ағынын, ал жарықталыну өрнегінде болса
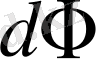 алынған бетке сырттан түсетін жарық ағынын көрсетеді.
алынған бетке сырттан түсетін жарық ағынын көрсетеді.
Дербес жарық көзі емес денелердің (мысалы, жарық шашыратқыш беттердің) жарқырауы оның жарықталынуына тура пропорционал, яғни
 (1. 9)
(1. 9)
мұндағы к - шашырау коэффициенті делінетін шама, нақты денелерге тән к мәні бірден кем (к< 1) болады.
5. Жарықтылық.
Белгілі өлшемдері бар жарық көзінің жарық шығаруын сипаттау үшін жарықтылық делінетін шаМа дэ қолданылады.
Жарық көзінің жарықтылығы (В) деп жарық көзінен берілген бағытта кішкене
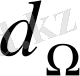 денелік бурыш ішінде таралған жарық ағынының сол бұрышқа және жарық көзінің көрінер бетіне қатынасы айтылады.
Жарық мысалы, алынған бетке жүргізілген нормальмен
денелік бурыш ішінде таралған жарық ағынының сол бұрышқа және жарық көзінің көрінер бетіне қатынасы айтылады.
Жарық мысалы, алынған бетке жүргізілген нормальмен
 -бұрышы жасалатын бағытта таралған болса, онда жарықтылық мынаған тең болады:
-бұрышы жасалатын бағытта таралған болса, онда жарықтылық мынаған тең болады:
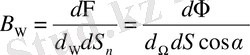 (1. 10)
(1. 10)
мұндағы
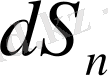 -жарқырауық беттің сәулеге перпендикуляр жазықтыққа түсірілген проекциясы,
-жарқырауық беттің сәулеге перпендикуляр жазықтыққа түсірілген проекциясы,
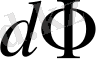 -жарық ағыны.
-жарық ағыны.
Жарықтылық пен жарық күші бірімен бірі байланысты. Расында (1. 10) өрнекке енген
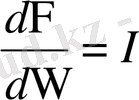 ,
ендеше ол өрнекті былай жазуға да болады:
,
ендеше ол өрнекті былай жазуға да болады:
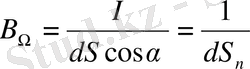 (1. 11)
(1. 11)
Сөйтіп, жарықтылық шамасы жарық көзі бетінің бірлігінен нормаль бағыты бойынша шығатын жарық күшіне тең.
Егер жарықтылық шамасы жарық таралатын бағытқа тәуелді болмаса, онда жарқырауық ауданнан элементар
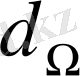 денелік бұрыш ішінде таралатьш жарық ағыны
денелік бұрыш ішінде таралатьш жарық ағыны
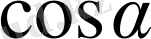 -ға пропорционал олады, яғни (1. 10) теңдік бойынша:
-ға пропорционал олады, яғни (1. 10) теңдік бойынша:
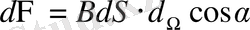 (1. 12)
(1. 12)
Осы шарт орындалатын жарқырауық денелер
косинустік жарық өздері деп аталады. Осындай жарық көздерінің жарықтылығы тұрақты болады.
Белгілі өлшмедері бар косинустік жарық көздерінің жарқырауы (R) мен жарықтылығы (В) өзара байланысты, атап айтанда:
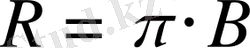 (1. 13)
(1. 13)
ғни
жарқырау шамасы жарықтылықтан
 = 3, 14
есе артық.
= 3, 14
есе артық.
1. 2. Жарық бірліктері
1)
Жарық күшінің бірлігі - Кандела
(қысқаша
кд) .
Өлшеуіштер мен таразылар жайындағы XIII Бас конференцияның ұйғаруы бойынша:
«Қандела дегеніміз платинаның қату темперарасында толық сэуле шығарғыштыц жарыщтылығы оның әрбір шдрат сантиметр бетіне 60 канделадан келген жағдайдағы жарық күші»
.
Басқаша айтқанда, кандела дегеніміз платинаның қату температурасында, 2046, 6°
К-
да
,
абсолют қара дененің 1 квадрат сантиметр бетінің оған жүргізілген нормаль бағыты бойынша шығаратын жарық күшінің
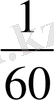 үлесі болады.
үлесі болады.
2 ) Жарық ағынының бірлігі - люмен (қысқаша лм) . Люмен дегеніміз жарық күщі 1 кд-ға тең жарық көзінен шығып 1стерадианға тең денелік бұрыш ішінде таралатын жарық ағыны. Сонда (1. 4) формула бойынша:
1 лм = 1 кд • 1 стер.
3) Жарықталыну бірлігі - люкс (қысқаша лк ) . Люкс дегенміз 1 квадрат метр бетке 1 люмен жарық ағыны келген беттің жарықталынуы. (1. 6) формула бойынша:
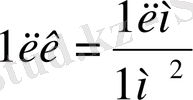
5) Жарықтылық бірлігі ретінде 1 квадрат метр ауданы нормаль бағыт бойынша күші 1 кд-ға тең жарық беретін беттің жарықтылығы алынады; ол (1. 11) формула бойынша мынаған тең:
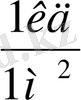 .
.
Жарықтылық стильб (қысқаша сб) деп аталатын бірлікпен де өлшенеді.
Жарық ағынының орнына сәулелік энергия ағыны деген ұғымды пайдаланып, осы айтылған жарық шамаларына сәйкес энергетикалық жарық күші (
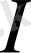 э
), энергетикалық жарықталыну
(Е
э
),
энергетикалық жарқырау (
э
), энергетикалық жарықталыну
(Е
э
),
энергетикалық жарқырау (
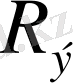 ), энергетикалық жарықтылық
(В
э
)
деп аталатын шамалар да қолданылады. Бұлар механикалық бірліктермен өлшенеді. Мысалы, сәулелік энергия ағыны Вт-пен, энергетикалық жарық күші
), энергетикалық жарықтылық
(В
э
)
деп аталатын шамалар да қолданылады. Бұлар механикалық бірліктермен өлшенеді. Мысалы, сәулелік энергия ағыны Вт-пен, энергетикалық жарық күші
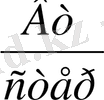 пен, энергетикалық жарықталыну
пен, энергетикалық жарықталыну
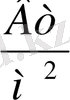 -пен өлшенеді.
-пен өлшенеді.
1. 3. Жарық шамаларын өлшеу
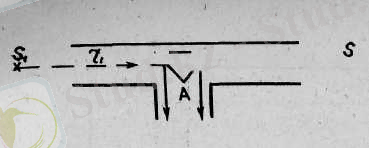 Жарық энергиясын, оған байланысты шамаларды өлшеу методтары мен тәсілдері қарастырылатын оптика тарауы
фотометрия
деп аталады. Жарық шамаларын тікелей көзбен бақылап (визуальдық методтар колданып) немесе басқа жарық қабылдағыштарды пайдаланып (объективтік методтар қолданып) өлшеуге болады. Жарық шамаларын өлшеуге арналған приборлар фотометрлер деп аталады. Олар қолданылатын методтарға сәйкес визуальдық және объективтік фотометрлер деп екі түрге бөлінеді.
Жарық энергиясын, оған байланысты шамаларды өлшеу методтары мен тәсілдері қарастырылатын оптика тарауы
фотометрия
деп аталады. Жарық шамаларын тікелей көзбен бақылап (визуальдық методтар колданып) немесе басқа жарық қабылдағыштарды пайдаланып (объективтік методтар қолданып) өлшеуге болады. Жарық шамаларын өлшеуге арналған приборлар фотометрлер деп аталады. Олар қолданылатын методтарға сәйкес визуальдық және объективтік фотометрлер деп екі түрге бөлінеді.
Визуальдық методтар жапсарлас екі беттің жарықтылығын, демек олардың жарықталынуын көзбен бақылап салыстыруға негізделеді, адамның көзі бір түсті жарық түскен ондай екі беттің жарықтылығы тең екендігін өте дәл айыра алады. Бірқатар фотометрлердің қызмет істеуі осы принципке негізделген.
Үш жақты призмалы фотометр (3-сурет) осындай фотометрдің қарапайым түрі болады. Іші қарайтылран трубаның ішіне орнатылған үш жақты АВС призмасьшьщ екі жағына (бір түзу бойына) жарық күштері салыстырылатып S 1 және S 2 жарық көздері қойылады. Бүлар ABC призмадан едәуір алыс және өздері кішкене болса, онда (1. 7) формула бойынша АВ және АС жақтарының жарықталынуы мынаған тең болады:
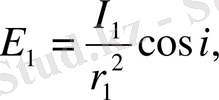
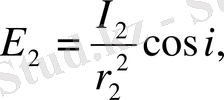 (1. 14)
(1. 14)
мұндағы
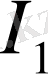 мен
мен
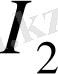 - алынған жарық көздерінің күштері,
- алынған жарық көздерінің күштері,
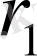 мен
мен
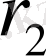 -олардың призмадан қашықтықтары;
і
- жарықтың түсу бұрышы. Жарық көздерінід біреуін қозғап, призмадан алыстата, не жақындата отырып, оның көршілес екі жағының жарықталынуын теңгеруге болады, сонда
Е
1
= Е
2
болады да (1. 14) өрнектерден мынаны табамыз:
-олардың призмадан қашықтықтары;
і
- жарықтың түсу бұрышы. Жарық көздерінід біреуін қозғап, призмадан алыстата, не жақындата отырып, оның көршілес екі жағының жарықталынуын теңгеруге болады, сонда
Е
1
= Е
2
болады да (1. 14) өрнектерден мынаны табамыз:
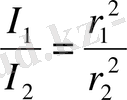 (1. 15)
(1. 15)
 Сөйтіп,
Сөйтіп,
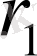 мен
мен
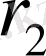 аралықтарын өлшеп тауып, екі жарық көзі күштерінің қатынасын (
аралықтарын өлшеп тауып, екі жарық көзі күштерінің қатынасын (
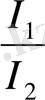 ) табуға болады. Егер олардың біреуінің жарық күші мәлім болса, екеншісінің жарық күшін есептеп таба аламыз.
) табуға болады. Егер олардың біреуінің жарық күші мәлім болса, екеншісінің жарық күшін есептеп таба аламыз.
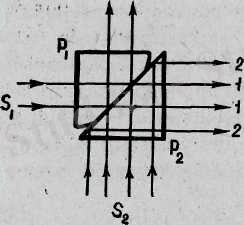
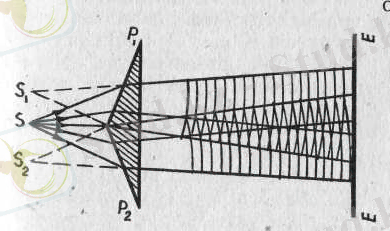
Люммер-Бродхун фотометрі. Бүл фотометрдің негізгі бөлімі Люммер кубшесі (4, а-сурет) болады. Ол күбше тік бұрышты Р 1 және Р 2 деп белгілеген екі шыны призмадан жасалады. Олардың біреуінің (Р 1 - призманың) гипотенузасына сәйкес жағының шеті жұмырлап жонылған, орта жері жазық, болады. Призмалар гипотенузалары бойымен бір-біріне жабыстырылып қойылған, сол жақтағы S 1 жарық көзінен (4, б-сурет) келген жарық шоғы Е 1 және Е 2 ақ экрандардан шағылған соң
кубшеге түседі, оның екі призманың тиісіп түрған орнына түскен үлесі сынбай өтеді (суретте «1» деп белгіленген),
Р
1
призманың жонылған жерлеріне түскен үлесі басқа жаққа шашырап кeтеді. S
2
жарық көзінен келген жарық шоғы да
Е
және
Е
2
экрандардан шағылған соң кубшеге түседі; оның призмалардың тиісіп тұрған жеріне түскен үлесі сынбай өтіп кетеді.
Р
2
призма бетінің түйіспей тұрған жерлеріне түскен жарық шоғы іштен толық шағылады да бірінші жарық шоғы таралған жаққа қарай таралады (суретте «2» деп белгіленген) . Сөйтіп кубшенің бір жағына қарай екі жарық көзінен келген жарық шоқтары таралады. Бүлардың екеуі де көру трубасына енеді де 1-шоқ түскен жарық дөңгелек дақ. оны қоршаған сақина тәрізді 2-шоқ түскен белдеуше дақ көрінеді. Егер бұлардың жарықталынуы тең болмаса, олардың шекаралары айқын көрініп тұрады, ең болса - жапсары білінбейді. Өлшеу жүргізілгенде S
1
және S
2
жарық көздерін жылжыта отырып осы дақтардың жарықталынуы теңгеріледі,
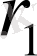 мен
мен
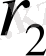 ара қашықтықтары өлшенеді. (1. 7) формула бойынша алынған жарық көздерінің жарық күштерінің қатынасы
ара қашықтықтары өлшенеді. (1. 7) формула бойынша алынған жарық көздерінің жарық күштерінің қатынасы
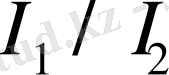 табылады. Егер бүлардың біреуінің жарық күші мәлім болса, екіншісінің жарық күшін анықтауға да болады.
табылады. Егер бүлардың біреуінің жарық күші мәлім болса, екіншісінің жарық күшін анықтауға да болады.
2- модуль
Интерференция
2. 1. Интерференция құбылысы
Жарықтың толқындық табиғаты интерференция құбылысынан айқын көрінеді. Бұл құбылысты табиғи жағдайда да жиі байқауға болады. Мысалы, суға тамған май мұнай кілегейлеріне, сабын көпіршігіне және слюданың қабыршағына күн сәулесі түскенде олардың беттері қызыл-жасыл болып құбылып тұрады. Мұнда жолақтардың түрлі -түсті болуы көпіршік пен сұйыққа ақ жарық түскендіктен болады. Егер сабын көпіршігіне түсетін ақ жарық жолына, мысалы, жасыл шыны қойылса, онда көпіршіктің бетінде тек аралықтары қара қоңыр жасыл жолақтар байқалады. Басқаша айтқанда жұқа пленка бетіне бір түсті (монохроматты) жарық түсірілсе, сонда аралары қара қоңыр жолақпен бөлінген бір түсті жолақтар байқалады, бірақ олардың жарықталынуы бірдей болмайды. осындай жарық және қара қоңыр жолақтардың пайда болуы -жұқа пленка беттерінен шағылған жарық толқындары бірімен бірі қосылысқанда, олардың бірін-бірі күшейту немесе әлсірету себебінен болады. Бұл құбылыс жарықтың интерференциясы деп аталады. Интерференция тек жарық толқындарында ғана емес, мысалы, су бетімен таралған толқындар да, дыбыс толқындары да интерференцияланады. Егер бірнеше толқындардың фазалары бірдей болса, онда мұндай толқындар бірін-бірі күшейтеді де, ал фазалары қарама-қарсы болса, онда бірін-бірі әлсіретеді.
Осындай интерференциялық көріністер байқалу үшін кеңістіктің әрбір үктесінде қосылатын толқындар фазаларының айырмасы бақылау кезінде өзгермей тұрақты болуы керек. Сондықтан фазалар айырмасы уақытқа байланысты өзгермейтін толқындар когеренттік толқындар деп аталады.
2. 2. Юнг тәжірибесі
Ағылшын физигі Т. Юнг алғаш рет (1802 ж. ) тәжірибе жасап, когерент жарық толқындарының интерференциясын бақылады.
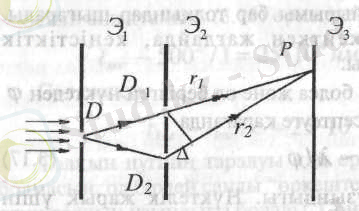 Юнг өз тәжірибесінде (5-сурет) мөлдір емес D тар саңылауы бар Э
1
экранды интенсивті жарықпен сәулелендірді. Сонда одан өткен бытыраңқы жарық шоғы кішкене екі саңылауы бар Э
2
экранға түскен,
Юнг өз тәжірибесінде (5-сурет) мөлдір емес D тар саңылауы бар Э
1
экранды интенсивті жарықпен сәулелендірді. Сонда одан өткен бытыраңқы жарық шоғы кішкене екі саңылауы бар Э
2
экранға түскен,
5-сурет.
одан соң D
1
және D
2
саңылауларынан өткен жарық Э
3
экранға түскен, сонда экранның бетінде жарық және қарақоңыр жолақтар, яғни интерференциялық бейнелер -суреттер байқалған. Э
3
экранның Р нүктесіне зер салсақ, D
1
және D
2
саңылауларынан бір езгілде шыққан сәулелер әртүрлі r
1
<r
2
жол жүріп жетеді. D
1
және D
2
саңылауларынан шығатын тербелістерді оған түскен бір ғана толқын қоздыратын болғандықтан, олардың фазалары бірдей, ал амплитудалары тең болады. D
1
және D
2
саңылауларынан таралып тұрған толқындар когеренттік және де ол толқындардың Э
3
экранының Р нүктесіне жеткенде жол айырымдары
 бүтін не жұп жарты толқын ұзындығына тең болса, онда жарық толқындары Р нүктесінде қосылғанда бірін- бірі күшейтеді:
бүтін не жұп жарты толқын ұзындығына тең болса, онда жарық толқындары Р нүктесінде қосылғанда бірін- бірі күшейтеді:
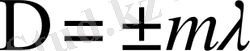 (2. 1)
(2. 1)
мұндағы m=0, 1, 2, 3 . . . ,
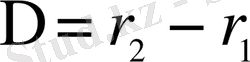
Егер оптикалық жол айырымы
 тақ санды жарты толқынға тең болса, онда олардың тербелістерінің фазалары қарама-қарсы болып, жарық толқындары бірін-бірі өшіреді:
тақ санды жарты толқынға тең болса, онда олардың тербелістерінің фазалары қарама-қарсы болып, жарық толқындары бірін-бірі өшіреді:
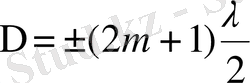 (2. 2)
(2. 2)
 мұндағы m=0, 1, 2, 3 . . .
мұндағы m=0, 1, 2, 3 . . .
S
1
және S
2
тар саңылаулардан пайда болған екі когеренттік жарық толқындарын қарастырайық. Олардың ара қашықтығы d. Р нүктесіне келетін жарық толқындарының
 жол айырымын анықтайық. Ол нүкте экранның ортасынан х қашықтыққа орналасқан. 6-суретте біз S
1
және S
2
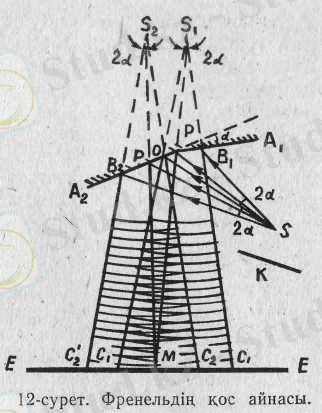
-ге перпендикуляр орналасқан экран жазықтығында жатқан х өсін алдық. О нүктесінде координатаның бас нүктесі орналасқан, d мен x қашықтықтарын өте аз шамалар деп есептеп, жуықтап мына теңдікті аламыз:
жол айырымын анықтайық. Ол нүкте экранның ортасынан х қашықтыққа орналасқан. 6-суретте біз S
1
және S
2
-ге перпендикуляр орналасқан экран жазықтығында жатқан х өсін алдық. О нүктесінде координатаның бас нүктесі орналасқан, d мен x қашықтықтарын өте аз шамалар деп есептеп, жуықтап мына теңдікті аламыз:
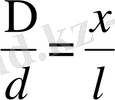
6-сурет. Френельдің қос айнасы.
мұнан
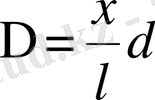 (2. 3)
(2. 3)
(2. 1) теңдеуіндегі
 -ның орнына (2. 3) өрнегін қойсақ:
-ның орнына (2. 3) өрнегін қойсақ:
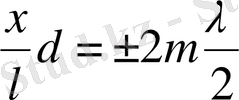 (2. 4)
(2. 4)
бұл теңдіктен максимум интенсивтілік (жарықтың бірін-бірі күшейтуі) х-тің төмендегідей мәнінде байқалады.
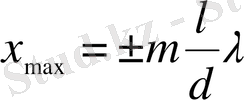 (2. 5)
(2. 5)
мұндағы m=0, 1, 2, 3 . . . ; х-экран орналасқан жарық жолаққа дейінгі қашықтық. .
минимум интенсивтілік үшін (2. 5) үшін теңдеуін мына түрде жазамыз:
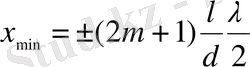 (2. 6)
(2. 6)
мұндағы m=0, 1, 2, 3 . . . ;
2. 3. Френель тәжірибесі
- Қос айнамен жасалған тәжірибе.
Дербес екі жарық көзінен (екі элетр шамынан, екі екі шамнан т. т. ) таралған жарық шоқтары когерент бола алмайтындығы жоғарыда айтылды. Сөйткенмен бір жарық көзінен таралған жарықты шағылу құбылысын пайдаланып, екі шоққа айырып, когерентжарық шоқтарын алуға болады. Френель ең алғаш (1818 ж. ) жазық айналарды пайдаланып осы
 пікірді іске асырды. Оның тәжірибесінің сызбанұсқасы 7-суретте көрсетілген.
пікірді іске асырды. Оның тәжірибесінің сызбанұсқасы 7-суретте көрсетілген.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz