Элементарлық алгебрада қолданылуы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:

Мазмұны

Кіріспе . . . 3

Негізгі бөлім

І БӨЛІМ: х және у бойынша алынған симметриялық көпмүшеліктер

1. 1. Симметриялық көпмүшеліктерге келтірілетін мысалдар . . . 4

1. 2. Екі айнымалысы бойынша симметриялық көпмүшеліктер туралы негізгі теорема . . . 11

1. 3. және арқылы дәрежелік қосындыларды өрнектеу . . . 15

1. 4 . Негізгі теореманың дәлелденуі. . . . 19

ІІ БӨЛІМ: Элементарлық алгебрада қолданылуы

2. 1. Теңдеулер жүйесінің шығарылуы . . . 30

2. 2. Қосымша бегісіздерді енгізу . . . 31

2. 3. Квадрат теңдеулер туралы есептер . . . 35

2. 4. Қайтарымды теңдеулер . . . 37

2. 5. Симметриялық көпмүшеліктерді көбейткіштерге жіктеу . . . 40

2. 6. Әртүрлі есептер . . . 50

Қорытынды . . . 49

Пайдаланылған әдебиеттер тізімі . . . 51

Кіріспе

Табиғатта, техникада және тұрмыста кейбір денелердің өзара ұқсас, үйлесімді орналасуын симметрия деп атайды. «Симметрия» грек сөзінен алынған «үйлесім» сөзі сияқты бірдей өлшемділікті, белгілі бір реттілікпен орналасқан деген ұғымды білдіреді.

Симметрия ұғымымен барлық жерде - табиғатта, техникада, өнерде, ғылымда жиі ұшырасамыз. Симметрия ұғымы адам шығармашылығының көпғасырлық тарихымен тығыз байланысты. Симметрия принцпі физика мен математикада, химия мен биологияда, техника және архитектурада, поэзия мен музыкада маңызды роль атқарады.

Симметрия табиғаттың негізгі фундаментальды қасиеті болып табылады. Ескерткіштерді археологиялық зерттеулер нәтижесі адамзаттың мәдениетінің қалыптаса бастаған кезеңінен бері олардың симметрия туралы ұғым болғанын және суреттер мен тұрмыстық заттарында бейнелеп көрсете білгенін дәлелдеді. Өзінің барлық өмірін симметрияны зерттеуге арнаған академик А. В. Шубников (1887 - 1970) симметрияны алғашқы өндірісте қолану тек эстетикалық мотивке негіделмеген, сондай-ақ белгілі мөлшерде дұрыс формаларды практикада қолданудың жарамдылығына деген адамның сенімділігіне де байланысты болған деген ұйғарым жасады.

Симметрия органикалық емес, әлем мен тірі табиғатта түрлі құрылымдар кездеседі және маңызды рольге ие.

Симметрия әр түрлі болады. Симметрияның ең қарапайым түрі - түзуге қатысты симметрия. Егер түзу бойымен бүктегенде жазықтықтағы екі фигура бір-бірімен беттесетін болса, ондай фигуралар түзуге қатысты симметриялы фигуралар деп аталады.

Симметриялы фигуралар өзара тең болады.

Егер түзу фигураны симметриялы екі бөлікке бөлсе, онда ондай фигура осьтік симметриялы фигура деп аталады, ал түзу сол фигураның симметрия осі деп аталады. Тік төртбұрыш, квадрат, шеңбер - осьтік симметриялы фигуралар. Тік төртбұрыштың екі симметрия осі бар, квадраттың төрт симметрия осі бар. Шеңбердің кез келген диаметрі арқылы өтетін түзу оның симметрия осі болады. Сондықтан шеңбердің симметрия осьтері шексіз көп. Бұрыш - осьтік симмтриялы фигура. Бұрыштың симметрия осі бойындағы бұрыштың төбесінен басталатын сәулені биссектриса деп атайды. Бұрыштың биссектрисасы оны градустық өлшемтері тең екі бұрышқа бөледі.

Симметрияның екінші түрі - нүктеге қатысты симметрия.

О нүктесіне қатысты симметриялы нүктелер фигураның өзінде жатса, ол фигура центрлік симметриялы фигура деп аталады. О нүктесі фигураның симметрия центрі деп аталады. Тік төртбұрыш, шеңбер, кесінді - центрлік симметриялы фигуралар. Тік төрт бұрыштың қарама-қарсы төбелерін қосатын кесінді диагональ деп аталады. Тік төртбұрыштың диагональдарының қиылысу нүктесі - оның симметрия центрі. Шеңбердің симметрия центрі - шеңбердің центрі болатын О нүктесі. Кесіндіні тең екі бөлікке бөлетін О нүктесі - оның симметрия центрі.

Координаталық жазықтықтағы координаталар басы О нүктесіне катысты симметриялы нүктелердің координаталары қарама-қарсы сандар болады.

Табиғатта симметрияның 2 түрі «билатеральды» және «радиальды» кездеседі. 19 ғасырдың зерттеулер нәтижесінде Жердің тарту күші әсерінен табиғаттағы формалар әрбір нүктесінде конустық симметриялы болатыны жөнінде айтылған болатын. Табиғаттағы денелер формасы осы заңға бағынады: «Өсетін немесе вертикаль қозғалатындар, яғни жер бетіне қатысты жоғары-төмен қозғалатындар «радиальды» симметрияға, ал жер бетіне қатысты горизанталь өсетін немесе қозғалатындар «билатеральды» симметрияға бағынады.

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

Оқушыларға алгебрадағы ең қиын бөлімдерінің бірі жоғары дәрежелі теңдеулер жүйесін шығару болып табылады.

Бір белгісізбен квадраттық теңдеулер үшін

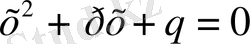
стандартты түрін көрсететін мынадай формула шығады:

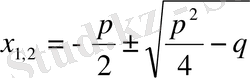Бірінші дәрежелі теңдеулер үшін де стандартты түрде шығарылуы бар (белгісізді жою, коэффициенттердің теңдігі және т. б. ) . Бірақ жоғары дәрежелі теңдеулерді шығару үшін қиынырақ болады.

Көбінесе мұндай жүйелерді шығарғанда белгісіздерді жою әдісі қолданылады. Келесі мысалда бұл әдіс көрсетіледі:

{

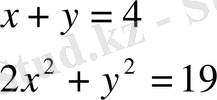
Бірінші теңдеуде у-ті х арқылы өрнектейік. Біз y=4-x таптық. Екінші теңдеуде у-тің орнына 4-х мәнін қояйық, сонда жаңа теңдеуде бір ғана белгісіз х мүшесі шығады:

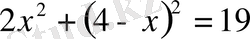
Өрнекті ықшамдағаннан кейін мынадай теңдеу шығады:

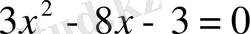Оны шығара отырып, екі түбірін табамыз:

, .

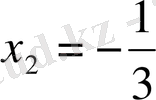Табылған әрбір түбіріне у-тің мәні сәйкес келеді (y=4-x арқылы табылатын) :

, .

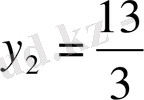Тексеру кезінде жауаптарының екеуі де

{ {

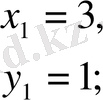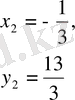
теңдеулер жүйесін қанағаттандыратынын көрсетеді.

Белгісіздерді жою әдісі жалпы болып табылады. Теориялық жағынан қарағанда, кез келген жүйеден екі алгебралық теңдеуде екі белгісіз үшін бір белгісіз мүшені жойып екінші белгісіз мүшесі болатын теңдеуді шығаруға болады. Бірақ белгісіздерді жою әдісі әрқашанда тиімді болмайды. Кейбір жағдайларда белгісіздерді жою әдісі жоғары дәрежелі теңдеулер жүйесіне әкеліп соқтырады (жүйе арқылы шығарылу, қиындық туғызады) . Егер бірінші теңдеулер жүйесінің (екі белгісіз мүшелері болса) дәрежесі n, ал екіншісінің дәрежесі m болса, онда жоюдан кейін, анықтама бойынша, mn дәрежесіндегі теңдеу жоғары алгебрада бар екенін дәлелдейді.

Мысалы, мынадай жүйені алайық

{ .

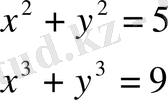Бірінші теңдеуден: 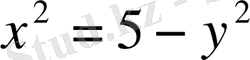табайық, одан

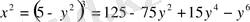Сол сияқты екінші теңдеуден: 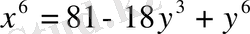шығады.

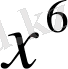үшін екі жағын теңестіріп, тек бір белгісіз у бар теңдеу шығады:

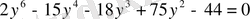Бірақ бұл теңдеу 6-шы дәрежелі ( - жоғары алгебрадағы айтылған теоремаға қатысты), ал формулалар 6-шы дәрежелі теңдеулерді оқушылар шығару үшін қолданылады. Жоқ! Бұл әдіс бізді қиын жолға әкеледі.

Бұл қиындықтар туғанда жою әдісі (жоғары дәрежелі теңдеулер жүйесін шығарғанда) мектепте сирек қолданылады. Көбінесе бұл жүйені жасанды әдіспен шығарады. Бірақ жалпы анықтама бойынша мұндай әдістер қолданылмайды. Әрбір жүйе өзінің тәсілімен шығарылады, және бір жүйені шығару кезінде алынған тәжірибе, екінші жүйені шығару кезінде аз көмек береді. Нәтижесінде мектептегі математикада бұл бөлім оқушыларға өте қиын болып көрінеді және әрбір жүйенің шығару тәсілдері әр түрлі болып келеді.

Бұл дипломдық жұмыста жоғары дәрежелі теңдеулер жүйесінің жалпы шығару әдісінің тиімді жолдары көрсетіледі. Бұл әдістер жою әдісі сияқты барлығына қолданыла бермейді, ол кез келген жүйеге сәйкес келмейді. Бірақ бұл әдісті оқушылар көбінесе барлық жүйелерге қолданылады. Расында да жою әдісімен салыстырғанда бұл әдіс теңдеудің дәрежесін жоғарлатпай, керісінше төмендетеді.

Айтылып отырған әдіс симметриялық көпмүшеліктер теориясына сүйеніп шығарылады. Кез келген адам бұл әдіске қарапт мынадай жағдайларды ескереді: өте жиімді және жеңіл; алгебралық жүйелерді шығаруғы көмектеседі (иррационалдық теңдеулерді шығару, тепе-теңдіктер мен теңсіздіктерді дәлелдеу, көбейткіштерді жіктеу және т. б. ) . Бұл дипломдық жұмыста есептер шығарылып көрсетіледі. Есептердің ішінде күрделі есептер шығарылып, ал кейбіреулері математикалық олимпиадаларда да қолданылады. Симметриялық көпмүшеліктер теориясы көмегімен бұл күрделі есептердің шығару жолы жеңілдетіледі, стандарт түрге келеді.

Дипломдық жұмыс екі бөлімнен тұрады. 1-бөлімде нақты сандардың және комплекс сандардың дамуы жайында айтылады. Натурал, бүтін, рационал сандарға амалдар қолдану, сандардың бөлінгіштік белгілері, жай және құрама сандар, ең кіші ортақ еселік, ең үлкен ортақ бөлгіш, олардың қасиеттері талданады.

Рационал сандар жиынының өріс құрайтындығы жайлы қарастырылады. Ондық бөлшектер, шексіз периодты ондық бөлшектерге мысалдар келтіріледі.

Нақты сандар дәләрек айтсақ рационал және иррационал сандар айырмашылығы

Екінші бөлім комплекс сандарға арналады. Комплекс сандардың геометриялық мағынасы, комплекс сандардың алгебралық және тригонометриялық түрлерінің айырмашылығы, әртүрлі мысалдар келтіріледі.

І БӨЛІМ

х және у бойынша алынған симметриялық көпмүшеліктер

1. 1. Симметриялық көпмүшеліктерге келтірілетін мысалдар

В. Б. Лидский, Л. В. Овсяников, А. Н. Тулайкова және М. И. Шабуниннің «Элементарлық математикадан есептер» (М., 1960) кітабынан мысалдар қарастырайық. Солардың ішінде ең күрделілері жоғарғы дәрежелі теңдеулер жүцелерін таптық.

Мысалы:

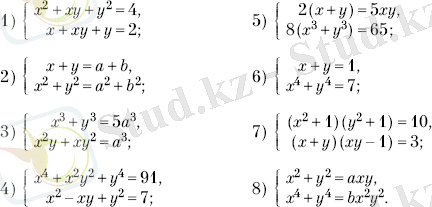
Бұл барлық жүйелердің бір жалпы қаситі - x және y бірдей кіретін сол жақтарында көпмүшеліктер бар теңдеулер. Сондай теңдеулер жүйесіне мынадай тәсілдер қолданылады.

X және y бірдей кіретін көпмүшеліктер симметриялық көпмүшеліктер деп аталады. Яғни,

x және y бойынша көпмүшеліктер симметриялық көпмүшеліктер дейміз, егер

x-ті y-пен, ал y-ті x-пен алмастырғанда өзгермейтін болса.

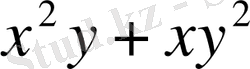- симметриялық көпмүшелік, ал 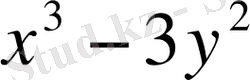- симметриялық көпмүшелік болмайды. X-ті y-пен, ал y-ті x-пен алмастыратын болсақ, ло мына түрге келеді бұл көпмүшелік бастапқыға тең болмайды.

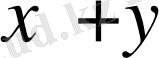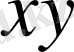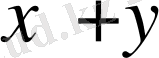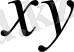Енді негізгі симметриялық көпмүшеліктерге мысалдар келтірейік. Қосылғыштардың орындарын ауыстырғанмен қосындының мәні өзгермейтіні бізге арифметикадан белгілі , мұндағы х, у кез келген сандар. Бұл тепе-теңдік көпмүшелігі симметриялық екенін көрсетеді. Сол сияқты көбейтудің коммутативтік заңдылығы көбейтіндісі симметриялық болатынын көрсетеді. және көпмүшеліктері ең қарапайым симметриялық көпмүшеліктер болып табылады. Оларды 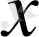және 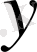бойынша элементарлық симметриялық көпмүшеліктер деп атайды. Оларды және арқылы белгілейді:

, .

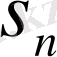және -ден басқа , , . . . , , . . . дәрежелік қосындылыр кездеседі. көпмүшелігін деп белгілеу қалыптасқан. Сонда:

1. 2 Екі айнымалы бойынша симметриялы көпмүшеліктер туралы теорема

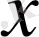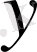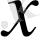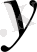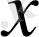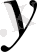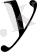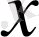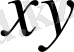Симметриялық көпмүшеліктерді алу үшін жеңіл әдіс бар. Симметриялық емес кез келген және бойынша көпмүшеліктерді алып, және -нің орнына және қояйық. және бойынша симметриялық көпмүшелігі шығатыны белгілі ( , -ті -пен немесе -ті -пен алмастырғаннан және көпмүшеліктері өзгермейді) . Мысалы, 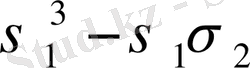көпмүшеліктерінен мынадай симетриялық көпмүшелік шығады:

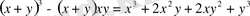Сонымен, және көпмүшеліктерді алып, және -нің орнына , -ті апарып қойсақ, онда 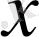және бойынша симмметриялық көпмүшелігі шығады.

Бұл әдіс арқылы кез келген симметриялық көпмүшелікті алуға бола ма? - деген сұрақ туындайды.

Мысалдарды қарастырудан кейін бұл тұжырым ақиқат екеніне көз жеткіземіз. Мысалы, , , , дәрежелік қосындылар және арқылы жеңіл өрнектеледі:

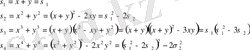
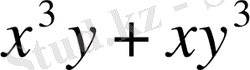симметриялық көпмүшелікті келесі түрге келтірейік:

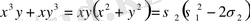Қандай болсын қиын немесе жеңіл симметриялық көпмүшелікті алсақ та, оларды және рақылы өрнектеп шығаруға болады. Осы мысалдардың негізінде келесі теореманың ақиқаттығы шығады:

Теорема. Кез келген және бойынша симметриялық көпмүшеліктерді

және арқылы өрнектеуге болады.

Әрине миллиондаған мысалдар қарастырсақ та, ол бізге дәлелдеудің орнын толықтырмайды.

Математика тарихынан бізге бірнеше қателікті көрсетеді. Француз математигі Пьер Ферма 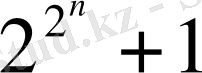сандарын қарастырғанда, 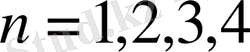болса, онда бұл сандар жай сандар болатынын тауып, енді 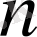кез келген сан болса да жай сан болады деп ұйғарды. Бірақ ол тұжырымды Леонард Эйлер жалған екенін дәлелді. болғанда 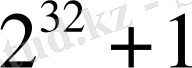онтаңбалы саны шықты, ол жай сан болмайтынын көрсетті (өйткені шыққан сан 641-ге бөлінеді) .

Эйлердің көмегімен көрсетілген басқа мысал. үшмүшелікке 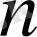-нің орнына 0-ді қойсақ, онда 41 жай саны шығады. болғанда, 43 жай саны шығады. 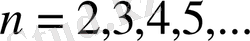сандарын үшмүшелікке қойсақ, жай сандар шыға береді. 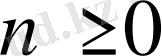кез келген бүтін сандар үшін үшмүшелігі жай сандар үшін орындалады. Бірақ бұл тұжырым да қате! 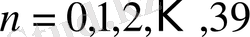сандары үшін шынымен де орындалады. Бірақ 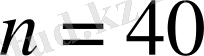болғанда үшмүшеліктің мәні мынадай 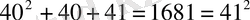бұл сан құрама сан. Бұл мысалдар бізге дәлелдеудің жалпы түрі керектігін көрсетеді. Көрсетілген теореманың дәлелдеуіне келеміз. Оның екі жолмен көрсетеміз.

1. 3 және арқылы дәрежелік қосындыларды өрнектеу

Алдымен симметриялық көпмүшеліктердің кез келгеніне емес, тек дәрежелік қосындыларға қатысты теореманы дәлелдейміз. Басқаша айтқанда, мынаны анықтаймыз

әрбір 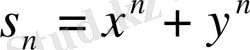дәрежелік қосындыны және арқылы өрнектелген көпмүше түрінде көрсетуге болады.

Сондықтан біз 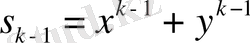теңдеуінің екі жағын да -ге көбейтеміз. Сонда:

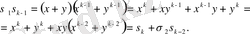
Сонымен,

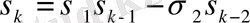. (1)

Бұл формуладан теореманың ақиқаттығы шығады. Шынымен д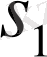е және дәрежелік қосындыларды және арқылы көпмүшеліктерге жіктелетінін біз бұрын да тексердік. 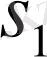, , , , 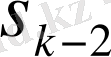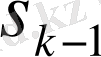дәрежелік қосындылар және арқылы көпмүшеліктерге жіктелетінін білетін болсақ, онда (1) формулаға қойған кезде біз және арқылы өрнектелген дәрежелік қосындыны аламыз. Басқа сөзбен айтқанда, біз 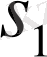және -ні біле отырып және арқылы дәрежелік қосындыларды бірінен соң бірін таба аламыз. (1) формула бойынша 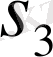-ті табамыз, содан соң , және т. с. с. . Ерте ме кеш пе біз кез келген дәрежелік қосынды үшін және арқылы өрнектелеген өрнекті таба аламыз. Сонымен біздің тұжырымдамамыз дәлелденді.

Дәлелдеменің негізін қалайтын (1) формула дәрежелік қосындыны және арқылы өрнектеуге болатынын ғана емес, сонымен қатар бірінен соң бірін дәрежелік қосындыларды және арқылы есептеп табуға болатынын анықтайды. Сонымен (1) формула арқылы біз бірінен соң бірі мыналарды таба аламыз:

;

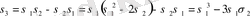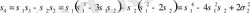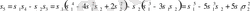және т. б. . 1-кестеде , , , дәрежелік қосындылардың және арқылы өрнектелген түрі берілген. Бүл өрнектерді есеп шығарған үшін қолдануға болады.

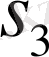
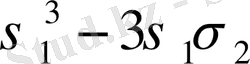
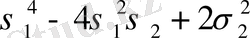
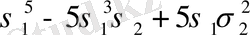
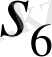
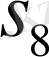
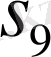
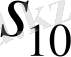
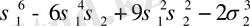
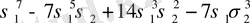
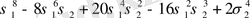
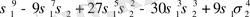
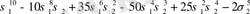
Варинг формуласы. 16 п. дәлелденген (3) формула рекурренттік қатынас болып табылады. S _k дәрежелік қосындының σ ₁ , σ ₂ , σ ₃ арқылы өрнектеуді алғашқы дәрежелік қосындылырды тапқаннан кейін ғана табуға мүмкіндік береді. Бірақ оның көмегімен нақты s _k дәрежелік қосындының өрнегін σ ₁ , σ ₂ , σ ₃ арқылы табуға болады. Бұл өрнек төмендегідей (Варинг формуласы) :

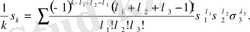
Бұл формулада қосынды барлық теріс емес бүтін λ ₁ , λ ₂ , λ ₃ сандарына ортақ, мұндағы λ ₁ +2λ ₂ +3λ ₃ =k. Егер 0! өрнегі кездескен жағдайда оның мәне 1-ге тең деп аламыз.

λ ₁ +2λ ₂ +3λ ₃ =k,

Варинг формуласындағы λ ₁ , λ ₂ , λ ₃ арқылы өрнектелген қатынасы келесі жағдаймен байланысты. σ ₁ симметриялы көпмүшелігі y, z арқылы өрнектелетін бірінші дәрежелі, σ ₂ - екінші дәрежелі, σ ₃ - үшінші дәрежелі. Сондықтан егер 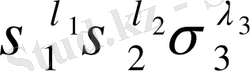бірмүшесіне қарапайым симметриялы σ ₁ , σ ₂ , σ ₃ көпмүшеліктерін x, y, z арқылы өрнектесек, онда x, y, z арқылы өрнектелген дәрежесі λ ₁ +2λ ₂ +3λ ₃ =k болатын біркелкі көпмүшені аламыз. Осыдан s _k дәрежелік қосындысын жіктеуде тек λ ₁ +2λ ₂ +3λ ₃ =k болатын 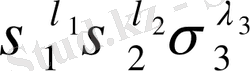бірмүшеліктері кіреді.

Егер (3) байланыспен пайдаланса Варингтiң формуласының дәлелi индукция бойынша өткiзуге қиын емес. Сонымен бiрге келесi оңай қолдануға дәл келедi дәлелделетiн тепе-теңдiк:

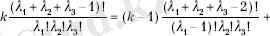
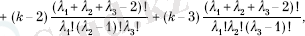
мұндағы, k =λ ₁ +2λ ₂ +3λ ₃ .

Мысал ретiнде қарапайым симметриялық көпмүшелiктер арқылы s ₆ дәрежелi қосындысының өрнегiн табайық. Варингтiң формуласы бойынша алғашқыда теңдеудiң әр түрлi терiс емес шешiмдерін алуы керек

λ ₁ +2λ ₂ +3λ ₃ =6.

4-кестеде көрсетілгендей бұл теңдеудің жеті шешімі болады:

4-кесте

Сондықтан

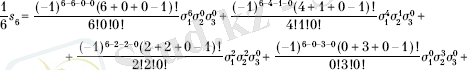
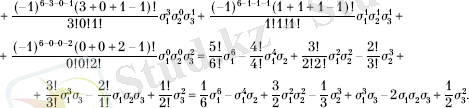
6-ға көбейтіп, келесі түрін аламыз:

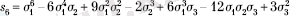
Қайтарымды теңдеулер . Симметриялық көпмүшелiктерді кейбiр

жоғары дәрежелі теңдеулерiнiң шешiмi табу үшiн қолдану мүмкiн. Бұл бөлімде біз қайтарымды теңдеулерді қарастырамыз.

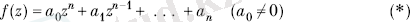
көпмүшесін қайтарымды деп атайық, егер оның шеткі коэффициенттері сәйкес келсе, яғни a ₀ =a _n , a ₁ =a _n-1 , a ₂ =a _n-2 , … Мысалы, қайтарымды көпмүшеліктер мыналар болып табылады

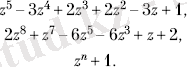
Сол жақ бөлігі қайтарымды көпмүшелік болып табылатын f(z) =0 теңдеуін қайтарымды дейміз.

Қайтарымды теңдеуді шешудің негізі мынада

Теорема. Барлық қайтарымды көпмүшеліктер

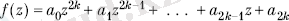
2k жұп дәрежелі келесі түрде беріледі

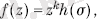
мұндағы, 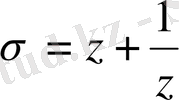және 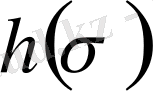- қандайда бір ό-дан k бойынша алынған көпмүшелік.

Барлық қайтарымды f(z) теріс дәрежелі көпмүшелік -ге бөлінеді де, бөлінді жұп дәрежелі қайтарымды көпмүшеге айналады.

Дәлелдеуі.

І БӨЛІМ

Натурал, бүтін, рационал, нақты сандар

1. 1. Cан ұғымының дамуы. Санау жүйесі

Карл Гаусс математиканың сан салаларына сарапқа сала келіп арифметиканы математиканың патшасы деп бағалаған. Ал арифметиканың негізгі ұғымы - сан. Ендеше, сол сан ұғымының қалай пайда болуын ашу, білу - ғылыми методологиялық үлкен мәселе.

Сан туралы ұғым адамзат мәдениетінің тууымен және оның дамуымен тығыз байланысты. Шынында, егер осы ұғым болмаса, өзіміздің рухани өміріміз бен практикалық қызметімізді тиісті дәрежеде көрсете алмас едік. Есеп - қисап жүргізу, уақыт пен қашықтықты өлшеу, еңбек нәтижесінің қорытындысын есептеу сан ұғымынсыз мүмкін емес.

Сан әуел баста заттарды санаудың қажеттілігінен туған математикалы ұғымдардың бірі. Кейін ол математикалық білімнің дауына қарай жетілдірілді. Бұл ұғым өте ерте заманда адамдардың практикалық қызметтерінінен қажеттілігінен келіп туды.

Сан- әуел баста заттарды санаудың қажеттілігінен туған негізгі математикалық ұғымдардың бірі. Кейін ол математикалық білімдердің дамуына қарай жетілдірілді.

Бұл ұғым өте ерте заманда, күллі математика ғылымы сияқты адамдардың практикалық қызметінің қажеттілігінен келіп туды. Ол өте баяу қалыптасты, сөйтіп, барған сайын күрделене түскен әуелі практикалық, ал сонан соң теориялық сипаттағы мәселелерді шешу барысында көптеген ғасырлар бойы біртіндеп кеңейіп және жалпыланып отырды.

Нәрселерді санаудың нәтижесінде натурал сандар шыққан. Натурал сандырдың әрқайсысын белгілеу үшін жасалған таңбалар цифрлар деп аталады.

Цифрлар: 1, 2, 3, 4, 5, 6, 7, 8, 9, және 0. Бұл цифрлар алғашқыда Үнді (Индия) елінде қолданылған, бірақ Еуропаға бұл цифрлардың арабтар әкелген. Осыдан бұл цифрлар араб цифрлары деп аталған.

Осындай цифрлардан сандар құрастырылып, олар белгілі бір тәсілмен аталып таңбаланған.

Натурал сан ұғымының дамуы ерте заманда адамның заттар жиынтығының санын оларды санамай-ақ, яғни өзара бір мәнді сәйкестікті тағайындай негізінде қабылданумен сипатталады. Өте ұзақ санаудың нәтижесінде адам натурал сандарды жасаудың келесі кезеңіне жетті - жиындарды салыстыру үшін аралық жиындарды қолдана бастады. Бұл кезеңде сан саналатын жиындардан ерекшеленген жоқ. Адам аралық жиындарды қолдануға үйренгеннен кейін барып қана объектілер мен аралық жиындар арасындағы ортақ нәрсені анықтады.

Аралық жиындарды, оның элементтері табиғатынан дерексіздендіру мүмкін болғаннан кейін натурал сан туралы түсіні пайда болды.

Уақыт өте келе адамдар сандарды атауды ғана емес, оларды белгілеуді де, сондай-ақ олармен амалдар орындауды да үйренді. Осындай мәселелерді шешудегі көптеген қиыншылықтар Ежелгі Үндістанда сандардың ондық жазуы мен нөл ұғымының жасалуы нәтижесінде ғана жойылды. Әуелде санның жоқтығын білдірген нөл теріс сандар ұғымы енгізілгеннен кейін ғана сан ретінде қарастырылатын болды. Натурал сандар жиынының шексіздігі туралы түсінік біртіндеп қалыптасты. “Натурал сан” терминін тұңғыш рет римдік ғалым А. Боэций (шамамен 480-524 жылдар) қолданған. Санаудың ондық жүйесі қазіргі түрінде біздің заманымыздың VI ғасырында Үндістанда қалыптасты. Нөл үшін ерекше белгі енгізу үндістандықмаңызды жетістігі болды. Нөл енгізілгеннен кейін ғана жазудың ондық жүйесі толығымен аяқталды. Алдымен нөлдің абактың тиісті разрядында тастардың жоқтығын белгілеу үшін пайда болуы да ықтимал.

Натурал сан ұғымы қалыптасқаннан кейін сандар дербес объектілерге айналды және оларды математикалық объектілер ретінде зерттеудің мүмкіндігі пайда болды. Арифметика - сандарды және оларға қолданатын амалдарды зерттейтін ғымым, ол Ежелгі Шығыс елдерінде: Вавилонда, Қытайда, Үндістанда, Египетте дүниеге келді. Осы елдерде жинақталған математикалық білімдерді Ежелгі Грецияның ғалымдары дамытып, жалғастырды. Орта ғасырда арифметиканың дамуына Үндістанның, араб елдері мен Орта Азия математикатері, ал XIII ғасырдан бастап - европалық ғалымдар үлкен үлес қосты.

Сөйтіп, ежелгі дүние ғалымдары еңбектерінің өзінде-ақ натурал сандар қатарының шексіздігі анықталды. (біздің дәуірге дейінгі ІІІ ғ. ) .

XIX ғасырда ғалымдардың назары натурал санның математикалық теорияларын, яғни натурал сандармен есептеулер жүргізуге негіз болған теорияларды құруға және логикалық тұрғыдан негіздеуге аударылды. Санның натурал қатарындағы терең заңдылықтарды зерттеу қазіргі уақытқа дейін жалғастырылып, сандар теориясын да қамтуда. Натурал сандар ұғымының өте қарапайым және табиғи көрінетіні сондай, ғылымда ұзақ уақыт бойы оны қандай да болсын қарапайым ұғымдардың терминдерімен анықтау туралы мәселе қойылған жоқ.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.