Екінші ретті сызықтық біртекті дифференциалдық теңдеулер: бірінші ретті туындыдан құтылу әдістері, ретті төмендету, Риккати байланысы және жалпыланған дәрежелік қатарлар


Мазмұны
Кіріспе . . . 3
1 Функцияның бірінші ретті туындысынан құтылуға болатын теңдеулер . . . 6
1. 1 Түйіндесіне келтіру әдісі . . . 9
1. 2 Ретін төмендету әдісі . . . 11
2 Екінші ретті сызықтық біртекті теңдеулердің кейбір ерекшеліктері
2. 1 Екінші ретті сызықтық біртекті теңдеумен Риккати теңдеуінің арасындағы байланыс . . . 14
2. 2 Екінші ретті теңдеулерді дәрежелік қатарлар арқылы интегралдау . . . 15
2. 3 Ерекше нүктелердің маңайындағы шешімдерді жалпыланған дәрежелік қатар түрінде көрсету . . . 16
3 Бессель теңдеуі . . . 28
Қорытынды . . . 40
Қолданылған әдебиеттер . . . 41
Кіріспе
Математиканың физикалық, химиялық және т. б. құбылыстарды өзгеру заңдылығы емес, олардың өзгеру жылдамдығының заңдылығы белгілі болуына байланысты, дифференциалдық теңдеулерді зертеуге алып келеді, яғни функцияның туындысы (құбылыстың өзгеру жылдамдығы) белгілі болғанда, осы функцияның өзінің аналитикалық түрін анықтап, дифференциалдық теңдеулер теориясының негізгі мәселесі болып табылады.
Дифференциалдық теңдеулер теориясына байланысты мәселелер мен есептер XVI - XVII ғасырлар тұсында пайда болған, әсіресе ол логарифмдік таблицаларды жасау үшін есептеу математикасы тарауында көп кездескен.
Кедергісіз ортада құлап түсетін ауыр дененің қозғалысын зерттегенде дифферециалдық теңдеулерге келтірілетін есептерді алғаш рет Г. Галилей (1564 - 1642) шешкен.
Жарық сәулелерінің сыну заңын аша отырып Р. Декарт (1596 - 1650) «Жанамаларға кері есептерді» 1628 жылы шешкен.
Дифференциалдық теңдеулер теориясының алғашқы даму кезеңі И. Ньютон (1642 - 1727) және Г. В. Лейбниц (1646 - 1716) еңбектерімен тығыз байланысты, олар қатты денелермен нүктелер динамикасын зерттеп, 1 - және 2 - ретті дифференциалдық теңдеулер алған.
Осылайша дамудың арқасында XVIII ғасырдың екінші жартысында дифференциалдық теңдеуді тек механикада ғана емес, дифференциалдық геометрия және вариациялық есептеулер, ал XVIII ғасырдың аяғына таман математикалық физикада және тағы басқа салаларда, ал қазір ғылым мен техниканың барлық салаларын зерттеуде қолданылатын дәрежеге жеткен.
Жаратылыстану ғылымдарындағы ең негізгі мәселелердің бірі - өзімізді қоршап тұрған табиғат құбылыстарындағы неше қилы үрдістерді зерттеу.
Оны зерттеу үшін болатын құбылысты, оның бүкіл ағымын, әрбір мезгілдегі күйінің өзгеру және оны туғызушы себептердің пайда болу заңдылығын білу қажет.
Осы айтылып отырған негізгі мәселелерді шешуде математиканың қолданылатын салаларының бірі - дифференциалдық теңдеулер .
Бұл пәннің бір ерекшелігі - жоғарыда айтылған табиғат құбылыстары, оның күлі өзгеруі, қозғалысы негізінен дифференциалдық теңдеулер арқылы бейнеленіп, солардың көмегі арқылы зерттеледі.
Сондықтан дифференциалдық теңдеулер пәні теориялық маңыздылығымен бірге қолданбалы математика саласына да жатады. Сол себептен де ол жаратылыстану ғылымы мен техниканың көптеген мәселелерін зерттейді.
Өйткені, механиканың, астрономияның, физиканың, химияның, биологияның, космостық зерттеулердің көптеген мәселелері дифференциалдық теңдеу не жүйе құрып, оның шешімдерін табуға тіреледі.
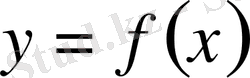 функциясымен және олардың
функциясымен және олардың
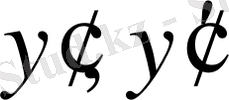 туындыларымен x - аргументімен байланыстыратын теңдеуді
дифференциалдық теңдеу
деп атаймыз.
туындыларымен x - аргументімен байланыстыратын теңдеуді
дифференциалдық теңдеу
деп атаймыз.
Берілген дифференциалдық теңдеудің реті деп сол теңдеудің құрамындағы ең жоғарғы реті туынды.
Берілген дифференциалдық теңдеудің шешімі немесе интегралы деп сол функцияның туындысы мен теңдеудегі мәніне қойғанда теңдеу тепе - теңдікке айналады.
Теңдеумен қоса бастапқы шарт
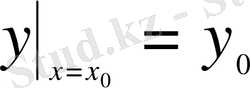 берілсе, онда ол теңдеуді Коши есебі деп атайды.
берілсе, онда ол теңдеуді Коши есебі деп атайды.
Дифференциалдық теңдеудің ең қарапайымы айнымалылары бөлектенген
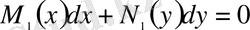 және айнымалылары бөлектенетін
және айнымалылары бөлектенетін
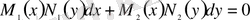 теңдеулер.
теңдеулер.
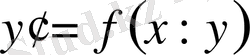 теңдеуінің оң жағындағы 0 - өлшемдегі біртекті функция болса, онда бұл теңдеуді біртекті теңдеу деп атайды.
теңдеуінің оң жағындағы 0 - өлшемдегі біртекті функция болса, онда бұл теңдеуді біртекті теңдеу деп атайды.
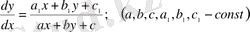 біртекті теңдеуге келтірілетін теңдеу.
біртекті теңдеуге келтірілетін теңдеу.
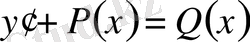 түріндегі берілген теңдеуді сызықтық теңдеу деп атайды.
түріндегі берілген теңдеуді сызықтық теңдеу деп атайды.
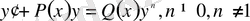 - Бернулли теңдеуі.
- Бернулли теңдеуі.
 - түрдегі теңдеуді Рикатти теңдеуі деп атаймыз.
- түрдегі теңдеуді Рикатти теңдеуі деп атаймыз.
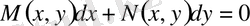 теңдеуі толық дифференциалдағы теңдеу деп аталады.
теңдеуі толық дифференциалдағы теңдеу деп аталады.
Клеро теңдеуі
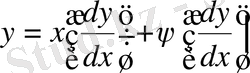 деп атаймыз. Лагранж теңдеуі:
деп атаймыз. Лагранж теңдеуі:
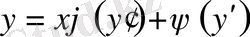 .
.
Жоғарғы ретті дифферециалдық теңдеулер
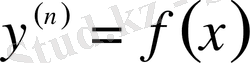 түріндегі теңдеу.
түріндегі теңдеу.
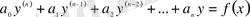 - теңдеуді (n) - ретті сызықтық теңдеу деп атаймыз.
- теңдеуді (n) - ретті сызықтық теңдеу деп атаймыз.
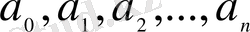 және
және
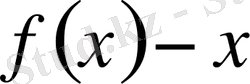 айнымалысының функциясы немесе тұрақты мәндер. Мұндағы,
айнымалысының функциясы немесе тұрақты мәндер. Мұндағы,
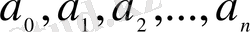 және
және
 - тің барлық мәнінде үзіліссіз функциялар. Мұндағы,
- тің барлық мәнінде үзіліссіз функциялар. Мұндағы,
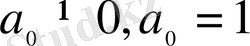 деп алып,
деп алып,
 , онда теңдеуді біртекті сызықтық теңдеу немесе теңдеудің оң жағы жоқ деп аталады. f(x) болса, онда біртекті емес сызықтық теңдеу деп аталады. Тұрақты коэффициенті бар сызықтық біртекті екінші ретті дифференциалдық теңдеу:
, онда теңдеуді біртекті сызықтық теңдеу немесе теңдеудің оң жағы жоқ деп аталады. f(x) болса, онда біртекті емес сызықтық теңдеу деп аталады. Тұрақты коэффициенті бар сызықтық біртекті екінші ретті дифференциалдық теңдеу:
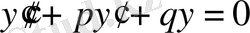 . Тұрақты коэффициенті бар біртекті сызықтық n - ретті дифференциалдық теңдеу:
. Тұрақты коэффициенті бар біртекті сызықтық n - ретті дифференциалдық теңдеу:
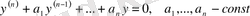 .
.
Одан арғы, біртекті екінші ретті сызықтық теңдеудің кейбір сұрақтары, сонымен қатар, дифференциалдық теңдеудің аналитикалық теория негізінде, жалпыланған дәрежелік қатарларды интегралдаудың сұрақтары қарастырылады, мысал ретінде Бессель теңдеуінің шешімінің құрылуы беріледі. Тағы теңдеудің көбісін квадратуралар да интегралдауға мүмкіндігі бар екені көрсетіледі.
Дегенмен де, атап кету керек, квадратураларда интегралданатын теңдеулер, барлық дифференциалдық теңдеулердің кішігірім бөлігін ғана құрастырады.
Мысалы, көп сұрақтардағы өте маңызды Бессель теңдеуі
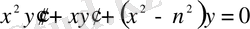
жалпы жағдайда квадратурада интегралданбайды.
Дифференциалдық теңдеудің жалпыланған теориясының міндеті кез келген берілген дифференциалдық теңдеудің түрі бойынша тікелей дифференциалдық теңдеумен анықталатын функцияның қасиеттерін зерттеу.
1 Функцияның бірінші ретті туындысынан құтылуға болатын теңдеулер
Біртекті екінші ретті сызықтық теңдеулердің шешудің қасиеттерін зерттеуде және жауаптарын табуесептерінде көбінесе теңдеуді кейбір арнайы формаға келтіру әдістері пайдалы. Келесі теңдеуді қарастырайық.
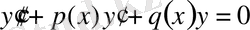 (1)
(1)
теңдеуді әрдайым бірінші ретті туындысы жоқ түрдегі теңдеуге келтіруге болады.
Ол үшін
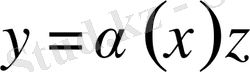 (2)
(2)
Мұндағы z - жаңа ізделінді екінші ретті үзіліссіз дифференциалданатын функция
(2) - теңдеуді (1) - теңдеуге қойып,
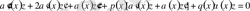
немесе
 (3)
(3)
теңдеуін аламыз.
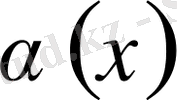 -ті:
-ті:
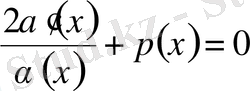 (4)
(4)
теңдеуінің шешімі
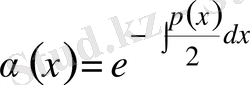 (5)
(5)
деп алғанда,
 коэффициенті 0-ге айналады.
коэффициенті 0-ге айналады.
Расында
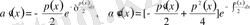
сонда, (3) -теңдеуі мына түрге келеді:
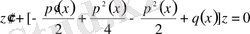 (6)
(6)
Сөйтіп, ізделінді функцияның сызықтық алмастыруы
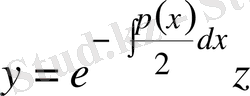 (7)
(7)
теңдеуді (1) түрге келтіреді:
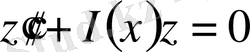 (8)
(8)
Мұнда
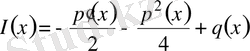 (9)
(9)
 функциясы (1) - теңдеудің инварианты деп аталады.
функциясы (1) - теңдеудің инварианты деп аталады.
Егер (8) - теңдеу квадратурада интегралданса, онда (1) - теңдеу де квадратурада интегралданады.
Мысалы
, егер
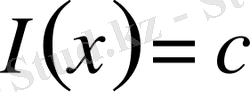 немесе
немесе
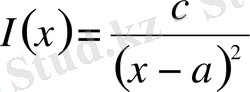 болса, бұл сөз орын алады. Өйткені бұл жерде (1) - теңдеу тұрақты коэффициентті теңдеуге келтіріледі немесе Эйлердің сызықтық теңдеуіне келтіріледі.
болса, бұл сөз орын алады. Өйткені бұл жерде (1) - теңдеу тұрақты коэффициентті теңдеуге келтіріледі немесе Эйлердің сызықтық теңдеуіне келтіріледі.
Тұрақты коэффициенті бар теңдеу үшін инвариант характиристикалық теңдеудің дискриминантын қарама - қарсы таңбамен алу дегенді білдіреді.
1 - мысал: Бессель теңдеуін қарастырамыз:
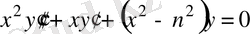 (10)
(10)
Мұндағы
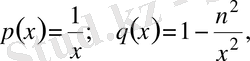
Сондықтан
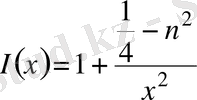 (11)
(11)
бұдан,
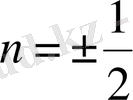 болса, орнына қойғанда
болса, орнына қойғанда
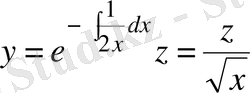 (12)
(12)
Бессел теңдеуін
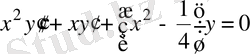 (13)
(13)
мына теңдеуге келтіреді
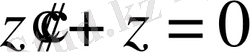 (14)
(14)
 болғандықтан, бұл теңдеудің тәуелсіз дербес шешімінің мағынасы,
болғандықтан, бұл теңдеудің тәуелсіз дербес шешімінің мағынасы,
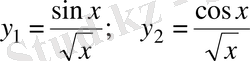 (15)
(15)
 болған жағдайда, бұл шешімдердің екіншісі x=0 ерекше нүктесінде
болған жағдайда, бұл шешімдердің екіншісі x=0 ерекше нүктесінде
 ұмтылатын ерекшелігі бар.
ұмтылатын ерекшелігі бар.
(15) - шешімді
 көбейте отырып, Бессель функциясын аламыз
көбейте отырып, Бессель функциясын аламыз
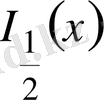 және
және
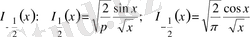 (16)
(16)
(13) - теңдеудің жалпы шешімі мына түрге келеді:
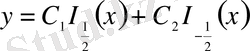 (17)
(17)
2 - мысал: Теңдеудің жалпы шешімін табу
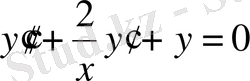 (18)
(18)
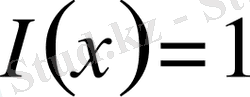 болғандықтан,
болғандықтан,
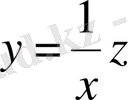 қойып,
қойып,
 теңдеуін аламыз. Сондықтан (18) - теңдеудің жалпы шешімі мына түрде болады:
теңдеуін аламыз. Сондықтан (18) - теңдеудің жалпы шешімі мына түрде болады:
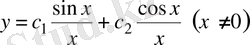 (19)
(19)
1. 1 Түйіндесіне келтіру әдісі
Біртектес екінші ретті сызықтық теңдеудегі
 туындысындағы коэффициент
туындысындағы коэффициент
 туындысындағы коэффициентке тең болсын:
туындысындағы коэффициентке тең болсын:
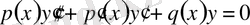 немесе
немесе
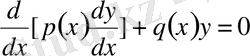 (20)
(20)
Мұндағы
 және
және
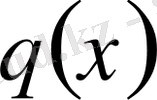 - x -ке тәуелді функциялары екінші ретті өзіне түйіндес теңдеуі деп аталады. Өзіне түйіндес формадағы теңдеу, мысалы, аймақты есептер теориясында қолданылады.
- x -ке тәуелді функциялары екінші ретті өзіне түйіндес теңдеуі деп аталады. Өзіне түйіндес формадағы теңдеу, мысалы, аймақты есептер теориясында қолданылады.
Кез келген екінші ретті сызықтық теңдеу
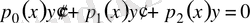 (21)
(21)
 интервалында коэффициенттері үздіксіз, және де
интервалында коэффициенттері үздіксіз, және де
 , түріне әрдайым келтіруге болады.
, түріне әрдайым келтіруге болады.
Расында да, (21) - теңдеудің екінші жағын
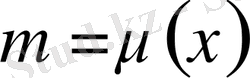 функциясына көбейтеміз:
функциясына көбейтеміз:
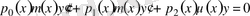 (22)
(22)
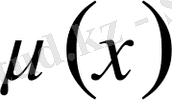 таңдап аламыз
таңдап аламыз
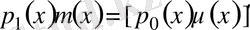 (23)
(23)
бұл теңдеуді мына түрде жазамыз:
 (24)
(24)
Бұл біртектес бірінші ретті сызықтық теңдеуді интегралдап:
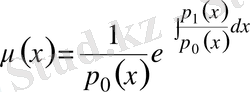 (25)
(25)
табамыз.
Сонда (22) - теңдеуі былай жазылады:
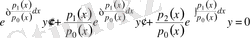 (26)
(26)
Бұл теңдеудің түйіндесі
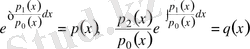 (27)
(27)
деп белгілейміз.
Сонда (26) - теңдеу мына түрге келеді:
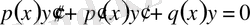 (28)
(28)
немесе
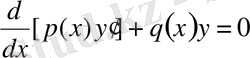 (29)
(29)
мұнда
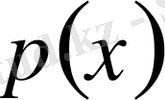 және
және
 функциялары
функциялары
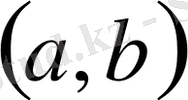 интервалында үзіліссіз, сонымен қатар, егер
интервалында үзіліссіз, сонымен қатар, егер
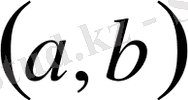 интервалында
интервалында
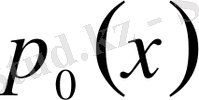 нөлге айналмаса, онда
нөлге айналмаса, онда
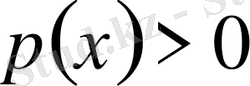 .
.
1 - мысал : Лежандр теңдеуін қарастырамыз
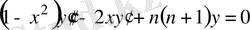 (30)
(30)
x=-1 және x=+1 бұл теңдеудің ерекше нүктелері. Лежандр теңдеуінің (-1; 1) интервалында қарастырамыз, бұл теңдеуд өзіне түйіндес болып келеді, мұндағы
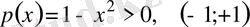 интервалында .
интервалында .
2 - мысал: Бессель теңдеуі берілген:
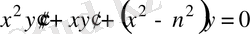 (31)
(31)
бұл теңдеуді
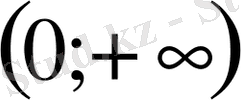 интервалында қарастырамыз.
интервалында қарастырамыз.
(31) - теңдеуді өзіне түйіндес түрге келтіреміз.
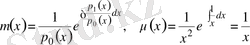 (32)
(32)
Сондықтан Бессель теңдеуі өзіне түйіндес формасында мына түрде жазылады:
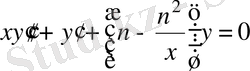 (33)
(33)
немесе
 (34)
(34)
Мұнда
 интервалында қарастырдық.
интервалында қарастырдық.
1. 2 Ретін төмендету әдісі
Бір дербес шешімі белгілі болғанда, екінші ретті сызықтық біртекеті теңдеудің жалпы шешімін құру.
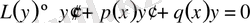 (1)
(1)
теңдеуі берілсін және оның
 - нөлінші емес дербес шешімі белгілі болсын. Онда жаңа енгізілген функцияларға сәйкес, алмастыру
- нөлінші емес дербес шешімі белгілі болсын. Онда жаңа енгізілген функцияларға сәйкес, алмастыру
 (2)
(2)
болады.
мұндағы u - жаңа белгісіз функция.
(2) - алмастыру берілген (1) - теңдеуді бірінші ретті сызықтық біртекті теңдеуге түрлендіреді, яғни (1) - теңдеу квадратураларда интегралданады.
Жалпы шешімінің формуласын енгізейік. (2) - теңдікті (1) - теңдікке қойсақ, шығады:
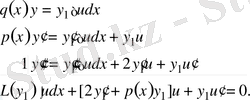 (3)
(3)
Осыдан,
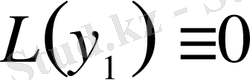 болғандықтан:
болғандықтан:
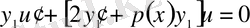 (4)
(4)
немесе
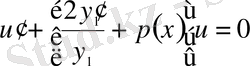 (5)
(5)
болады.
Осы сызықтық теңдеуді интегралдасақ:
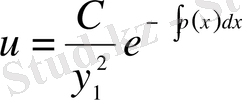 (6)
(6)
С=1 деп алып, табылған u - дің мәнін (2) - формулаға қойсақ, (1) - теңдеудің екінші дербес шешімі келесі формуламен анықталады:
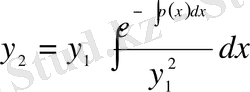 (7)
(7)
Қорыта айтсақ, ізделінді жалпы шешімнің түрі:
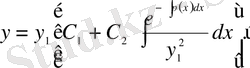 (8)
(8)
Мысал 1. Келесі теңдеудің жалпы шешімін табайық:
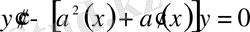 (9)
(9)
бұл теңдеудің дербес шешімі:
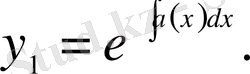 (10)
(10)
Сондықтан
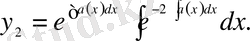 (11)
(11)
(9) - теңдеудің шешімі келесідей болады:
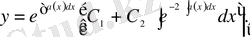 (12)
(12)
Мысал 2. Теңдеудің жалпы шешімін тап
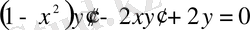 (13)
(13)
Жалпы түрдегі Лежандр теңдеуіндегідей x= -1және x=1 нүктелері берілген теңдеудің ерекше нүктелері болып табылады. (13) - теңдеудің шешімін болжап тауып алуға болады. Ол
 болады.
болады.
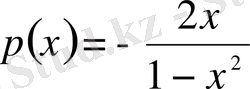 болғандықтан,
болғандықтан,
 (14)
(14)
яғни
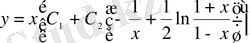 (15)
(15)
(13) - теңдеуінің аралығындағы жалпы шешімі
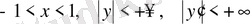 (16)
(16)
Ескерте кету керек x ерекше нүктелерге x= -1 немесе x= 1 - ге ұмтылғанда,
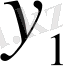 және
және
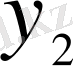 сызықтық тәуелсіз шешімдерінің біреуі ғана шенелген болады, ол
сызықтық тәуелсіз шешімдерінің біреуі ғана шенелген болады, ол
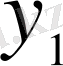 - дербес шешімі. Осы қасиетке жалпы түрдегі Лежандр теңдеуі ие екендігін көрсетуге болады.
- дербес шешімі. Осы қасиетке жалпы түрдегі Лежандр теңдеуі ие екендігін көрсетуге болады.
Ескерту. (7) - формуланы біз тек элементар функция түрінде дербес шешімді білген жағдайда ғана пайдалы емес. Мысалы, екінші ретті сызықтық біртекті теңдеу үшін сызықтық тәуелсіз шешімдерінің аналитикалық құрылымын зерттегенде, бұл формула екі шешімнің біреуінің аналитикалық құрылымына қарап екіншісінің құрылымын анықтауға мүмкіндік береді.
2 Екінші ретті сызықтық біртекті теңдеулердің кейбір ерекшеліктері
2. 1 Екінші ретті сызықтық біртекті теңдеумен Риккати теңдеуінің арасындағы байланыс
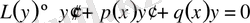 (17)
(17)
теңдеуінің ретін әрдайым бірге төмендетуге болады, егер ізделінді функцияға немесе оның туындыларына қатысты біртекті теңдеулердің ретін төмендету ережесін қолдансақ.
Жаңа белгісіз z функциясын енгізейік және
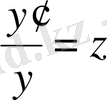 (18)
(18)
болсын.
Онда
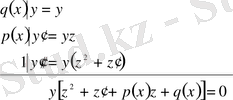 (19)
(19)
y - ке қысқартып, Риккати теңдеуін аламыз:
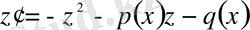 (20)
(20)
Осылайша (18) - формуламен алмастыру кез келген екінші ретті сызықтық біртекті теңдеуді Риккати теңдеуіне түрлендіреді.
Дербес жағдайда:
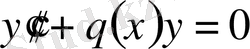 (21)
(21)
түріндегі теңдеу
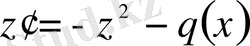 (22)
(22)
түріндегі Риккатидің канондық теңдеуіне түрленеді.
Керісінше, кез келген
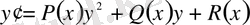 (23)
(23)
түріндегі Риккати теңдеуін екінші ретті сызықтық біртекті теңдеуге түрлендіруге болады.
Осы теңдікте
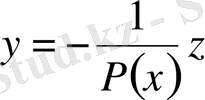 (24)
(24)
деп алсақ, (20) түріндегі Риккати теңдеуін аламыз, ол
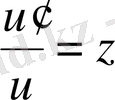 алмастыруы арқылы (17) түрдегі теңдеуге келтіріледі.
алмастыруы арқылы (17) түрдегі теңдеуге келтіріледі.
Осылайша,
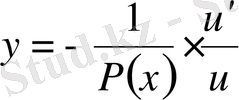 (25)
(25)
алмастыруы, кез келген Риккати теңдеуін (23) екінші ретті сызықтық біртекті теңдеуіне (17) түрлендіреді.
Риккати теңдеуі квадратураларда тек кейбір жағдайларда ғана интегралданады, сондықтан, айнымалы коэффиценттері бар екінші ретті сызықтық біртекті теңдеулерге қатысты сондай сөз айтуға болады.
Екінші ретті сызықтық біртекті теңдеумен Риккати теңдеуінің арасындағы байланыстың маңыздылығы, ол біреуі үшін шешімдерінің қасиеттерін зерттеуді екінші үшін шешімдерінің қасиеттерін зерттеуге алмастыруға көмектеседі.
2. 2 Екінші ретті теңдеулерді дәрежелік қатарлар арқылы интегралдау
 (1)
(1)
теңдеуі берілсін.
мұндағы p(x), q(x) - функциялары
 нүктесінің маңайындағы бас функциялар деп аталады, яғни
нүктесінің маңайындағы бас функциялар деп аталады, яғни
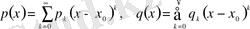 (2)
(2)
сондай - ақ, қатар
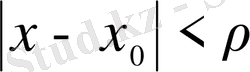 аймағында оң жағынан жинақталады.
аймағында оң жағынан жинақталады.
Олай болса, Коши теоремасы бойынша,
 нүктесінің аймағында және осы аймақта алдын ала берілген
нүктесінің аймағында және осы аймақта алдын ала берілген
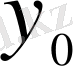 және
және
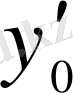 мәндерін қабылдайтын голоморфты жалғыз шешімі болады, яғни шешімінің түрі:
мәндерін қабылдайтын голоморфты жалғыз шешімі болады, яғни шешімінің түрі:
 (3)
(3)
Сондай - ақ, қатар алдын ала оң жағынан,
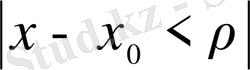 аймағында жинақталады, ал
аймағында жинақталады, ал
 және
және
 алдын ала берілген сандар.
алдын ала берілген сандар.
Қолданыста көбінесе (1) - теңдеудің коэффициенттері көпмүшелер немесе көпмүшелер қатынасы болып келеді.
Бірінші жағдайда шешімі барлық x - те жинақталатын дәрежелік қатар түрінде болады, ал екінші жағдайда теңдеудің шешімі болып келетін дәрежелік қатардың жинақталу аймағы
 - нүктесінен, теңдеу коэффициенттерінде қарастырылып отырған бөлімі нөлге айналдыратын ең жақын нүктелерге дейінгі қашықтықтан кем болмайды.
- нүктесінен, теңдеу коэффициенттерінде қарастырылып отырған бөлімі нөлге айналдыратын ең жақын нүктелерге дейінгі қашықтықтан кем болмайды.
Егер
 және
және
 берілсе, (3) - формуладағы
берілсе, (3) - формуладағы
 - коэффиценттері анықталады. Оларды анықтауға болады, мысалы, (3) - қатарды (1) - ші теңдеуге қойып және сол жақтағы теңдеуде әртүрлі
- коэффиценттері анықталады. Оларды анықтауға болады, мысалы, (3) - қатарды (1) - ші теңдеуге қойып және сол жақтағы теңдеуде әртүрлі
 дәрежелеріндегі коэффициенттерді нөлге теңестіреміз.
дәрежелеріндегі коэффициенттерді нөлге теңестіреміз.
Әдетте,
 нүктесінде нормаланған фундаменталь
нүктесінде нормаланған фундаменталь
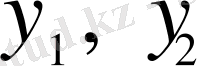 шешімдер жүйесін құрады, яғни
шешімдер жүйесін құрады, яғни
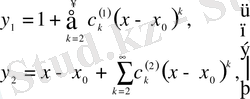 (4)
(4)
осыдан кейін жалпы шешімді
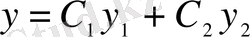 (5)
(5)
формуласымен анықтайды.
2. 3 Ерекше нүктелердің маңайындағы шешімдерді жалпыланған дәрежелік қатар түрінде көрсету
Егер
 нүктесі
нүктесі
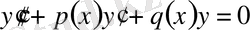 (6)
(6)
теңдеуінің ерекше нүктесі болсын, онда жалпы жағдайда, шешіміде осы нүктенің ешбір аймағында голоморфты болмайды.
Мысалы, Бессель теңдеуінің
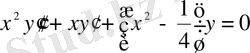 (7)
(7)
ерекше нүктесі x=0. Бұл теңдеудің келесі сызықтық тәуелсіз дербес шешімдері бар:
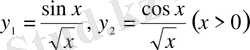 (8)
(8)
Осы дербес шешімдердің ешбіреуі x=0 ерекше нүктесінің ешбір аймағында голоморфты емес, яғни x - тің оң бүтін дәрежесі бойынша қатар түрінде көрсетілмейді. Бірақ, бұл шешімдерді x=0 ерекше нүктесінің аймағында қатарлар түрінде көрсетуге болады,
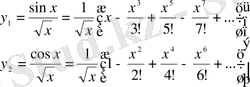 (9)
(9)
немесе
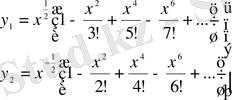 (10)
(10)
олар жалпы дәрежелік қатарлардан өзгешелігі тек x - көбейткішінде. Осындай қатарлар жалпыланған дәрежелік қатарлар деп аталады.
Жалпы (
 айырмасының дәрежесі бойынша ) жалпыланған дәрежелік қатар деп:
айырмасының дәрежесі бойынша ) жалпыланған дәрежелік қатар деп:
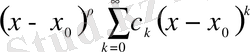 (11)
(11)
мұндағы
 - кез келген тұрақты сан, ал
- кез келген тұрақты сан, ал
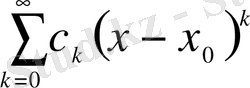 (12)
(12)
қатары
 айырмасының дәрежесі бойынша жинақталатын дәрежелік қатар,
айырмасының дәрежесі бойынша жинақталатын дәрежелік қатар,
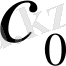 - коэффициенті нөлден өзге.
- коэффициенті нөлден өзге.
Келесі сұрақты қояйық:
(6) - теңдеудің әйтеуір бір дербес шешімі ерекше нүктенің аймағында
 дәрежелері бойынша жалпыланған дәрежелік қатар, яғни
дәрежелері бойынша жалпыланған дәрежелік қатар, яғни
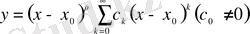 (13)
(13)
түрінде көрсетілуі үшін осы (6) - теңдеудің
 ерекше нүктесінің аймағында коэффициенттері қандай түрде болуы керек.
ерекше нүктесінің аймағында коэффициенттері қандай түрде болуы керек.
Осы сұраққа жауап дифференциалдық теңдеулердің аналитикалық теориясында беріледі. Айтатын болсақ келесі теорема дәлелденеді.
Теорема.
(6) - теңдеудің
 ерекше нүктесінің аймағында, жалпыланған дәрежелі қатар (13) түрінде кем дегенде бір дербес шешімі бар болу үшін, ол теңдеудің түрі келесідей болуы қажет:
ерекше нүктесінің аймағында, жалпыланған дәрежелі қатар (13) түрінде кем дегенде бір дербес шешімі бар болу үшін, ол теңдеудің түрі келесідей болуы қажет:
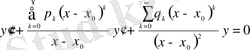 (14)
(14)
мұндағы
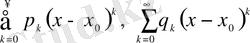 (15)
(15)
мағыналары жинақталатын дәрежелік қатарлар, сондай - ақ
 - коэффициенттері бір мезгілде нөлге тең емес немесе қарама - қарсы жағдайда
- коэффициенттері бір мезгілде нөлге тең емес немесе қарама - қарсы жағдайда
 нүктесі ерекше емес және
нүктесі ерекше емес және
 нүктесінің аймағында голоморфты екі сызықтық тәуелсіз екі шешімі бар. Сондай - ақ,
нүктесінің аймағында голоморфты екі сызықтық тәуелсіз екі шешімі бар. Сондай - ақ,
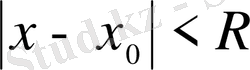 аймағында (14) - теңдеудің коэффициенттеріне енетін (15) қатарлар жинақталса, онда (13) шешіміне енетін (12) қатар кем дегенде сол
аймағында (14) - теңдеудің коэффициенттеріне енетін (15) қатарлар жинақталса, онда (13) шешіміне енетін (12) қатар кем дегенде сол
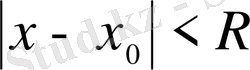 аймағында жинақталады.
аймағында жинақталады.
Бұл теореманың дәлелдеуі дифференциалдық теңдеулердің аналитикалық теориясында беріледі, онда ерекше
 нүктесі
регулярлы ерекше нүкте
деп аталады.
нүктесі
регулярлы ерекше нүкте
деп аталады.
Осы жерде біз тек
 көрсеткіші мен
көрсеткіші мен
 - коэффициенттерін анықтау әдістерін көрсетумен шектелеміз.
- коэффициенттерін анықтау әдістерін көрсетумен шектелеміз.
Жеңіл болу үшін x=0 деп алайық. Онда
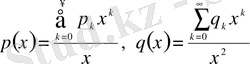 (16)
(16)
осыдан (14) - теңдеуі келесі түрге келеді:
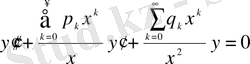 (17)
(17)
немесе
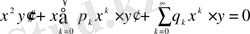 (18)
(18)
x - тің оң мәндерімен шектеле отырып, (18) - теңдеуінің шешімін келесі түрде іздейміз:
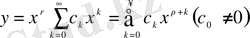 (19)
(19)
(19) - ды (18) - ге қойғанда, шығатыны:
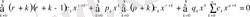 (20)
(20)
 - ға қысқартып және қатарларды қайта көбейту арқылы, алатынымыз:
- ға қысқартып және қатарларды қайта көбейту арқылы, алатынымыз:
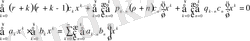 (21)
(21)
x - тің барлық дәрежелеріндегі коэффициенттерді нөлге теңестіреміз:
 (22)
(22)
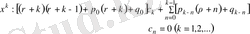 (23)
(23)
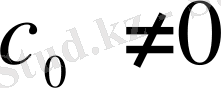 болғандықтан (22) -гі
болғандықтан (22) -гі
 - дің коэффициенті нөлге тең болуы қажет:
- дің коэффициенті нөлге тең болуы қажет:
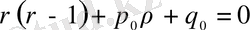 (24)
(24)
бұл теңдеу x=0 ерекше нүктесіндегі
анықтаушы теңдеу
деп аталады. Осы теңдеуден
 көрстекіштерінің мәні табылады.
көрстекіштерінің мәні табылады.
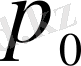 және
және
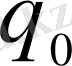 - анықтаушы теңдеудің коэффициенттері
- анықтаушы теңдеудің коэффициенттері
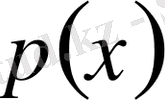 және
және
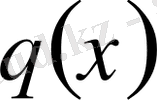 жіктемелеріндегі алымдарының бос мүшелері.
жіктемелеріндегі алымдарының бос мүшелері.
Ескерте кетейік, оларды анықтау үшін
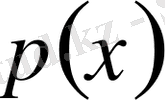 және
және
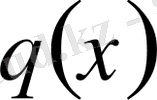 - ті жіктемей, келесі формулалар арқылы табуға болады:
- ті жіктемей, келесі формулалар арқылы табуға болады:
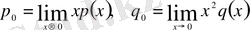 (25)
(25)
бұлардың дұрыстығын тікелей тексеру арқылы көз жеткізуге болады. Аналогиялық түрде (24) - анықтаушы теңдеудегі
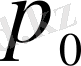 және
және
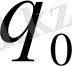 коэффициенттерін кез келген
коэффициенттерін кез келген
 нүктесінде анықтауға болады:
нүктесінде анықтауға болады:
 (26)
(26)
тағы бір ескерте кететін жәйт, (23) - формуладағы
 - ның коэффициенттерін анықтаушы теңдеудің сол жағындағы
- ның коэффициенттерін анықтаушы теңдеудің сол жағындағы
 - ны
- ны
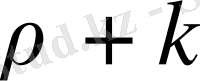 - ға алмастыру арқылы табуға болады.
- ға алмастыру арқылы табуға болады.
Анықтаушы теңдеудің түбірлерін
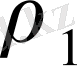 және
және
 деп белгілейік. Алыдмен
деп белгілейік. Алыдмен
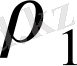 және
және
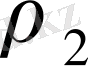 нақты және әртүрлі болғандағы жағдайды қарастырайық.
нақты және әртүрлі болғандағы жағдайды қарастырайық.
 деп есептейміз.
деп есептейміз.
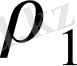 «бас» түбірге сәйкес жалпыланған қатар түрінде шешімнің әрдайым болатындығын көрсетейік.
«бас» түбірге сәйкес жалпыланған қатар түрінде шешімнің әрдайым болатындығын көрсетейік.
Расында, (23) - теңдігінде
 - нің орнына түбір
- нің орнына түбір
 - ді қойсақ,
- ді қойсақ,
 - нің коэффициенті келесідей болатындығын көреміз:
- нің коэффициенті келесідей болатындығын көреміз:
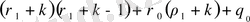 (27)
(27)
ал нөлден өзге немесе
 характеристикалық теңдеудің түбірі болмайды (себебі,
характеристикалық теңдеудің түбірі болмайды (себебі,
 болғандықтан
болғандықтан
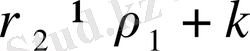 ) . Демек, (23) - формуладан біз
) . Демек, (23) - формуладан біз
 - нің барлық коэффициенттерін біртіндеп таба аламыз.
- нің барлық коэффициенттерін біртіндеп таба аламыз.
 - екенін табамыз, және де
- екенін табамыз, және де
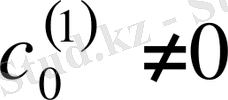 - кез келген сан.
- кез келген сан.
(19) - формуладағы
 және
және
 - нің орнына
- нің орнына
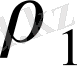 және
және
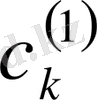 - ді қойсақ, алатынымыз:
- ді қойсақ, алатынымыз:
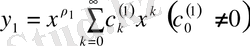 (28)
(28)
оң жағындағы дәрежелік қатар кем дегенде
 аймағында жинақталатынын дәлелдеуге болады, сондықтан (28) - формуласы (18) - теңдеудің шешімі.
аймағында жинақталатынын дәлелдеуге болады, сондықтан (28) - формуласы (18) - теңдеудің шешімі.
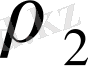 түбіріне сәйкес келетін жалпыланған дәрежелік қатар түріндегі екінші дербес шешімін анықтауда, анықтаушы теңдеу шешімдерінің айырмасы, яғни
түбіріне сәйкес келетін жалпыланған дәрежелік қатар түріндегі екінші дербес шешімін анықтауда, анықтаушы теңдеу шешімдерінің айырмасы, яғни
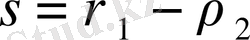 маңызды орын алады.
маңызды орын алады.
Егер
 бүтін оң сан болмаса, онда жалпыланған дәрежелік қатар
бүтін оң сан болмаса, онда жалпыланған дәрежелік қатар
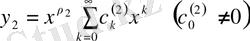 (29)
(29)
түріндегі
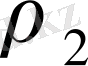 түбіріне сәйкес шешімі бар болады. Нақтысында, осы шешімді іздеу барысында біз
түбіріне сәйкес шешімі бар болады. Нақтысында, осы шешімді іздеу барысында біз
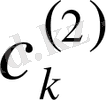 - нің коэффициенті
- нің коэффициенті
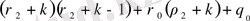 (30)
(30)
нөлден өзге екендігін анықтаймыз немесе
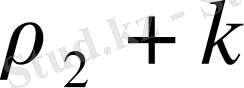 анықтаушы теңдеудің түбірі болмайды. Сондықтан барлық
анықтаушы теңдеудің түбірі болмайды. Сондықтан барлық
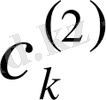 анықталады және кез келген
анықталады және кез келген
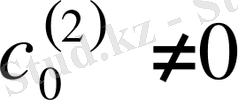 .
.
Егер
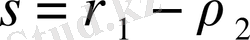 оң бүтін сан болса, жалпы жағдайда (29) формула түріндегі шешімнің бар болуына кепілідік берілмейді, не болмаса сол жағдайда
оң бүтін сан болса, жалпы жағдайда (29) формула түріндегі шешімнің бар болуына кепілідік берілмейді, не болмаса сол жағдайда
 - нің коэффициенті нөлге тең.
- нің коэффициенті нөлге тең.
Егер
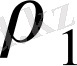 және
және
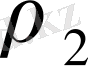 - түбірлері әртүрлі, бірақ комплекс сан
- түбірлері әртүрлі, бірақ комплекс сан
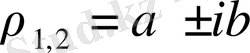 болса, онда әр бір түбірге сәйкес жалпыланған дәрежелік қатарлар түрінде бар болады.
болса, онда әр бір түбірге сәйкес жалпыланған дәрежелік қатарлар түрінде бар болады.
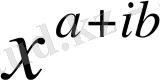 көбейткіші болып
көбейткіші болып
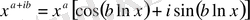 (31)
(31)
өрнегі табылады.
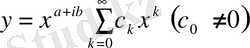 (32)
(32)
(мұндағы
 - нің коэффициенттері комплекс сандар)
- нің коэффициенттері комплекс сандар)
Комплекс шешімде нақты және жалған бөліктерін айыру арқылы, (18) - теңдеудің екі нақты сызықтық тәуелсіз дербес шешімдерін табамыз.
Анықтаушы теңдеудің
 еселі түбірлері болған жағдайда жалпыланған дәрежелік қатар түрінде бір ғана шешім бар болады. s оң бүтін
еселі түбірлері болған жағдайда жалпыланған дәрежелік қатар түрінде бір ғана шешім бар болады. s оң бүтін
немесе нөл болғандағы екінші дербес шешімнің аналитикалық түрін анықтайық. Ол үшін
 - ні
- ні
 мен p(x) арқылы өрнектейтін формуланы қолданайық:
мен p(x) арқылы өрнектейтін формуланы қолданайық:
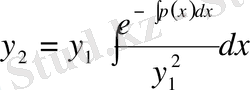 (33)
(33)
мұндағы
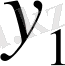 - ді жалпыланған дәрежелік қатар түріндегі аналитикалық берілуімен алмастырайық:
- ді жалпыланған дәрежелік қатар түріндегі аналитикалық берілуімен алмастырайық:
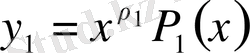 (34)
(34)
мұндағы
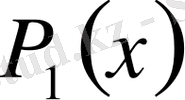 - бос мүшесі нолге тең емес Тэйлер қатары. Бос мүшесі нолге тең емес Тэйлер қатарын
- бос мүшесі нолге тең емес Тэйлер қатары. Бос мүшесі нолге тең емес Тэйлер қатарын
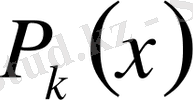 - деп белгілейтін боламыз.
- деп белгілейтін боламыз.
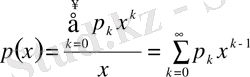 (35)
(35)
болғандықтан
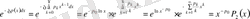 (36)
(36)
сондықтан
 (37)
(37)
(24) - анықтаушы теңдеудің түбірлерін
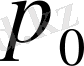 арқылы өрнектейік:
арқылы өрнектейік:
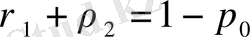 , осыдан
, осыдан
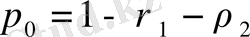 (38)
(38)
яғни
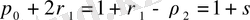 (39)
(39)
(37) - ге қою арқылы, алатынымыз:
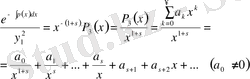 (40)
(40)
Бұл жерде біз s тек оң бүтін сан деп болжаймыз, олай болмаса біз
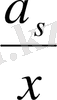 бос мүшесін шығара алмаймыз. Симметрия үшін келесі белгілеулерді енгізейік:
бос мүшесін шығара алмаймыз. Симметрия үшін келесі белгілеулерді енгізейік:
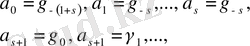 (41)
(41)
(40) - ты келесі түрде көшіріп жазайық
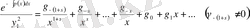 (42)
(42)
(40) - ты (33) формуласына қойып және
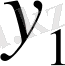 - мәнін (34) - гімен алмастырып,
- мәнін (34) - гімен алмастырып,
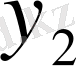 - үшін келесі өрнекті аламыз:
- үшін келесі өрнекті аламыз:
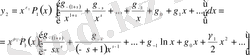 (43)
(43)
Құрамына lnx кіретін мүшені бөлек қойып, ал қалған мүшелерден
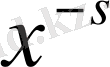 - ті жақша сыртына шығарайық, алатынымыз:
- ті жақша сыртына шығарайық, алатынымыз:
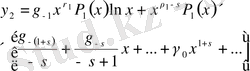 (44)
(44)
 болғандықтан
болғандықтан
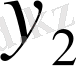 қорытынды түрі келесідей болады:
қорытынды түрі келесідей болады:
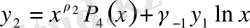 (45)
(45)
Осыдан щығатыны, қарастырылып отырған (s - теріс емес бүтін сан) жағдайда екінші дербес шешімнің құрамына тек жалпыланған дәрежелік қатар ғана емес lnx көбейткіші кіреді. Ол нөлден өзге болуы мүмкін
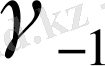 коэффициентінің шамасына тәуелді, және де егер s=0 болса, яғни
коэффициентінің шамасына тәуелді, және де егер s=0 болса, яғни
 , онда
, онда
 алдын ала нөлден өзге, не болмаса осы жағдайда нөлге тең емес
алдын ала нөлден өзге, не болмаса осы жағдайда нөлге тең емес
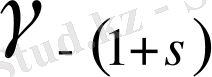 коэффициенті
коэффициенті
 - ге айналады. Сондықтан
- ге айналады. Сондықтан
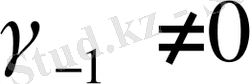 . Демек, анықтаушы теңдеудің түбірлері еселі болған жағдайда екінші дербес шешімнің түрі келесідей болады:
. Демек, анықтаушы теңдеудің түбірлері еселі болған жағдайда екінші дербес шешімнің түрі келесідей болады:
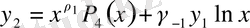 (46)
(46)
мұндағы
 .
.
Ескерте кетейік, жалпыланған дәрежелік қатарлар немесе оданда жалпы (45) қатарлар түріндегі шешімдерді іздегенде, егер шешімге кіретін дәрежелік қатарлар үзілісті болса немесе белгілі элементар функциялардың Тэйлор қатарына жіктелуі болса, дәрежелік қатарлар арқылы интегралдаудағы секілді, кей кезде элементар функциялар түріндегі шешімдерді анықтауымыз мүмкін.
Мысал 1. Эйлер теңдеуін қарастырайық
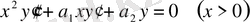 (47)
(47)
x=0 нүктесі регулярлы ерекше нүкте болып табылады, сондықтан (47) теңдеуін
 (48)
(48)
түрінде жазуға болады. Осы ерекше нүктеде анықтаушы теңдеуі
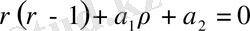 (49)
(49)
болады.
Алдымен
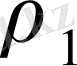 мен
мен
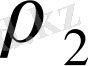 теңдеудің түбірлерін нақты және әр түрлі деп болжайық. «Бас» түбірге сәйкес шешімді құрайық:
теңдеудің түбірлерін нақты және әр түрлі деп болжайық. «Бас» түбірге сәйкес шешімді құрайық:
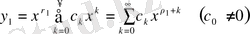 (50)
(50)
(50) - ді (47) - ге қойып және
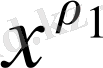 - ге қысқартсақ, шығады:
- ге қысқартсақ, шығады:
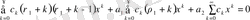 (51)
(51)
x - тің барлық дәрежелеріндегі коэффициенттерді нөлге теңестіреміз:
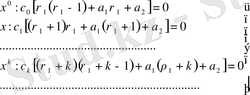 (52)
(52)
екіншіден бастап барлық тік жақшалар нөлден өзге болғандықтан:
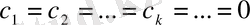 (53)
(53)
 - коэффициенті нөлден өзге кез келген сан.
- коэффициенті нөлден өзге кез келген сан.
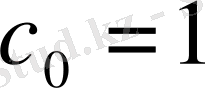 деп болжап, ізделінді дербес шешімді табамыз:
деп болжап, ізделінді дербес шешімді табамыз:
 (54)
(54)
Екінші шешімді (33) - і формула арқылы табамыз. Шығатыны:
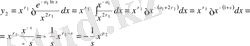 (55)
(55)
s - оң бүтін сан болатындығына не болмайтындығына тәуелсіз екінші дербес шешімді
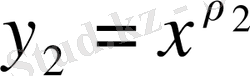 (56)
(56)
деп алуға болады. Барлық жағдайда екінші шешімнің құрамында lnx болмайды, себебі
 және
және
 нақты болғандықтан, (54), (56) - шешімдері де нақты болады.
нақты болғандықтан, (54), (56) - шешімдері де нақты болады.
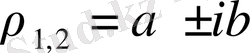 комплекс түбірлерге екі нақты (сызықты тәуелсіз) түбірлер сәйкес келеді, олар
комплекс түбірлерге екі нақты (сызықты тәуелсіз) түбірлер сәйкес келеді, олар
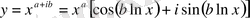 (57)
(57)
комплекс шешімінен нақты және жалған бөліктерін айыру арқылы табылады:
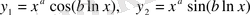 (58)
(58)
Егер
 болса, онда
болса, онда
 .
.
 - ні табу үшін (55) - ші формуланы қолданып табамыз, тек ескерте кету керек, біздің жағдайда
- ні табу үшін (55) - ші формуланы қолданып табамыз, тек ескерте кету керек, біздің жағдайда
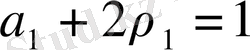 . Сонда:
. Сонда:
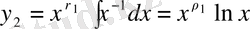 (59)
(59)
Болжағандай
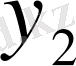 - нің құрамында lnx бар.
- нің құрамында lnx бар.
Мысалы 2.
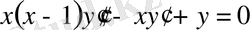 (60)
(60)
теңдеуінің жалпыланған дәрежелік қатарлар арқылы x=0 ерекше нүктесінің аймағында екі сызықтық тәуелсіз шешімдерін табу керек.
Алдымен x=0 нүктесі регулярлы ерекше нүкте екендігіне көз жеткізейік.
Осы теңдеудің екі жағын
 - тің алдында тұрған коэффициентке бөлсек, шығады:
- тің алдында тұрған коэффициентке бөлсек, шығады:
 (61)
(61)
 - тің коэффициенті x=0 нүктесінің маңайында голоморфты немесе
- тің коэффициенті x=0 нүктесінің маңайында голоморфты немесе
 (62)
(62)
ал y - тің коэффициентін келесі түрде көрсетейік:
 (63)
(63)
(62) және (63) жіктеулерін (16) жіктеулерімен салыстырсақ x=0 регулярлы ерекше нүкте екендігі анықталады.
x=0 ерекше нүктесінде анықтаушы теңдеу
 (64)
(64)
болады. Оның екі
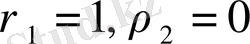 оң бүтін түбірлері бар.
оң бүтін түбірлері бар.
 түбіріне
түбіріне
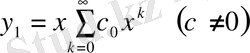 (65)
(65)
- шешімі сәйкес келеді.
Мұндағы оң жағындағы қатар кемінде
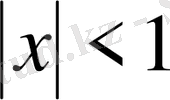 аймағында жинақталады.
аймағында жинақталады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz