ТРИГОНОМЕТРИЯЛЫҚ ЖҮЙЕ БОЙЫНША ҚҰРЫЛҒАН ФУРЬЕ ҚАТАРЛАРЫНЫҢ КЕЙБІР ҚАСИЕТТЕРІ

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 39 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Ш.Уәлиханов АТЫНДАҒЫ КӨКшЕТАУ МЕМЛЕКЕТТІК

УНИВЕРСИТЕТі

ФИЗИКА-МАТЕМАТИКА ФАКУЛЬТЕТІ

Математика ЖӘНЕ ОҚЫТУ ӘДІСТЕМЕСІ кафедрасы

Тригонометриялық жүйе бойынша құрылған Фурье қатарларының кейбір
қасиеттері.

ДИПЛОМДЫҚ ЖҰМЫС

МАМАНДЫҒЫ: МАТЕМАТИКА

Көкшетау

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Ш.Уәлиханов АТЫНДАҒЫ КӨКШЕТАУ МЕМЛЕКЕТТІК

УНИВЕРСИТЕТі

ФИЗИКА-МАТЕМАТИКА ФАКУЛЬТЕТІ

Математика ЖӘНЕ ОҚЫТУ ӘДІСТЕМЕСІ кафедрасы

Қорғауға жіберілді

Кафедра меңгерушісі
профессор, т.ғ.д. Қ.Ж.Байшагиров.
“ ” _ _ _ _ _ _ _ _ _ _ 200 г

ДИПЛОМДЫҚ ЖҰМЫС

Тригонометриялық жүйе бойынша құрылған Фурье қатарларының кейбір
қасиеттері.

МАМАНДЫҒЫ: МАТЕМАТИКА

Студент
Ғылыми жетекшісі
ф.-м.ғ.к., доцент
Жантілесов Ж.Х.

Көкшетау

Кіріспе

Тригонометриялық Фурье қатарларының теориясы ең алғаш рет 1807 жылы
Ж.Фурьенің жылуөткізгіштер есептерін шешу барысында пайда болды. Ол
алғашында функцияны тек (0, 2) интервалында ғана қарастырды.
Фурье өз шығармасында функцияның тригонометриялық жіктелуі
дұрыстығын дәлелдемек болып әрекет жасайды, алайда оның келтірген
талқылаулары аналитикалық дәлдігі жағынан мүлтіксіз емес еді, бірақ оның
геометриялық формаға келтірген негізгі идеясы дұрыс болатын-ды. Бұдан кейін
басқа авторлар да, соның ішінде Коши де, талаптанып көрді, бірақ бұларға
қарсы пікір айтушылар да табылды.
Фурье айтқан ұйғарымның бірінші болып шын мәніндегі мүлтіксіз
дәлелдемесін келтірген Дирихле (1829 ж.) еді; ол дәлелдемесінде шындығында
Фурьенің идеясын пайдаланады. Алайда осыған қатысты еңбегінің аталуында
Дирихле кез келген функцияны ескерткенімен, іс жүзінде қарастыратын
функциялар класын дәлдеп шектейді: бұлар аралықта анықталған және
шектеулі, үзінді-үздіксіз және үзінді-монотонды функциялар. Егер f(x)
функциясы осы талаптарды қанағаттандыратын болса, онда Фурье формулалары
бойынша ол функция үшін құрастырылған тригонометриялық қатар болғанда

қосындысына жинақталады да, ал болғанда

қосындысына жинақталады.
1834—1835 жылдары Лобачевский де жіктеу теоремасының дәлелдемесін
көрсетті, оның функцияға қойған шарттары Дирихле көрсеткеннен өзгеше еді.
Иә, Лобачевский тек саны шектеулі секірістер мен функцияның өзі не оның
туындысы сол немесе оң жағынан -ке айналатын нүктелерден басқа
нүктелерде функцияны жалпы дифференциалданатын деп алады, мұнымен бірге
функция интегралданатын болып қала беруі тиіс — меншікті не меншікті емес
мағынада. Дирихле мен Лобачевский екеуінің қойған шарттары өз ара
қабыспайды.
Бертін келе басқа авторлар Фурье қатарының алғашқы функцияға
жинақты болуының анағұрлым жалпылау бірқатар жеткіліктілік белгілерін
тағайындап берді.
Тригонометриялық қатарлар теориясын дамытуда Риманның белгілі
диссертациясы маңызды орын алады (1854 ж., ал 1867 ж. жарық көрді). Ол —
мәселенің тарихы жөніндегі очеркпен басталады. Бұдан кейін автор анықталған
интеграл ұғымын айқындай түседі және оның болу шартын тағайындайды. Осының
өзі Фурье қатарларының қолданылу облысын кеңейтті, мысалы, Дирихле
теоремасында функцияның үздіксіздігі жөнінде ешқандай ұйғарым жасаудың
қажет еместігі анықталды. Алайда еңбектің негізгі мазмұны тригонометриялық
қатарлардың жалпы түрін

(1)
карастырумен және периоды кез келген функцияны бұған ұқсас қатар
түрінде көрсету үшін қажетті шарттарды анықтаумен байланысты еді.
Жоғарыдағы (1) түріндегі қатарды Риман

қатарымен салыстырады. Бұл қатар жоғарыдағы қатарды мүшелеп екі қайтара
интегралдағанда формальды түрде шығады. Ал және шарттары
орындалғанда, соңғы қатар бүкіл -пен -ке дейінгі аралықта бір
қалыпты жинақталады және ол аралықта үзіліссіз F (х) функциясын анықтайды.
F (х) функциясының қасиеттеріне және оның f (x) функциясымен байланысына
еңбектің соңғы бөлімі арналған. Риман диссертациясына оның (1) қатарды
зерттеу әдісін пайдаланған басқа авторлардың бірқатар еңбектері және тапқан
нәтижелері жақын келеді.
Ең алдымен функцияның тригонометриялық жіктеуінің бірден-бірлігі
жөніндегі мәселе туды: өйткені осындай жіктеудің коэффициенттерін беретін
Эйлер — Фурье формулалары қатарды мүшелеп интегралдау жолымен табылды, ал
өткен ғасырдың екінші жартысында бұл сияқты тәсілді сөзсіз қолдану мүмкін
еместігі жете түсінілді. Бұл мәселені алғаш рет қойған 1870 ж. Гейне еді,
алайда оның толық шешімін сол тұста-ақ Қантор көрсеткенді, ол мынадай жалпы
теореманы дәлелдеді: егер f (х) фунциясын аралықта (1) түріндегі
қатарға жіктеу жалпы мүмкін болса, ондай жіктеу бірден-бір ғана.
Көрсетілген аралықта қатардың қосындысы, тіпті оның жинақтылығы
жөнінде де ештеңе белгісіз болатын ерекше нүктелер бар болғанның өзінде де
жіктеудің бірден-бірлігі сақталып қала береді (тек қана осындай ерекше
нүктелер жиыны шектеусіз болса, оны қандай бір шарттармен шектеуге тура
келеді).
Интегралданатын f(x) функциясының бірден-бір жіктеуінің (егер ол мүмкін
дейтін болсақ) коэффициенттері қандай болмақ? Олар қашан да сол Фурье
коэффициенттері болмақ па? Әрине, бұл сұрақты Эйлер — Фурье
формулаларындағы интегралдардың жалпы мағынасы болатын функциялар жөнінде
қойған дұрыс болар еді. Бір тамашасы, ол сұраққа мақұлдап жауап беруге
болады екен, бұны алдымен 1872 ж. үздіксіз функциялар үшін Асколи, ал
меншікті мағынасында интегралданатын функциялар үшін дю Буа-Реймон
тағайындады. Бертін келе бұл нәтиже анағұрлым жалпылау мағынада
интегралданатын функцияларға да қолданылатын болды. Зерттеушілердің
фунцияларды Фурье қатарларына жіктеу мәселесіне ерекше назар аударғандығы
осы еңбектермен ақталғандай болды.
Енді тағы бір мәселеге тоқтап өтейік. Дирихле периодты әрбір үздіксіз
функция Фурье қатарына жіктеледі деп нық сенді, алайда мұны ол дәлелдей
алмады, Бұл пікірді, сірә, басқа математиктер де қолдаған сияқты. Алайда дю
Буа-Реймон Дирихле ұйғарымының дұрыстығын дәлелдемек болып бірқатар
әрекеттенгеннен кейін, 1876 жылы мысалмен оны теріске шығарды, бұл үшін ол
мейлінше кішкене аралықтағы шектеусіз көп нүктелер жиынында Фурье қатары
жинақты болмайтын үздіксіз функция құрды.
Ең алдымен, бүл теориямен функция ұғымының өзі тығыз байланысты. Эйлер
мен Д. Бернуллидің кез келген функцияны тригонометриялық қатарға жіктеу
женіндегі айтысының кейбір ағат және теріс пікірлерді жою үшін көп себі
тиді, кейін бүл Фурье еңбектерінде қорытындыланды. Функцияға қазір беріліп
жүрген жалпы анықтаманы Лобачевский мен Дирихленің тригонометриялық
қатарлар жөніндегі зерттеулерінен біздің тауып отырғанымыз кездейсоқ емес!
Фурье қатарларының теориясының қажеттігімен байланысты, Римананның
анықталған интеграл ұғымын айқындап, жалпылады. Кантор шектеусіз жиындар
теориясын жасағанда алғашқы қадамын тригонометриялық жіктеудің бірден-
бірлігі жөніндегі мәселе тұрғысынан жасады. Қазіргі кездегі жинақты емес
қатарлардың жалпыланған қосындылау теориясы тригонометриялық қатарларды
қосындылау жөніндегі Пуассон зерттеулерінен басталады. Тіпті егер
анализдің қайсы бір нәзік ұғымдары (мысалы, сандық қатардың абсолют және
абсолют емес жинақтылығы, функционалдық қатардың бір қалыпты және бір
қалыпты емес жинақтылығы) тригонометриялық қатарлар теориясымен байланыссыз
пайда болса да, осы қатарларға бірден қолданылып кетті, мұның өзі бір
олардың мән-мағынасын байқау үшін қажет болғандай.
Тригонометриялық қатарлар математикалық физикада тікелей қолданылып жүр
(ішектің тербелісі жөніндегі есеп) және де техниканың басқа салаларында да
қолданылып жүр. Ал Фурье жалпыланған қатарлары, яғни ортогональ
функциялардың әр түрлі басқа системалары бойынша жіктеулері аса кең
қолданылып жүр; бұлар үшін Фурье қатарларының теориясымен тығыз ұштасып
жататын тригонометриялық жіктеулер мен теория үлгі деп саналады.
Дипломдық жұмыс екі тараудан, қорытындыдан және қолданылған әдебиеттерт
тізімінен тұрады.

Дипломдық жұмыстың мақсаты функцияларды тригонометриялық жүйе бойынша
Фурье қатарларына жіктеп, олардың қасиеттерін, атап айтсақ, жинақталу
шарттарын зерттеу.
Бірінші тарауда периоды болатын функциялардың тригонометриялық
жүйе бойынша құрылған Фурье қатарларының қасиеттері, Фурье
коэффициентерінің формулалары және осы жүйе бойынша функцияларды Фурье
қатарларына жіктеу мысалдары берілген. Осы тарауда Фурье қатарының негізі
болып саналатын Риман ұстамы дәлелденген.
Екінші тарауда f функциясының тригонометриялық Фурье қатары x
нүктесінде f(x) мәніне жинақталуы щарттары және Фурье қатарының үзіліс
және үзіліссіздік нүктелеріндегі жинақталуының жеткілікті шарттары, Дини
және Липшиц теоремалары берілген.

1-тарау. ТРИГОНОМЕТРИЯЛЫҚ ЖҮЙЕ БОЙЫНША ҚҰРЫЛҒАН ФУРЬЕ ҚАТАРЛАРЫНЫҢ
ҚАСИЕТТЕРІ.

§1. Периодты шамалар және гармониялық анализ.

Ғылым мен техникада периодты құбылыстар, мысалы, белгілі бір
уақыт аралығынан, Т (бұл период деп аталады) кейін де сол бұрынғы күйіне
кайыра түсіп отыратын құбылыстар өте жиі ұшырасады. Бұған мысал ретінде бу
машинасының әбден қалыптасқан қозғалысын айтуға болады; бұл толық айналым
уақыты өткеннен кейін, машина қайтадан өзінің бастапқы жағдайына келеді,
сондай-ақ осы айтылғанға айнымалы ток құбылысы т. б. мысал бола алады.
Қарастырылып отырған периодты құбылыстармен байланысты келетін әр түрлі
шамалар период Т уакыт өткеннен кейін, өздерінің бұрынғы мәндеріне қайыра
оралады да, сөйтіп, уақыттың периодты функциялары болып табылатын болады,
бұларды мынадай теңдікпен сипаттап көрсетуге болады:

Мысалы, айнымалы токтың күші мен кернеуі не болмаса—бу машинасын
мысалға алғанда — крейцкопфтың жолы, жылдамдығы және үдеуі, бу қысымы,
кривошип шабағына түсірілген жанама күш т. с. с. осындай функциялар болып
табылмақ.
Периодты функциялардың ішіндегі ең қарапайымы синусоидалық шама
болмақ: , мұнда — жиілік, оның период -мен байланысы
мынадай:

(1)
Осы сияқты карапайым периодты функциялардан бұдан гөрі күрделірек
функцияны құруға да болады. Ең алдымен мынаны ескерген жөн: құрастырушы
синусоидалық шамалардың, жиіліктері әр түрлі болуы шарт, олай болмағанда
жиілігі бірдей синусоидалык шамаларды қосқанда басқа шама шықпай, қайтадан
жиілігі сол бұрынғыдай синусоидалық шама шығады. Ал керісінше
жағдайда, егер мынадай бірнеше шамаларды қосатын болсақ:

бұлардың жиіліктері тұрақты болмағанда,болады да, бұлар ішіндегі ең
кішісі -ға еселі болады және периодтары

болатын периодты функция шығады.
Мысал үшін синусоидалық үш шаманы қосып көрсетейік (1-сурет):

бұл функцияның графигі сипаты жағынан алғанда синусоидадан әлдеқайда өзгеше
шамалардан құралған шектеусіз

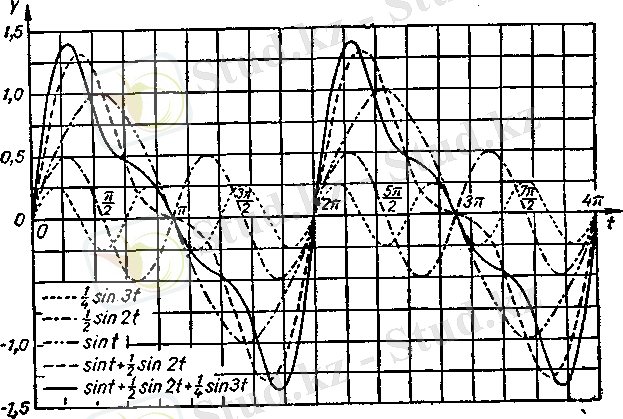
1-сурет.
қатардың қосындысын алатын болсақ, олардың графигіндегі айырмашылық күшейе
түседі.
Енді бұған керісінше сұрақты қою орынды-ақ: периоды Т болатын
берілген периодты функцияны синусоидалық шамалардың шектеулі, тіпті
болмаса шектеусіз жиынының қосындысы түрінде өрнектеп көрсетуге бола ма?
Функциялардың айтарлықтай көлемді класына қатысты айтқанда бұл сұраққа,
егер осы шамалардың бүкіл шектеусіз тізбегін қамтитын болсақ,
қанағаттанарлық жауап беруге болатынын кейін байқаймыз.
Осы класс функцияларын тригонометриялық қатарға жіктеуге болады:
(3)
мұндағы осындай функциялардың әрқайсысы үшін ерекше мәнге ие болатын
тұрақты шамалар, ал жиілік (1) формуламен анықталады.
Геометрия тұрғысынан түсіндіргенде, периодты функцияның графигі
бірқатар синусоидаларды бір-біріне қосқаннан немесе азайтқаннан шығады.
Егерде әрбір синусоидалық шаманы гармониялық тербелмелі қозғалысты
білдіреді деп механикалық түрде түсіндіретін болсақ, онда
функциясымен сипатталатын күрделі тербеліс жекелеген гармониялық
тербелістерге жіктеледі деуге де болады. Осымен байланысты (3) жіктеудің
құрамына енетін жекелеген синусоидалық шамаларды функциясының
гармониялық құраушылары деп не оларды жай ғана гармоникалар деп атайды. Ал
периодты функцияның гармоникаларға ажырау үрдісінің өзі гармониялық анализ
делінеді.
Егер тәуелсіз айнымалы деп

алсақ, онда -ке тәуелді функция шығады:

бүл да периодты функция, оның периоды .
Сонымен, (3) түрдегі жіктеуді жаңадан енгізілген х аргументі арқылы

(4)
түрінде жазамыз.
Бұл қатардың мүшелеріндегі қосындының синусын формула бойынша ашып
жазып және былай деп алсақ:

тригонометриялық жіктеудің ақырғы формасын шығарып аламыз:
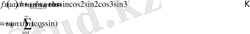(5)
Мұнда х бұрышына тәуелді, периоды функция -ке еселі
бұрыштардың синустары мен косинустары бойынша жіктелген болып табылады. Біз
мәселені периодты тербелмелі құбылыстардан және бұлармен байланысты
шамалардан бастай отырып, функцияны тригонометриялық қатарға жіктеу
мәселесіне келдік.
Мынаны атап өту орынды: қазірдің өзінде-ақ, бұған ұқсас жіктеулер
белгілібір шектеулі аралықта берілген және ешбір тербелмелі құбылыстың
нәтижесі емес функцияларды зерттеп тексергенде пайдалы болып шығатын жағдай
жиі ұшырайды.

§2. Синус және косинус функцияларының қасиеттері

Теорема. Кез келген 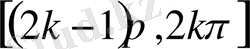сегментінде сosх функциясы +1-ден
-1-ге шейін кемиді; кез келген сегментінде сosх функциясы -1-ден 1-ге
дейін өседі.
Дәлелдеу: Бұл теореманы тек [0, π] және [-π, 0] екі сегменттері үшін
дәлелдесек жеткілікті.
сosх функциясының [0, π] сегментінде 1-ден -1-ге шейін кемитінін
дәлелдейік. Ол үшін мына үш тұжырымды дәлелдеу қажет.
10. сosх функциясы [0, π] сегментінде кемиді.
20. Сегменттің шекаралық нүктелерінде косинустың мәндері +1 мен
-1-ге тең, яғни cos0=1, cosπ=-1.
30. сosх функциясы [0, π] сегментінде -1 мен 1 аралығында кейбір
нүктелерінде m мәнін қабылдайды. Шынында да [0, π] сегментінде бір ғана
доға бар болады, мұнда косинус мынаған тең: cos c =m.
10 тұжырымды дәлелдеу ғана қалды. Айталық, 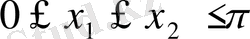. Мұнда х1 және х2
[0, π] сегментінен алынған аргументтің мәндері. cos x2 – cos x1 айырымын
құрамыз, оны мына көбейтінді түрінде жазамыз:

(*)
теңсіздігінен және шығады. Демек,

және

функциялары берілген аралықта анықталғандықтан, олардың көбейтіндісі бар
болып, қашанда оң болады. Себебі,
cos x2 – cos x10 және cos x2 cos x1.
Сонымен, аргументтің үлкен мәніне косинустың кіші мәні сәйкес келеді,
демек, берілген сегментте сosх функциясы кемиді.
сosх функциясы [-π, 0] сегментінде -1-ден 1-ге шейін өседі.
10. Егер болса, онда

және
.
Осыдан кейін (*) теңдеуінен теріс анықталған, себебі,
cos x2 – cos x10 және . cos x2 cos x1, демек, берілген сегментте сosх
функциясы өседі.
20. cos(-π) =-1, cos 0 =1 екені белгілі.
30. Егер 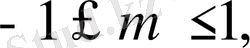онда cos c =m.
Теорема. Кез келген 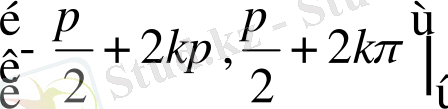сегментінде sinx функциясы -1-ден 1-ге
шейін өседі; кез келген сегментінде 1-ден -1-ге дейін sin x
функциясы кемиді. Оның дәлелдеу жолы сos х функциясының дәлелдеу жолымен
ұқсас.
y=a cos x + b (немесе a sin x + b) функциясы ең үлкен және ең кіші
мәнге ие болады, яғни және .
функциясының ең үлкен және ең кіші мәні мынаған тең: және

Осыдан мына теңсіздік шығады:
Теорема. Тригонометриялық функциялар анықталу облыстарында үзіліссіз.
10 Синус және косинус периодты функциялар, олардың периоды -ге тең:
Sin( x +)= sinx
Сos(х+)= сosх.
20 Синус тақ функция, ал косинус жұп функция.
Синус функциясының графигі координатаның бас нүктесіне қатысты симметриялы
болады.
30 Косинус функциясының графигі ординатаға қатысты симметриялы болады.
40 аралығында синус және косинус функциялары үшін келесі интегралдық
теңдіктер орындалады:

.

§ 3. Тригонометриялық жүйе бойынша құрылған Фурье қатарларының
коэффициенттерін есептеу.

Периоды -ға тең f(x) функциясы үшін

тригонометриялық жіктеудің мүмкін болатындығын тағайындау үшін,
коэффициенттердің нақтылы жиынтығын аламыз.
Айталық, f(x) функциясы аралығында интегралданып және
жоғарыда айтылғандай, тригонометриялық функциялардың қосындысы түрінде
өрнектелсін, яғни
Осы өрнекті, жоғарыда берілген синус және косинус функцияларының
қасиеттерін пайдаланып, аралығында мүшелеп интегралдаймыз, сонда:

Сондықтан қосынды таңбасының астындағы барлық мүшелер нөлге тең болады.

Коэффициент ат шамасын білу үшін, (5) теңдіктің екі жақ бөлігін де -
ке көбейтіп, тағы да сол аралықта қайтадан интегралдаймыз: ;

Оң жақтағы бірінші қосылғыш нөлге тең болады. Әрі қарай, болғанда
интеграл астындағы тригонометриялық функциялардың көбейтінділерін
қосылғыштарға жіктеп, мүшелеп интегралдаймыз.
(8)
(9)
және, ақырында,
(10)
Сонымен, көбейткіші сол коэффициент ат болатын интегралдан өзге қосынды
таңбасының астындағы барлық интегралдар нөлге айналады. Осыдан кейін бұл
коэффициент :
(11)
Егер (5) жіктеуді алдын ала sinтх-ке осылайша көбейтіп және мү-
шелеп интегралдасақ, синустың алдында тұрған коэффициенттерді
анықтаймыз:
(12)
Бұл жерде (6) мен (8) қатыстармен қатар алдыңғы параграфта берілген

(13)
және болса:

(14)
Синус пен косинус функцияларының қасиеттерін ескереміз.
(7), (11) және (12) формулалар Фурье формулалары деп аталады. Бұл
формулалар бойынша есептеп шығарылған коэффициенттер берілген функцияның
Фурье коэффициенттері деп, ал олардың көмегімен құрылған тригонометриялық

қатар функцияның Фурье қатары деп аталады.
Біз басында тригонометриялық (5) қатар орындалады деп ұйғарған
болатынбыз, ендеше функция мен қатардың арасындағы теңдік үнемі орындала
ма деген сұрақ туады. Біз қатарды мүшелеп интегралдауды қайыра қолдандық,
ал бұл амал әр уақыт рұқсат етіле бермейді. Оны қолданудың жеткілікті
шарты қатардың бір қалыпты жинақтылығы болмақ. Сондықтан тиянақты
тағайындалған деп тек мына жағдай саналады:
Егер f(x) функциясы бірқалыпты жинақталатын тригонометриялық (5)
қатарға жіктелетін болса, онда бұл қатар функцияның Фурье қатары болуы
қажетті.
Егерде қатардың жинақтылығын бір қалыпты деп ұйғармасақ, онда
функцияның Фурье қатарына жіктеле алатындығын да дәлелдеп беру қиын.
Жасалған байымдауларды тек берілген функцияның тригонометриялық жіктелуін
іздестіргенде, оны Фурье қатарына жіктеуден бастау үшін ғана байқап көру
деп түсіну керек.
Әзірге дейін бұлар белгісіз, біз тек берілген f(x) функциясының
Фурье қатарын формальды түрде қарастыра аламыз, алайда ол жөңінде тек f(x)
функциясынан шыққан дегеннен басқа ештеңе айта алмаймыз.
Қатардың функциясымен осы б а й л а н ы с ы н әдетте теңдік
таңбасын қолданбай, былай белгілейді;
~ (5а)
§ 4. Дирихле интегралы.

Айталық, f(x) функциясы үзіліссіз, не санаулы нүктелерде үзілісті және
периоды 2 болсын. Оның Фурье коэффициенттері
(m = 0, 1, 2, ...)

(m = 1, 2, 3, ...)
Формулалары арқылы есептелетіндігін жоғарыда көрсеттік.
Берілген f(x) функциясының тригонометриялық жүйе бойынша құрылған Фурье
қатарын құрайық:
~ (2)
Біз бұл жерде ат үшін т = 0 болғанда, оның бос мүшесін түрінде
жаздық.
Ескерту. Егер F(u) функциясы кез келген шектеулі аралықта үзінді-үздіксіз
және оның периоды 2 болса,

теңдігі орындалғандықтан,

интегралының шамасы ұзындығы 2 аралықта а-ға тәуелсіз болады.
Шынында да, F функциясының үздіссіз жағдайын ғана алып. мынаны табамыз:

Егер соңғы интегралда деп ауыстырсақ, онда ол мына интегралға келеді:

мұның алдыңғы интегралдан айырмашылығы тек таңбасында ғана.
Сонымен, қарастырылып отырған интеграл мына интегралға тең болып
шықты:

бұған енбей отыр. Бұл табылған нәтижені кез келген үзінді-үздіксіз
функцияға да қолдануға болады .
Бұл ескертпені біз ілгеріде пайдаланатын боламыз. Дербес жағдайда,
Фурье коэффициенттерін анықтайтын (1) формулаларда интегралдарды ұзындығы
2 аралық бойынша алуға болады; мысалы, былай жазуға болар еді:

(la)
Қандай да бір нақтылы х = х0 нүктесінде (2) қатарды зерттеу үшін, оның
дербес қосындысын құрамыз:

Содан кейін ат мен bm орнына олардың интегралдық өрнектерін (1) қоямыз
және тұрақты cos mx0, sin mx0 сандарын интеграл таңбасының астына аламыз:
Мына теңбе-теңдікті тексеру оңай:

Интеграл астындағы өрнекті түрлендіру үшін бұларды пайдаланып, ақырында
табатынымыз
(3)
Бұл интегралды Дирихле интегралы деп атайды.
Біз бұл жерде периоды , и айнымалысының функцияларымен айналыстық,
ал интегралдау аралығын жоғарыда айтылған ескерту бойынша, мысалы
аралығымен алмастыруға болады:

t = u — x0 деп ауыстырып, бұл интегралды

түрінде жазамыз.
Бұдан кейін интегралды екіге бөліп: және екінші интегралды да айнымалы
таңбасын өзгерту жолымен аралығына келтіріп, Фурье қатарының дербес
қосындысы үшін мынадай ақтық өрнекті табамыз:
(4)
Сонымен, біз ақырында параметр п енетін тап осы интегралдың сипатын
зерттейтін боламыз.
Біздің алдымызға қойылып отырған мәселенің ерекшелігі сол, бұл жағдайда
интеграл таңбасының астында шектік көшудің қолданылуы мүмкін емес.

§ 5. Функциялардың ортогональ жүйелері.

Анықтама. [a, b] аралығында анықталған және көбейтіндісінің интегралы
нөлге тең мен функциялары сол аралықта ортогональды деп
аталады:

[a, b] аралықта анықталған және онда үзіліссіз болатын не санаулы
нүктелерде үзілісті болатын функциялар жүйесін қарастырайық.
Егер берілген жүйенің функциялары қос-қостан ортогональ болса, яғни

(15)

онда жүйе функциялардың ортогоналъ жүйесі деп аталады. Мұнда біз әрқашан да

(16)
шарттары орындалғанда жүйе қалыпты деп аталады. Ал бұл шарттар
орындалмағанда, қажет деп тапсақ, системасына ауысуға болады, ал
бұның қалыпты екендігі белгілі.
Функциялардың ортогональды жүйенің маңызды мысалы жоғарыда
қарастырылған аралығындағы
1, cos x, sin x, cos 2x, sin 2x, ..., cos nx, sin nx,
... (17)
тригонометриялық жүйені келтіруге болады, мұның ортогональдылығы, синус
және косинус функцияларының 40 қасиеттерінен, яғни (6), (8), (9) және
(13) қатыстардан шығады.
Алайда ол (10) және (14) себепті қалыпты бола алмайды. Тригонометриялық
(17) функцияларды тиісті көбейткіштерге көбейтіп, қалыпты жүйені шығарып
алу оңай:

Айталық, [a,b] аралығында қандай да бір ортогональды системасы
берілген делік.
Енді [a, b] аралығында анықталған f(x) функциясын функциялары
бойынша қатарға мына түрде жіктейік:
(18)
Бұл жіктелудің коэффициенттерін анықтау үшін, жіктелудің өзін мүмкін дей
отырып, біз жоғарыда дербес жағдайда орындағанымыздай істейміз. Атап
айтқанда, жіктелудің екі жақ бөлігін де -ке көбейтіп, оны мүшелеп
интегралдаймыз:

Ортогональды болғандықтан [(15) және (16) қараңыз, оң жақ бөлікте тұрған
біреуінен өзге интегралдардың барлығы да нольдер болады да:

(7), (11), (12) формулалар осы формуланың дербес жағдайлары болмақ.
Коэффициенттері (19) формулалар бойынша құрылған (18) қатар берілген
функцияның жалпыланған Фурье қатары деп, ал коэффициенттердің өздері — оның
жүйесіне қатысты жалпыланған Фурье коэффициенттері деп аталады.
Жүйе қалыпты болған жағдайда (19) формулалардың түрі қарапайым; сонда

(19a).
Әрине, мұнда да жоғарыда айтылған ескертпелерді қайталауға болады.
Берілген f (x) функциясы үшін құрылған жалпыланған Фурье қатары онымен тек
формальды түрде ғана байланысты. Ал жалпы жағдайда f (x) функциясы мен оның
Фурье қатарының арасындағы байланыс былай белгіленеді:
~
(18a)
Бұл қатардың f(x) функциясына жинақтылығын, тригонометриялық қатар
жағдайындағыдай, әлі де зерттеу қажет.
Сонымен, біз қарастыратын синус және косинус функцияларынан құралған
тригонометриялық жүйедегі барлық функциялар өз-ара ортогональ болғандықтан,
бұл жүйе ортогональ жүйе болады.

§ 6. Фурье коэффициенттері туралы Риман теоремасы.

Берілген [a, b] аралығында үзіліссіз немесе санаулы нүктелерде үзілісті
болатын функцияны Фурье қатарына жіктегенде осы қатардың коэффициенттері
жайында қандай тұжырым айтуға болады? Осы сұраққа келесі теорема жауап
береді.
Теорема1. Егер g(t) функциясы қандай бір шектеулі [a, b] аралығында
үзіліссіз не үзінді-үзіліссіз болса, онда

және,

Теореманы дәлелдемес бұрын, теорема тұжырымындағы интеграл ішіндегі функция
көбейтінділері Фурье коэффициенттерін беретіндігін ескеру қажет.
Дәлелдеуі.
Біріншіден, g(t) функциясын үзіліссіз деп ұйғарып, бірінші тұжырымды
дәлелдейік.
Алдымен шектеулі аралығы қандай болса да, былай бағалауға болатынын
ескертеміз:
(5)

аралығын
(6)
нүктелермен п бөлікке бөлеміз және осыған сәйкестендіріп интегралды да
қосындыларға жіктейміз:

g(t) мәндерінің t-ші аралықтағы ең кішісін mt арқылы белгілеп, бұл өрнекті
былай түрлендіруге болады:

Егерде g(t) функциясының t-ші аралықтағы тербелісі болса, онда ол
шекаралықта болады; (5) теңсіздіктерді ескере отырып, енді алынған
интеграл үшін оңай баға шығарып алуға болады:

Кез келген санын алып, алдымен

болатындай етіп, (6) бөлуді таңдап аламыз, сонда

g функциясы үзіліссіз болуы себепті бұлай істеуге болады. Енді, mt сандары
сонымен бірге анықталатын себепті, былай алуымызға болады:

және осы р мәндері үшін табатынымыз

сөйтіп, біздің ұйғарымымыз дәлелденді.
Егер Фурье коэффициенттерін өрнектейтін (1) формулаларды еске
түсіретін болсақ, онда бұдан тікелей шығатын алғашқы салдар ретінде мынадай
ұйғарымды айтуға болады:
Салдар1. Үзінді-үзіліссіз функцияның Фурье коэффициенттері am ,bm ,
жағдайда нөлге ұмтылады.
Дәлелденген Риман теоремасынан тікелей шығатын келесі екінші
салдар локализация ұстамы делінетін ұғым.
Теорема. f(x) функциясына құрылатын Фурье қатарының қандай да х0
нүктесіндегі сипаты қарастырылатын нүктеге жақын жерде, яғни мейлінше
кішкене төңіректе, тек осы функцияның қабылдайтын мәндеріне байланысты
болады.
Дәлелдеуі.
Кез келген оң сан алып, (4)-дегі интегралды екіге бөлеміз:

Егер екінші интегралды мына түрде қайта жазсақ:

онда синус жанындағы көбейткіш

аралықта -нің үзінді-үзіліссіз функциясы болатыны айқын, өйткені
бөлшектің алымында тұрған -нің функциясы сондай және бөліміндегі бұл
аралықта нөлге айналмайтын өрнек үздіксіздігін сақтап қалады. Олай
болғанда лемма бойынша бұл интеграл жағдайда нөлге ұмтылады, сонымен
Фурье қатарының дербес қосындысы, sn(x0), үшін шектің бар болуы және бұл
шектің шамасы тек бір ғана интегралдың сипатына байланысты анықталады, яғни

Алайда бұл интегралға тек f(x) функциясының аргументтің -дан -ға
дейінгі аралықтағы өзгерісіне сай мәндері ғана енеді Осы қарапайым
түсініктер арқылы локализация принципі дәлелденеді.
Сонымен, егер, мысалы, кез келген кішкене х0 төңірегінде мәндері
бірдей болатын екі функция алсақ, онда олардың бұл төңіректен тыс аралықта
қаншалықты айырмашылығы болса да, бұл функцияларға сәйкес Фурье қатарлары
х0 нүктесінде бірдей сипатты болады: не екеуі де жинақталады және тек бір
ғана қосындыға жинақталады, не екеуі де жинақсыз болады.
Егер қарастырылып отырған функциялардың Фурье коэффициенттерінің
өздері, олардың барлық мәндеріне тәуелді бола тұра, тіпті әр түрлі болуы
мүмкін екенін еске алсақ, бұл қорытындыға таңданбасқа болмайды.
Бұл теорема әдетте Риман атымен бірге аталады, өйткені бұл 1853 жылы
дәлелденген оның жалпылау теоремасының салдары болып табылады. Алайда,
локализация принципі идеясы Остроградскийдің 1828 жылы жарық көрген
математикалық физика жөніндегі бір еңбегіне енгенін атап өткен жөн, сондай-
ақ, Лобачевскийдің 1834 жылы тригонометриялық қатарлар жөніндегі
зерттеулерінде байқалған-ды

§ 7. Периодты емес функцияларды Фурье қатарына жіктеу.

Жоғарыда бүкіл теорияны құрғанда, берілген функция -тің барлық
нақты мәндерінде анықталған деп және де периоды деп жорылған еді.
Алайда, көптеген қолданбалы математиканың және физиканың есептерін шығару
барысында қандай да бір аралықта, мысалы аралығында периодты
функциялармен қатар периодты емес, периодты дерлік функцияларды қолдануға
тура келеді.
Периодты емес функцияға жоғарыда баяндалған теорияны қолдана
алатын болу үшін, оның орнына көмекші функциясын енгіземіз, бұл
былайша анықталған: аралықта біз пен -ті теңбе-тең деп
аламыз:

(12)
бұдан кейін

деп аламыз, ал х-тің қалған нақты мәндерінде f*(x) функциясын периодтылық
заңы бойынша қарастырамыз.
Осылайша құрылған периодты f*(x) функциясына дәлелденген жіктеу
теоремасын енді қолдануға болады. Алайда, егер — мен -дің тек
аралығында жатқан х0 нүктесін алатын болсақ, онда (12) бойынша біз берілген
f(x) функциясына келер едік. Нақ сол себептен жіктеу коэффициенттерін де,
f*(x) функциясына ауыспай-ақ, (1) формулалар бойынша есептеп шығаруға
болады.
Қысқаша айтқанда, жоғарыда дәлелденгендердің барлығы да, көмекші f*(x)
функциясының қатысынсыз, берілген f(x) функциясына тікелей ауысады.
Алайда аралықтың ұштарындағы х= ± нүктелерге ерекше назар аудару
қажет. f*(x) функциясына жоғарыдағы теореманы қолданғанда, айталық, х=
± нүктесінде -дің сол жағында көмекші f*(x) функциясының
берілген f(x) функциясының сәйкес мәндерімен дәл келетін мәндерін, ал
-дің оң жағындa f*(x) функциясының енді -дің оң жағында f(x)
мәндерімен дәл келетін мәндерін қарастырар едік. Сондықтан үшін S0
мәні ретінде

деп алуға тиісті боламыз.
Сонымен, егер берілген f(x) функциясы, х= ± болғанда тіпті үздіксіз
болып, бірақ периоды болмаса, болады, онда үзінді-
дифференциалдану үшін қойылатын шарттарды ескергенде — Фурье қатарының
қосындысы мына сан

болады да бұл -ден де және -ден де өзгеше. Мұндай функция үшін
тек ашық аралығына ғана жіктелу мүмкін болады.
Ескерту. Егер тригонометриялық (2) қатар аралықта f(x)
функциясына жинақты болса, онда, оның мүшелерінің периоды болатын
себепті, ол барлық жерде жинақты болады және оның S(x) қосындысы да -
тің периодты функциясы болып, периоды болады.
Бірақ бұл қосынды көрсетілген аралықтың сыртында f(x) функциясымен дәл
келмейді f(x) функциясы бүкіл нақты осьте берілген жағдайда. Ақтығында,
аралықтың орнына ұзындығы болатын кез келген аралықты
алуға болатынын ескертеміз.

§ 8. Кез келген аралықта берілген ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.