Функциялардың жалпыланған Фабер-Шаудер жүйесі бойынша қатарларға жіктеулерінің қасиеттері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 37 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ... 3

1 Жалпыланған Хаар және жалпыланған Фабер-Шаудер жүйелері ... ... ... 10
1.1 Хаар жүйесі
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ...10
1.2 Жалпыланған Хаар
жүйелері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .1
3
1.3 Фабер-Шаудер
жүйесі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... .15
1.4 Жалпыланған Фабер-Шаудер
жүйелері ... ... ... ... ... ... ... ... ... ... ... ... ...24

2 Функциялардың жалпыланған Фабер-Шаудер жүйесі бойынша қатарларға
жіктеулерінің қасиеттері
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..29
2.1 Жалпыланған Фабер-Шаудер функциялар жүйесінің базистік
қасиеті ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ... .29
2.2 Функциялардың жалпыланған Фабер-Шаудер жүйесі бойынша қатарларға
жіктеулерінің қасиеттері ... ... ...
... ... ... ... ... ... ... ... ... ... . ... ... ... ... 32
2.3 Жалпыланған Фабер-Шаудер жүйесі бойынша қатарлар үшін жалғыздық
жиыны ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ..37
2.4 Жалпыланған Фабер-Шаудер жүйесі бойынша кемтікті қатарлар ... ..40

3 Фабер-Шаудер жүйесінің квазигриди
базистілігі ... ... ... ... ... ... ... ... ... ... ..43

Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... 47

Пайдаланылған әдебиеттер
тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
..48

Кіріспе

Тақырыптың өзектілігі. Техниканың, физиканың әр түрлі салаларында
кездесетін ақпараттарды, сигналдарды т.с. өңдеп зерттеу үшін гармониялық
талдау әдістері кеңінен қолданылады. Гармониялық талдау күрделі
байланыстарды жақсы зерттелген ыңғайлы функциялар жүйесі бойынша жіктеуге
негізделеді. Аталған жүйелер қатарында Фабер-Шаудер жүйесі үлкен орын
алады. Зерттеу жалпыланған Фабер-Шаудер жүйесіне жіктеу қасиеттеріне
арналған.
Диссертациялық жұмыстың мақсаты. Фабер-Шаудер жүйесін құрайтын Ф{pn}
функциясының жаңа Ф класс жүйесінде функцияларды қатарларға жіктеулердің
қасиеттерін қарастырып, дәлелдеу.
Диссертациялық жұмыстың міндеттері:
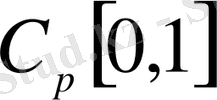функционалдық кеңістікте жалпыланған Фабер-Шаудер жүйесі бойынша
ең жақсы жуықтамдардың үзіліссіздік модулі арқылы бағалауын алу.
Жалпыланған Фабер-Шаудер жүйесі бойынша құрылған қатардың мүшелеп
дифференциалдану шартын келтіру.
Зерттеу пәні. Функциялардың жалпыланған Фабер-Шаудер жүйесі бойынша
қатарларға жіктеулерінің кейбір қасиеттері.
Зерттеу нысаны. Берілген жұмыста зерттеу объектісі ретінде жалпыланған
Хаар мен жалпыланған Фабер-Шаудер жүйелері алынды.
Зерттеу жұмысының практикалық маңыздылығы. Жұмыстың теориялық сипаты
және практикалық маңызы бар. кәзіргі замандағы көптеген техникалық,
физикалық әр түрлі үрдістерді математикалық модельдеуде кездесетін
ақпараттарды, сигналдарды т.с. өңдеп зерттеу үшін гармониялық талдау
әдістері кеңінен қолданылады. Гармониялық талдау күрделі байланыстарды
жақсы зерттелген ыңғайлы функциялар жүйесі бойынша жіктеуге негізделеді.
Диссертациялық жұмыстың барлық қорытындылары дәлелденген, теоремалар және
леммалар түрінде тұжырымдалған.
Зерттеудің ғылыми жаңалығы. Диссертациялық жұмыста келесі түрдегі
жаңалық нәтижелері алынды:
Функциялардың жалпыланған Фабер-Шаудер жүйесі бойынша қатарларға
жіктеулерінің кейбір қасиеттері, 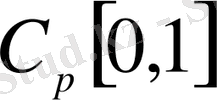функционалдық кеңістікте жалпыланған
Фабер-Шаудер жүйесі бойынша ең жақсы жуықтамдардың үзіліссіздік модулі
арқылы бағалауы алынған, жалпыланған Фабер-Шаудер жүйесі бойынша құрылған
қатардың мүшелеп дифференциалдану шарты келтірілген.
Зерттеуді сынақтан өткізу. Негізгі нәтижелер келесі конференцияларда
мақалалар мен тезистер түрінде жарияланды:
Халықаралық ғылыми-практикалық конференция Шоқан тағылымы-13
(Көкшетау, 2008);
Международная научно-практическая конференция, Наука и ее роль в
современном мире, (Караганда 2009);
Международная научная конференция студентов, магистрантов и молодых
ученых, Ломоносов-2008, тезисы докладов, (Астана 2008);
Халықаралық ғылыми-практикалық конференция Шоқан тағылымы-14
(Көкшетау, 2009);
Математика және ОӘ кафедрасының семинарларында баяндама жасалып,
талқыланды.
Зерттеу әдістері: Функционалдық кеңістіктер қасиеттерін қолданып,
гармониялық талдау әдістемелері негізінде зерттеулер жүргізілген.
Қорғауға ұсынылатын қағидалар:
Диссертациялық жұмыс функциялардың жалпыланған Фабер-Шаудер жүйесі
бойынша қатарларға жіктеулерінің қасиеттерін зерттеуге арналған. Онда
функциялардың кейбір класстары: Хаар жүйесі мен жалпыланған Хаар жүйелері,
Фабер-Шаудер жүйесі мен Жалпыланған Фабер-Шаудер жүйелері, жалпыланған
Фабер-Шаудер функциялар жүйесінің базистік қасиеті, функциялардың
жалпыланған Фабер-Шаудер жүйесі бойынша қатарларға жіктеулерінің
қасиеттері, қатарлар үшін жалғыздық жиыны, кемтікті қатарлар және Фабер-
Шаудер жүйесінің квазигриди базистілігі қарастырылады.
1909 жылы Хаар құрған классикалық Хаар жүйесі ортогональ қатарлар
теориясы мен оның есептеу техникаларында қолданылуында, ықтималдықтар
теориясы мен басқаларда маңызды рөл атқарады. Уолш жүйесі мен
тригонометриялық жүйелерден айырмашылығы Хаар жүйесі бойынша үзіліссіз
функциялар Фурье-Хаар қатары [0,1] кесіндісінде бірқалыпты жинақталады және
Хаар жүйесі бойынша қосындылы функциялар Фурье-Хаар қатары [0,1]
кесіндісінің барлық жерінде 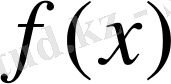-ке жинақталады.
Фурье-Хаар қатарларының көптеген қасиеттері Г.Алексеич, С.Качмаж,
Г.Штейнгауз, Б.С.Кашин, А.А.Саакян монографияларында және Б.И.Голубов шолу
мақаласында [17] зерттелген. Фурье-Хаар қатарларының қасиеттерін зерттеуге
И.Шаудер, П.Л.Ульянов, И.Марцинкевич, Б.И.Голубов, В.А.Скворцов,
С.В.Бочкарев және тағы басқа авторлар жұмыстары арналған.
1958 жылы Н.Я. Виленкин [11] алғаш рет құрамында Хаар жүйесі бар
ортогональ жүйелер кластарын қарастырды. 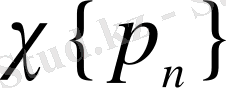жүйесі , 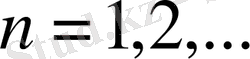бүтін
тізбегімен анықталды. және 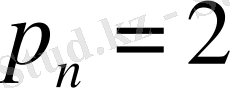, 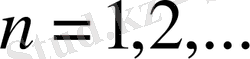болғанда Хаар жүйесімен сәйкес
келеді. Осы класс жүйелерін жалпыланған Хаар жүйесі деп, ал 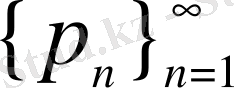тізбегін
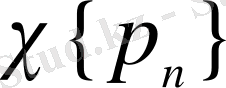жүйесін жасаушы деп атайды. 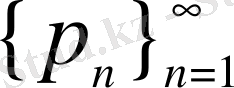жасаушы тізбегінің шенелген болған
жағдайда 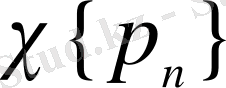Хаар жүйесінен белгілі көптеген нәтижелер жалпыланған Хаар
жүйелеріне де сақталады. 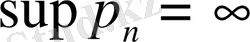болған жағдайда басқа нәтижелер де орын алуы
мүмкін.
Жалпыланған Хаар бойынша Фурье қатарларының әр түрлі қасиеттерін
Б.И.Голубов пен А.И. Рубенштейн [19], ( 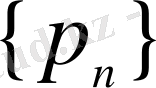жасаушы тізбегінің шенелген
болу шарты орындалғанда, яғни , 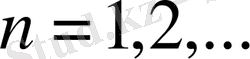), Б.И.Голубов [16] (кез келген
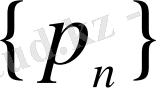жасаушы тізбектермен), Е.А. Власова [12], Е.С. Смаилов пен
С.Тазабеков [29-31], Н.А. Бокаев [9], Г.А.Акишев [1,2] және басқалар
зерттеген.
1910 жылы Г.Фабер ([43]), 1927 жылы Д.Шаудермен ([48]) қайта ашылған
қазіргі әдебиеттерде Фабер-Шаудер жүйесі атауына ие функция жүйесін
кұрды. ([23] қараңыз). Үзіліссіз, құрама-сызықтық функциялардан құрылған
бұл жүйе [0,1] кесіндісінде үзіліссіз функциялар кеңістігінде қарапайым
базистің бірі болып табылады. Кейіннен осы жүйе бойынша функцияларды
қатарларға жіктеулерінің әр түрлі қасиеттерін бірқатар авторлар
П.Л.Ульянов, В.А.Матвеев, С.В.Бочкарев, Т.Н.Сабурова, А.П.Горячев және
З.Чисельский зерттеген.
Соңғы онжылдықта 1998-2007 жылдары Т.У.Аубакиров пен Н.А. Бокаев
жалпыланған Фабер-Шаудер жүйесін енгізіп, функциялардың жалпыланған Фабер-
Шаудер жүйесі бойынша қатарларға жіктеулерінің қасиеттерін зерттеген [6],
[7].
Осы жұмыстың нәтижелерін баяндаудан бұрын жалпыланған Хаар және Фабер-
Шаудер жүйелерінің қысқаша анықтамасын және олардың арасындағы байланысты
қарастыра кетейік. (толық мағлұмат бірінші бөлімде келтірілген).
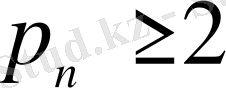
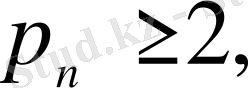
Әрбір жүйе p0=1, а 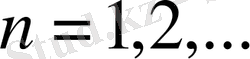болатын {pn} натурал сандар тізбегімен
анықталады.
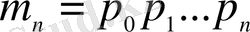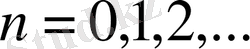, деп алсақ, онда әрбір 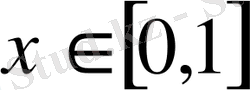\Q нүкте үшін
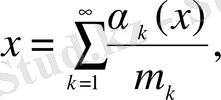
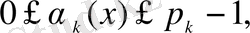
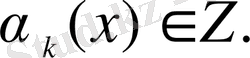(0.1)
жалғыз жіктеу бар болады, мұндағы , , .
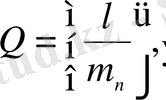
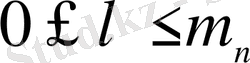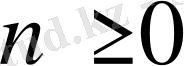Әрбір бүтін 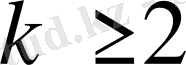саны
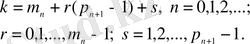(0.2)
жалғыз түрде беріледі.
[0,1] кесіндісінд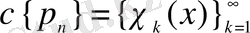е және 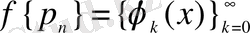функциялар жүйесін келесі түрде
анықтайық ([19] және [7] қараңыз).

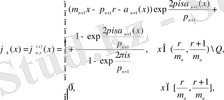
мұндағы 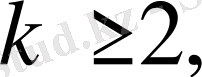n,r,s (0.2) теңдіктен.
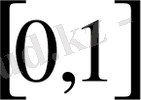\Q жиыны 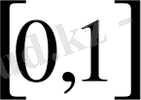кесіндісінде тығыз орналасқанын қолдана отырып,
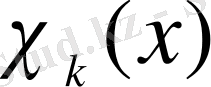функциясын 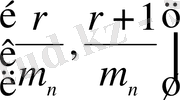оң жақ жартылай интервалында үзіліссіздік бойынша
жалғастырайық, ал x=1 нүктесінде 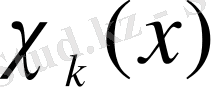функциясын кесінді ішінде оның
шектік мәніне тең деп аламыз.
Ескерту. 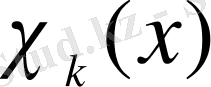функциясының үзіліс нүктесінде оң және сол жақ
шектерінің жартылай қосындысына тең болатын 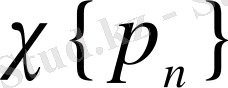жүйесіне келтірілген
анықтама көпшілік мақұлдаған анықтамадан ерекшелінеді (мысалы, [19]
қараңыз).
[0,1] кесіндісінде 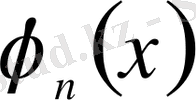функциясын үзіліссіздік бойынша жалғастырамыз.
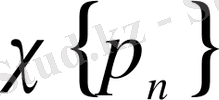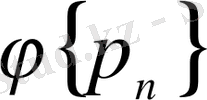Сол себептен, және жүйелері толығымен анықталды және
n=1,2,... жағдайда сәйкесінше Хаар (алдыңғы ескертуді ескерген жағдайда) және
Фабер-Шаудер классикалық жүйелерімен сәйкес келеді. Анықтамалардан тікелей
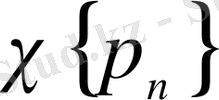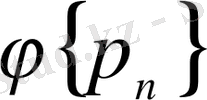және жүйелері арасында байланыс шығады:
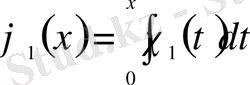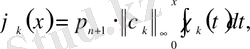
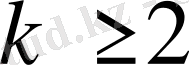, (0.3)
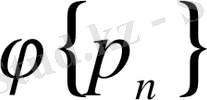жүйесі бойынша
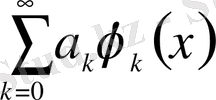(0.4)

қатарын қарастырайық. Егер (0.4) қатар f(x) ақырлы функциясына барлық
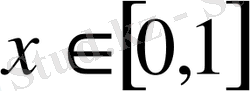нүктесінде жинақталса, онда 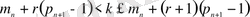болғанда ,
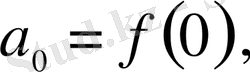
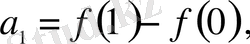
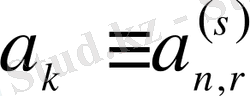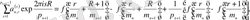(0.5)
.
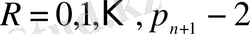теңдеулер жүйесінен табылады.
Өз кезегінде
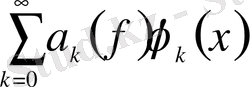, (0.6)
қатары, мұндағы 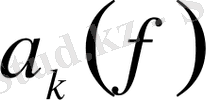(0.5) формуласы бойынша есептеледі, әрбір
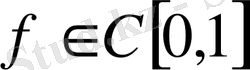функциясы үшін f(x) –ке [0,1] аралығында бірқалыпты жинақталады. ([7]
қараңыз). (0,6) қатардың 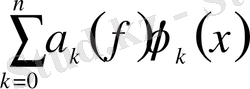дербес қосындысын 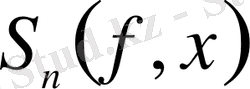деп белгілейміз.
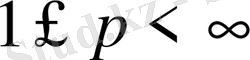және f(x) функция [0,1] аралығында анықталған, ал 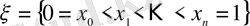- [0,1]
кесіндісін бөліктеуі болсын. Анықтама бойынша ([32] қараңыз):
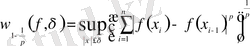, (0,7)
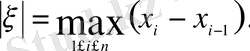
мұндағы 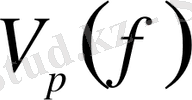арқылы 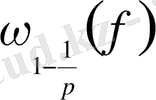-ді белгілейік.
Айталық, егер 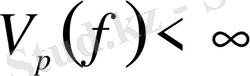болса f функция 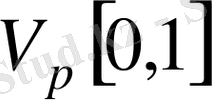, 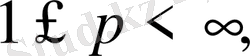кеңістігінде жатады және
егер 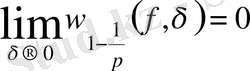болса, онда 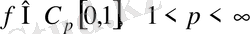болады. Нормасы

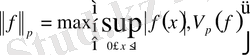
болатын 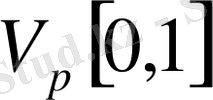және 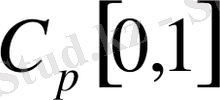кеңістіктері банах кеңістіктері болады.
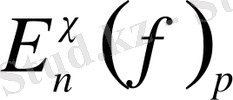және арқылы сәйкесінш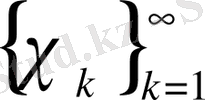е және 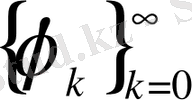жүйелері бойынша
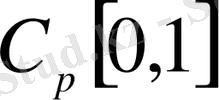метрикасындағы n-ші реттен үлкен емес көпмүшелері бар 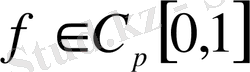функциясының ең
жақсы жуықтамдарын белгілейміз. 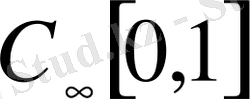кеңістігі 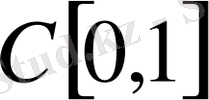үзіліссіз функциялар
кеңістігімен тепе-тең. 1 p болғанда 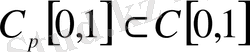енгізу орындалады.
функциясының үзіліссіздік модулі
.
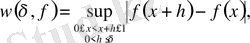
теңдігімен анықталады.
Бірінші бөлімде Хаар жүйесі мен жалпыланған Хаар жүйелері және Фабер-
Шаудер жүйесі мен жалпыланған Фабер-Шаудер жүйелерінің анықтамалары
келтіріледі.
Енді екінші бөлімнің нәтижелеріне тоқтала кетейік.
Осы бөлімде функциялардың жалпыланған Фабер-Шаудер жүйесі бойынша
қатарларға жіктелулерінің қасиеттері қарастырылады.
2.1 параграфта жалпыланған Фабер-Шаудер функциялар жүйесінің базистік
қасиеті қарастырылады. Келесі теорема дәлелденеді
Теорема 2.1 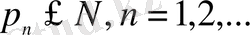болатын 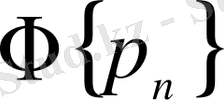жүйесі кеңістігінде базис болып
табылады. Сонымен қатар, егер де 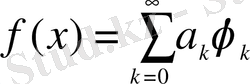, болса, онда келесі бағалар
орындалады.

.
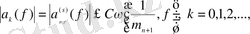
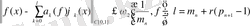2.2 параграфта функциялардың жалпыланған Фабер-Шаудер жүйесі бойынша
қатарларға жіктелулерінің қасиеттері туралы айтылады.
Мүшелеп дифференциалданған қатардың жинақтылығы
Теорема 2.3 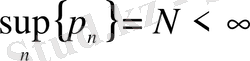болсын және

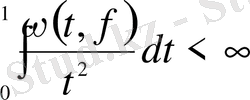
шарт орындалсын. Онда мүшелеп дифференциалданған (0,6) қатар [0,1]
кесіндісінің барлығында 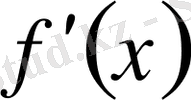-ке жинақталады.
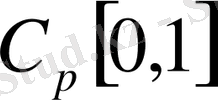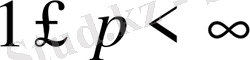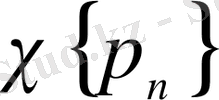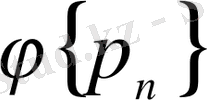, кеңістігінің функцияларын және жүйелері
бойынша құралған көпмүшелермен жуықтау
Теорема 2.4 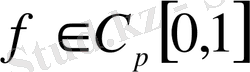және 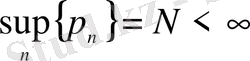болсын. Онда келесі теңсіздіктер
орындалады:

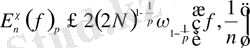
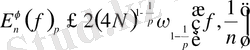
Мұндағы 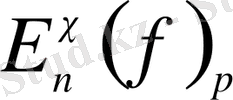және арқылы сәйкесінш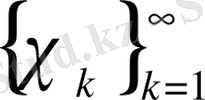е және 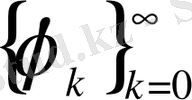жүйелері
бойынша 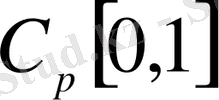метрикасындағы n-ші реттен үлкен емес көпмүшеліктері бар
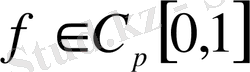функциясының ең жақсы жуықтамдарын белгілейміз.
2.3 параграфта жалпыланған Фабер-Шаудер жүйесі бойынша қатарлар үшін
жалғыздық жиыны қарастырылады.
Анықтама 2.2 Егер (3) қатарының 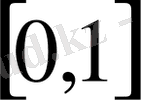\Е –де нөлге жинақтылығынан ,
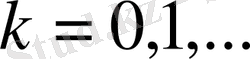болса, онда 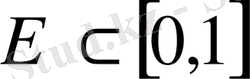жиыны U жиыны немесе

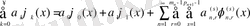
қатары үшін жалғыздық жиыны деп аталады
Теорема 2.5. Е жиыны Ф{pn} қатарлар үшін жалғыздық жиыны болуы үшін
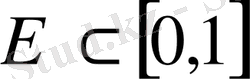\Q болуы қажетті және жеткілікті.
Теорема 2.6 Егер Ф{pn} жүйесі бойынша қатарлар
, ,
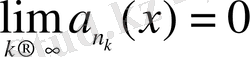шартын қанағаттандырса, мұндағы 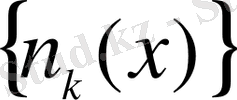– тұғырлары х қамтитын барлық
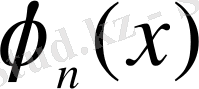функцияларының өспелі тізбек нөмерлері, онда 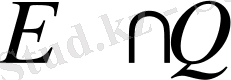болатын 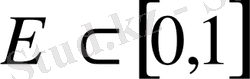жиыны
осындай қатарлар үшін жалғыздық жиыны болады.
Теорема 2.7 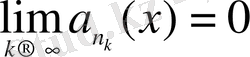, шарт орындалатын Ф{pn} жүйесі бойынша қатарлар
үшін саналымды жиын жалғыздық жиын болады.
2.4 параграфта жалпыланған Фабер-Шаудер жүйесі бойынша кемтікті
қатарлар туралы айтылады.
А.А. Саакян C[0,1] кеңістігінен алынған әрбір f(x) функция үшін λ(х)
айнымалыны ауыстыруды f(λ(х)) функциясының Фабер-Шаудер бойынша кемтіктік
қатар болатындай таңдап алуға болатынын көрсетті [27] (сонымен қатар [23]
қараңыз). Баяндамада 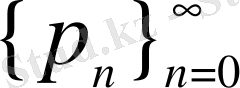шенелген натурал сандар тізбегінен құрылған
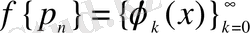функциялар жүйесінде де осындай қасиеттер орындалатыны көрсетілген.
Теорема 2.8 f(x)C[0,1], f(0)=f(1)=0 және 1n0n1... – натурал
сандар тізбегі болсын. Онда 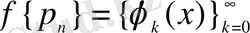функциялар жүйесі бойынша F(x)=f(λ(х))
суперпозициясын жіктеу 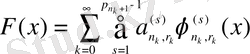болатындай rk, 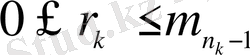, k=0,1,...нақты сандар
және [0,1] кесіндісінді үзіліссіз 0xy1 болғанда 0=λ(0)λ(x)λ(y)λ(1)=1
шарты орындалатын λ(x) функциясы бар болады.
Үшінші бөлімде Гриди алгоритмін енгізіп, Фабер-Шаудер жүйесінің
квазигриди базистілігі қарастырылады.
Банах кеңістіктері үшін Гриди алгоритмдерін нормаланған базиске қатысты
Конягин, Темляков [45], ДеВор [41], Войтащик [49], Григорян [21,42] және
басқалар зерттеген ([15,40] қараңыз).
Қорытындыда ғылыми болжамды дәлелдейтін зерттеудің нәтижелері
мазмұндалады.
Жұмыс тақырыбы бойынша басылымдар:
Аубакиров Т.У., Рахимжанова Ф.К. Приближение функций ограниченной
вариации полиномами по обобщенной системе Фабера-Шаудера. Шоқан тағылымы-
13 Т.6, Көкшетау, 2008, 156-158 бет;
Аубакиров Т.У., Рахимжанова Ф.К. О рядах по обобщенной системе Фабера-
Шаудера.Материалы межд.научо-практической конференции, т.4, Караганда
2009, 279-282бет;
Рахимжанова Ф.К., Аубакиров Т.У. О лакунарных рядах по обобщенной
системе Фабера ШаудераЛомоносов-2008, тезисы докладов, І часть, Астана,
44-45бет;
Аубакиров Т.У., Рахимжанова Ф.К. Разложения функций в ряд по обобщенной
системе Фабера-Шаудера. Шоқан тағылымы-14 Т.9, Көкшетау, 2009, 178-181
бет.
Диссертация құрылымы және көлемі. Диссертация кіріспеден, 3 бөлімнен,
қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады. Теоремалар мен
формуларды нөмірлеу екіорынды саннан тұрады, бірінші сан- бөлім нөмірі,
екіншісі - теорема мен формулалардың бөлім ішіндегі өз нөмері.

1. Фабер-Шаудер жүйесі мен жалпыланған Фабер-Шаудер жүйелері және Хаар
жүйесі мен жалпыланған Хаар жүйелері

1. Хаар жүйесі

Хаар жүйесін анықтаудан бұрын кейін барлық жерде қолданылатын
стандартты екілік интервалдарды белгілеу енгізейік. Екілік интервал деп
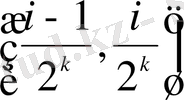, мұндағы 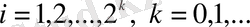түріндегі интервалдарды айтады.
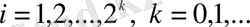, үшін

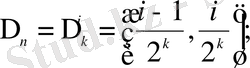
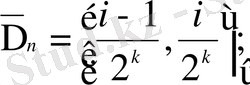
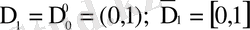(1.1)
Егер 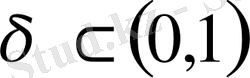- қандай болса да интервал, онда және арқылы
сәйкесінше 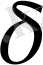интервалының оң және сол жақ жартылары белгіленеді (орташа
нүктені қоспағанда). Дербес жағдайда, (),
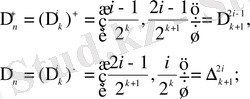(1.2)
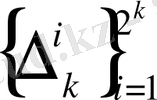интервалдарын біз k-ші бума интервалдары деп атайтын боламыз,
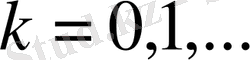. Екілік интервалдардың қарапайым қасиеттерін белгілейік:
1) 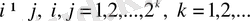болғанда 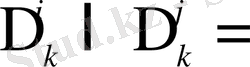Ø
2) Егер 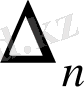мен 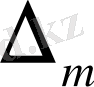- екілік интервалдар және 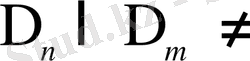Ø болса, онда 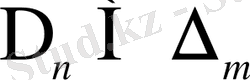не
, не 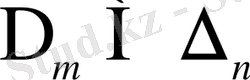болады.
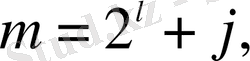
1) қасиет айқын, 2) қасиет , 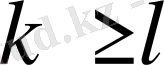болғанда
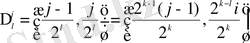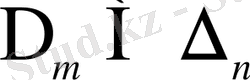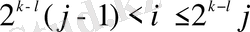теңдігіне қарағанда не (егер ), не 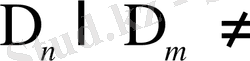Ø (егер 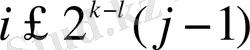, не
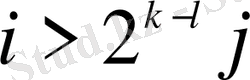) шығады.
Анықтама 1.1 Хаар жүйесі - 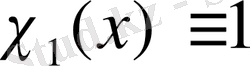болатын 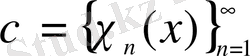, 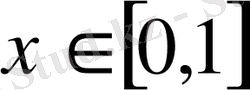функциялар
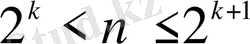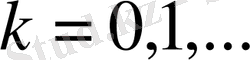
жүйесі, ал , 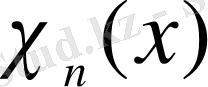функциясы былай анықталады:
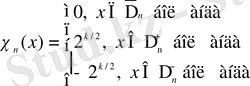(1.3)
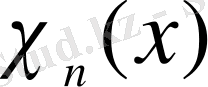мәні үзіліс нүктесінде және [0,1] кесіндісінің ұштарында
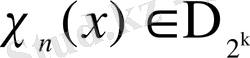болатындай таңдап алынады, яғни келесі теңдіктер орындалатындай:
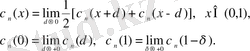(1.4)
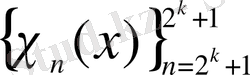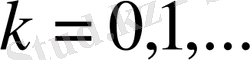, функциялар тобын к-ші бума деп атаймыз. Жиі Хаар жүйесінің
нөмерлерінің орнына берілген функция қандай бумаға жататынын көрсететін
нөмерлеуді қолданған ыңғайлы, дәлірек айтқанда, , ,
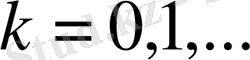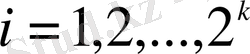болғанда
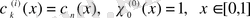(1.5)
Сонда, Хаар жүйесі 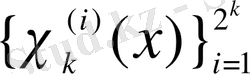, , 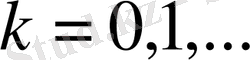және функциясының бумаларының
бірігуінен тұратыны түсінікті.
Екілік интегралдардың 1) және 2) қасиеттерінен тікелей Хаар жүйесі –
ортонормаланған жүйе екені шығады. Оның толықтығын дәлелдеу үшін
келесілерін белгілейік:
Тұжырым 1.1 , , 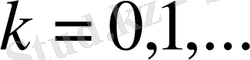үшін функцияларының қабықшасы -
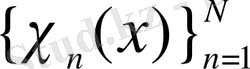
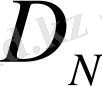мен сәйкес келеді, яғни , , 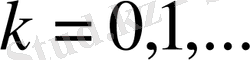болғанда:
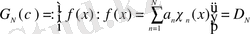(1.6)
Шынында да, Хаар функциялары сызықтық тәуелсіз (өйткені Хаар жүйесі –
ортонормаланған жүйе), сондықтан (1.6) теңдік және 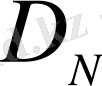- N -
өлшемді сызықтық кеңістіктер фактісінен шығады, сонымен бірге
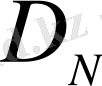((1.4) қараңыз).
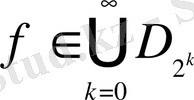функциялар жиыны 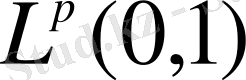, 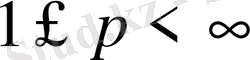кеңістіктерінде барлық жерде тығыз,
тұжырым 1-ден 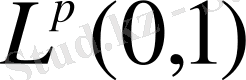, 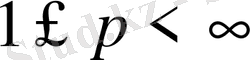кеңістіктерінде Хаар жүйесінің толықтығы шығады.
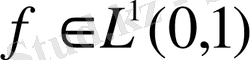функциясының Фурье-Хаар қатарының 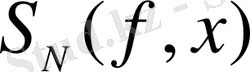дербес қосындылары үшін:

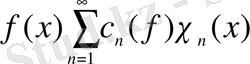
өрнегін табамыз, мұндағы 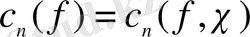- 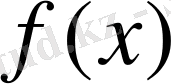функциясының Фурье-Хаар
коэффициенттері, сонымен бірге Хаар функциясының анықтамасы бойынша
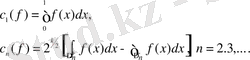(1.7)
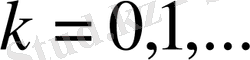, , болғанда
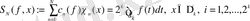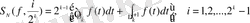; (1.8)
, (1.8)
, .
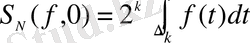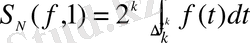болатынын дәлелдейік.
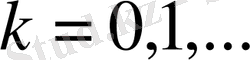үшін
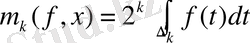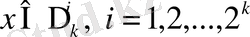, (1.9)
деп алып, 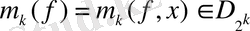функциясын анықтайық ( 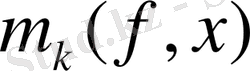функциясының мәндері үшін
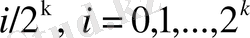нүктелерінде (1.9) теңдігімен және 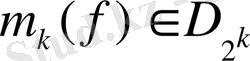шартымен бірмәнді анықталатыны
айқын).
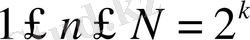болатын 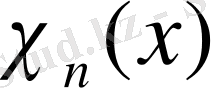функциялары және 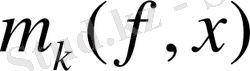функциясы 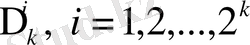барлық
интервалда тұрақты болатынын ескерсек, 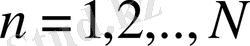болғанда

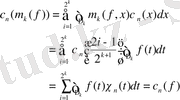
аламыз.
Осыдан
, .
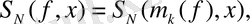
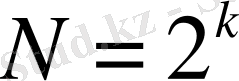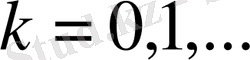Бірақ 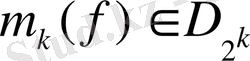және (6)-ға сәйкес, , сондықтан
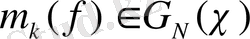
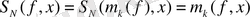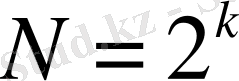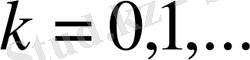, , . (1.10)
Осыдан (1.8) және (1.8) теңдіктер шығады.
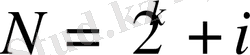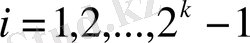
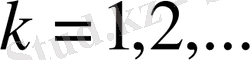, түрдегі N нөмерлі 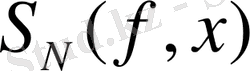дербес қосындылары үшін, екілік
интервалдардың 1) қасиетін ескеріп, келесі өрнекті аламыз:
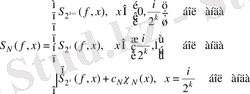(1.11)
Соңында 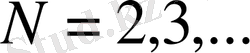болғанда (1.11) және (1.8) өрнектерінен:
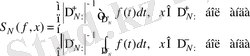(1.11)
теңдігі шығады.

2. Жалпыланған Хаар жүйелері

1909 жылы 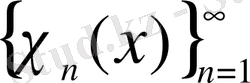функциясының ортогональ жүйесін Хаар енгізді [39], ол
келесі түрде анықталады:
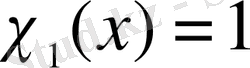, деп аламыз. әрбір 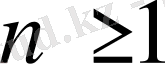санын , , 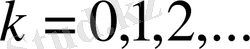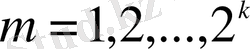түрде
ұсынып,

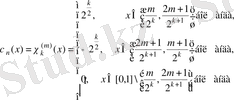
аламыз.
Үзіліс нүктелерінде Хаар функциялары оң жақты және сол жақты шектерінің
жартылай қосындысына тең болады, яғни

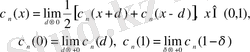
Хаар жүйесі ортогональ қатарлар теориясында маңызды рөл атқарады.
Хаар үзіліссіз функциялар Фурье-Хаар қатары [0,1] кесіндісінде
бірқалыпты жинақталатынын [39], 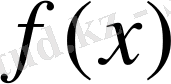қосындылы функциялар Фурье-Хаар
қатары [0,1] кесіндісінің барлық жерінде 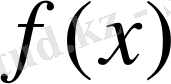-ке жинақталады.
Тригонометриялық жүйе осындай қасиеттерге ие емес екендігі белгілі [8].
Фурье-Хаар қатарларының көптеген қасиеттері [3], [18], [22], [23]
монографияларында және Б.И.Голубов шолу мақаласында [17] зерттелген. Фурье-
Хаар қатарларының қасиеттерін зерттеуге И.Шаудер, П.Л.Ульянов,
И.Марцинкевич, Б.И.Голубов, В.А.Скворцов, С.В.Бочкарев және тағы басқа
авторлар жұмыстары арналған.
1958 жылы Н.Я. Виленкин [11] алғаш рет құрамында Хаар жүйесі бар
ортогональ жүйелер кластарын қарастырды. Жалпыланған Хаар жүйелері
анықтамаларын келтірейік ([22] қараңыз).
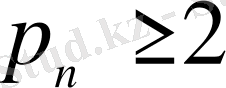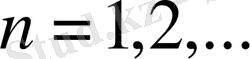, болатын кез келген 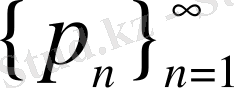бүтін сандар тізбегі берілген.
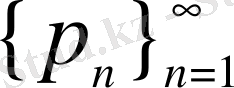тізбегінің көмегімен келесі түрде бүтін сандар тізбегін анықтайық
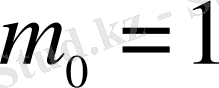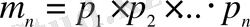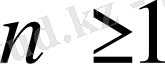; , (1.12)
[0,1] кесіндісінде 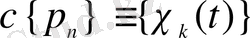жалпыланған Хаар жүйесін анықтайық. [0,1]
кесіндісінде 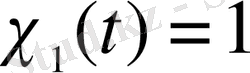деп аламыз. Әрбір 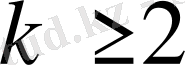бүтін саны
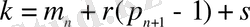(1.13)
; ;
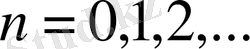түрде жалғыз беріледі.
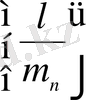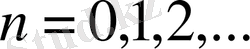- , , түрдегі нүктелер жиыны болсын, яғни
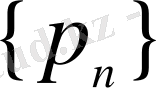рационал нүктелер. Сонда 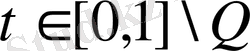әрбір санының
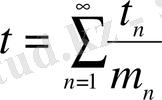, мұндағы 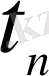-бүтін,
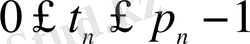(1.14)
түрде жалғыз жіктеуі болады.
(1.14) теңдікте берілген және (1.13) теңдікте берілге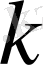н үшін

Әрі қарай жиыны [0,1] кесіндісінде барлық жерде тығыз болатынын
пайдаланып, 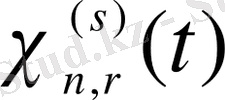функциясын үзіліссіздік бойынша 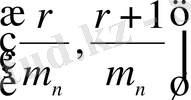интервалында
жалғастырамыз. Осыдан кейін үзіліс нүктелерінде 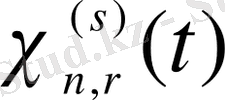функциясын оның оң
жақты және сол жақты шектік мәндерінің жартылай қосындысына тең деп, ал
[0,1] кесіндінің ұштарында – кесіндінің ішінен шектік мәндерге тең деп
аламыз.
Сол себептен, 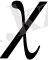класының 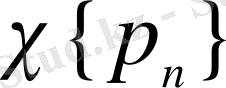жүйесі анықталд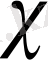ы. класы
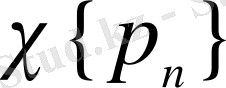барлық жүйелерінің жиынтығы. 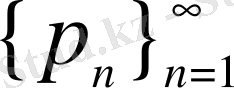тізбегін 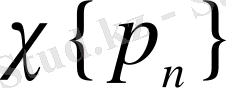жүйесін жасаушы деп, ал
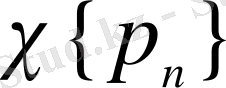жүйесін жалпыланған Хаар жүйесі деп атаймыз.
Егер барлық , (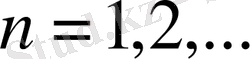) болса, онда 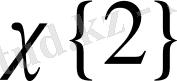жүйесі Хаар жүйесімен
сәйкес келеді ([35]).
Н.Я. Виленкин ([11], 476 бет) 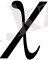класының 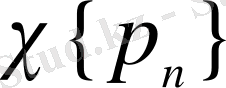жүйесі толық және
ортонормаланған болатынын көрсетті.
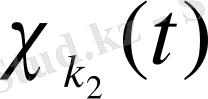функциясы 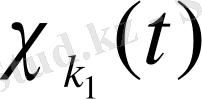функциясынан кейін шығады деп есептейміз, мұндағы
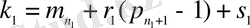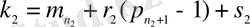, , келесі жағдайларда: 1) 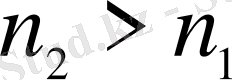не 2) , , 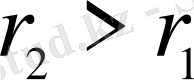не 3)
, , ал .
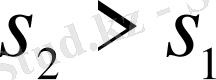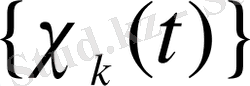жүйесінің анықтамасынан
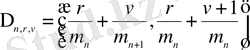, интервалдарында 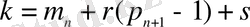, , 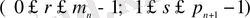болғанда 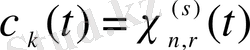функциясы ,
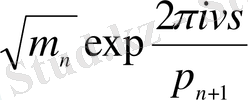-ге тең мән қабылдайтыны шығады, яғни 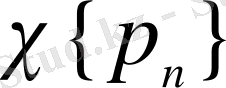функциялар жүйесі комплекс
мәнді сатылы функциялар болып табылады.
Жалпыланған Хаар жүйелері бойынша Фурье қатарларының әр түрлі
қасиеттерін Б.И.Голубов пен А.И. Рубенштейн [19], ( 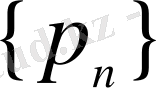жасаушы тізбегінің
шенелген болу шарты орындалғанда, яғни , 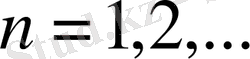), Б.И.Голубов [17] (кез
келген 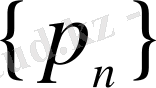жасаушы тізбектермен), Е.А. Власова [16], Е.С. Смаилов пен
С.Тазабеков [29-31], Н.А. Бокаев [9], Г.А.Акишев [1,2] және басқалар
зерттеген.

3. Фабер-Шаудер жүйесі

Анықтама 1.2 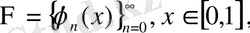функциялар жүйесі Фабер-Шаудер жүйесі деп аталады.
Ондағы
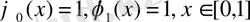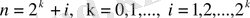және болғанда
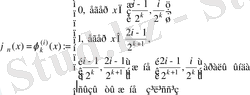(1.15)
Фабер-Шаудер жүйесін Хаар функциясын интегралдау арқылы да анықтауға
болады. Нақтырақ айтқанда
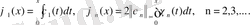(1.16)
теңдіктер орындалады.
Қатарды Фабер-Шаудер жүйесі бойынша қарастырайық:
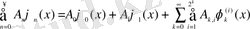(1.17)
және ол [0,1] кесіндісінің әрбір нүктесінде 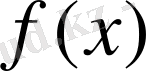шектік функциясына
жинақталады деп алайық. Онда 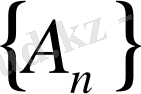коэффициенттері бір мәнді
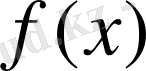функциясымен анықталатынын дәлелдейік, атап айтқанда егер
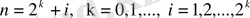болғанда
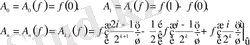(1.18)
болады.

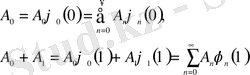
теңдіктерін пайдалана отырып ((1.15) қараңыз), біз 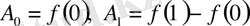екенін табамыз.
Егер де 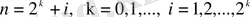болса, онда (1.15) сәйкес
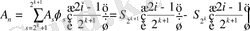(1.19)
мұндағы 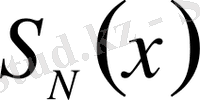- (1.17) қатардың дербес қосындысы:

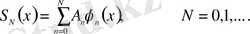
Егер 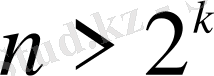болғанда (1.15)-ші жүйеден 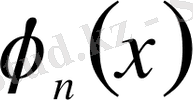функциялары
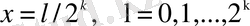нүктелерінде нөлге тең болатынын көреміз. Сондықтан 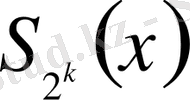, 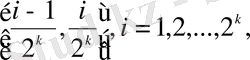әрбір
кесіндісінде сызықты болатынын ескерсек, онда (1.19) қатынастан

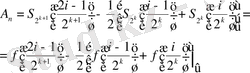
шығады.
Дәлелденген (1.18) формуласынан, дербес жағдайда 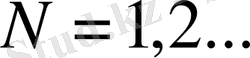болғанда [0,1]
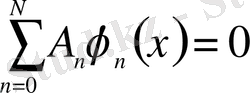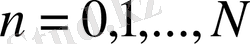аралығының барлық жерінде , , мұндағы болғанда ғана
орындалады, яғни 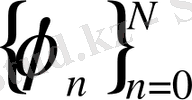функциялары сызықтық тәуелсіз. 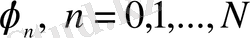функция
анықтамасынан ((1.15) қараңыз) және оның сызықтық тәуелсіздігінен келесі
тұжырым шығады:
(А) 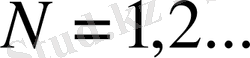болғанда 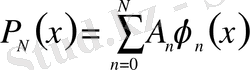түрдегі Фабер-Шаудер жүйесі бойынша
көпмүшелер кеңістігі 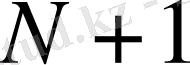өлшемді болады және төмендегідей анықталатын
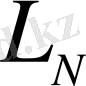кеңістігімен сәйкес келеді:

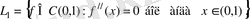
(1.20)

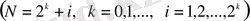
Сонымен қатар Фабер-Шаудер жүйесінің мынадай қасиетін берейік.
(В) Кез келген 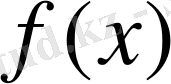функция және 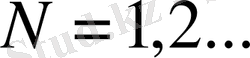үшін коэффициенттері (1.18)
теңдігімен анықталатын, жиынында:
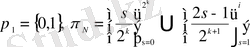(1.21)

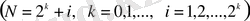
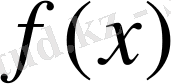-ке сәйкес келетін қосынды

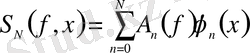
болады.
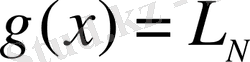функция болғанда болсын. Сонда (А) бойынша -
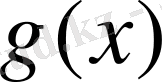жүйесі бойынша көпмүше: 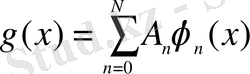және жоғарыда көрсетілгендей ,
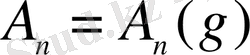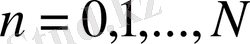болады.
Бірақ болғанда , сондықтан ((1.18) қараңыз) ,
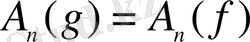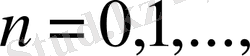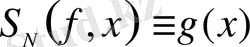яғни болғанда және .
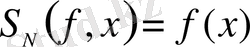(А) және (В) тұжырымдарынан кез келген 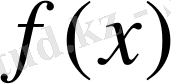үзіліссіз функция үшін
тікелей 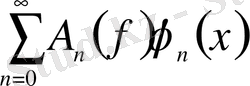қатардың бірқалыпты жинақтылығы шығады. 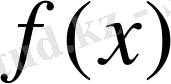-ке жинақталатын
қатардың жалғыздығы алдында тексерілген ((1.17), (1.18) қараңыз). Осылайша
келесі теореманы аламыз.
Теорема 1.1 Фабер-Шаудер жүйесі - 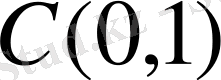кеңістігіндегі базис. Сонымен

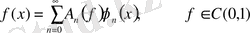
жіктеу коэффициенттері (4) формуласымен анықталады, ал осы жіктеудің
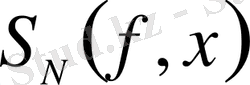дербес қосындылары 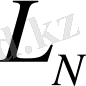кеңістігінде жатады және
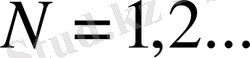болғанда 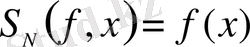(1.22)
қатынасты қанағаттандырады.
Ескерту. Әрбір 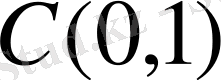кеңістігіндегі ортонормаланған базис -
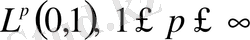кеңістігінде де базис болады. Фабер-Шаудер жүйесінің мысалы көрсеткендей
ортогональдық емес базистер үшін жағдай өзгеше болуы мүмкін. Фабер-Шаудер
жүйесі 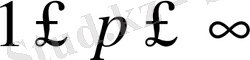болғанда 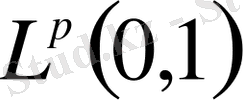кеңістігінде тіпті ең кіші (минималды) емес.
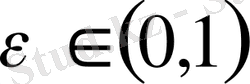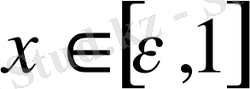Шынында да, әрбір үшін болғанда 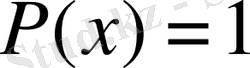және 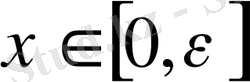болғанда
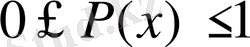болатын 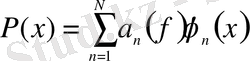көпмүшені оңай құруға болады, демек 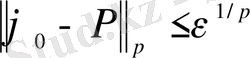болады.
Салдар 1.1 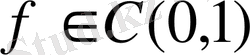болсын. Келесі бағалар орын алады
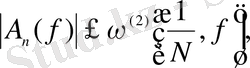
а) 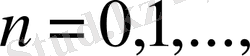мұндағы

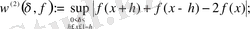
ә) .
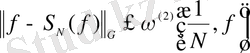Дәлелдеу. а) баға (1.18) формуласынан тікелей шығады. Осыдан кейін
жиынының нүктелері [0,1] кесіндісін интервал ұзындығы 2N-ге
бөледі. Сондықтан ә) баға егер біз 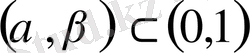интервалының әрқайсысы үшін
,
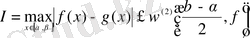мұндағы 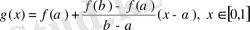екенін тексерсек дәлелденеді.
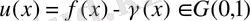болсын. 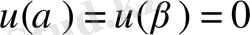екенін ескеріп, 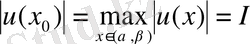болатын 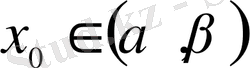нүктесін
табамыз.
Жалпылықты шектемей, 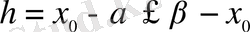деп есептейміз. Сонда 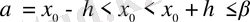, және
.
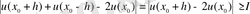Бірақ 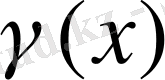функция сызықты, сондықтан 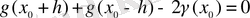, және 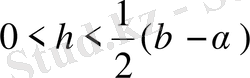екенін ескерсек,

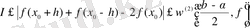
аламыз.
Салдар 1.1 дәлелденді.
Салдар 1.1 а) теңсіздігінен 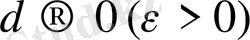болғанда 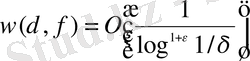болатын әрбір
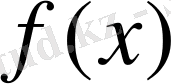функция үшін оның қатары Фабер-Шаудер жүйесі бойынша 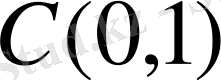норма кеңістігі
үшін абсолютті жинақталады. Сонымен бірге әрбір 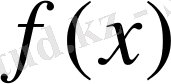үзіліссіз функция
үшін 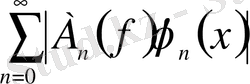қатары бірқалыпты жинақталады. Соңғысы келесі жалпы нәтижеден
шығады.
Теорема 1.2 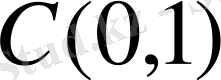кеңістігінде шартсыз базис болмайды.
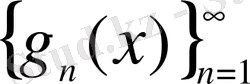
Дәлелдеу. 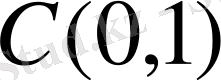кеңістігінде базис болсын және 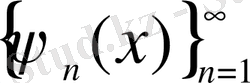- оның
түйіндес жүйесі (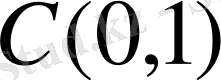-ге түйіндес кеңістік шектелген варияциялар
функциялары кеңістігі болады, сондықтан , 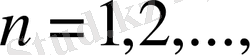сонымен қатар
салдар1.1 қараңыз).
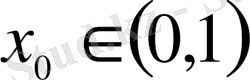нүктені осы нүктеде 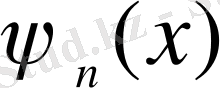, 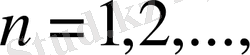барлық функциялары үзіліссіз
болатындай белгілейміз. 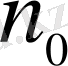- 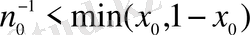болатын натурал сан болсы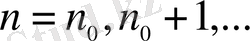н. үшін

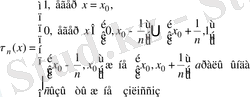(1.23)
қоямыз.
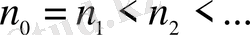(1.24)
әрбір натурал сандар тізбегі үшін (ауыспалы таңбалы қатарлар туралы Лейбниц
теоремасын ескере отырып),
, ,
функциясының бірден аспайтын:
, . (1.25)
кеңістігінде нормасы бар екенін оңай көреміз.
(1.24) түрдегі тізбекті таптық деп ұйғарайық, функциялары
(1.26)
түрде беріледі, мұндағы - жүйесі бойынша қиылыспайтын
көпмүшелер:
.
Сонда, егер болғанда

функциясын қарастырсақ,
мұндағы
болғанда
болады.
Онда (1.25) және (1.26) өрнектерінен
. (1.27)
шығады.
Басқа жағынан, егер болғанда қойсақ, (1.23) және (1.26)
өрнектеріне сәйкес
, . (1.28)
(1.27) және (1.28) бағаларынан 1.2 теоремасынан кеністігінде
шартсыз базис болмайтынын аламыз.
Сол себептен, теорема 1.2 дәлелдеуді аяқтау үшін тізбегін және
(1.24) және (1.26) қатынастарын қанағаттандыратын функцияларын құру
керек. деп алып ( - кеңістігіндегі базис екенін ескере
отырып) және санын көпмүшесі үшін теңсіздігі
орындалатындай таңдап аламыз.
сандары және функциялары құрылды деп есептейік. Сонда
нүктесінде функциясының үзіліссіздігін қолдана отырып, санын
,
мұндағы - кесіндісінде функциясының толық вариациясы
болатындай таңдап аламыз. санын осылай таңдауда
(1.29)
бағалау орын алады.
санын
(1.30)
болатындай таңдап аламыз.
, болады.
(1.29) және (1.30) қатынастарынан шығады. Теорема 1.2 дәлелденді.
Фабер-Шаудер жүйесін қарастыруға оралайық.
Теорема 1.3. болсын. (1.17) қатары функциясының жіктеуі
болуы үшін
, (1.31)
қатынасы орындалуы қажетті және жеткілікті.
Дәлелдеу. Егер , онда салдар 1.1 а) бағасынан тура (1.31) шығады.
Коэффициенттері үшін (1.31) қатынасы орындалатындай, (1.17) түрдегі
қатар берілсін. Сонда бұл қатар абсолютті және бірқалыпты жинақталады,
өйткені болғанда
,
және осыдан қосындысының Ф жүйесі бойынша жіктелуі болады. Сонымен
үшін
. (1.32)
Әрбір және үшін

болатынын белгілейік. Сонымен бірге әрбір үшін , тасушы
функциялары қиылыспайды, онда әрбір үшін қосындысында нөлдік
емес қосылғыштардың саны екіден көп емес. Осы ескертулерді қолдана отырып
және

болатындай санын таңдап аламыз.
(1.32) теңсіздігінен

табамыз.
Теорема 1.3 дәлелденді.
Ескерту. Функция

болатыны оңай көрінеді, дегенмен болатыны айқын. Сайып келгенде
теорема 3 тұжырымы болғанда күшін жояды.
Айнымалыны ауыстыру көмегімен функцияның қасиетін жақсарту туралы
кейбір есептерде пайдалы болатын келесі қорытынды, әрбір функция үшін
айнымалыны ауыстыруды функция Фабер-Шаудер жүйесі бойынша
кемтікті қатар болатындай таңдап алуға болады, яғни
.
Тұжырым 1.2 болсын, и –бүтін сандар тізбегі.
бүтін сандар бар, , , және
болғанда (1.33)
шарты бар функциясы аралығында үзіліссіз Фабер-Шаудер жүйесі
бойынша суперпозициясының жіктеуі
. (1.34)
түрде болады.
Дәлелдеу. (1.18) формуласынан тұжырым 1.2 үшін нүктелерін және
тізбегін құру жеткілікті, осындай
а) , егер , және , егер ;
ә) ;
б) , егер .
Шынында да, осындай нүктелер табылған болса, онда
, ,
біз а) және ә) бойынша -ті бір мәнді кесіндісіне үзіліссіз,
функцияның қатаң бірсарындылығы () болғанға дейін жалғастыра аламыз,
Сонымен б) және (1.18) теңдіктерінен функция қатары (1.34) түрде
болатыны шығады.
Индукция бойынша анықталатын нүктелерін құруда бізге қосымша
келесі шарт орындалатынын қадағалау керек:
в) әр жұп үшін , , не
(I) ,
не
(II) болғанда болатындай интервалы бар болады.
алып, және нүктесін болатындай таңдап аламыз (егер
мүмкін болса, онда кесіндісінде болады, және деп алуға
болады).
нүктелері анықталған деп ұйғарайық, осы нүктелер үшін а), б) және
в) қатынастары орындалсын және - интервалының ең үлкені
болсын. нүктелерін салайық; ол үшін ең алдымен
, (1.35)
болады деп аламыз. нүктелерін салуды екі жағдайға бөлейік.
Жағдай 1.1 немесе қандай да бір , .
Егер жұбы үшін (I) орындалатын болса, онда функциясының
үзіліссіздігін ескере отырып, нүктесін
, . (1.36)
орындалатындай етіп таңдап аламыз. Егер жұбы үшін (II) орындалса,
онда
аламыз.
Жағдай 1.2 Қандай да бір үшін.
Егер болатындай
интервалында нүкте табылатын болса, болады деп жоримыз;
керісінше жағдайда осы интервалда (, немесе ), және біз
аламыз.
Екі жағдайда да
. (1.37)
нүктелер құрылды. Көрсетілген үрдісті жалғастыра отырып,
нүктелерін анықтаймыз. Сонымен қатар болғанда болады. Құрудан
а), б) және в) шарттарының орындалуы (дербес жағдайда (1.35), (1.36)
қараңыз) тікелей шығады. Бұдан басқа әрбір үшін ,
интервалының ең үлкені нүктесімен ұзындықтары аз болатын екі
бөлікке бөлінеді, , онда

болады, яғни б) қатынас сол сияқты орындалды. Тұжырым 1.2 дәлелденді.
Салдар 1.2. болатын екінші ретті суперпозицияның
үзіліссіздігінің интегралдық модулі болатын
болғанда (1.38)
шартын қанағаттандыратын кез келген функция үшін (1.33) түрдегі
функция табылады.
Дәлелдеу. Тұжырым 1.2 бойынша
, ,
әрбір функция үшін (24) баға әділ екенін көрсетсек жеткілікті.
болғанда орындалатынын тексеру оңай.
(- абсолютті тұрақты).
Осыдан қойсақ , біз

аламыз, мұндағы болғанда , осы сияқты болғанда .
Салдар 1.2 дәлелденді.

4. Жалпыланған Фабер-Шаудер жүйелері

1910 жылы Г.Фабер ([43]), 1927 жылы Д.Шаудермен ([48]) қайта ашылған
қазіргі әдебиеттерде Фабер-Шаудер жүйесі атауына ие функция жүйесін
кұрды. (сонымен қатар [23] қараңыз). Үзіліссіз, құрама-сызықтық
функциялардан құрылған бұл жүйе [0,1] кесіндісінде үзіліссіз функциялар
кеңістігінде қарапайым базистің бірі болып табылады. Кейіннен осы жүйе
бойынша функцияларды қатарларға жіктеулерінің әр түрлі қасиеттерін бірқатар
авторлар ([10], [20], [26], [28], [34], [40]) зерттеген.
Осы жұмыста Фабер-Шаудер жүйесін құрайтын Ф{pn} функциялар жүйесінің Ф
жаңа класы енгізіледі.
p0=1, а болатын {pn} натурал сандар тізбегі берілсін.
, деп алсақ, онда әрбір \Q нүкте үшін

, -бүтін жалғыз жіктеу бар болады,
мұндағы , , .
Әрбір бүтін саны
(1.39)
жалғыз түрде беріледі.
, , ,
(1.40)
болатын [0,1] кесіндісінде , функциялар жүйесін анықтайық,
мұндағы n,r,s (1.39) теңдіктен.
\Q жиыны кесіндісінде тығыз орналасқанын қолдана отырып,
функциясын кесіндіде үзіліссіздік бойынша жалғастырайық.
Сол себептен, жүйесі толығымен анықталған және үзіліссіз, құрама-
сызықтық функциялардан тұрады. болғанда функциялар жүйесі
Фабер-Шаудер жүйесімен сәйкес келеді.
жүйесі бойынша:
(1.41)
қатарды қарастырайық және қандай да бір функциясына
кесіндісінің барлық нүктелерінде жинақталады деп ұйғарайық. Онда
коэфициенттері функциясымен бір мәнді анықталады.
Шынында да, (1.40) теңдіктен барлық үшін болғандықтан және
барлық үшін болғандықтан
,
(1.42)
шығады. Осыдан
.
Егер де болса, онда болады ((1.39) қараңыз) және

болатындай үшін
(1.43)
сызықтық теңдеулер жүйесі орындалады.
(5) сызықтық теңдеулер жүйесін жай түрлендірулер келесі теңдеулер
жүйесіне келтіріледі:
(1.44)
(1.45) жүйенің анықтауышы Вандермонд анықтауышы болады және келесі
нөлден өзгеше өрнекке тең болады:
.
Сол себептен, және белгіленген болғанда ,
коэффициенттер (1.44) теңдеулер жүйесінен бір мәнді анықталады.
Теорема 1.4 болсын және жүйесі бойынша қатарға жіктелсін,
яғни
.
Сонда коэффициенттері үшін
. (1.45)
баға орындалады. Мұнда - функциясының үзіліссіздік модулі.
Дәлелдеу. және белгіленген болсын ал .
, , ,

деп белгілейік, сонда жаңа белгілеулерде (1.44) теңдеулер жүйесі келесі
түрге келеді

Берілген жүйенің анықтауышы Вандермонд анықтауышы болады ([25] қараңыз)

және, біздің жағдайда нөлден өзгеше екені айқын.
Сондықтан, берілген сызықтық теңдеулер жүйесінің жалғыз шешімі бар, оны
Крамер формулалары арқылы табуға болады.
анықтауышы j-ші бағаны бос мүшелер бағанына ауыстырылған
анықтауышынан алынған болсын. анықтауышын j баған элементтері бойынша
жіктесек,
,
аламыз, мұндағы - анықтауыш элементтеріне тұратын алгебралық
толықтауыштар.
Осы алгебралық толықтауыштарды қарастырайық.

Мұнда бойынша алынған әр түрлі сандардың
көбейтіндісінің қосындысын білдіреді ([36], 40 бетті қараңыз).
болғандықтан, қосындысындағы әрбір қосылғыш модуль бойынша бірге тең.
қосындысындағы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.