Экстремалды есептерді шешудің геометриялық, алгебралық және вариациялық әдістері


Мазмұны
Кіріспе. 2
1-тарау. Экстремалды есептер.
1. 1 Ежелгі замандағы экстремалды есептер. 4
1. 2 Максимум мен минимумға геометриялық есептер. 10
1. 3 Экстремалды есептерді шешудегі алгебралық әдіс. 15
1. 4 Негізгі теоремаларды қолданып, кейбір есептерді шешу. 17
2-тарау. Экстремалды есептерді шешу тәсілдері.
2. 1 Бір айнымалы функциялардың экстремумын есептеу. 22
2. 2 Ферма теоремасы. 25
3-тарау. Көп айнымалы функциялардың экстремумын есептеу.
3. 1 Лагранж принципі. 28
3. 2 Кейбір есептерді Лагранж принципі бойынша шешу. 34
3. 3 Вариациялық есептеулер және оларға Лагранж принципін 39
қолдану.
Қорытынды. 50
Пайдаланған әдебиеттер. 51
Кіріспе.
Теория мен іс-тәжірибенің әр түрлі мәселесін шешуде ең тиімдіні (оптималдыны) іздеу қажеттілігі туады. Бұл талап толығымен дұрыс, өйткені қолдағы ресурстар әрқашан шектеулі, сондықтан көпке жеткізгін келеді. Бұл туралы орыстың ұлы математигі П. П. Чебышев былай деген: «Тәжірибеде сұрақтардың көбі ең үлкен және ең кіші шамалар есебіне әкеледі, . . . және осындай есепке шешімді біз тәжірибеде барлық жерде ең жақсы, ең тиімдіні іздейтін талабымен қанағаттандырамыз». Осындай есептердің математикалық шешімі кейбір айнымалылардың максимумы мен минимумының (экстремумын) іздеу қажеттілігіне сәйкес келеді. Осыған байланысты мұндай есептерді экстремалды деп атайды. Адамзат пайда болғаннан бергі тарихында осындай есептер мөлшері көп жиналды. Бұл есептерді шешу қажеттілігі оларға шешу әдісін құру қажеттілігін туғызды.
Ертеден бастап адамдар жермен айналысып, оны өлшеуді, тұрғын үй салуды және тағы басқаларға үйренді. Бұның барлығы геометрияның математикалық аппаратын құруды талап етті. Геометриялық әдіс экстремалды есептерді пайымдауда бірінші болды.
Тәжірибе мәселесін шешуде экстремалды есептерді қолдану әрқашан үлкен қызығушылық туғызады. Егер осындай мәселе шешімі оптималды режимді іздеумен байланыстырса ( ресурстарды үнемдеу, технологиялық процесс, үдеу және т. с. с. ), онда математика әдісіне ерекше көңіл бөлу керек болады. Осыған байланысты математика ғылымында экстремалды есептерді шешу әдісін іздеу әрқашан бірінші жоспарға қойылады және бүгінгі күнде математикада осындай есептерді шешу әдісі көп жинақталған.
Сондықтан, дипломдық жұмысымның негізгі мақсаты: кейбір экстремалды есептердің геометриялық әдіспен және қазіргі математика әдісімен шешіп көрсету.
Зерттеу пәні: ежелгі заманда пайда болған және бүгінгі күнде математикадағы экстремалды есептер және оларды шығару әдістері.
Зерттеу объектісі: экстремалды есептерді шешу әдістері.
Геометриялық әдіспен көптеген тамаша экстремалды есептер- Герон есебі, Зенадор жұмысындағы изопериметрлік есеп және тағы басқалары шығарылды. Геометриялық әдіспен шешілген барлық экстремалды есептерге тоқталмаймыз, өйткені бұл әдіс оңай емес. Сондықтан экстремалды есептерді басқа әдіспен шешу қажеттілігі туды.
Бұл әдіс алгебрадан табылды. Мұнда параболаның тамаша дөңестік қасиетін, орта арифметикалық және орта геометриялықты байланыстыратын теңсіздікті қолданып, көп экстремалды есептер шығарылды. Бірақ бұл әдіс те жақсы болған жоқ.
Ғылым мен техниканың дамуы экстремалды есептерді шешудің ортақ әдісін құруды талап етті. Экстремалды есептерді шешудің ортақ әдісі болып Ферма әдісінің Лагранж көбейткіш әдісімен сәйкес келуі жатады. Экстремалды есептер теориясының әрі қарай дамуы Ферма мен Лагранж пікірлеріне сүйеніп жалғасты.
Дипломдық жұмыста экстремалды есептерді шешудің әр түрлі әдістері келтірілді. Бұл жұмыстың негізгі жерлерін атап өтейік:
- Ежелгі заманда пайда болған экстремалды есептер-Герон есебі және изопериметрлік есеп шешімдері келтіріледі.
- Евклидтің, Архимедтің экстремалды есептерін геометриялық әдіспен шешіп көрсетіледі.
- Экстремалды есептерді шешу әдісі алгебралық теңдеу мен теңсіздік қасиеттеріне негізделіп шығарылады.
- Математиканың дамуымен қатар пайда болған Лагранж әдісі арқылы экстремалды есептерді шешуді қарастырылады.
1-тарау. Экстремалды есептер
1. 1 Ежелгі замандағы экстремалды есептер
Математиканың экстремалды есептері ежелгі Грецияда шықты. Барлық уақытта адамның кез келген қарекеті тиімді қылықты таңдау тілеуімен байланысты. Бұған жататындар, мысалы, қолда бар ресурстармен өзіне ең үлкен ауданды қоршап алу қажеттілігі, базарда тиімді бәсеке сауда өткізу, жайлы тұрғын үй салу және т. б. Тәжірибе қарекетінде адам геометрияны көп қолданғандықтан, бірінші есептер геометриямен байланысты.
Экстремалды есептер кездесетін әдеби шығармалардың бірі - Ежелгі Римнің (б. э. д. 9ғ) ұлы ақыны П. В. Маронның «Эненда» шығармасы.
Бұл шығармада бірінші рет әдеби тілмен қазіргі кездегі «Изопериметрлік есеп» немесе «Дидона есебі» мәселесі суреттеледі. Берілген ұзындығы бар жазық, тұйықталған қисық арасынан максималды ауданды қисықты табуға болады.
«Эненда» кітабында үйінен қуылған Финикеяның ханымы Дидона Тир қаласының тұрғындарынан құрылған аздаған отрядпен ағасынан қашып, Жерорта теңізінің жағалауымен батысқа корабьмен кетіп қалады. Ол Тунис шығанағын таңдап, сол жерге қоныстанады да, ондағы тузилерден: «өгіз терісімен қанша жерді қоршай алсам, сонша жерді сатып алайын» -деп шарт қояды. Келісімге келгесін, Дидона өгіз терісін ұзынынан жіңішке етіп кесіп, белбеу жасап, жерді қоршаған соң, сол жерге Карфаген қаласын салғызады. Дидона мүмкін берілген ұзындығы бар жазық түзулер, шеңбер қарастырылып отырған жағдайда жарты шеңбер ең үлкен ауданды болатынын білген болар.
Изопериметрлік есептерді шешу ежелгі гректерге белгілі болды. Архимед(б. э. д. 2ғ. ), Зенадор(б. э. д. 3, 1ғ. ) бұл есептің шешімін жеткілікті қатаң өткізді.
Бұл есептердің шешімі А. Герон (б. э. д. 1ғ. ) есебіне негізделген, бірақ бұл шешім Геронға дейін белгілі болған. Есеп Геронның «Айна туралы» кітабына енгізілген. Кітаптың атынан есептің айнаға қатысы бар екенін, нақтырақ айтқанда, сәуленің айна арқылы өтуі туралы екенін көре аламыз.
Герон есебі: А және В нүктелері ℓ-мен шектелген бір жарты жазықтықта жатыр. А-дан Д-ға дейінгі В-дан Д-ға дейінгі арақашықтық қосындысы ең аз болатындай, ℓ түзуінен Д нүктесін табу керек. (1-сурет. )
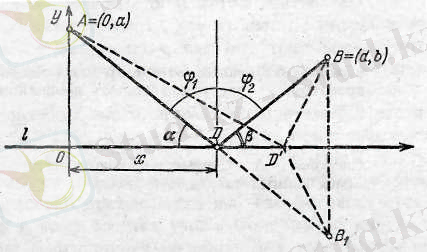 1- сурет.
1- сурет.
Шешуі: Есепті шешу үшін ℓ түзуіне қатысты В нүктесіне симметриялы В 1 нүктесін саламыз.
АВ
1
кесіндісінің ℓ түзуімен қиылысуын Д нүктесі деп белгілейміз. Д ізделінді нүкте екенін көрсетеміз. Ол үшін басқа Д
1
 ℓ нүктесін қарастырамыз. Онда ΔАВ
1
Д
1
-ден
ℓ нүктесін қарастырамыз. Онда ΔАВ
1
Д
1
-ден

АД 1 +Д 1 В 1 >АВ 1
мұнда АВ 1 =АД+ДВ В 1 Д 1 =ВД 1 болғандықтан
АД 1 +Д 1 В > АД+ДВ
шығады, яғни Д ізделінді нүкте.
Бұл есептің шешімі ертедегі ғылымда оптиканың есептерін шығаруға мүмкіндік беретін жаңалық ашылғандай жоғары бағаланды. Дербес жағдайда оптиканың белгілі заңы: «сәуленің сыну бұрышы шағылу бұрышына тең» суреттен оңай көрініп тұр. Герон есебін қолданып, келесі есептерді шығаруға болады.
1. Бұрыш және оның ішінде С нүктесі берілген. АВС үшбұрышының периметрі ең үлкен болатындай үшбұрыштың қабырғаларынан А және В нүктелерін тап.
2. Бұрыш және оның ішінде С және Д екі нүктелері берілген. СА+АВ+ВД ұзындығының қосындысы ең кіші болатындай бұрыштың қабырғаларынан А және В нүктелерін тап.
Енді Дидон есебін шешуге кірісейік. Зенадорға изопериетрлік есепті шешудің негізгі жолы белгілі болды. Оның жұмысының негізгі ойын қарастырайық. Алдмен изопериметрлік фигуралар, максималды n-бұрыш терминдерін атап өтейік. Периметрі бірдей фигураны изопериметрлік фигура деп атайды. Барлық изопериметрлік арасынан ең үлкен ауданды жазық n-бұрыш максималды n-бұрыш деп аталады.
Зенадор теоремасын қарастырмастан бұрын келесі үш лемманы қарастырайық.
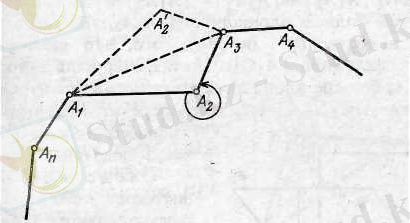 2-сурет.
2-сурет.
1-лемма: Дөңес емес көпбұрыш максималды бола алмайды. (2-сурет. )
Дәлелдеу: Дөңес емес жазық n-бұрышты қарастырайық.
А 1 А 2 . . . А n көпбұрышының А 2 биіктігі фигураның ішінде орналассын, яғни А 1 А 2 А 3 бұрышы 180º үлкен. А 1 А 3 кесіндісіне қатысты А 2 нүктесіне симметриялы А ' 2 нүктесін саламыз.
А 1 А 2 . . . А n және А 1 А' 2 . . . А n көпбұрыш бірдей периметрлі, бірақ А 1 А' 2 . . . А n ауданы А 1 А 2 . . . А n көпбұрыш ауданынан үлкен. Осыдан максималды көпбұрыш дөңес болуы керек.
Ескерту . 1-леммадағы дөңес фигура туралы тұжырымды Зенадор айтпай кетсе де, бұл тұжырым берілді.
2-лемма: Максималды n-бұрыш тең қабырғалы болу керек. (3-сурет. )
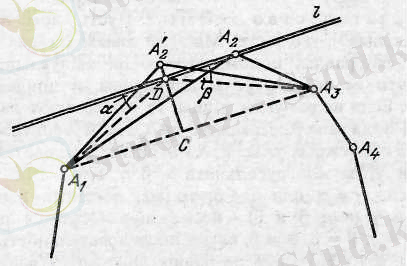 3-сурет.
3-сурет.
Дәлелдеу:
А
1
А
2
. . . А
n
максималды n-бұрыш болсын. Онда ол 1-лемма бойынша дөңес болады. Әрі қарай талдауды «қарсыдан» жорамыз. Мысалы, А
1
А
2
≠А
2
А
3
болсын, яғни көпбұрыш тең қабырғалы емес. ℓ А
1
А
3
болатындай етіп, А
2
биіктігі арқылы ℓ түзуін жүргіземіз. Онда Герон есебін шешу нәтижесін ℓ түзу мен А
1
А
3
нүктесіне қолданып Д
 ℓ нүктесін аламыз, ондағы А
1
Д+ДА
3
қосындысы минималды болады. Осыдан
ℓ нүктесін аламыз, ондағы А
1
Д+ДА
3
қосындысы минималды болады. Осыдан
 А
1
ДК
1
=
А
1
ДК
1
=
 Equation. 3 А
3
ДК
2
. ℓ және А
1
А
3
параллель түзулерінде
Equation. 3 А
3
ДК
2
. ℓ және А
1
А
3
параллель түзулерінде
 ДА
1
А
3
=
ДА
1
А
3
=
 Equation. 3 А
1
ДК
1
ішкі айқас бұрыштар сиықты. Осыдан,
Equation. 3 А
1
ДК
1
ішкі айқас бұрыштар сиықты. Осыдан,
 А
1
ДА
3
теңбүйірлі, Д≠А
2
. Осы жерде:
А
1
ДА
3
теңбүйірлі, Д≠А
2
. Осы жерде:
Біріншіден, S ΔАДА =S ΔААА осы үшбұрыштардың табаны мен биіктігінің ұзындығы бірдей.
Екіншіден, А 1 Д+ДА 3 <А 1 А 2 +А 2 А 3 Герон есебінен Д≠А 2 нүктесі шешімі ретінде табылады.
ΔА 1 А' 2 А 3 тең бүйірлі үшбұрыш саламыз, ол үшін А 1 А' 2 +А' 2 А 3 =А 1 А 3 +А 2 А 3 . Осыдан А 1 А' 2 >А 1 Д, сондықтан СА' 2 СД биіктігінен үлкен, алайда осыдан А 1 А' 2 . . . А n көпбұрышының ауданы А 1 А 2 . . . А n изопериметрлік көпбұрыш ауданынан үлкен. А 1 А 2 . . . А n максималды n-бұрышқа қайшы. Осыдан А 1 А 2 ≠А 2 А 3 туралы болжам дұрыс емес, сондықтан максималды n-бұрыш тең қабырғалы болады.
Салдар . 2-лемма тұжырымынан:
1. Максималды ұшбұрыш тең қабырғалы болады.
2. Ромб, квадрат максималды төртбұрышты болу керек. Алайда квадрат максималды төртбұрыш болатынын оңай көруге болады. Осыдан бір қабырғасының теңдігі n-бұрыштың максималды болуына жеткілікіз.
3-лемма . Максималды n-бұрыш тең қабырғалы болуы керек.
Бұл лемма Герон есебінің шешуіне сүйене отырып дәлелденеді.
Осы үш леммаға сүйеніп, Зенадор теоремасының қазіргі құрылымын келтірейік.
Зенадор теоремасы. Егер барлық n-бұрыштар арасында периметрі берілген ең үлкен ауданы бар жазық n-бұрыш бар болса, онда ол тең қабырғалы және тең бұрышты болуы керек.
Осы теоремадан максималды жазық n-бұрыштың бар болу шарты бар. Бар болу сұрағының мәні және бар болуға сәйкес теореманы дәлелдеу әдісі тек 19 ғасыр аяғында түсінікті болды, сондықтан Зенадор үшін осындай максималды n-бұрыштың бар болуы мүмкін болады.
К. Бейерштрас (19ғ. ) жұмысында құрылған математикалық аппараттан шығатын дәлелдеусіз лемманы, дербес жағдайда компакты көпмүшеде берілген ең үлкен мәнді үзіліссіз бейнелеудің бар болу теоремасын келтірейік.
4-лемма. Максималды n-бұрыш бар болады.
Сондықтан Зенадор теоремасын келесі түрде қарастырайық.
2-лемма. Максималды n-бұрыш дөңес n-бұрыш болады.
Дұрыс n-бұрыш, p-периметр, S-оның ауданы, а-n-бұрыштың қабырғаларының ұзындығы, R, r- дөңгелектің сәйкес іштей және сырттай радиусын қарастырайық. Онда мынаны аламыз:
a=2Rsin
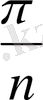 , r=Rcos
, r=Rcos
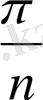 ,
,
P=2nRsin
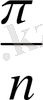 , S=
, S=
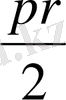
Сондықтан
P
2
-4n tg
 (1)
(1)
(2) теоремадағы кейбір кез келген n-бұрыштың p-периметрі, S-оның ауданы болса, онда P
2
-4n tg
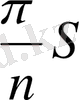 ≥0 (2)
≥0 (2)
теңдігі орындалады. (2)
 P
2
≥4n tg
P
2
≥4n tg
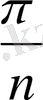 S
S
Cондықтан tg
 ≥
≥
 теңсіздігі 0≤
теңсіздігі 0≤
 <
<
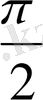 үшін дұрыс, осыдан
үшін дұрыс, осыдан
P
2
≥4n tg
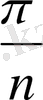 S≥4n
S≥4n
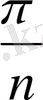 S=4
S=4
 S
S
шығады, яғни P
2
-4
 S≥0 (3)
S≥0 (3)
теңсіздігі дұрыс. Кез келген дөңгелекке
P
2
-4
 =0 (4)
=0 (4)
теңдігі орындалатынын көреміз, мұндағы P- дөңгелек ұзындығы, S- шеңбер ауданы.
Енді кез келген жазық, тұйық P* ұзындықты қисықты қарастырайық. Француз математигі К. Жорданно (19ғ) еңбегінің нәтижесін қолданып, келесі лемманы аламыз.
5-лемма.
S ауданын қамтитын кез келген жазық, тұйық P* ұзындықты қисық және кез келген
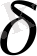 >0 үшін n-бұрышты, p- периметрді, S-ауданды табуға болады, олар келесі теңсіздікті
>0 үшін n-бұрышты, p- периметрді, S-ауданды табуға болады, олар келесі теңсіздікті
P-P*≤
 , S-S*≤
, S-S*≤
 (5)
(5)
қанағаттандырады.
(3) теңсіздік пен 5-лемманы қолданып, кез келген
 >0 саны үшін p периметрлі және S ауданды көпбұрыш аудан табылатынын көреміз.
>0 саны үшін p периметрлі және S ауданды көпбұрыш аудан табылатынын көреміз.
4
 S*≤4
S*≤4
 S+4
S+4
 ≤P
2
+4
≤P
2
+4
 ≤(P*+
≤(P*+
 )
2
+4
)
2
+4

Сондықтан, кез келген
 көмегімен
көмегімен
4
 S*≤(P*)
2
(6)
S*≤(P*)
2
(6)
теңдігін аламыз.
Ол (4) бойынша дөңгелек жайындағы теңсіздікке өзгереді. Осыдан біз изопериметрлік есептің толық шушімін беретін тұжырымға келеміз.
3-теорема . Кез келген тұйық, ұзындығы берілген қисықты аудан, дөңгелектің ұзындығы осындай шеңбер ауданынан басым емес.
1. 2 Максимум мен минимумға геометриялық есеп
Жоғарыда біз математиканың маңызды бір мәселесі - изоперметрлік есептерді шешудің геометриялық әдісін қарастырайық. Мұнда біз геометрияның кейбір басқа экстремалды есептерін қарастырамыз.
Геометриядағы экстремалды есептердің мәнін атап өту үшін, қарапайым математикалық мәселені шешуде экстремалды есептерді шешу негізгі болатынын көрсететін мысалдар математика тарихында көп кездеседі. (мұнда көбіне геометриялық есеп) . «Жарық сәулесінің парабола фокусында қалай жинайтын» Архимед шешкен есепті мысал ретінде алуға болады(өзінің туған қаласы Сиракузаны жаудан қорғауда) . Бұл есептің шешімі Герон есебінің шешіміне сүйенеді.
Геометрия экстремалды есептердің әр түрлі қойылымына бай. Бұл жерде тек антик математиктері - Евклид, Архимед есептерін қарастырамыз.
Евклидтің «Бастама» (б. э. д. 4ғ. ) кітабында максимумға тек бір ғана есеп берілген. Енді соны қарастырайық.
Евклид есебі. Берілген АВС ұшбұрышына ең үлкен ауданды ADEF (EFAB, DEAC) параллелограмын іштей сызу керек. (4-сурет. )
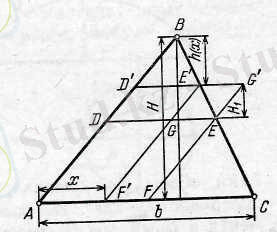 4- сурет.
4- сурет.
Шешуі: Евклидтің «Бастамасында» берілген осы есептің шешімін келтірейік. Ізделінді ADEF параллелограммының D, E, F биіктіктері АВ, ВС, АС сәйкес қабырғаларының ортасы болатынын дәлелдейік .
ABEF-тан өзгеше АВС ұшбұрышына іштей сызылған AD′E′F′ параллелограмын қарастырайық. G′=D′E′∩EF, G=DE∩E′ F′ деп белгілейміз. AD′E′F′ параллелограмм ауданы ADEF параллелограмм ауданынан EG′E′G параллелограмм аудан шамасына кіші екенін көрсетейік. H, H′ арқылы сәйкесінше В және Е′ нүктелері арқылы жүргізілген ∆АВС, ∆GE′E биіктік ұзындығын, ал b арқылы АС ұзындығын белгілейік.
∆GE′E және ∆АВС ұқсастығынан
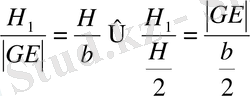
шығады. Осыдан
S
D
′
GED
=
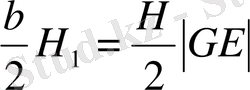
шығады. Демек
S ADEF =S ADGF +S FGEF =S ADGF +S DGED =S ADGEGF =S ADEF +S GEG
Яғни
S
ADEF
=
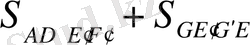
және сондықтан
S ADEF >S ADEF
Архимед (б. э. д. 287-212жыл) «Шар және цилиндр туралы» шығармасында келесі есепті шешеді.
Архимед есебі. Сфералық шар бетінің берілген ауданы бар, барлық сегмент арасында максималды көлем сыятындай шар сегментін тап.
Шешуі: Архимед бұл есепті шешкенде келесі шешімге келді: «бірдей бетпен шектелген барлық сфералық сегметтер арасынан жарты шар ең үлкен болады». Қазіргі кезде Архимедтің осы сөздерінің құрылымы келесі түрде беріледі: Беттің берілген шамасы бар барлық шар сегменті арасынан көлемі жағынан ең үлкен жарты шар болаады. Осы шешімді дәлелдейік. (5-сурет)
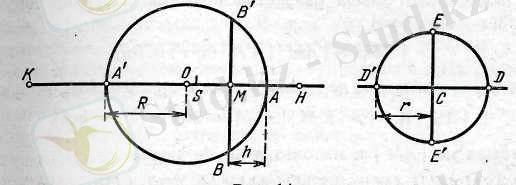 5-сурет.
5-сурет.
R-радиусы бар, АА′- кез келген шардың диаметрі болсын. А′А түзуі бойынан конус биіктігі HМ және АВ табанының радиусының көлемі ВАВ′ сегментіндей болатындай етіп, ОH кесіндісін кейінге қалдырамыз. ОА′ кесіндісінің жалғасынан А′К кесіндісін А′К=R болатындай етіп, кейінге қалдырымыз.
Конустың көлемі (V к ) келесі формуламен есептеледі:
V
k
=
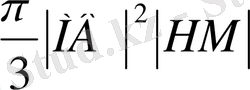
ВАВ′ шар сегментінің көлемі (V c ) келесі формуламен есептеледі:
V
c
=
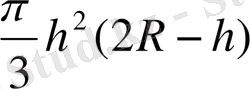 мұндағы h=MA
мұндағы h=MA
Белгілі
МВ 2 =A′MMA (7)
теңдік көмегіен және V k =V c болжамынан мынаны аламыз.
V
k
=
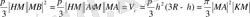 (8)
(8)
Осыдан
МА 2 КМ=MB 2 HM (9)
HMA′MMA=МА 2 КМ (10)
аламыз.
(10)
 HMA′M=MAKM шығады, яғни
HMA′M=MAKM шығады, яғни
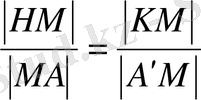 (11)
(11)
Әрі қарай S жш жарты шар және S с сегмент аудандарының формуласын жазамыз:
S жш =2πr 2 , S c = 2πRh
мұндағы r- ізделінді жарты сфераның радиусы. Онда
ED=
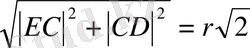 (12)
(12)
AB 2 = AA′AM (13)
теңдігі белгілі.
Сондықтан (12), (13) -ден S жш =S c теңдігі бойынша
πAB 2 =πAA′AM=2πRh=S c =S жш =2πr 2 =πED 2
аламыз. Демек,
АВ=ED (14)
Әрі қарай AS=CD=r кесіндісін кейінге қалдырып, белгілі деректі қолданамыз: екі бірдей периметрлі кіші қабырғасының ұзындығы үлкен болса, онда сол бұрыштың ауданы үлкен болады, яғни егер х, у және х 1 , у 1 тік бұрыш қабырғаларының ұзындықтары, 2х+2у= 2x 1 +2y 1 , y<x, y 1 <x 1 , y<y 1 , онда ху<х 1 у 1 (15)
A′S+SA=2R=A′MMA болатыны айқын. Сондықтан (15)

А′S×SA>A′M×MA
немесе осыдан
(2R-r) >(2R-h) h (16)
аламыз.
Сосын, сегменттің бүйір беті мен жарты теңдіктерінен 2πr
2
=2πRh
 r
2
=Rh
r
2
=Rh
аламыз, яғни (17)
АS 2 =A′K×MA
(16) және (17) қосып,
A′SSA+AS 2 >A′MMA+A′KMA
аламыз немесе осыдан
AS×(SA+A′S) >MA×(A′M+A′K)
шығады.
Бірақ SA+A′S=2R, A′M+A′K=3R-h, сондықтан соңғы теңсіздік келесі түрде болады:
r×2R>h(2R-h) (18)
(18) теңсіздігін АМ=h-қа көбейтіп,
2Rrh>(3R-h) h 2 (19)
аламыз.
V- арқылы ізделінді жарты шардың көлемін белгілейміз, сонда
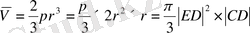
Демек,
CD=AS=r, ED 2 =AA′×AM
онда
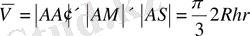
Әрі қарай (19) теңсіздікті қолданып
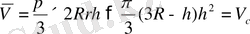
аламыз, сонымен
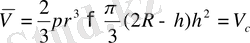
яғни жарты шар көлемі шар сегментінің көлемінен үлкен.
Осы дәлелдеуде қолданылған конустың, шардың шар сегментінің көлемі, шар беті-ауданы, сегметтің сфералық бетінің формулаларын ең бірінші рет Архимедпен ашылды.
1. 3 Экстремалды есептерді шешеудегі алгебралық әдіс
Жоғарыда ежелгі заманнан бері адамға белгілі экстремалды есептерді шешу әдісінің геометриялық талдауы қарастырылды. Бұл әдіс оңай болғанымен де оны осындай есептерді шешудегі қарапайым және ортақ әдіс деп есептей алмаймыз.
Келесі кезекте экстремалды есептерді шешу әдісі болып алгебралық теңдеу мен теңсіздіктің қасиеттеріне негізделген әдіс табылады. Біз квадрат үшмүшенің дөңестік қасиетіне негізделген және орта арифметикалық пен орта геометриялық оң сандарды байланыстыратын теңсіздікті қолдануда кейбір экстремалды есептерді шешу әдісін қарастырамыз.
Квадрат үшмүшені қарастырайық.
y= ax 2 +bx+c, a≠0 (20)
оны
y=ax
2
+bx+c= a(x+
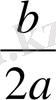 )
2
+
)
2
+
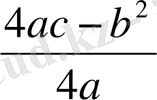 (21)
(21)
түріне келтіреміз.
Осыдан келесі теореманы аламыз:
1-теорема.
1) Егер а>0 болса, онда у=ax
2
+bx+c өрнегі х=-
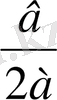 және у
min
=
және у
min
=
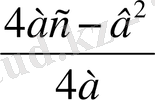 болғанда минимумға жетеді.
болғанда минимумға жетеді.
2) Егер а<0 болса, онда y=ax
2
+bx+c өрнегі х=-
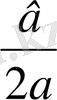 және у
max
=
және у
max
=
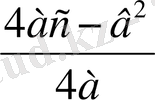 болғанда максимумға жетеді.
болғанда максимумға жетеді.
Келесі екінші теореманы қарастырайық.
2-теорема. Геометриялық ортаның n-оң х 1 , х 2 , . . . х n сандары олардың орта арифметикалық
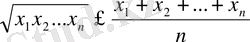 (22)
(22)
санынан үлкен емес.
Теңдік белгісі бұл жерде х 1 , х 2 , . ., х n сандары
х 1 =х 2 =…=х n (23)
бір-біріне тең болғанда қойылады. Көп қызықты есептер кездеседі, дербес жағдайда экстремалды есептердегі қосындысы х 1 +х 2 + . . . +х n =c=const немесе көбейтіндісі х 1 ×х 2 × . . . ×х n =c=const, мұндағы х i >0, i=1, …, n. Осындай есепті шешу үшін келесі екі теорема қажет болады.
3-теорема
. Егер х
1
, х
2
, . . . х
n
оң сандарының қосындысы тұрақты және х
1
+х
2
+ . . . +х
n
=c=const болса, онда олардың көбейтіндісі P=x
1
, x
2
, …, x
n
ең үлкен мәнге x
1
=x
2
=…=x
n
=
 жағдайына жетеді.
жағдайына жетеді.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz