Блоктік шифрлеу

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Блоктік шифрлеу

Қызіргі кезде қолданылатын симметриялы блоктік шифрлеу алгоритмі «Файстельдің блоктік шыфры» атты структурасында негізделген. Соған байланысты Файстель шифрі құрылған принциптерді түсіну маңызды. Біз потоктік және блоктік шифрді салыстырып, Файстель шифрінің құрылуын қарастырамыз. Ал содан кейін сәйкес алгоритмді практикалық іске асына да тоқталамыз.

Потоктік және блоктік шифрлеу

Потоктік шифрлер деп цифрлік берілгендер кезекпен, яғни биттен кейін бит немесе байттан кейін байт шифрленетін шифр түрін айтамыз. Классикалық потоктік шифрлерге Виженер (кілтті автоматты таңдаумен) және Вернам шифрлері мысал болады.

Блоктік шифр деп шифрлеудің логикалық бірлігі ашық текстің кейбір блогы болатын шифрді айтамыз. Оны қайта қалпына келтіру кезінде дәл сол ұзындықты шифрленген текст блогы алынады. Әдетте өлшемі 64 битті блоктар қолданылады. Шифрлеудің кейбір режимдерінде потоктік сияқты эффективті болады.

Блоктік шифрлер жақсы зерттелген. Потоктік шифрлерге қарағанда олар көп қолданылады. Традиционды шифрлеу схемасы қолданылатын көптеген желілік қосымшаларда блоктік шифрлер қолданылады.

Файстель шифрін құру подстановкасы

Блоктік шифр ашық текстің n-биттік блогының сондай-ақ өлшемді шифрленген текст блогына түрленуі мүмкін.

Түрлі блоктардың саны 2 ⁿ -не тең, және шифрлеу қайтарымды (яғни дешифрленетін) болуы үшін сондай блоктардың әрқайсысы өзінің шифрленген текстің уникалды блогына түрлендіріледі. Бұндай түрлендіру қайтарымды немесе сингулярлы емес деп аталады. n=2 үшін сингулярлы және сингулярлы емес түрлендірулерге мысал.

Көрінетін көрініс Көрінбейтін көрініс

Ашық текст Шифрленген текст Ашық текст Шифрленген текст

00 11 00 11

01 10 01 10

10 00 10 01

11 01 11 01

Көрсетілген мысалда қайтарылмайтын көрініс жағдайында 01 шифрленген тексті ашық текстің 2 түрлі блогына сәйкес келеді. Егер тек қайтарылатын көріністермен шектелсек, түрлі мүмкін түрлендірулер саны 2 ⁿ ! -ге тең болады.

3. 4. суретінде n=4 үшін подстановтік шифрдің жалпы схемасы көрсетілген. Кіріске түсетін 4-биттік мәндер 16 мүмкін болатын бастапқы жағдайдың біреуін анықтайды. Бұл жағдай 16 уникалды соңғы жағдайдың біреуіне подстановтік шифр ретінде көрінеді. Уникалды соңғы жағдайдың әрқайсысы шифрленген текстің 4-биттік мағынасын білдіреді. Шифрлеу және дешифрлеу схемасын таблица түрінде көрсетуге болады (3. 1) . бұл блоктік шифрлеу процесінің жалпы схемасы және ол кез келген ашық және шифрленген тексті өңдеу үшін қолданылады.

4-биттік енгізу

3. 4. сурет (n=4 жағдайындағы) n - биттік блоктардың блоктік подстановкасының жалпы схемасы

Таблица 3. 1. 3. 4. суретінде көрсетілген подстановтік шифр үшін шифрлеу және дешифрлеу таблицасы

Ашық текст Шифрленген текст Ашық текст Шифрленген текст

1110 1110

0001 0100 0001 0011

0010 1101 0010 0100

0011 0001 0011 1000

0100 0010 0100 0001

0101 0101 1100

0110 1011 0110 1010

0111 1000 0111

1000 0011 1000 0111

1001 1010 1001 1101

1010 0110 1010 1001

1011 1100 1011 0110

1100 0101 1100 1011

1101 1001 1101 0010

1110 1110

0111 0101

Алайда берілген подходты практикалық іске асыру кезінде келесі проблема туындайды. егер үлкен емес өлшемді блокті қолдансақ, мысалы n=4, жүйе классикалық подстановтік шифрге эквивалентті болады. Біз көргендей, бұндай жүйелер осал және ашық текстің сатистикалық анализі арқылы ашылуы мүмкін. Бұл жетіспеушілік қайтарылатын шифрден емес, қысқа блоктарды қолданудан туындайды. n-ның үлкен мәндерінде және ашықтексті шифрленгенге келтіретін алғашқы ашық текстің статистикалық характеристикасы жақсы әшкерленуі соншалықты, бұндай түрлі криптоанализ қажетсіз болады.

Алайда үлкен өлшемді блокті кез келген қайтарылатын подстановкалардың мүмкіндігі алгоритмді іске асыруда және сәйкес қосымшаның орындалу жылдамдығы тұрғысында тұрақсыз. Бұндай түрлендіру үшін кілт ол көрініс болады. Қайтадан ашық текст кеңістігінің нақты қайтарылатын көрінісін n=4 үшін шифрленген кеңістікте анықталуын көрсететін 3. 1 кестесіне назар аударсақ. Көріністі сәйкес ашық текст мәндері үшін шифрленген текст мәндері көрсетілген кестенің 2-ші бағанындағы элементтермен беруге болады. Бұл негізінен берілген нақты көріністі барлық басқа мүмкін болатын көріністерден ерекшелейтін кілт болып табылады. Біздің жағдайда кілт ұзындығы 64-ке тең. әдетте n биттік подстановтік блоктік шифр үшін кілт өлшемі n x 2 ⁿ -ге тең. Егер блок 64-биттік өлшемді болса (бұндай өлшемді шифр статистикалық анализ көмегімен жүргізілетін бұзуларға жақсы қарсы тұра алды), онда кілт өлшемі 64х2 ⁶⁴ =2 ⁷⁰ =10 ²¹ битке тең.

Бар проблемены зерттей отырып, Файстель үлкен n үшін бұндай блоктік шифрлеудің идеалды жүйесін іске асыратын жай компоненттер жиынтығымен [FEIS75] аппроксимациялауды ұсынды. Файстельдің ұсынысын талқылаудан бұрын, назарларыңызды келесіге аударсақ. Біз блоктік подстановтік шифрдің жалпы түрімен жұмыс істей алмаймыз, бірақ, сәйкес алгоритмді программалық методпен іске асыру үшін, барлық 2 ⁿ ! мүмкін болатын көріністер орнына кейбір тар подмножестваларды қарастыруға болады. Мысалға, біздің көріністер сызықты теңестіру жүйесімен беріледі. n=4 үшін біз мынаны аламыз.

Y ₁ =k ₁₁ x ₁ +k ₁₂ x ₂ +k ₁₃ x ₃ +k ₁₄ x ₄

Y ₂ =k ₂₁ x ₁ +k ₂₂ x ₂ +k ₂₃ x ₃ +k ₂₄ x ₄

Y ₃ =k ₃₁ x ₁ +k ₃₂ x ₂ +k _33x3 +k ₃₄ x ₄

Y ₄ =k ₄₁ x1+k ₄₂ x ₂ +k ₄₃ x ₃ +k ₄₄ x ₄

Бұндағы x _i -ашық текст блогының төрт екілік цифрын, y _i - шифрленген текст блогының төрт екілік цифрін, k _ij - екілік коэффиценттер, ал барлық арифметикалық операциялар 2 модулі бойынша орындалады. Кілт ұзындығы n ² -ге тең, және берілген жағдайда ол барлығы 16 бит. Мәселенің қауіптілігі формулалардың көріністерінде, егер бұндай алгоритм құрылымы криптоаналитикке белгілі болған жағдайда, жүйе осал болуы мүмкін. Берілген мысалда шифрлеу жүйесі негізінен Хилл шифріне эквивалентті, бірақ текстік символдарға емес, екілік мәліметтерге қолданылады.

Файстель шифры

Файстель өзінің [FEIS73] жұмысында подстановкалы шифрді кем дегенде екі базалық шифрдің реттік қолданыста құрылатын, алынған нәтиже осы базалық шифрлердің әрқайсысымен салыстырғанда қатаң болатын продукционды шифрлермен аппроксимациялауды ұсынды. Әдетте, Файстель кезек кезекпен орындалатын подстановка да, перестановка да қолданылатын шифрді ұсынды. Осы ұсыныс Клод Шеннонның (Claude Shannon) диффузия мен конфузия функциялары кезекпен қолданылатын продукционды шифрді құру идеясының практикалық қолданысы болып табылады. Ең алдымен диффузия мен конфузия ұғымдарына тоқталып кетейік, ал кейінірек Файстель шифріне тағы да тоқталамыз. Бірақ, ескере кететін бір факт: 1945ж. айтылып кеткен Шеннонның идеясына негізделген ширек ғасыр бұрын құрылған Файстель шифрінің структурасы қазіргі таңда осы структура негізінде құрылған бүкіл блоктік шифрлеудің симметриялы схемалары болып табылады.

Файстель шифрінің структурасы

3. 5. суретте Файстель ұсынған шифрдің структурасы көрсетілген. Шифрлеу алгоритмінің кірісіне ұзындығы 2w битті және K кілтті ашық тексттің блогы беріледі. Ашық тексттің блогы обработканың n раундтары арқылы кезекпен өтетін, кейін тиісті ұзындықтағы шифрленген тексттің блогын қайта алу үшін қолданылатын екі бірдей бөлікке бөлінеді: L және R . Өткен раундтың шығысында алынған i раунды үшін кіріс ақпараты ретінде L 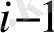және R 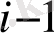жалпы К кілті арқылы есептелген және 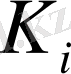құрамды кілт қызмет атқарады. Ереже бойынша, барлық 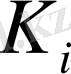құрамды кілттер К жалпы кілтінен сияқты бір-бірінен де ерекшеленеді.

Барлық өңдеу раундтарының схемалары бірдей болып келеді. Ақпараттық блоктың сол жағына ең алдымен подстановка операциясы орындалады. Ол F раундының кейбір функциялары және XOR операциясының көмегімен ақпарат блогының сол жағынан алынған нәтижелердің қосындылары ақпарат блогының оң жағына қолданғанда алынады. Раундтың функциясына барлық раундтардағыдай бірдей структура қолданылады, бірақ раундтың 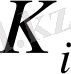құрамды кілт параметрінен тәуелді болады. Подстановкадан кейін ақпарат блогының екі бөлігінің орын ауыстыруын қамтамасыз ететін перестановка орындалады. Жалпы осы структура Шеннон ұсынған подстановкалы-перестановкалы схеманың (SPN - substitution-permulation network) жеке жағдайы болып табылады.

Файстель схемасының практикалық реализациясы келесі параметрлердің мәндерін таңдаудан және конструктивті ерешеліктерден тәуелді.

Блоктың өлшемі. Блоктың өлшемі үлкен болған сайын, соғұрлым шифрдің сенімділігі жоғары болады, бірақ шифрлеу және дешифрлеу операцияларының орындалуының жылдамдығы төмендейді. Қазіргі таңда барлық блоктық шифрлеуге универсалды болатын 64 битті блок өлшемі ең жақсы шешім болып табылады.
Кілттің өлшемі. Кілт ұзын болған сайын, шифр сенімділігі жоғары болады, кілттің ұзындығы өте ұзын болғаны шифрлеу мен дешифрлеу операцияларының орындалуы өте баяу болуына әкеп соқтырады. Қазіргі таңда 64 битті және одан да кіші кілттер сенімсіз болып табылады - әдетте 128-битті кілттер қолданылады.
Өңдеудің раундтар саны. Файстель шифрі идеясының мәні, ақпараттарды өңдеудің бір раундында жоғары сенімділік қамтамасыз етілмейді, бірақ шифрдің сенімділік дәрежесі өңдеудің әр жаңа раундында жоғарылайды. Әдетте, 16-ға тең раундтар санын таңдайды.
Құрамды кілттерді есептеу алгоритмі. Осы алгоритм күрделенген сайын, соғұрлым шифрдің криптоанализі көп дәрежеде ұлғаяды.
Раунд функциясы. Бұл жерде де қиыншылықтар, ереже бойынша, криптоанализдің көзқарасы бойынша шифрдің қатаңдығының жоғарылануына әкеледі.

Сонымен қатар, Файстель шифрінің кез-келген реализациясын құруда керек болатын тағы да екі фактор бар.

Шифрлеу/дешифрлеу программаларының орындалу жылдамдығы. Шифрлеу функциялары шифрлеудің аппаратты реализациясының керек емес екендігін көрсету үшін қосымшалар мен утилиттерге қойылады. Мұндай жағдайда алгоритмнің программалық орындалу жылдамдығы маңызды фактор болып табылады.
Анализдің қарапайымдылығы. мүмкін болғанша криптоанализға барынша қиын етіп, бірақ осы алгоритм түсінуге қолайлы болатындай алгоритм құру біздің мақсатымыз болып табылады. Басқа сөзбен, егер алгоритм қолайлы және түсінікті болса, криптоанализға осал көзбен қарағанда оны анализдеу оңайға соғады, және сенімділіктің тым жоғарырақ дәрежеге жету мақсатында оңайырақ орындалады. Мысалы, DES алгоритмін анализ үшін өте қарапайым алгоритмдерге жатқызуға болмайды.

3. 1 және 3. 3 сур. қайта оралсақ, S-DES ақпаратты өңдеудің екі раундтты Файстель схемасын қолданатынын байқаймыз. Файстель схемасынан бір ерекшелік, ол S-DES алгоритмі перестановканың орындалуымен басталады да, аяқталады да. Осы ерекшелік жартылай функциональды DES алгоритмі үшін де қатысты.

Дешифрлеу алгоритмі

Файстель шифрын дешифрлеу процессі шифрлеу процесінен өзгешеленбейді. Сол алгоритмнің өзі қолданылады, бірақ кірісіне шифрленген текст беріледі, ал 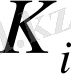құрамды кілттері кері ретпен қолданылады: бірінші раунды үшін 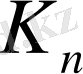құрамды кілті алынады, екіншісіне - 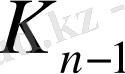және т. с. с.,

соңғы раундына 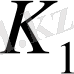кілті енгізілмегенше дейін. Берілген шифрлеу схемасының осы қасиеті өте ыңғайлы болып табылады, себебі дешифрлегенде шифрлеу алгоритмінен күшті екінші алгоритмді енгізу керек емес.