Термодинамика негіздері: молекуланың еркін дәрежелері, энергияның біркелкі бөлінуі, ішкі энергия және термодинамиканың I заңы


Тақырып: Термодинамика негіздері
1. Молекуланың еркін дәрежелер саны. Энергияның еркін дәрежелерге біркелкі бөліну заңы
Термодинамикалық жүйенің ең маңызды сипаттамаларының бірі ішкі энергия U болып табылады. Ол жүйедегі микробөлшектердің (молекула, атом, электрон, ядро, т. б. ) хаосты (жылулық) қозғалысының және осы бөлшектердің өзара әсерлесу энергиясы болып табылады. Біртұтас жүйенің қозғалысының кинетикалық энергиясы мен сыртқы өрістегі жүйенің потенциалдық энергиялары ішкі энергия болып есептелінбейді.
Ішкі энергия - жүйенің термодинамикалық күйінің функциясы, демек жүйенің әр күйде белгілі бір ішкі энергиясы болады. Жүйе бір күйден екінші бір күйге өткенде оның ішкі энергиясының өзгерісі сол күйлердің ішкі энергияларының айырмасымен анықталады:
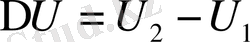 . Жүйенің ішкі энергиясының өзгерісі жүйе бір күйден екінші күйге қандай жолмен келгеніне тәуелсіз шама болып табылады.
. Жүйенің ішкі энергиясының өзгерісі жүйе бір күйден екінші күйге қандай жолмен келгеніне тәуелсіз шама болып табылады.
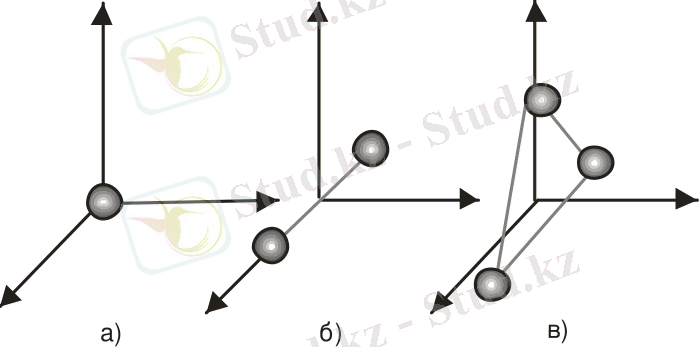
Еркін (еріктілік) дәрежелер саны деп жүйенің кеңістіктегі орнын толықтай анықтайтын тәуелсіз айнымалылар (координаталар) санын айтады. Мысалы, көптеген есептерде бір атомды газ молекуласын ілгерілемелі қозғалыстың үш еркін дәрежесі бар материялық нүкте ретінде қарастырады да, айналмалы қозғалыстың энергиясы ескерілмейді:
і
=
3. Сурет 11, а) жағдайы (

 ) .
) .
Сурет 11
Классикалық механикада екі атомды газдың молекуласын деформацияланбайтын, қатаң байланысқан екі материялық нүктелердің бірігуі ретінде қарастырады. Бұл жүйе ілгерілемелі қозғалыстың үш еркін дәрежесінен басқа айналмалы қозғалыстың екі еркін дәрежесіне де ие болады. Сурет 11, б) жағдайы. Себебі, жүйе екі ось бойымен айналады, ал екі атом арқылы өтетін үшінші осьтен айналудың мағынасы жоқ деп есептелінеді, демек, молекуласы екі атомнан тұратын газдың бес еркін дәрежелері бар: і = 5.
Үш атомды және көп атомды бейсызықты молекулалардың алты еркін дәрежелері бар: үшеуі ілгерілемелі және үшеуі айналмалы қозғалыстардікі деп есептелінеді, і = 6. Сурет 11, в) жағдайы.
Нақты газ молекулалары арасында қатаң байланыс жоқ, сондықтан нақты газ молекулалары үшін тербелмелі қозғалыстың да еркін дәрежелерін ескеру қажет. Жалпы санына байланыссыз молекуланың үш еркін дәрежесі әрқашанда ілгерілемелі қозғалыстікі. Ілгерілемелі қозғалыстың еркін дәрежелерінің бірінен бірінің артықшылығы жоқ, демек олардың әрқайсысына орташа есеппен
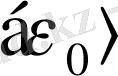 кинетикалық энергияның
кинетикалық энергияның
 бөлігіне тең энергия келеді:
бөлігіне тең энергия келеді:
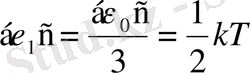 .
.
Классикалық статистикалық физикада энергияның еркін дәрежелеріне біркелкі бөліну заңын
Больцман
қорытып шығарды:
термодинамикалық тепе-теңдік күйдегі статистикалық жүйенің әрбір ілгерілемелі және айналмалы қозғалысының еркін дәрежелеріне орта есеппен
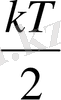 -ге тең кинетикалық энергия, ал тербелмелі қозғалыстың еркін дәрежесіне орта есеппен
-ге тең кинетикалық энергия, ал тербелмелі қозғалыстың еркін дәрежесіне орта есеппен
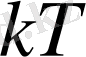 -ға тең кинетикалық энергия келеді.
Тербелмелі қозғалыстың еркін дәрежесіне екі есе көп энергия келу себебі, кинетикалық энергияға тең потенциялық энергия да ескеріледі. Молекуланың еркін дәрежелерін ескере отырып, орташа кинетикалық энергияның өрнегін жазуға болады:
-ға тең кинетикалық энергия келеді.
Тербелмелі қозғалыстың еркін дәрежесіне екі есе көп энергия келу себебі, кинетикалық энергияға тең потенциялық энергия да ескеріледі. Молекуланың еркін дәрежелерін ескере отырып, орташа кинетикалық энергияның өрнегін жазуға болады:
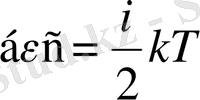 .
.
Мұндағы
і=
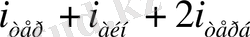 .
.
Идеал газ молекулалары өзара әсерлеспейді деп есептелінгендіктен молекулалар арасындағы өзара әсердің потенциялық энергиясы нульге тең. Демек,
газдың бір молінің ішкі энергиясы
 молекулалардың кинетикалық энергияларының қосындысына тең:
молекулалардың кинетикалық энергияларының қосындысына тең:
 , (1. 1)
, (1. 1)
m массалы газ үшін ішкі энергия өрнегін жазайық:
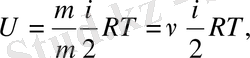
2. Термодинамиканың бірінші бастамасы (заңы) . Механикалық энергиясы өзгермей ішкі энергиясы ғана өзгеретін термодинамикалық жүйені қарастырайық. Жүйенің ішкі энергиясы түрлі процестер нәтижесінде өзгеруі мүмкін:
1) жұмыс жасау арқылы;
2) жылу беру (қыздыру) арқылы.
Мысалы, газы бар цилиндрдегі поршеньді ығыстыру арқылы біз газды сығамыз, нәтижесінде газдың температурасы көтеріледі, яғни ішкі энергиясы артады. Газға белгілі мөлшерде жылу беру арқылы да біз ішкі энергиясын өзгертуімізге болады. Демек, жылу мөлшері дегеніміз жүйенің сыртқы денелер арқылы жылу алмасу процесі кезінде энергиясының артуы (түрлі температурадағы денелердің жылу алмасуы немесе ішкі энергияларымен алмасуы) .
Механикалық қозғалыс энергиясы жылулық қозғалыстың энергиясына және керісінше ішкі энергия механикалық қозғалыс энергиясына айнала алады. Бұл айналуларда энергияның бір түрден екінші түрге айналу және сақталу заңы орындалады. Термодинамиканың 1 заңы термодинамикалық процестерге қатысты энергияның сақталу заңы болып табылады. Термодинамиканың 1 заңы көптеген тәжірибелердің нәтижесі.
Ішкі энергиясы
 -ге тең жүйе (поршені бар цилиндрдің ішіндегі газ)
Q
жылу мөлшерін алды да ішкі энергиясы
-ге тең жүйе (поршені бар цилиндрдің ішіндегі газ)
Q
жылу мөлшерін алды да ішкі энергиясы
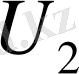 -ге тең жаңа күйге көшті делік, сонда жүйе сыртқы күштерге қарсы жұмыс жасады. Жүйеге берілетін жылу мөлшері және жүйе сыртқы күштерге қарсы жасайтын жұмыс оң шама болып есептелінеді. Тәжірибе көрсеткендей, энергияның сақталу заңы бойынша жүйе бір күйден екінші күйге қандай жолмен көшкеніне тәуелсіз ішкі энергияның өзгерісі
-ге тең жаңа күйге көшті делік, сонда жүйе сыртқы күштерге қарсы жұмыс жасады. Жүйеге берілетін жылу мөлшері және жүйе сыртқы күштерге қарсы жасайтын жұмыс оң шама болып есептелінеді. Тәжірибе көрсеткендей, энергияның сақталу заңы бойынша жүйе бір күйден екінші күйге қандай жолмен көшкеніне тәуелсіз ішкі энергияның өзгерісі
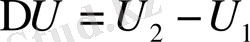 тең, демек жүйенің алатын жылу мөлшері
Q
мен сыртқы күштерге қарсы жасалатын жұмыстың
А
айырымына тең болады:
тең, демек жүйенің алатын жылу мөлшері
Q
мен сыртқы күштерге қарсы жасалатын жұмыстың
А
айырымына тең болады:
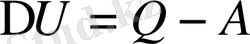 немесе
немесе
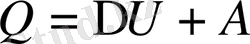 (1. 2)
(1. 2)
(1. 2) теңдеуі термодинамиканың 1 заңының өрнегі болып табылады: жүйеге берілетін жылу мөлшері оның ішкі энергиясын өзгертуге және сыртқы күштерге қарсы жұмыс жасауға жұмсалады. (1. 2) теңдеуін дифференциалдап келесі өрнекті аламыз:
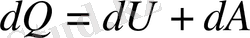 немесе
немесе
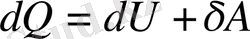 . (1. 3)
. (1. 3)
Мұндағы
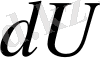 - жүйенің ішкі энергиясының
- жүйенің ішкі энергиясының
 кіші өзгерісі,
кіші өзгерісі,
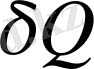 -
-
 кіші жылу мөлшері,
кіші жылу мөлшері,
 - элементар жұмыс.
- элементар жұмыс.
(1. 2) өрнегінен ХБЖ жылу мөлшері энергия және жұмыстың өлшем бірлігі болып табылатын Джоульмен (Дж) өлшенетінін көреміз.
Егер жүйе процесс аяғында өзінің бастапқы күйіне қайта оралатын болса, онда ішкі энергияның өзгерісі нольге тең болады:
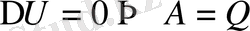 .
.
Демек, термодинамиканың бірінші заңы бойынша сырттан берілетін энергиядан артық жұмыс жасайтын машина жасау мүмкін емес, яғни мәңгі двигательдің 1-ші түрін жасау мүмкін емес (термодинамиканың 1 заңының тағы бір тұжырымдамасы) .
3. Газдың көлемі өзгергендегі жұмысы.
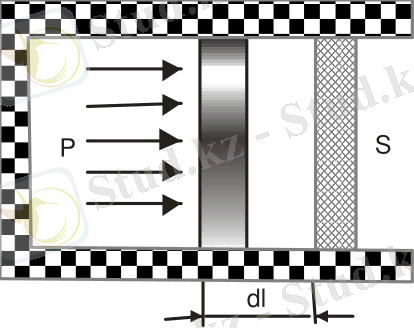
Көлемі өзгергендегі газдың сыртқы күштерге қарсы жұмысын табу үшін нақты процесті қарастырайық. Мысалы, газ толтырылған поршені бар цилиндрді алайық, сурет 12.
Сурет 12
Цилиндр мен поршень арасындағы газ көлемі ұлғайғанда поршеньді
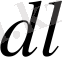 - шексіз кіші арақашықтыққа жылжытады, сонда газдың сыртқы күштерге қарсы жасайтын жұмысы мынаған тең:
- шексіз кіші арақашықтыққа жылжытады, сонда газдың сыртқы күштерге қарсы жасайтын жұмысы мынаған тең:
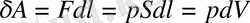 .
.
Мұндағы
 - поршеньнің ауданы,
- поршеньнің ауданы,
 - жүйенің көлемінің өзгерісі. Демек,
- жүйенің көлемінің өзгерісі. Демек,
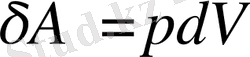 (1. 4)
(1. 4)
Көлемі
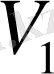 -ден
-ден
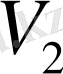 -ге дейін өзгергенде газдың жасайтын толық жұмысын (1. 4) теңдеуін интегралдап табамыз:
-ге дейін өзгергенде газдың жасайтын толық жұмысын (1. 4) теңдеуін интегралдап табамыз:
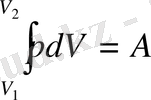 .
.
4. Идеал газдың жылусыйымдылығы.
Меншікті жылу сыйымдылығы деп 1кг затты 1К температураға дейін қыздыру үшін қажетті жылу мөлшерін айтады.
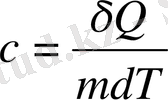 . (1. 5)
. (1. 5)
Меншікті жылу сыйымдылығының өлшем бірлігі - Дж/ кгК.
Молярлық жылусыйымдылығы деп 1 моль затты 1 К температураға дейін қыздыруға қажетті жылу мөлшерін айтады.
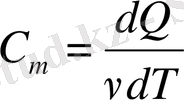 ; (1. 6)
; (1. 6)
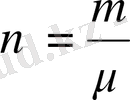 - зат мөлшері, ол мольдер санын анықтайды.
- зат мөлшері, ол мольдер санын анықтайды.
Меншікті және молярлық жылу-сыйымдылықтарының арасындағы байланысты көрсететін өрнек:
 , (1. 7)
, (1. 7)
мұндағы
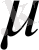 - молярлық масса.
- молярлық масса.
Тұрақты көлемде немесе тұрақты қысымда қыздырылған зат үшін жылусыйымдылықтарын қарастырайықққ. Термодинамиканың 1 заңын 1 моль газ үшін жазайық.
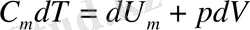 . (1. 8)
. (1. 8)
Егер газ тұрақты көлемде қыздырылса, онда жұмыс нульге тең, сондықтан сырттан берілетін жылу мөлшері оның ішкі энергиясының көбеюіне жұмсалады:
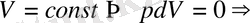
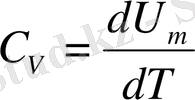 . (1. 9)
. (1. 9)
Демек, тұрақты көлемдегі молярлық жылусыйымдылық 1 моль газды 1 К температураға дейін қыздырғандағы ішкі энергияның өзгерісіне тең .
Ішкі энергия
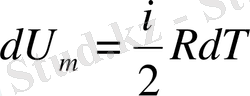 екенін ескере отырып, тұрақты көлемдегі жылусыйымдылықтың өрнегін жазайық:
екенін ескере отырып, тұрақты көлемдегі жылусыйымдылықтың өрнегін жазайық:
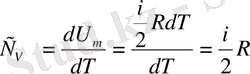 . (1. 10)
. (1. 10)
Егер газ тұрақты қысымда қыздырылса, термодинамиканың 1 заңын пайдаланып, тұрақты қысымдағы жылусыйымдылықты табуға болады.
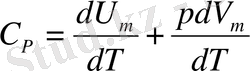 .
.
Ішкі энергия қысымға да, көлемге де тәуелді емес, тек температураға тәуелді екенін және
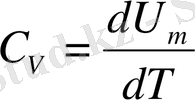 ескере отырып және Менделеев - Клапейрон теңдеуін дифференциалдап, тұрақты қысымдағы молярлық жылусыйымдылықты табамыз:
ескере отырып және Менделеев - Клапейрон теңдеуін дифференциалдап, тұрақты қысымдағы молярлық жылусыйымдылықты табамыз:

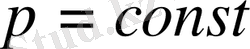 ,
,
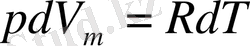
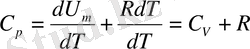 .
.
 (1. 11) өрнегі
Майер теңдеуі
деп аталады.
(1. 11) өрнегі
Майер теңдеуі
деп аталады.
Бұл теңдеу тұрақты қысымдағы молярлық жылусыйымдылықтың тұрақты көлемдегі молярлық жылусыйымдылықтан универсал газ тұрақтысының шамасына артық екенін көрсетеді. Ол тұрақты қысымда газды қыздыру үшін газды ұлғайтуға қосымша жылу мөлшері керектігімен түсіндіріледі, себебі қысымды тұрақты ету үшін көлемді ұлғайту қажет.
Тұрақты көлемдегі молярлық жылусыйымдылықтың өрнегін пайдаланып, тұрақты қысымдағы молярлық жылусыйымдылықтың еркін дәреже санына тәуелділігін аламыз:
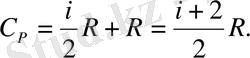 (1. 12)
(1. 12)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz