Төрт полюстіктер: негізгі теңдеулер мен пассивті формалар

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

1. Төрт полюстіктер және олардың негізгі теңдеулері

Электр тізбектерінің анализ жасағанда, кез келген екі тармақтардың айнымалы шамаларының (тоқ, кернеу, қуат) байланысын зерттейтін есептерде төртполюстіктер теориясы кеңінен қолданады.

Төрт полюстіктер- бұл конфигуациясы әр түрлі, екі пара қысқыштары (полюстері) бар схеманың бөлігін атайды. Қысқыштарды кіріс және шығыс деп екіге бөледі. Төрт полюстіктеге мысалы трансформатор, күшейткіш(усилитель), потенциометр, электр желісі және екі пара полюсын бөліп көрсетуге болатын электротехникалық құрылғылар жатады. Жалпы алғанда, төртполюстіктерді активті және пассивті деп екіге бөледі. Активты төртполстіктерд өз құрамында энергия көздері болады, ал пассивті төртполюстіктерде энергия көзі болмайды. Бұл дәрісте теориясы қарастырылады. Төрт полюстіктің теңдеуін жазу үшін кез келген схемадан жалғыз энергия көзі бар тармақты

және кез келген кедергісі бар тармақты бөліп аламыз. (сур. 1, а) .

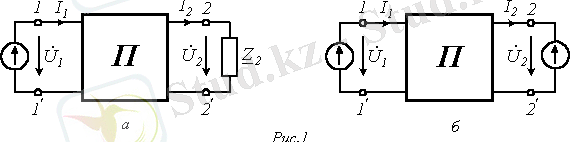
Сурет - 1

Компенсация принциін қолданып берілген кедергісін кернеуі 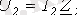(сур. 1, б) кернеу көзіне орын ауыстырамыз. Сонда, қабаттасу әдісі бойынша 1, б суретіндегі тізбек үшін келесі теңдеу жазамыз:

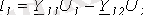; (1)

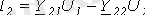. (2)

(1) және (2) теңдеулерін бірінші қысқыштардағы кернеу мен тоққа қатысты шығарып, келесіні табамыз

;

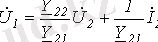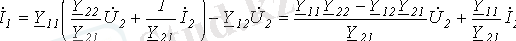
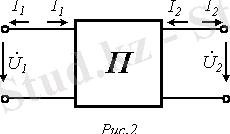
image033-4

Сурет -2

немесе

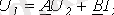; (3)

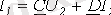, (4)

мұнда ; ; 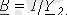; 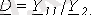- төрт полюстіктің коэффициенттері. Өзаралық принцип бойынша 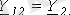, көріп отырғандай төрт полюстіктің коэффициенттеріөзара келесі қатынаспен байланысқан:

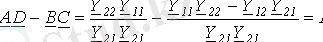(5)

(3) және (4) теңдеулерін төрт полюстіктің в А-формасындағы теңдеулері деп атайды. (табл. 1) . Әр түрлі формадағы теңдеулер үшін тоқтардың оң бағыты 2 ші суреттегідей алынған.

2. Пассивті төрт полюстіктің теңдеулерінің формалары

Егер, энергия көзі мен қабылдағыштың орнын ауыстырғанда олардың тоқтары өзгермесе, ондай төрт полюстікті симметриялы деп атайды. Бұл келесі жағдайда орындалады: 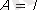. Бұл шартқа сәйкес келмейтін төртполюстіктер бейсимметриялы деп аталады

Форма

теңдеулер

Негізгі теңдеулердің коэффициентерімен байланыс

Форма: А-форма

теңдеулер:

;

Негізгі теңдеулердің коэффициентерімен байланыс:

Форма: Y-форма

теңдеулер:

;

Негізгі теңдеулердің коэффициентерімен байланыс:

;

Форма: Z-форма

теңдеулер:

;

Негізгі теңдеулердің коэффициентерімен байланыс:

;

Форма: Н-форма

теңдеулер:

;

Негізгі теңдеулердің коэффициентерімен байланыс:

;

Форма: G-форма

теңдеулер:

;

Негізгі теңдеулердің коэффициентерімен байланыс:

;

Форма: B-форма

теңдеулер:

;

Негізгі теңдеулердің коэффициентерімен байланыс:

;

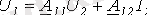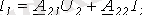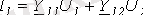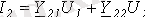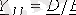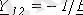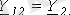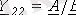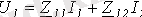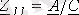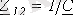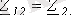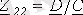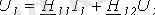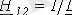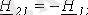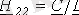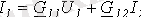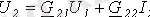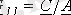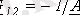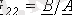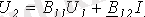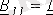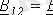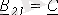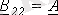Таблица 1. Пассивті төрт полюстіктің теңдеулерінің формалары

Практикада тізбектерді анализ жасауға қолданғанда төртполюстіктің коэффициенттерінің мәні белгілі болу керек. Оларды эксперименталды немесе есептеу арқылы анықтауға болады. (5) теңдеу бойынша егер үш коэффициент анықталса онда төртіншісін де анықтауға болады. Ең қолайлы эксперименталды әдістердің бірі бос жүріс және қысқа тұйықтау тәжірибелеріне негізделген. Ол үшін бос жүріс тәжірибесінде бірінші қысқыштар жағынан қоректену, қысқа тұйықтау тәжірибесінде екінші қысқыштар жағынан қоректену. Бұлжағдайда, болғанда (3) және (4) теңдеулер негізінде

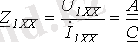. (6)

$H:\для ЦДО 2011-12 СДАННЫЕ\Из Интернента\Пассивные четырехполюсники_ (Лекция N 14).files\image112-9.gif$ болғанда

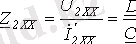(7)

Және 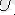болғанда

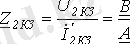(8)

(6) -(8) теңдеулерін төртполюстіктің коэффициенттеріне қатысты шешкенде:

Төртполюстіктің коэффициенттерін есептеу арқылы анықтау үшін оның схемасы және кедергілерінің мәндері белгілі болуы керек.

Пассив төртполюстікті үшэлементті эквивалентті Т- тәрізді схема (сур. 3, а) немесе П-тәрізді (сур. 3, б) орынбасу схемасымен көрсетуге болады.

3, а суретіндегі төртполюстіктің коэффициенттерін анықтау үшін Кирхгоф заңарын қолданып 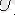кернеуін 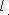тоғы арқылы, кернеуін 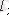арқылы жазамыз:

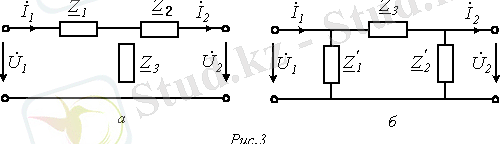
Сурет -3

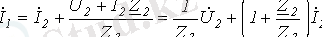(9)

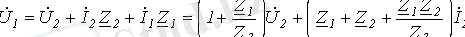(10)

(9) және (10) теңдеулерін (3) және (4) теңдеулерімен қарастырғанда келесі формулаларды береді:

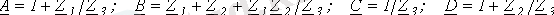
Бүл есепті басқа жолмен шығаруға болады

болғанда (бос жүріс екінші қысқыштар жағынан) (3) және (4) теңдеулері бойынша

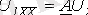және ;

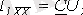Бірақ 3, а суретіндегі схемадан

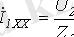, а ;

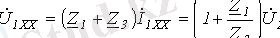Одан келесі шығады: және .

болғанда (қысқа тұйықтау екінші қысқыштар жағында)

және .

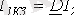6. 3, а суретіндегі схемадан

; .

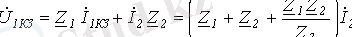Яғни, .

Сонымен бірінші есептегендей қорытынды шықты

6. 3, б суретіндегі төртполюстіктің коэффициенттерін аналогия бойынша тап осы жолмен есептеуге болады немесе 6. 3, а суретіндегі схеманың табылған шешімдері бойынша «жұлдызша-үшбұрыш» түрлендіруін қолданып табуға болады.

Жоғарыда айтылғаннан келесі қорытынды шығаруға болады: төртполюстіктің коэффициенттері белгілі болса, Т- және П- тәрізді орынбасу схемаларының параметрлерін табуға болады.

Практикада теңдеулер жазудың бір формасынан екіншіформаға өту қажеттігі көп кездеседі. Бұл есепті шығару үшін, бір форманың коэффициенттері арқылы екінші форманың коэффициентерін табу үшін, осы формулалардағы екі бірдей шаманы қалған екеуі арқылы тауып, әр формадағы тоқтың оң бағытын ескере отырып, қарастыру керек. Мысалы, А - формадан Z-формаға өткенде (4) теңдеу негізінде:

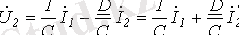(11)

(11) теңдеуін (3) теңдеуге қойып табамыз:

(12)

(11) және (12) теңдеулерін Z-формадағы ( табл. 1) теңдеулермен салыстырып, табамыз

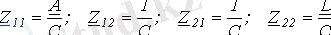Төртполюстіктің 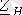жүктемеге жұмысын анализ жасағанда бірінші қысқыштар жағынан кіріс кедергісі 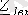түсінігін және тасымал коэффициентін 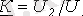қолданған ыңғайлы. Келесі

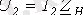және ескере отырып, осы параметрлер үшін келесіні жазуға болады:

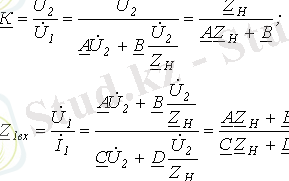
Кіріспе

Кез келген екі тармақтардың айнымалы шамаларының (тоқ, кернеу, қуат) байланысын зерттейтін есептерде төртполюстіктер теориясы кеңінен қолданады. Электр тогы энергетика саласында - энергияны алыс қашықтыққа жеткізу үшін, ал телекоммуникация саласында - ақпаратты шалғайға тасымалдау үшін қолданылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.