Алгебралық есептерді шешуде геометриялық әдісті пайдалану

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Мазмұны
Кіріспе
Негізгі бөлім
1. Вектор ұғымының теориялық сипатталуы
1.1. Вектор ұғымы және оның шығу тарихы
1.2. Векторларға амалдар қолдану
2. Алгебралық есептерді шешуде геометриялық әдісті пайдалану
2.1. Негізгі теориялық материалдарды еске түсірейік
Қорытынды
Пайдаланылған әдебиеттер тізімі

Кіріспе

Жұмыстың өзектілігі: Вектор ұғымы енгізіліп, оларға қолданылатын амалдар (қосу,азайту, санға көбейту, скалярлық көбейту) Векторға байланысты қозғалыс, күш, жылдамдық, электр тогы, токтың магнит өрісінің магниттік сызықтары ,жарық сәулесінің бағыты түсініктерін қалыптастыру арқылы пәнаралық байланыс нығая түседі.
Мақсаты: Математика курсында оқытылатын векторлар ұғымының шығу тарихына шолу жасау , векторлар ұғымы туралы негізгі түсініктердің мәнін ашу, вектордың түрлеріне тоқталу, векторларға қолданылатын негізгі амалдарды көрсету,векторларға амалдар қолдана білу дағдысын қалыптастыру
Міндеті: Векторлардың координаталарын қарастырғанда , векторлық алгебраның элементтерімен таныстыру, вектордың координаталарын басы мен ұшының координаталары арқылы табуда , вектордың абсолют шамасын ( ұзындығын ) есептегенде, векторлардың коллинеарлығын зерттегенде векторды санға көбейткенде , векторлардың скалярлық көбейтіндісін тапқанда алгебрадағы арифметикалық амалдарды қолданады
Жаңалығы: оқушылардың барлығы дерлік векторларға геометриялық (үшбұрыш, параллелограмм әдістері) және координаталық жолмен амал қолдана білсе, сонымен қатар, стандартты ойлауды логикалық ойлаумен ұштастыра алуда сыныптастарыма ықпал етсем деймін
Әдіс - тәсілі: баяндау
Жұмыс құрылымы кіріспе,негізгі бөлім,тараушалардан , қорытынды және пайдаланылған әдебиеттер тізімінен тұрады

Негізгі бөлім
1. Вектор ұғымының теориялық сипатталуы
1.1 Вектор ұғымы және оның шығу тарихы

Ғылым мен техникада кездесетін кейбір шамалар тек сан мәнімен ғана сипатталады (абсолют шамасымен) .Мысалы, ұзындық, аудан, көлем, масса, уақыт, температура энергия және т.б. жатады. Бұл шамаларды скаляр шамалар деп атайды. Ал, кейбір шамалар сан мәнімен ғана емес , сонымен қатар бағытымен де сипатталады.Мысалы: жылдамдық , үдеу, күш, импульс және т.б. Бұл-векторлық шамалар .
Қоғамдағы қазіргі кездегі қайта құрулар, экономиканы дамытудағы жаңа стратегиялық жоспарлар,әлемнің жетекші елдерінің көпшілігі білім берудегі мақсатты көздейді. Жас ұрпақты жан-жақты жетілген,ақыл-парасаты, өресі биік етіп тәрбиелеу. Математиканы оқытудағы негізгі міндет - математикалық білім, білік жүйелерін қалыптастыру. Тәуелсіз Қазақстанымыздың экономикасы өркендеп, өндіріс орындарыныың жандануына байланысты математика пәнінің ролі ерекше зор
Елімізге қажет болып отырған мамандарды бүгінгі күні мектеп партасынан бейімдеуіміз қажет. Біздің жоғары оқу орындарымыздың физика-математика және техника салалары бойынша бұл тұрғыда оқушыларға мектепте оқытылатын математика салаларында тақырыпты меңгеруде көптеген
қиындықтар кездеседі.
Мектеп математика курсында векторлар тақырыбына 15 сағат берілген
Техника ғылымдардың қауырт дамуына байланысты он сегізінші ғасырдың өзінде-ақ векторлық есептеулерді жасауға көптеген елдердің ғалымдары атсалысты. Аристотельдің қозғалыстарды (орын ауыстыруларды) қосуға параллелограмм ережесін қолданғандығы - векторлардың геометриялық қосындысын табу біздің заманымызға дейін жетті. Он жетінші ғасырда Аристотельдің "қозғалыстар параллелограмы" қайтадан жанданды.
Механикадағы векторлық алгебраның негізін қалаушы Джон Валлис (1616-1703) механикаға өз үлесін қосты. Он сегізінші ғасырда математика мен механикада аналитикалық әдістерімен әуестену басым. Множ-Понселе мектебінің көрнекті өкілі Баре де Сен-Венан (1797-1886) серпімділік, Понселенің шәкірті Резаль (1820-1896) 1862-жылы жарияланған "Чистая кинематика" еңбегі , векторлық есептеулердің негізін салушылар Ирландия математигі әрі астрономы Уильям Гамильтонның 1844-жылы векторлық есептеулерге арналған алғашқы мақалалары жарық көрді.
Есептеудің жаңа түрі бойынша 1918 жылы танымал математик Герман Вейль (1885-1955) векторлық аксиоматиканы векторлық есептеулерді жасауға үлес қосқандардың ең алғашқылары болып табылады.

1.2. Векторларға амалдар қолдану
Векторларды анықтау. Векторды базис бойынша жіктеу
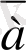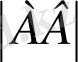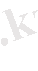
Анықтама. Вектор деп бағытталған кесіндіні атайды да, = символмен белгілейді. ара қашықтығы векторының ұзындығы деп аталады. Еркін векторлар жиыны мен олардың кеңістікті параллель жылжыту жиыны арасындағы изоморфизмды ескерсе, егерде қосу операциясын жылжыту композицияларымен теңестірсе, онда кеңістікті параллель жылжыту жиынын тіпті векторды анықтау үшін де пайдалануғы болады.
Кеңістікті шексіз аз трансформацияларын зерттеуде маңызды рөл атқарады.
* Бaс нүктесі соңғы нүктесімен беттесетін векторды нөль-вектор деп атайды:
* векторын векторына қарсы вектор деп атайды.
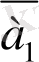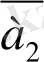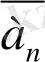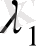
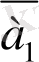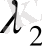
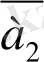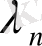
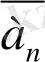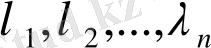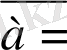
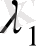
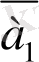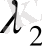
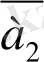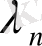
Анықтама. , ,..., векторларының сызыктык комбинациясы деп мына түрдегі + +...+ кез келген векторды атайды, мұндағы нақты сандарын сызықтық комбинацияның коэффициенттері деп атайды. Егер + +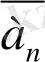...+ болса, онда 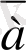векторы 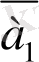, ,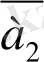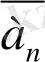..., векторлары бойынша жіктелген дейді.
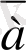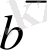Анықтама. Бағыттары бірдей немесе қарама - қарсы бағытталған нөлдік емес және векторлары коллинеар векторлар деп аталады да арқылы белгілінеді. Жазықтықтағы базис деп белгілі бір ретпен алынған осы жазақтықтың кез келген коллинеар емес векторлар парын атайды.
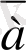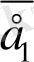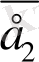Теорема. Жазықтағы кез келген векторын осы жазықтықтың коллинеар емес кез келген және векторлары бойынша жіктеуге болады және ол жіктеу жалғыз ғана болады, яғни 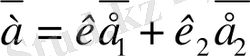. К1, к2 сандары 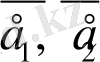базісі бойынша алынған 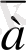векторының координаталары деп аталады да, алынған ретімен жақшаға алынып, былай 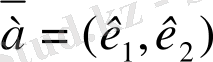жазылады.
Анықтама. Егер 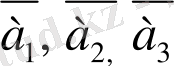векторлары бір жызыктыққа параллель болса, онда оларды компланар векторлар деп атайды.
Егер 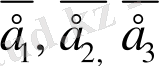компланар болса, онда 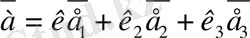жіктелу орындалады.
Өзінің сандық мәнімен қоса кеңістіктегі бағытымен де сипатталатын шамалар векторлық шамалар немесе векторлар деп аталады. Сонымен, орын ауыстыру векторлық шама болып табылады. Векторларды бағытталған кесінді түрінде кескіндейді және бір әріппен немесе вектордың басы мен ұшын көрсететін екі әріппен белгілеп, төбесіне нұскама (стрелка) қояды. Мысалы жылдамдық векторын ʋ немесе АВ, күш векторын F
немесе CD түрінде кескіндеуге болады. Кеңістікте белгілі бір бағыты болмайтын, тек сандық мәнімен ғана сипатталатын шаталар скалярлық шамалар немесе скалярлар деп аталады. Мысалы, уақыт, заттың тығыздығы, дененің көлемі, температура, арақашықтығын (орын ауыстыру емес), сынып бөлмесінің ұзындығы, ені және биіктігі, т.с.с. скалярлық шамаларға жатады.
Кез келген вектордың сандық мәні оның модулі деп аталады.Модуль -- скалярлық шама.Егер a және b векторларының модульдер і мен бағыттары
бірдей болса, онда олар тең болады а = b. Ал векторлардың модульдері тең болып, бірақ бағыттары қарама-қарсы болса, онда а = - b болады.

Векторларды қосу

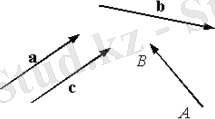
(1-сурет) Векторлар
Мысалы, кез келген а және b векторлары берілсін. Осы векторларды қосып, a + b-ға тең болатын с векторын табу керек. Ол үшін векторды өзіне-өзін параллель көшіргенде вектор өзгермейді дейтін ережені пайдаланамыз. Осы ереженің көмегімен векторларды қосудың бірнеше тәсілдерін көрсетуге болады. Мысалы, екі векторды бастарын түйістіре параллелограмның екі қабырғасы болатындай етіп өз-өзіне параллель көшіреміз де, параллелограмм саламыз. Сонда екі вектордың шыққан нүктесінен жургізілген бағыты көрсетілген диагональ қорытқы вектор болып табылады . Векторларды осылайша қосу параллелограмм ережесі бойынша қосу деп аталады.
Векторларды қосуда үшбұрыш ережесін де қолдануға болады. Ол үшін берілген векторларды бірінші вектордың ұшы екінші вектордың басымен түйісетіндей етіп, өз-өзіне параллель көшіреміз. Сонда бірінші вектордың басынан екінші вектордің ұшына қарай жүргізілген вектор сол екі вектордың қосындысын береді.
Ал енді екеу емес, бірнеше векторды қосу керек болса. Онда векторларды, алдыңғы вектордың ұшына келесі вектордың басы жалғасатындай етіп, әркайсысын параллель көшіреміз. Сонда алынған көпбұрыштың басы мен ұшын тұйықтап тұрған R векторы қорытқы вектор болып есептеледі. Ол бірінші вектордың басынан соңғы вектордың ұшына қарай бағытталады және мынаған тең болады: R = Ғ1+Ғ2+Ғ3 + Ғ4.

Векторларды азайту
Векторларды косу ережесінен векторларды азайту ережесін шығарып алуға болады. Мысалы, с = а - b векторын табу керек болсын. Бұл теңдікті с = a + ( - b) түрінде жазуға болады, яғни векторлардың айырымын табу үшін а азайғыш векторға модулі азайткыш векторға тең, бірақ оған карама-карсы бағытталған - b векторын қосу керек. Немесе екі векторды өздеріне параллель көшіріп, бастары бір нүктеден шығатындай етіп орналастырамыз. Содан соң олардың ұштарын азайтқыштан (b) азайғышка (a ) қарай бағытталған вектормен қосамыз. Міне, осы с векторы қорытқы вектор болады. Бір тузудің бойында жатқан немесе бір-біріне параллель Бір түзудің бойында жатқан немесе бір-біріне параллель векторлар бір жаққа қарай не қарама-қарсы бағытталуы мүмкін.
Мұндай векторлар а және b векторлары сияқты қосылады, яғни бірінші вектордың ұшы екінші вектордың басымен қосылады. Қорытқы вектор модулі бойынша қосылатын векторлар модульдерінің арифметикалық
қосындысына немесе арифметикалық айырымына тең. Қорытқы вектор қосылатын векторлармен бағыттас модулі үлкен вектор жаққа қарай бағытталады.

Векторларды скалярға көбейту (бөлу)
Берілген а векторын кез келген k скалярға көбейту (бөлу) үшін осы вектордың модулін берілген санға көбейтеміз (бөлеміз): b = k :: a (b = a :k). Қорытқы b вектордың бағыты k көбейткішінің (бөлгішінің) таңбасымен анықталады. Егер k оң болса (k 0), онда b векторы а векторымен бағыттас, ал k теріс болса (k 0), b векторының бағыты а векторының бағытына қарама-қарсы болады.
Үшбұрыш ережесі. Екі {\displaystyle {\vec {u}}} мен {\displaystyle {\vec {v}}} векторларын үшбұрыш ережесімен қосу үшін осы екі векторды өздеріне біреуінің бас жағы екіншісінің аяғымен беттесетіндей параллель көшіру керек. Сонда пайда болған үшбұрыштың үшінші қабырғасы бас жағы алғашқы вектордың басымен беттесетін бастапқы екі вектордың қосынды векторы болып табылады.
Параллелограмм ережесі Екі {\displaystyle {\vec {u}}} мен {\displaystyle {\vec {v}}} векторларын параллелограмм ережесімен қосу үшін екеуін
де бастары беттесетіндей параллель көшіріп параллелограммға болықтырады. Сонда екеуінің қосындысы деп параллелограммның осы екі вектор бас жағынан шығатын диагоналін айтады. Екі сырғанақ векторларды қосу тек қана олар жатқан екі түзу қиылысқанда ғана анықталған. Бұл жағдайда әр вектор өз түзуі бойымен қиылысу нүктесіне дейін көшіріліп, содан кейін параллелограмм ережесімен қосылады. Екі тұрақты векторларды қосу тек егер олардың ортақ бас нүктесі болғанда ғана анықталған. Бұл жағдайда да олар параллелограмм ережесімен қосылады.
Екі вектордың скаляр көбейтіндісі
Анықтама. Екі вектордың скаляр көбейтіндісі деп сол векторлардың модульдерін олардың арасындағы бұрыштың косинусына көбейтіндісін айтады, оны былайша белгілейді: ()= , мұндағы және векторларының арасындағы бурыш.
Егер және векторлары берілсін дейік, онда олардың скаляр көбейтіндісі мына формуламен есептеледі
()=
Салдар: Егер болса , онда вектор ұзындығы мына формула бойынша анықталады

Салдар. Егер және , онда және векторлары арасындағы бұрыш мына формула бойынша есептеледі:
cos
Салдар: векторының бағыттауыш косинустары
cos, cos, cos
Векторлардың скаляр көбейтіндісінің қасиеттері:
1. -- коммутативтілік.
2. -- дистрибутивтілік.
3. -- санға көбейтуге қатысты сызықтық қасиеті.
4. -- вектор нормасы.

Екі вектордың векторлық көбейтіндісі
Анықтама. және векторларының векторлық көбейтіндісі деп с= символымен белгіленген мына шартты қанағаттындыратын векторын атайды:
= Sпар.
және
с== ()
Векторларды аралас көбейтіндісі
Анықтама. векторларының аралас көбейтіндісі деп вектормен векторының скалярлық көбейтіндісіне тең санды атайды, яғни ()=().
1. Егер , , , онда олардың аралас көбейтіндісі үшінші ретті анықтауышқа тең, яғни
()=
2. векторлары компланар векторлар болуы үшін, олардың аралас көбейтіндісі нөлге тең болуы қажетті жуне жеткілікті, яғни ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.